Procesos estocásticos#
Un proceso estocástico es un fenómeno que evoluciona en el tiempo de acuerdo con leyes probabilísticas. En términos simples, es como si tuviéramos una “historia escrita por el azar”, donde cada valor futuro depende de cierta forma del pasado y de un componente aleatorio.
Un ejemplo importante en finanzas y economía es el random walk o camino aleatorio, que explica por qué los precios de activos (como acciones) parecen seguir trayectorias impredecibles.
Random Walk
Un random walk es un proceso en el que, en cada paso, hay la misma probabilidad de subir o bajar por un número aleatorio.
En un random walk el valor presente \(y_t\) depende de:
El valor en el tiempo anterior \(y_{t-1}\)
Una constante \(C\)
Un número aleatorio \(\varepsilon_t\), llamado ruido blanco
El ruido blanco es simplemente un número tomado de una distribución normal con media 0 y varianza 1.
La ecuación general de un random walk es:
Si \(C \neq 0\), se denomina random walk con drift (con tendencia).
Simulación paso a paso
Para entenderlo mejor, supongamos que \(C = 0\). Entonces:
Si partimos de un valor inicial \(y_0 = 0\):
- En \(t=1\):\[y_1 = y_0 + \varepsilon_1 = \varepsilon_1\]
- En \(t=2\):\[y_2 = y_1 + \varepsilon_2 = \varepsilon_1 + \varepsilon_2\]
- En \(t=3\):\[y_3 = y_2 + \varepsilon_3 = \varepsilon_1 + \varepsilon_2 + \varepsilon_3\]
En general, el valor en el tiempo \(t\) es la suma acumulada de los choques aleatorios:
Analogía del borracho saliendo de un bar
Imagina a una persona que sale de un bar después de haber bebido demasiado.
En cada paso que da:
Puede moverse un metro a la izquierda o un metro a la derecha.
La decisión es completamente aleatoria, como lanzar una moneda.
No podemos anticipar con certeza dónde estará después de varios pasos.
Si seguimos su trayectoria, veremos que algunas veces se aleja mucho hacia un lado, otras veces regresa hacia el centro, e incluso puede parecer que avanza en línea recta durante un rato. Sin embargo, todo esto ocurre únicamente por azar.
Relación con el random walk
En esta analogía:
La posición actual del borracho corresponde a \(y_t\).
La posición anterior es \(y_{t-1}\).
El paso aleatorio hacia la izquierda o derecha es el choque \(\varepsilon_t\).
La ecuación que lo representa es:
Ideas clave
Cada paso depende del anterior.
La trayectoria es impredecible, ya que \(\varepsilon_t\) es un número aleatorio.
Aunque el movimiento es aleatorio, pueden aparecer períodos largos en un solo sentido, lo que genera la ilusión de una tendencia.
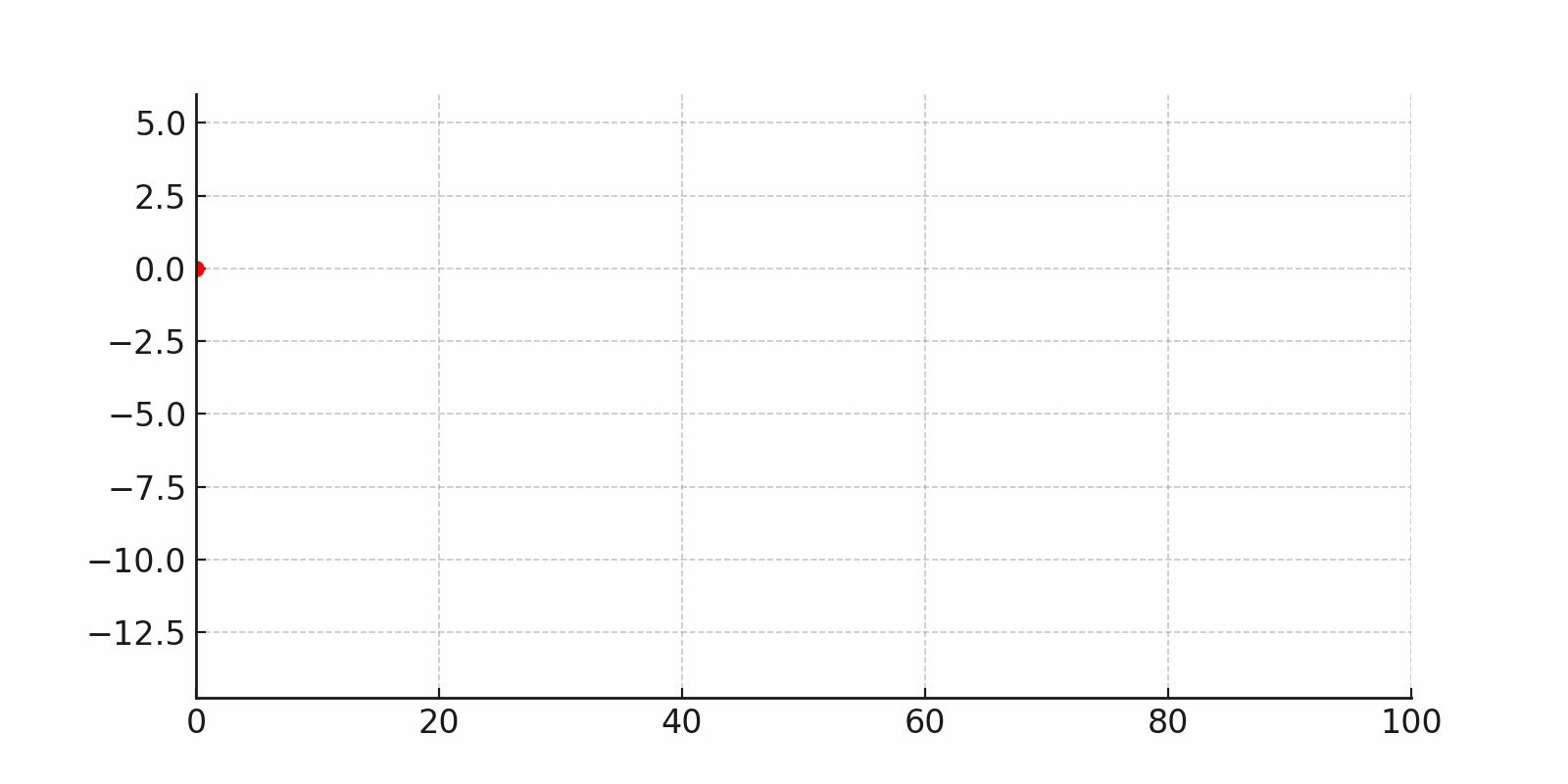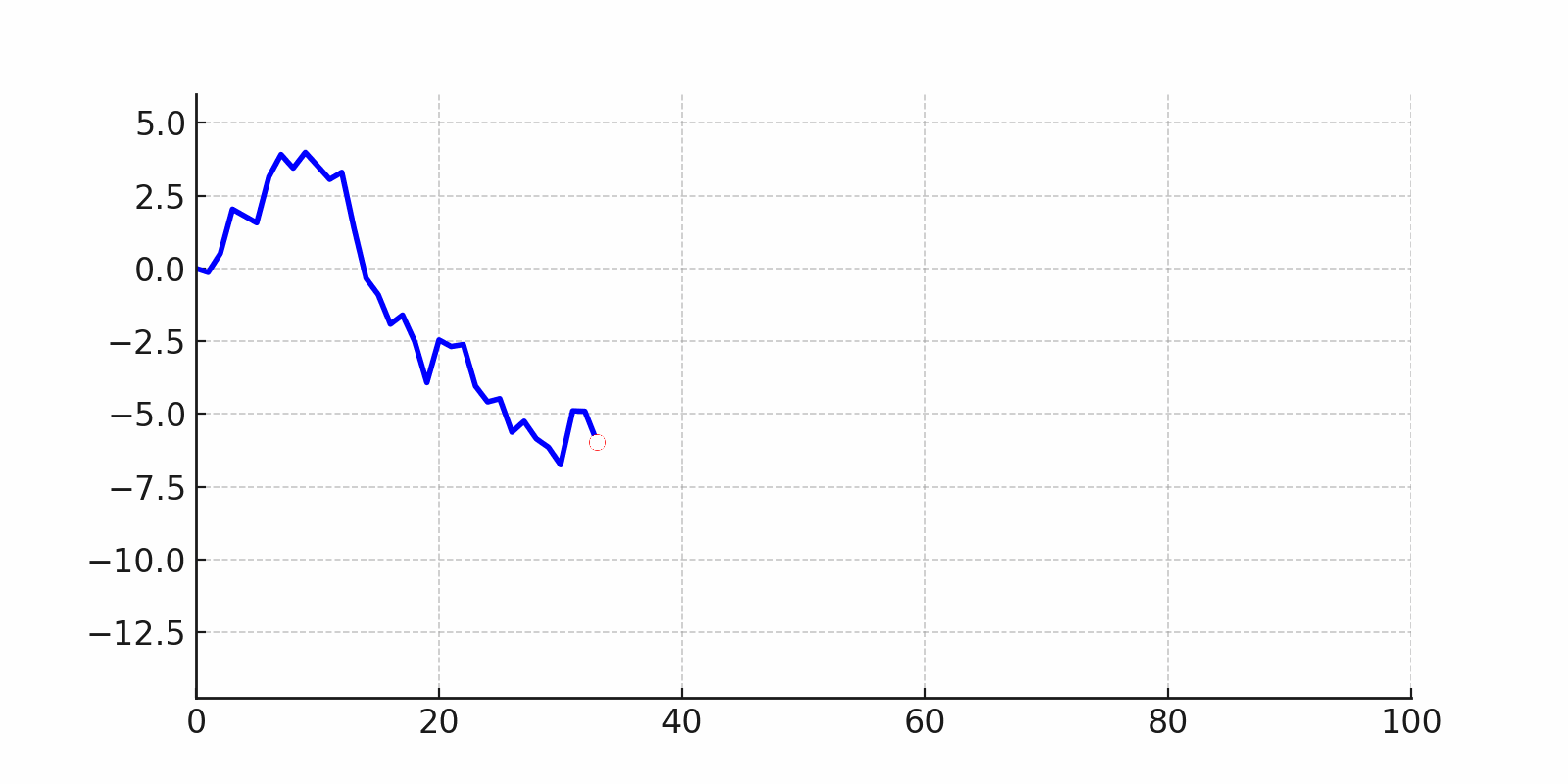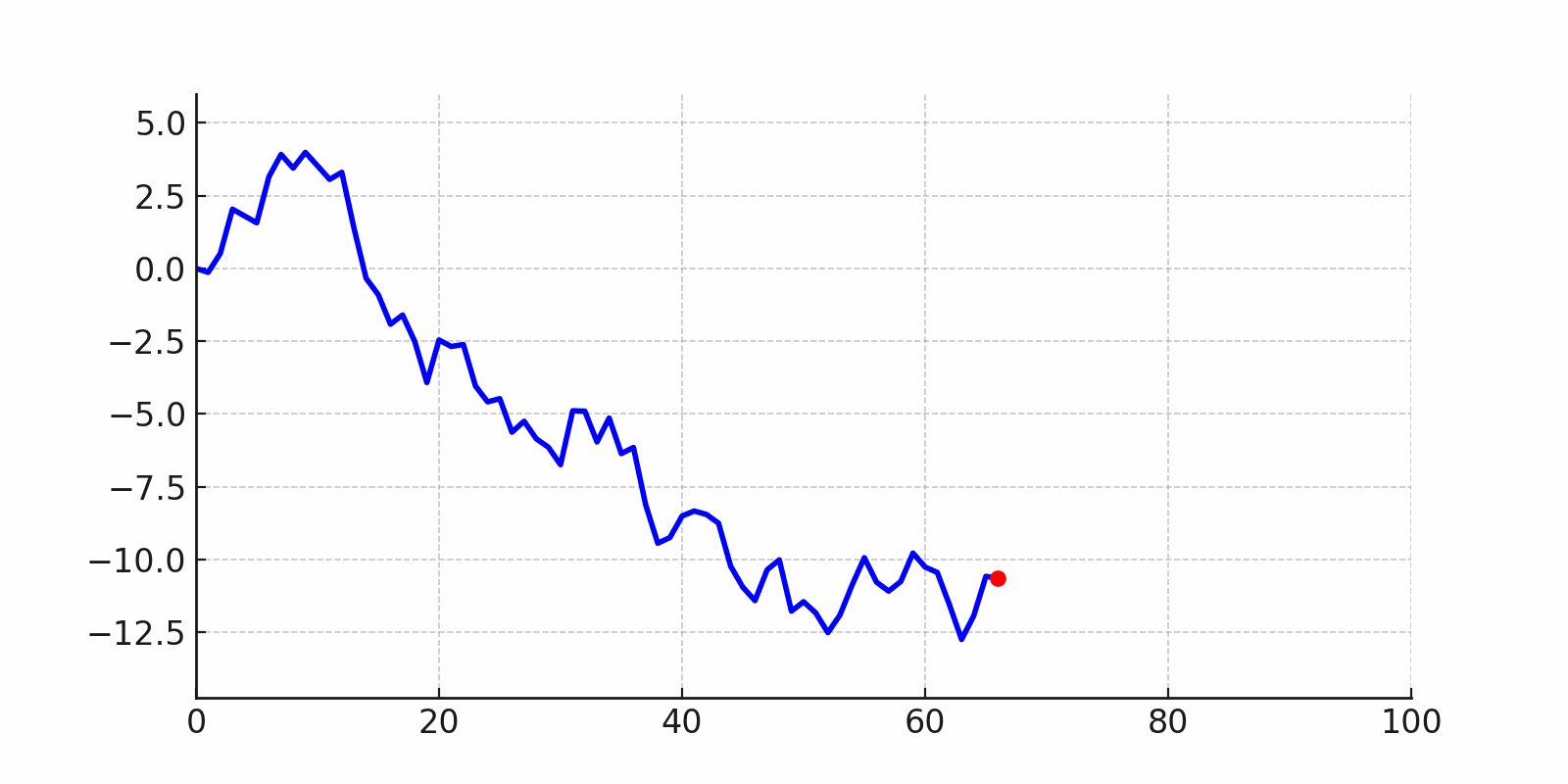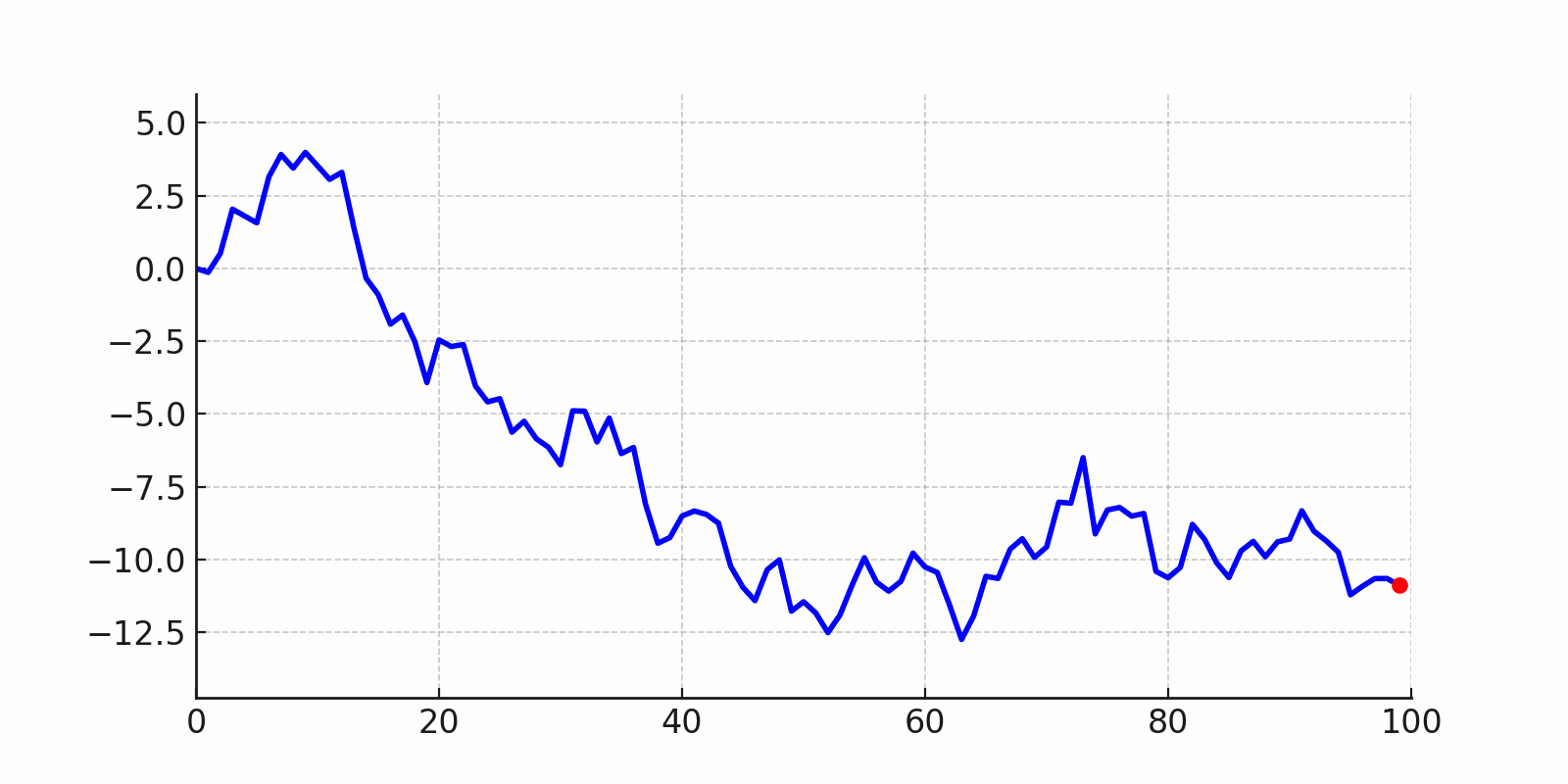
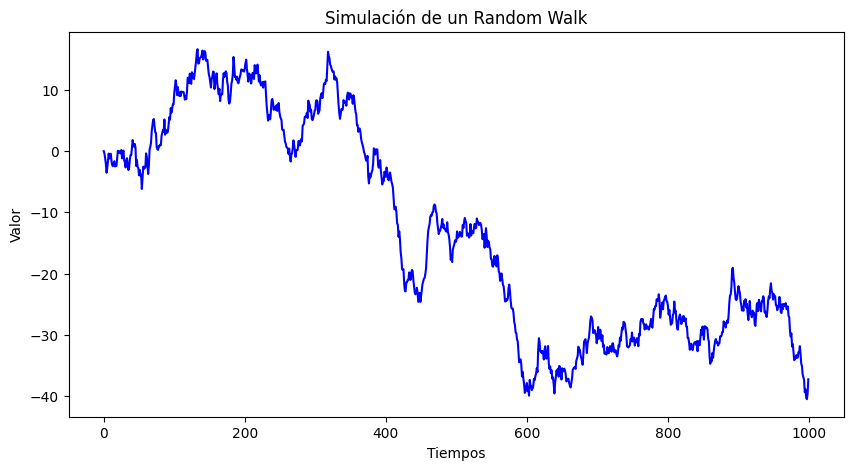
random_walk_process#
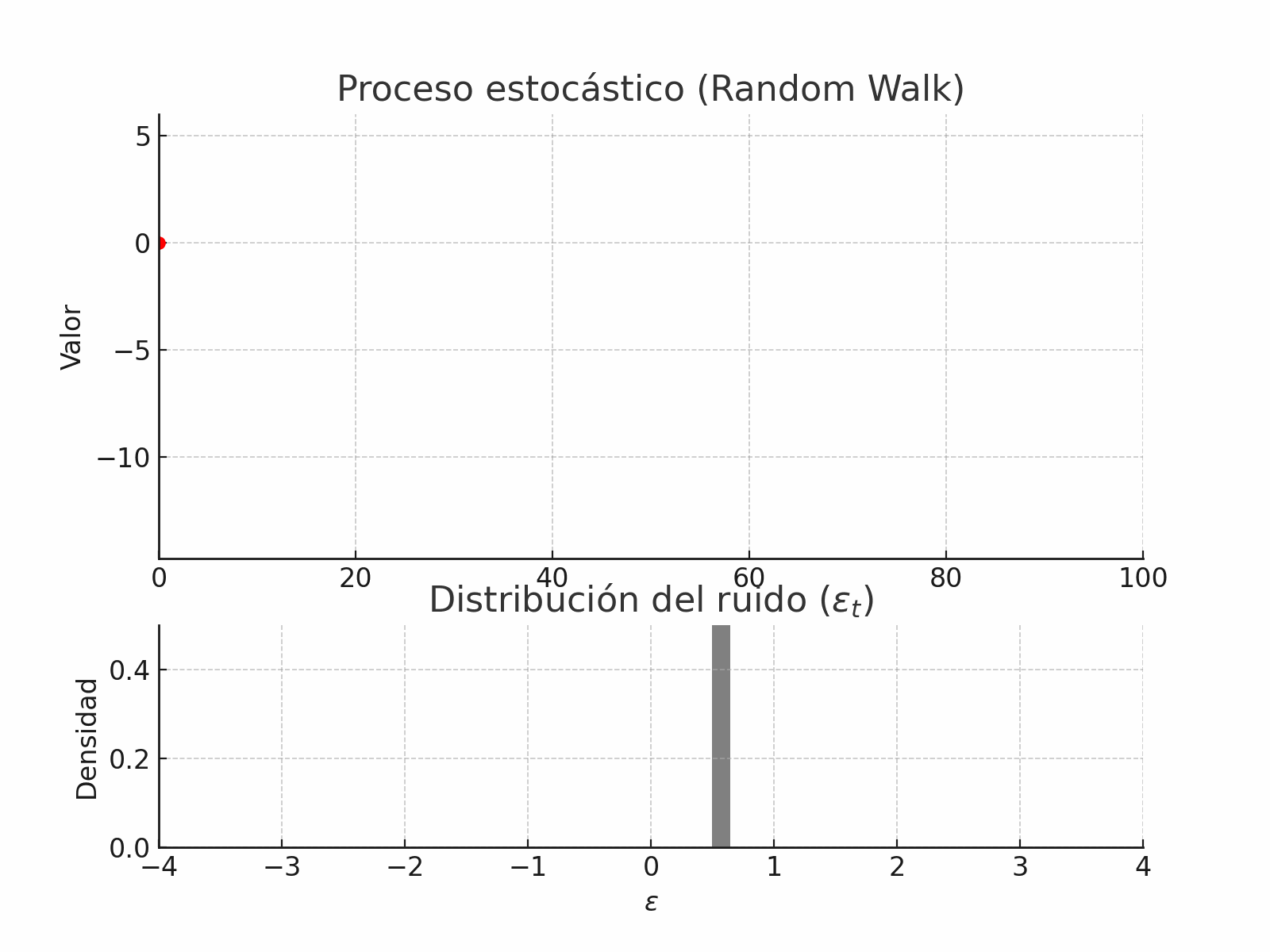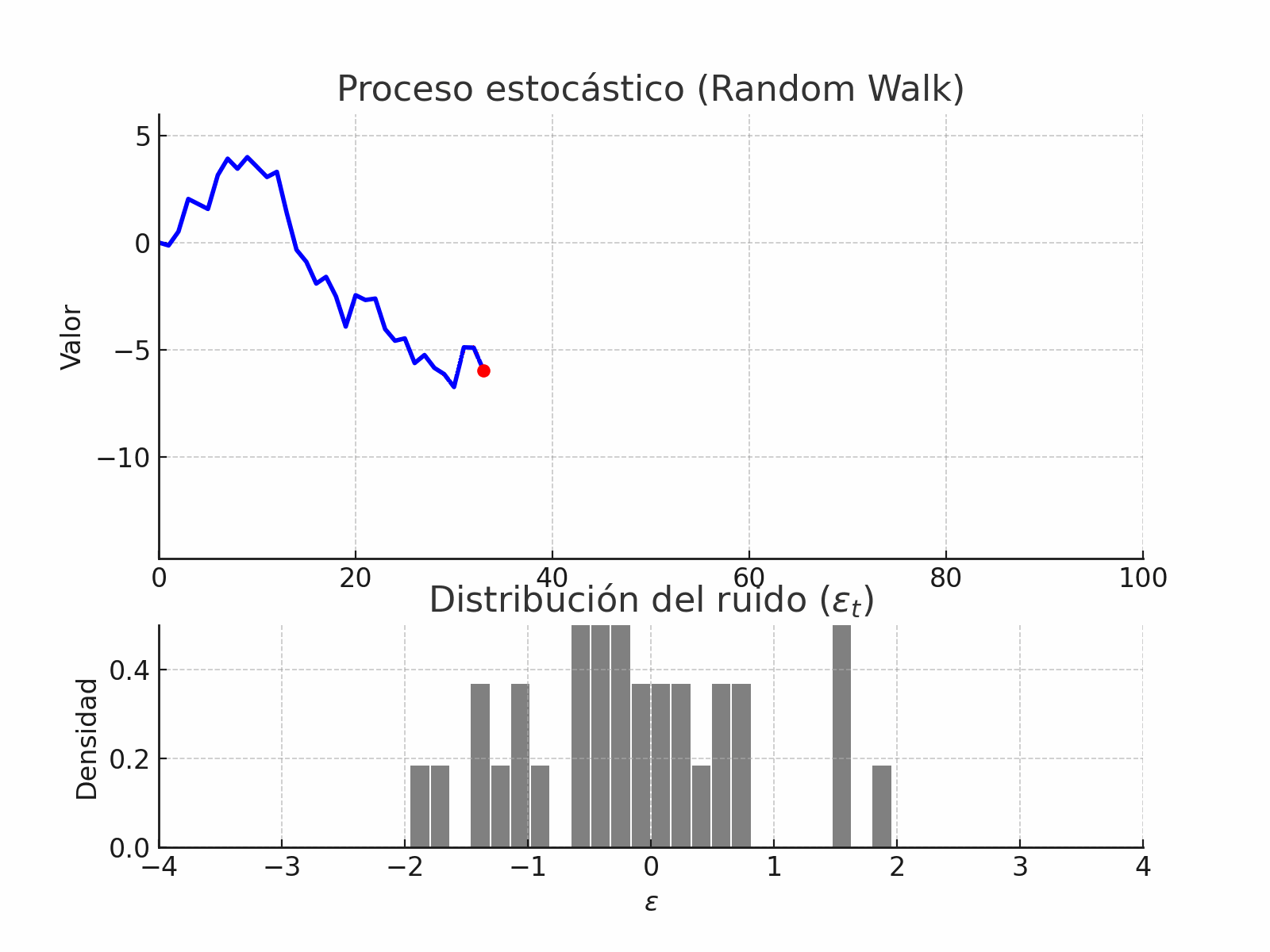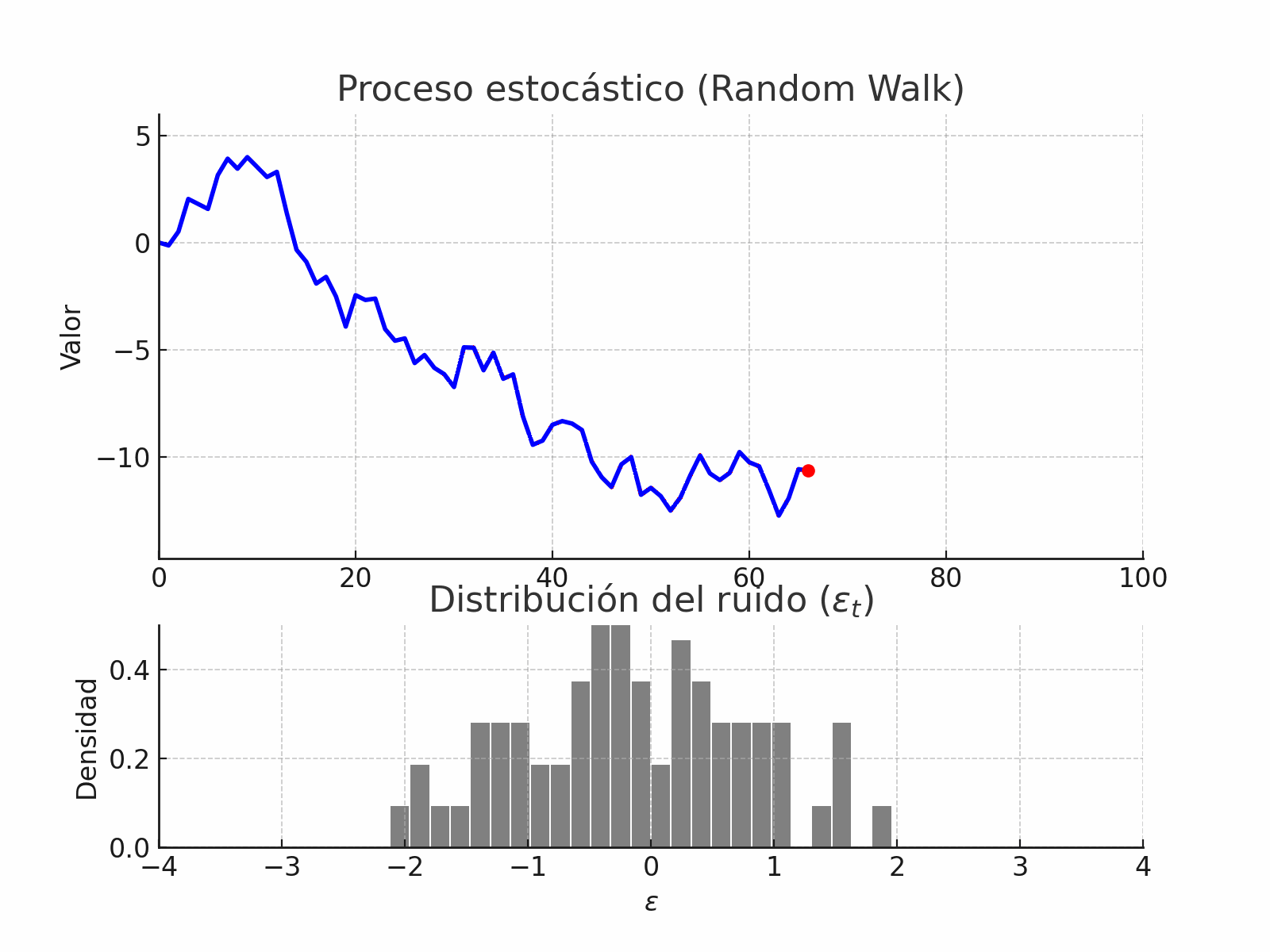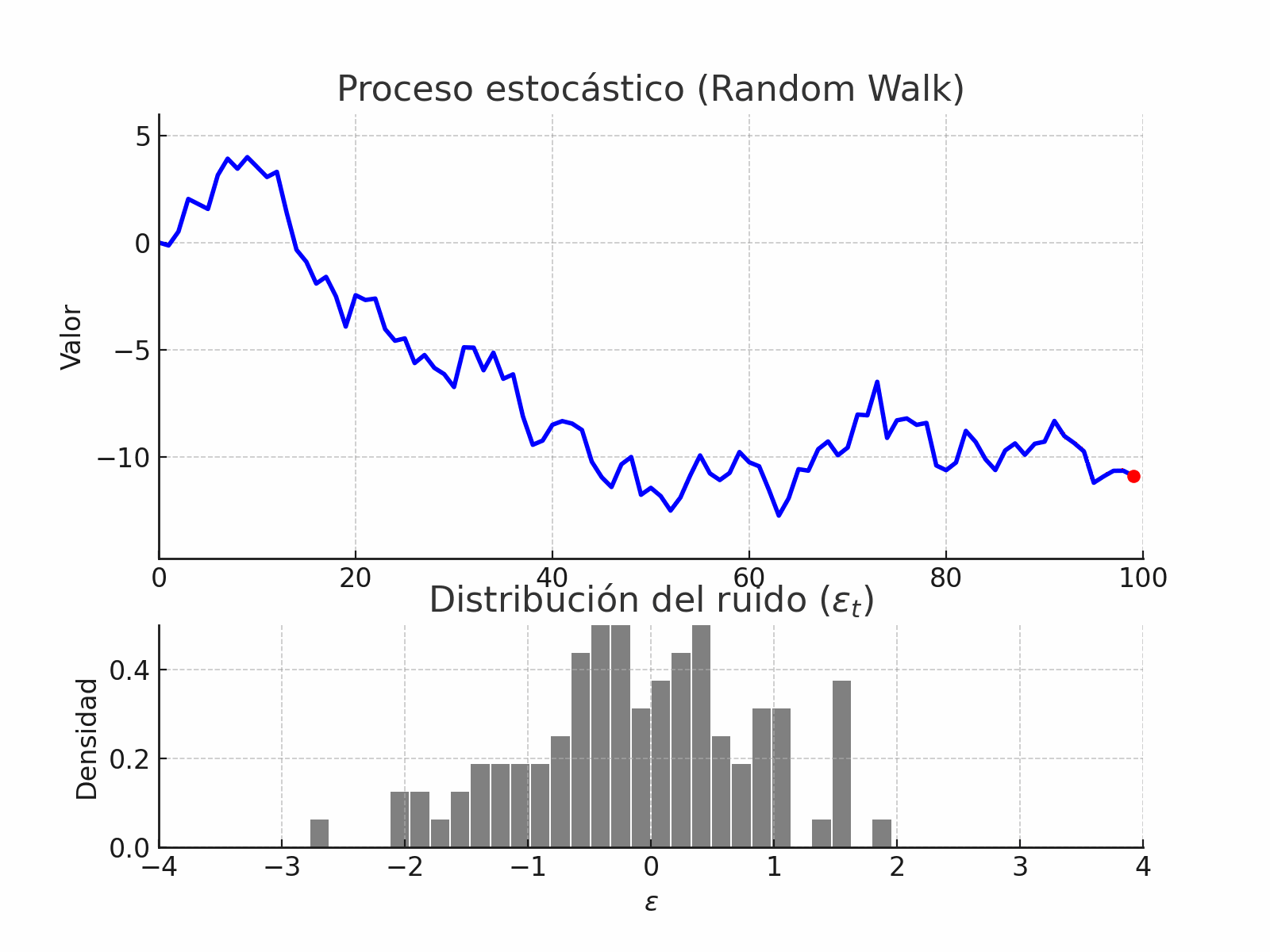
random_walk_with_noise#
import numpy as np
import matplotlib.pyplot as plt
# Semilla para reproducibilidad
np.random.seed(35)
# 1000 pasos de ruido blanco
steps = np.random.standard_normal(1000)
steps[0] = 0 # primer valor en cero
# Random Walk = suma acumulada
random_walk = np.cumsum(steps)
# Graficar
plt.figure(figsize=(10,5))
plt.plot(random_walk, color="blue")
plt.xlabel("Tiempos")
plt.ylabel("Valor")
plt.title("Simulación de un Random Walk")
plt.show()
Importancia del random walk y los procesos estocásticos en series de tiempo
Los procesos estocásticos son fundamentales en el análisis de series de tiempo porque permiten modelar fenómenos que evolucionan con incertidumbre en el tiempo. En el mundo real, muchas variables —como los precios de acciones, la inflación, la temperatura o la demanda energética— no siguen patrones deterministas, sino que presentan componentes aleatorios que solo pueden describirse mediante modelos probabilísticos.
Dentro de estos procesos, el random walk (camino aleatorio) es uno de los más relevantes, especialmente en finanzas y economía.
¿Por qué es tan importante el random walk?
El random walk es el modelo base de muchas series no estacionarias. Si una serie sigue un random walk, sus propiedades estadísticas (como la media o la varianza) cambian con el tiempo, lo que tiene grandes implicaciones para el modelado y el pronóstico.
En finanzas, se utiliza para describir el comportamiento de los precios de activos, bajo la hipótesis de eficiencia de mercado:
Los cambios en el precio son aleatorios porque toda la información disponible ya está reflejada en el precio actual.
Cuando una serie sigue un random walk, no es predecible en el sentido clásico:
El mejor pronóstico para el siguiente valor es simplemente el último valor observado.
No hay una “tendencia verdadera”, aunque pueda parecer que la hay en el corto plazo.
¿Qué pasa si no se reconoce un random walk?
Si intentamos aplicar modelos que asumen estacionariedad (como AR, MA o ARMA) a una serie que sigue un random walk, los resultados serán inválidos.
También corremos el riesgo de detectar falsas relaciones entre variables, conocidas como regresiones espurias.
Aplicaciones prácticas del concepto
Detección de no estacionariedad: El primer paso en el análisis de cualquier serie de tiempo es determinar si sigue un random walk. Para esto se usan pruebas como ADF (Augmented Dickey-Fuller) o KPSS.
Transformaciones previas al modelado: Si una serie sigue un random walk, debe transformarse (por ejemplo, mediante diferenciación) antes de aplicar modelos de pronóstico.
Modelos financieros: El random walk es la base de modelos como el modelo de caminata aleatoria con drift, el modelo de Black-Scholes y los procesos de Geometric Brownian Motion.