Análisis de Componentes Principales-PCA

El Análisis de Componentes Principales (PCA-Principal Components Analysis) es una técnica de reducción de dimensionalidad que se utiliza para transformar un conjunto de observaciones de variables posiblemente correlacionadas en un conjunto de valores de variables linealmente no correlacionadas, llamadas componentes principales. El objetivo es conservar la mayor parte de la variabilidad presente en los datos originales utilizando un número reducido de componentes principales.

PCA identifica el eje que representa la mayor cantidad de varianza en el conjunto de entrenamiento. Luego encuentra un segundo eje, ortogonal al primero, que representa la mayor cantidad de varianza restante. En un conjunto de datos bidimensional, esto es sencillo de visualizar; para conjuntos de datos de mayor dimensión, PCA encuentra tantos ejes como dimensiones haya en el conjunto de datos.

Para cada componente principal, PCA encuentra un vector unitario centrado en cero que apunta en la dirección de la componente principal. La dirección de los vectores unitarios puede no ser estable si se perturba ligeramente el conjunto de entrenamiento y se ejecuta PCA nuevamente, pero generalmente permanecerán en los mismos ejes.

Supongamos que tenemos una base de datos con cinco variables, cada variable es una dimensión, entonces tenemos cinco dimensiones. Con PCA podemos reducir la dimensionalidad de la base de datos, por ejemplo, a dos dimensiones. PCA logra que estas dos nuevas variables puedan resumir la mayor proporción de la variabilidad de la información original. Estas nuevas variables se llaman Componentes Principales. La siguiente figura muestra cómo las variables originales se pueden expresar en dos nuevos ejes llamados Componente 1 y Componente 2; sin embargo, el Componente Principal 1 es el más importante porque recoge más información. Este análisis se realiza con la matriz de varianzas-covarianzas del conjunto de datos.

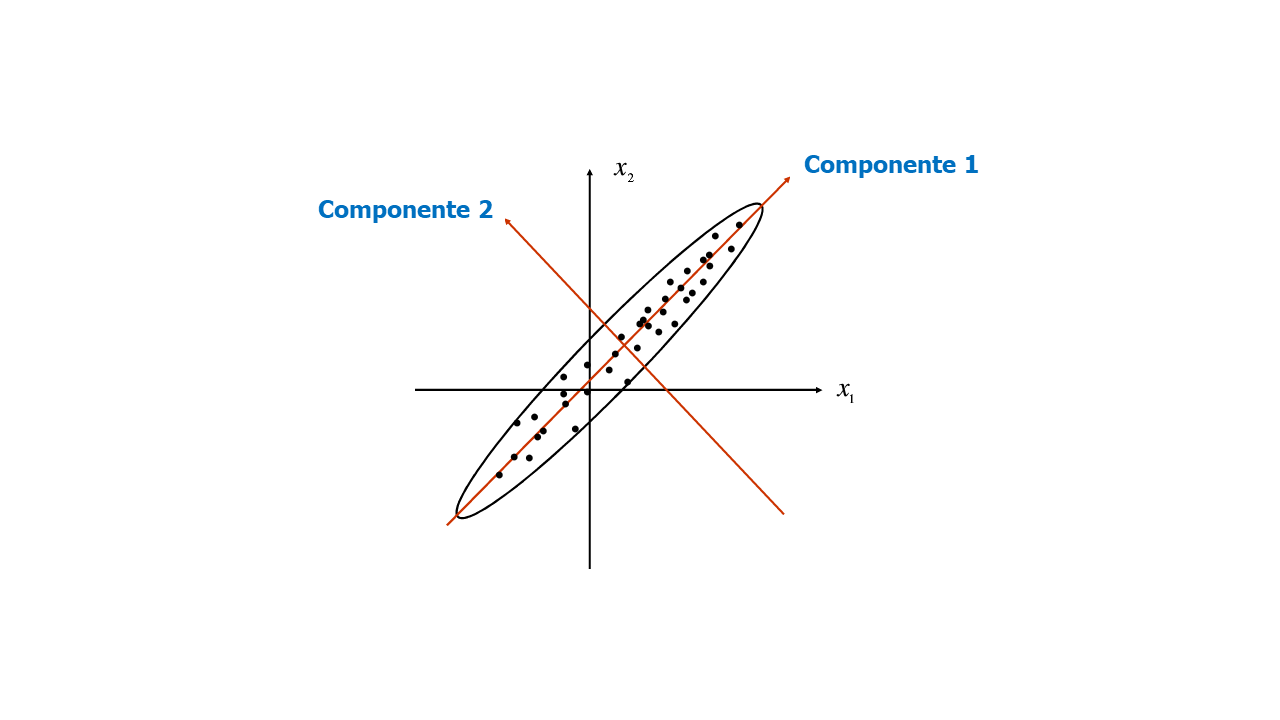
Componentes

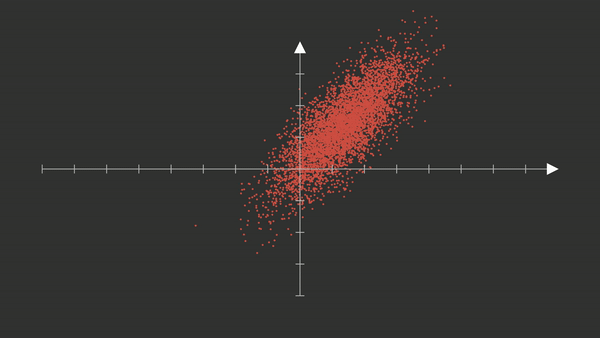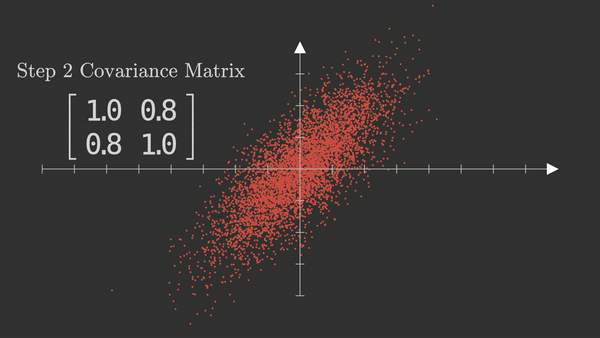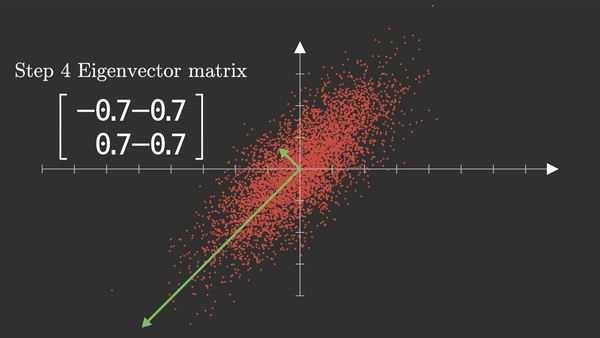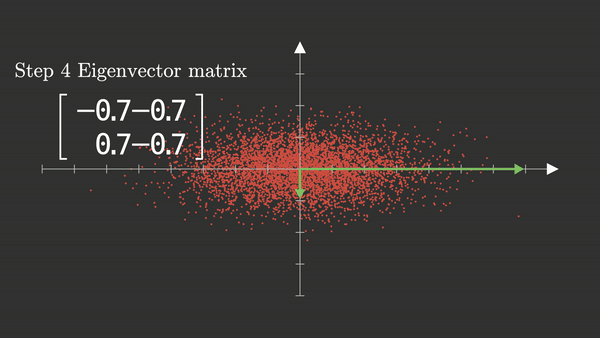
PCA_1

PCA_2

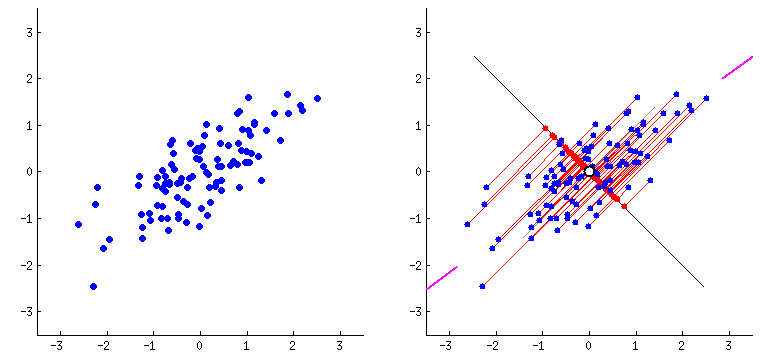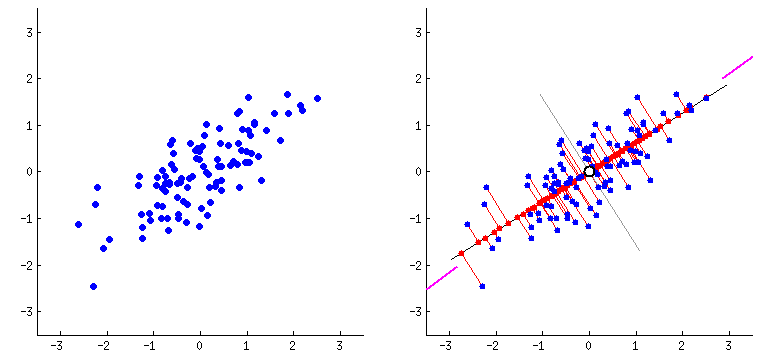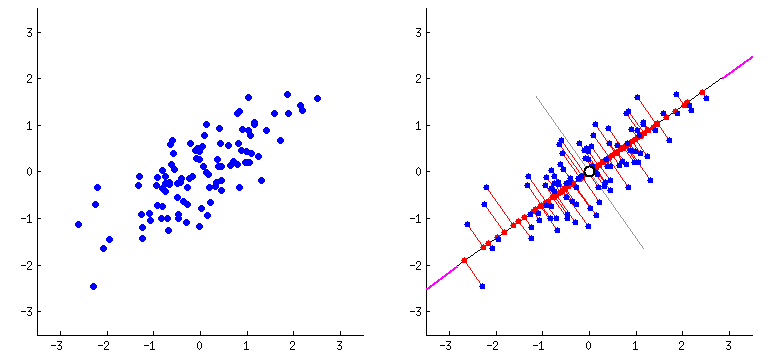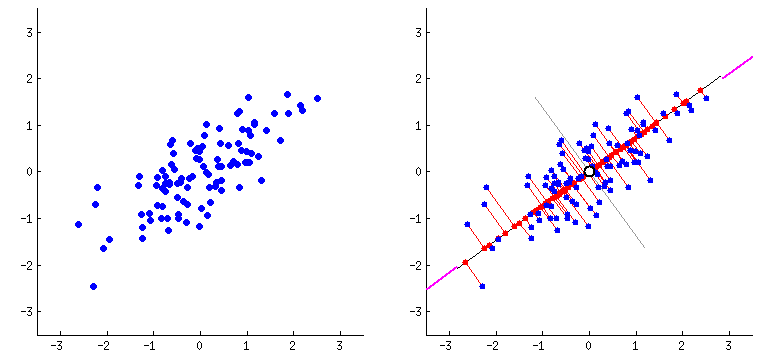
Los Componentes Principales son los Eigenvectores de la matriz de varianzas-covarianzas de las variables originales y se convertirán en los nuevos ejes. El ángulo entre los Eigenvectores es de 90°, así que los Eigenvectores son ortogonales entre sí.

La matriz de varianzas-covarianzas es simétrica, del orden \(nxn\), las varianzas, \((\sigma^2_{ij})\), de cada variable están en la diagonal de la matriz, los demás valores son las covarianzas, \((\sigma_{ij})\).

\[\begin{split} \sum = \begin{bmatrix} \sigma^2_{11} & \sigma_{12} & ... & \sigma_{1p} \\ \sigma_{21} & \sigma^2_{22} & ... & \sigma_{2p} \\ ... & ... & ... & ... \\ \sigma_{n1} & \sigma^2_{n2} & ... & \sigma_{np} \end{bmatrix}\end{split}\]

Para \(p\) variables, se extraen \(p\) Eigenvectores y \(p\) Eigenvalores. Estos Eigenvectores son las Componentes Principales y el Eigenvector asociado a cada Componente Principal es la proporción de la varianza total que ese componente puede explicar.

En el ACP no se generan variables nuevas, sino que se transforman en nuevas combinaciones lineales. Por lo anterior, la varianza total de las variables originales sigue siendo la misma.

Técnicamente, PCA implica la rotación del sistema de coordenadas original a un nuevo sistema de coordenadas con propiedades estadísticas deseables. Más precisamente, se busca definir una transformación ortogonal a una matriz de covarianza diagonal. Computacionalmente, PCA se reduce a resolver los valores propios y los vectores propios de una matriz definida positiva mediante un proceso generalmente denominado análisis de valores propios o descomposición espectral.

Este proceso de extracción de características se utiliza tanto para optimizar el espacio de almacenamiento y la eficiencia computacional del algoritmo de aprendizaje, como para mejorar el rendimiento predictivo al reducir la maldición de la dimensionalidad.

Ejemplo:

Supongamos la siguiente matriz de varianzas-covarianzas de un conjunto de dos variables:

\[\begin{split}\sum = \begin{bmatrix} 0,00761 & 0,00331\\ 0,00331 & 0,00840 \end{bmatrix}\end{split}\]

La varianza de la variable 1 es igual a 0,00761 y la varianza de la variable 2 es 0,00840. La sumatoria de la varianza del conjunto de datos es de 0,01601 \((0,00761+0,00840)\).

Eigenvalores:

Eigenvalores \(\lambda_i\): varianzas de cada Componente.

\[\lambda_1 = 0,0113385\]

\[\lambda_2 = 0,00467151\]

El Componente Principal 1 es el más importante porque es el de mayor Eigenvalor. Los Eigenvalores son las varianzas de cada Componente Principal y la suma de los Eigenvalores es la suma de las varianzas de las variables originales, es decir, es la varianza total, la cual es 0,01601 \((0,0113385+0,00467151)\).

El Componente Principal 1 explica el 70,82% de la variabilidad total. Recuerde que la sumatoria de los \(\lambda\) es igual a la sumatoria de las varianzas de las variables. El analista puede decidir en trabajar solo con esta Componente y así se reduciría la dimensionalidad de los datos. Este es el objetivo del ACP, encontrar la menor cantidad de componentes posibles que puedan explicar la mayor parte de la variación original. En otras palabras, con el ACP se busca representar la \(p\) variables en un número menor de variables (Componentes) conformadas como combinaciones lineales de las originales y perder la menor cantidad de información.

Al aplicar el ACP, las variables originales correlacionadas se transforman en variables no correlacionadas.

• Proporción de la varianza de la Componente Principal 1:

\[\frac{\lambda_1}{\sum{\lambda_i}} = \frac{0,0113385}{0,0113385+0,00467151} = 0,7082\]

• Proporción de la varianza de la Componente Principal 2:

\[\frac{\lambda_2}{\sum{\lambda_i}} = \frac{0,00467151}{0,0113385+0,00467151} = 0,2918\]

Como la desviación estándar es la raíz cuadrada de la varianza, cada Componente Principal tiene la siguiente desviación estándar.

• Desviación estándar Componente Principal 1:

\[\sqrt{\lambda_1} = \sqrt{0,0113385} = 0,1065\]

• Desviación estándar Componente Principal 2:

\[\sqrt{\lambda_2} = \sqrt{0,00467151} = 0,0683\]

Eigenvectores:

Eigenvectores: Cargas de cada Componente.

\[\begin{split}Eigenvector_1 = \begin{bmatrix} 0,6638921 \\ 0,7478284 \end{bmatrix}\end{split}\]

\[\begin{split}Eigenvector_2 = \begin{bmatrix} -0,7478284 \\ 0,6638921 \end{bmatrix}\end{split}\]

Las cargas de un Componente Principal son los elementos del vector propio que forman la componente. Cada componente es una combinación lineal de las variables del conjunto de datos.

El primer elemento de \(Eigenvector_1\) es 0,6638921, esta es la carga o score para la primera variable original. El segundo elemento es la carga que se le asigna a la segunda variable de la base de datos.

A la matriz que se conforma con los Eigenvectores se llama matriz de rotación.

Cada vector propio debe tener una longitud igual a 1,0. Esto se comprueba si la suma de cada elemento (cargas) al cuadrado es igual a 1,0. Esta condición es una restricción del modelo porque con el valor de 1,0 las varianzas no se modifican.

Significado de las cargas:

Las cargas, también conocidas como “loadings” en inglés, son los coeficientes que indican la contribución de cada variable original a una componente principal. En otras palabras, las cargas representan la correlación entre las variables originales y las componentes principales.

Las cargas indican cómo se combinan las variables originales para formar los nuevos componentes principales.

Interpretación de las Cargas:

• Valores absolutos: Las cargas absolutas indican la magnitud de la contribución de cada variable original a la componente principal.

• Signos: Los signos de las cargas indican la dirección de la relación. Una carga positiva indica que la variable y la componente principal están positivamente correlacionadas, mientras que una carga negativa indica una correlación negativa.

Las cargas son esenciales para comprender e interpretar los resultados de PCA, ya que proporcionan una conexión directa entre las variables originales y las componentes principales.

Biplot:

Un biplot es una combinación de un scatter plot de las puntuaciones de las componentes principales y una visualización de las cargas (coeficientes) de las variables originales. Esto ayuda a interpretar cómo las variables originales contribuyen a las componentes principales.

Biplot

Elementos del Biplot:

1. Puntos de datos (azul): Cada punto en el biplot representa una observación en el espacio de las componentes principales. La posición de los puntos refleja cómo se agrupan las observaciones basadas en las nuevas dimensiones formadas por las componentes principales.

2. Vectores (flechas rojas): Cada vector representa una variable original. La dirección y longitud del vector indican la contribución y la importancia de la variable a las componentes principales. Un vector largo sugiere que la variable tiene una fuerte influencia en esa dirección de la componente principal correspondiente.

3 Ejes de Componentes Principales: Los ejes PC1 y PC2 (Componente Principal 1 y Componente Principal 2) representan las dos primeras componentes principales, que son combinaciones lineales de las variables originales.

Unidades de las variables:

Cuando se tienen variables con magnitudes grandes y otras pequeñas, se tiene un problema porque las variables de magnitud mayor van a predominar en la reducción de dimensionalidad y además, estas variables tienen mayor varianza. También, la covarianza entre las variables será mayor por la magnitud, siendo esto en muchos casos un resultado errado porque la covarianza estaría afectada por las unidades de las variables con unidades mayores y no por el co-movimiento.

Para solucionar esto tenemos dos opciones:

1. Cambio de escala de las variables:

\[Estandarización = X_{stand} = \frac{x_i-mín(x)}{máx(x)-mín(x)}\]

2. Matriz de correlaciones: realizar el ACP sobre la matriz de coeficientes de correlación en lugar de la matriz de varianzas-covarianzas.

\[\begin{split} \sum = \begin{bmatrix} \rho_{11} & \rho_{12} & ... & \rho_{1p} \\ \rho_{21} & \rho_{22} & ... & \rho_{2p} \\ ... & ... & ... & ... \\ \rho_{n1} & \rho_{n2} & ... & \rho_{np} \end{bmatrix}\end{split}\]

Como la diagonal tiene valores de 1,0, la suma de la diagonal es igual a \(p\), cantidad de variables.

Elegir el número correcto de dimensiones:

En lugar de elegir arbitrariamente el número de dimensiones a reducir, es más sencillo elegir el número de dimensiones que sumen una porción suficientemente grande de la varianza (por ejemplo, el 80% o 95%). A menos que, por supuesto, estés reduciendo la dimensionalidad para la visualización de datos, en cuyo caso querrás reducir la dimensionalidad a 2 o 3.

Para esto se puede generar un gráfico que muestre la varianza explicada acumulada en función del número de componentes principales. La línea en el gráfico muestra cómo la varianza explicada se acumula a medida que se agregan más componentes principales. Al inicio, la varianza explicada aumenta rápidamente, lo que indica que las primeras componentes capturan la mayor parte de la variabilidad en los datos.

En muchos casos, hay un “punto de codo” en el gráfico donde la tasa de aumento de la varianza explicada se reduce significativamente. Este punto puede ser útil para determinar el número óptimo de componentes principales a utilizar, ya que más allá de este punto, agregar más componentes no proporciona una ganancia significativa en la varianza explicada.

Codo

Pruebas:

La suma de las cargas de cada componente al cuadrado debe ser igual a 1,0:

Si los vectores son ortogonales, entonces el producto escalar de los vectores es igual a cero:

\(\sum{\lambda_i} = \sum{var_i}\): la suma de las varianzas de las variables es igual a la suma de los Eigenvalores.