Estacionariedad#
La estacionariedad es uno de los conceptos más importantes en el análisis de series de tiempo.
Muchos modelos clásicos, como ARMA, ARIMA o SARIMA, requieren que la serie sea estacionaria, es decir, que sus propiedades estadísticas no cambien a lo largo del tiempo.
Estacionariedad estricta
Un proceso estocástico \(\{y_t\}\) es estrictamente estacionario si toda su distribución conjunta es invariante ante traslaciones en el tiempo.
Esto significa que para cualquier conjunto de tiempos \(t_1, t_2, \dots, t_k\), se cumple:
para todo \(h \in \mathbb{Z}\).
En esta definición, \(\overset{d}{=}\) indica igualdad en distribución conjunta.
Esta condición es fuerte y difícil de verificar en la práctica, ya que requiere conocer toda la función de distribución conjunta.
Estacionariedad débil (de segundo orden)
Por eso, en aplicaciones prácticas usamos una forma más manejable: la estacionariedad débil o de segundo orden.
Un proceso \(\{y_t\}\) es débilmente estacionario si cumple las siguientes tres condiciones:
Tiene media constante:
\[\mathbb{E}[y_t] = \mu \quad \forall t\]Tiene varianza constante:
\[\text{Var}(y_t) = \sigma^2 \quad \forall t\]La covarianza entre dos observaciones depende únicamente del rezago \(k\) y no del tiempo \(t\):
\[\text{Cov}(y_t, y_{t-k}) = \gamma_k \quad \forall t\]
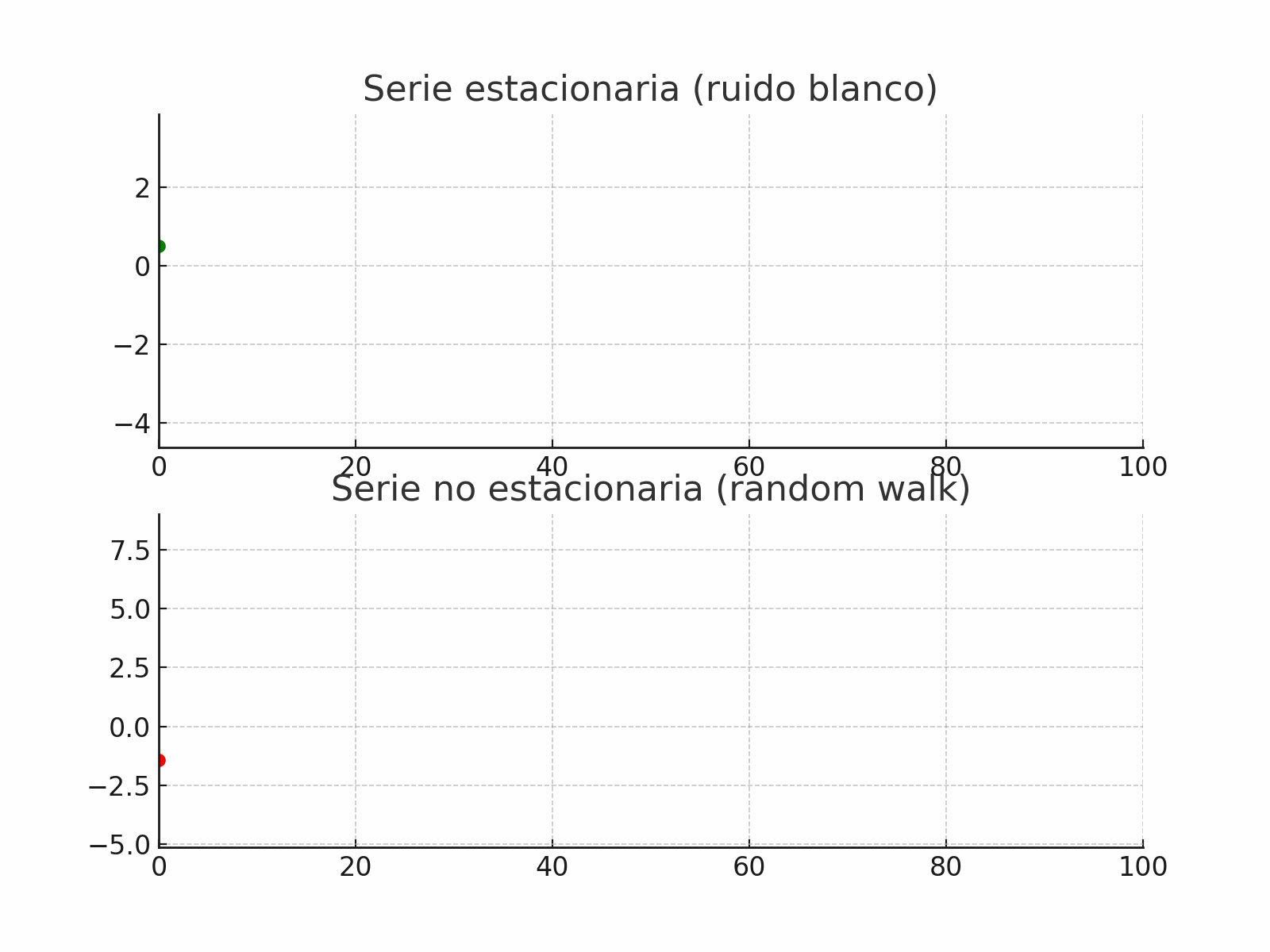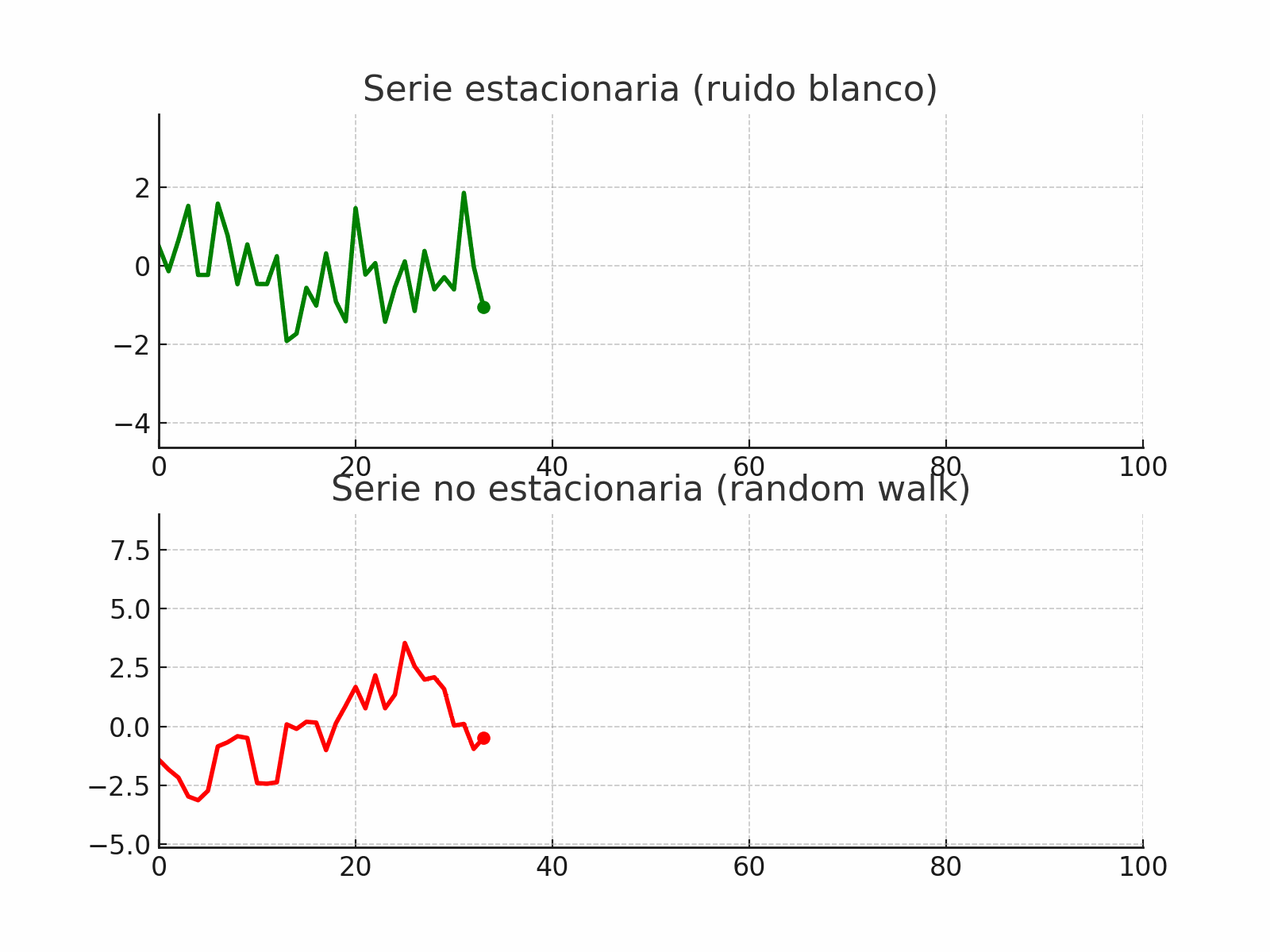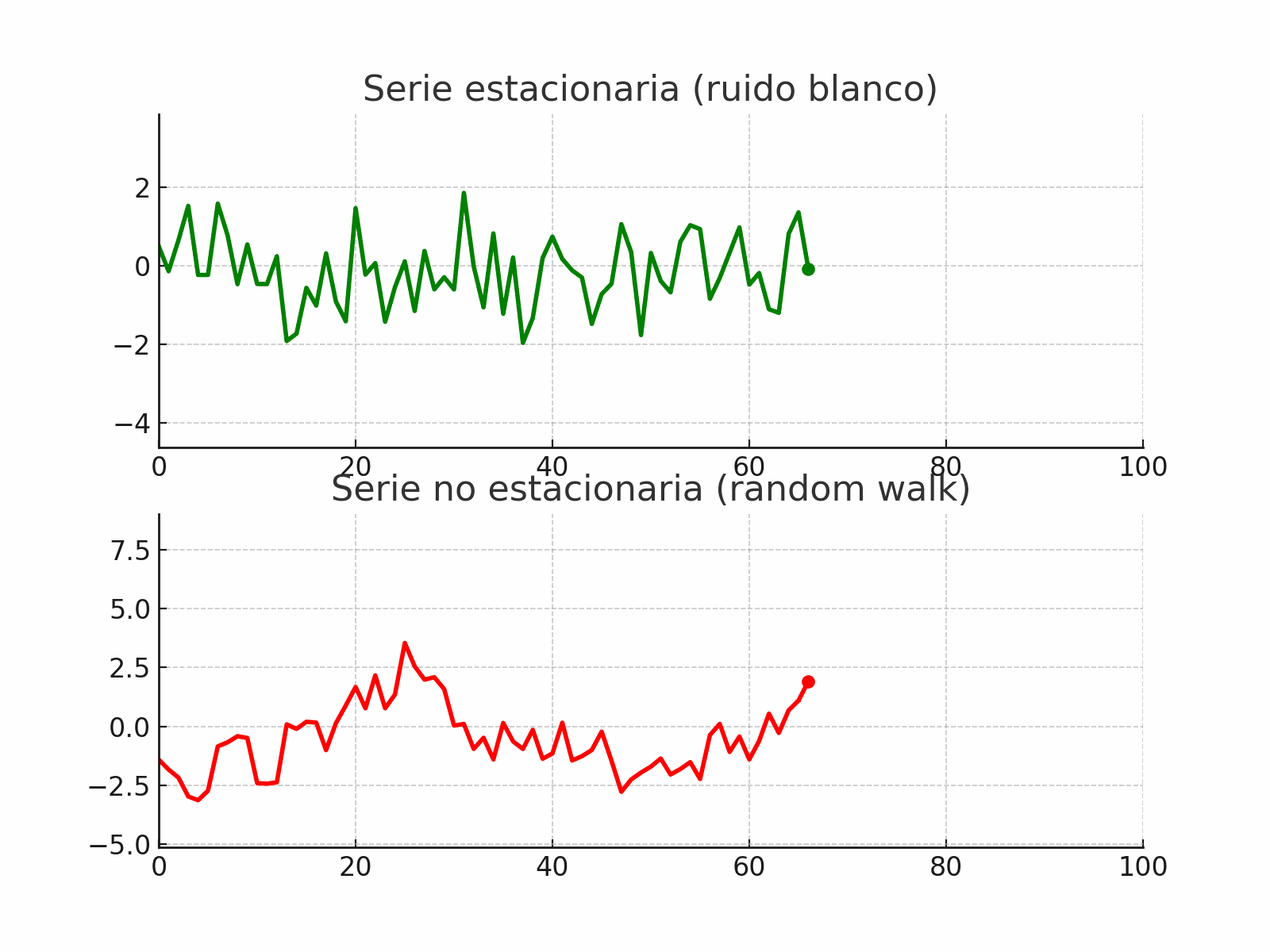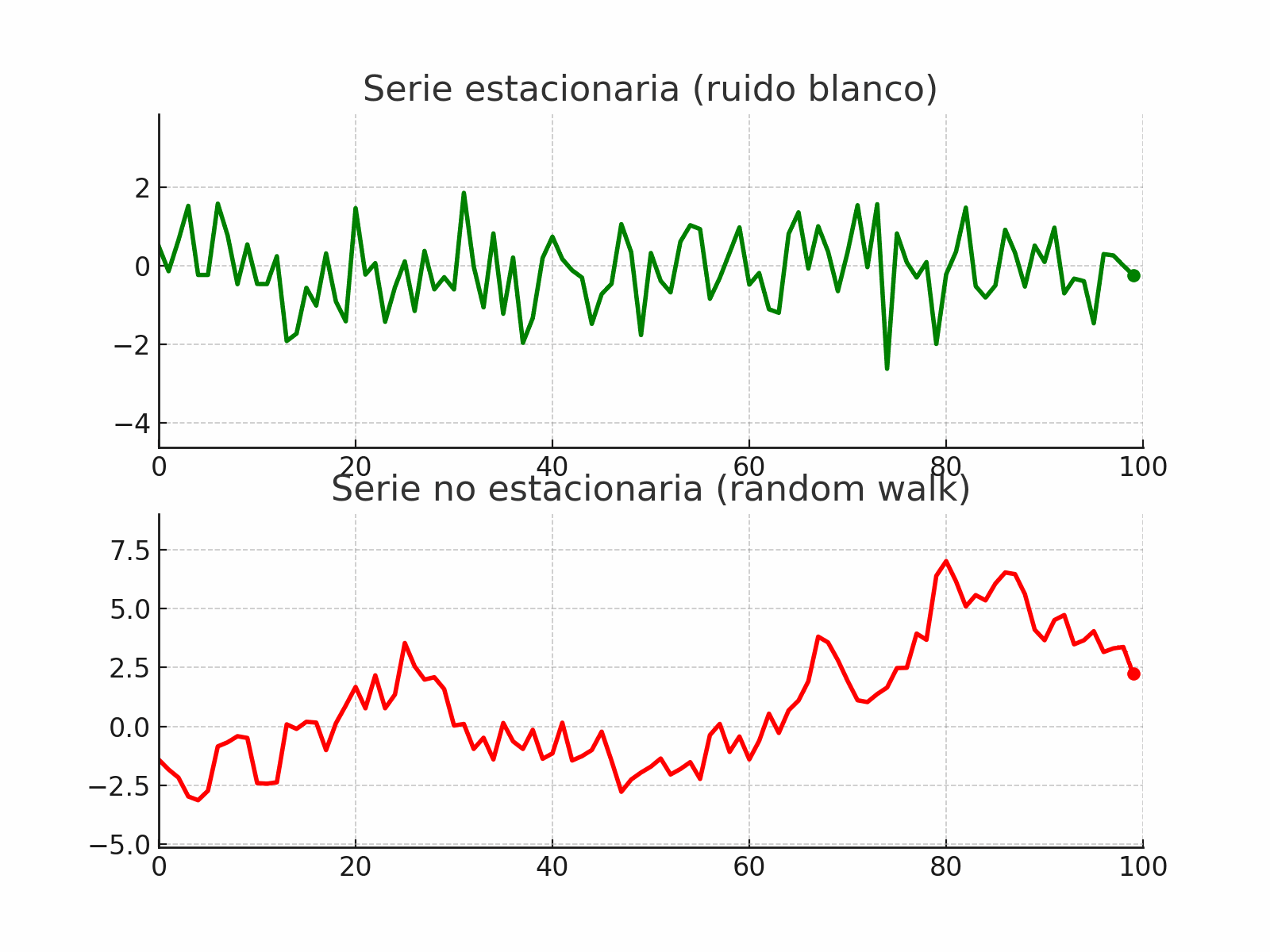
stationarity_vs_nonstationarity#
Ejemplos de series no estacionarias
Una serie con tendencia determinista, como \(y_t = \alpha t + \varepsilon_t\), tiene media que cambia con el tiempo.
Un random walk definido como:
\[y_t = y_{t-1} + \varepsilon_t\]tiene varianza creciente en el tiempo, por lo tanto no es estacionario.
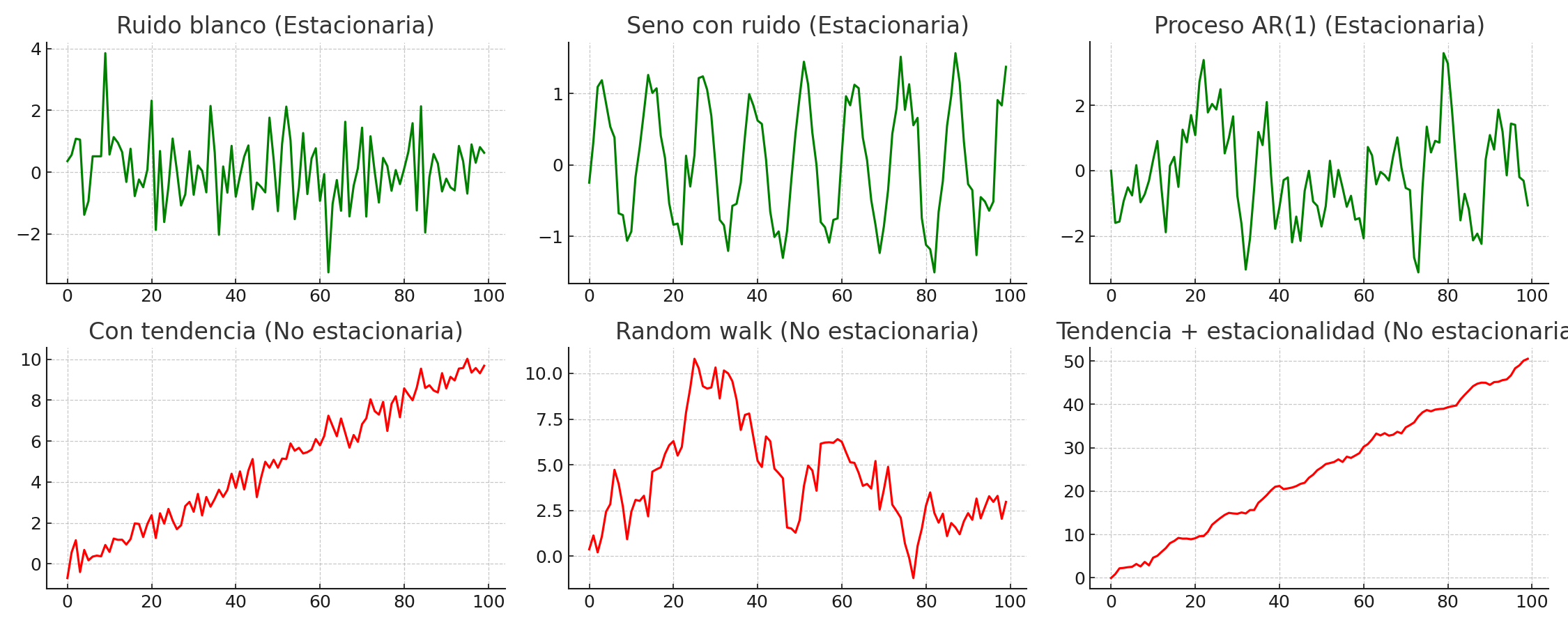
series_estacionarias_vs_no_estacionarias#
Prueba ADF (Augmented Dickey-Fuller):#
Para toda serie de tiempo es necesario verificar si es estacionaria o si se requieren transformaciones.
Para esto, existen pruebas estadísticas que permiten detectar la presencia de raíces unitarias, es decir, indicios de no estacionariedad. La más utilizada es la prueba ADF (Augmented Dickey-Fuller).
La prueba ADF evalúa la siguiente hipótesis:
Hipótesis nula \(H_0\): la serie tiene una raíz unitaria (no es estacionaria).
Hipótesis alternativa \(H_1\): la serie no tiene raíz unitaria (es estacionaria).
El modelo base sobre el que se realiza la prueba es:
donde:
\(C\) es una constante (puede ser cero).
\(\varepsilon_t\) es ruido blanco. Representa el error aleatorio o choque externo.
\(\alpha_1\) es el parámetro clave que indica si hay una raíz unitaria.
Interpretación de \(\alpha_1\)
Si \(|\alpha_1| < 1\), la serie es estacionaria.
Si \(\alpha_1 = 1\), hay una raíz unitaria, y la serie es no estacionaria.
Ejemplos:
Serie estacionaria:
\[y_t = 0.6 y_{t-1} + \varepsilon_t\]Aquí \(\alpha_1 = 0.6\), está dentro del círculo unitario, por lo tanto la serie es estacionaria.
Serie no estacionaria (random walk):
\[y_t = y_{t-1} + \varepsilon_t\]Aquí \(\alpha_1 = 1\), por lo tanto hay una raíz unitaria y la serie es no estacionaria.
Este es un random walk. Se puede reescribir como:
Esto quiere decir que:
El valor actual acumula todos los errores pasados.
No hay retorno al promedio.
La varianza crece con el tiempo → no es estacionario.
import numpy as np
import matplotlib.pyplot as plt
# Semilla para reproducibilidad
np.random.seed(35)
# Número de observaciones
n = 200
# Simular ruido blanco
eps = np.random.normal(0, 1, n)
# Inicializar series
y_stationary = np.zeros(n)
y_unit_root = np.zeros(n)
y_explosive = np.zeros(n)
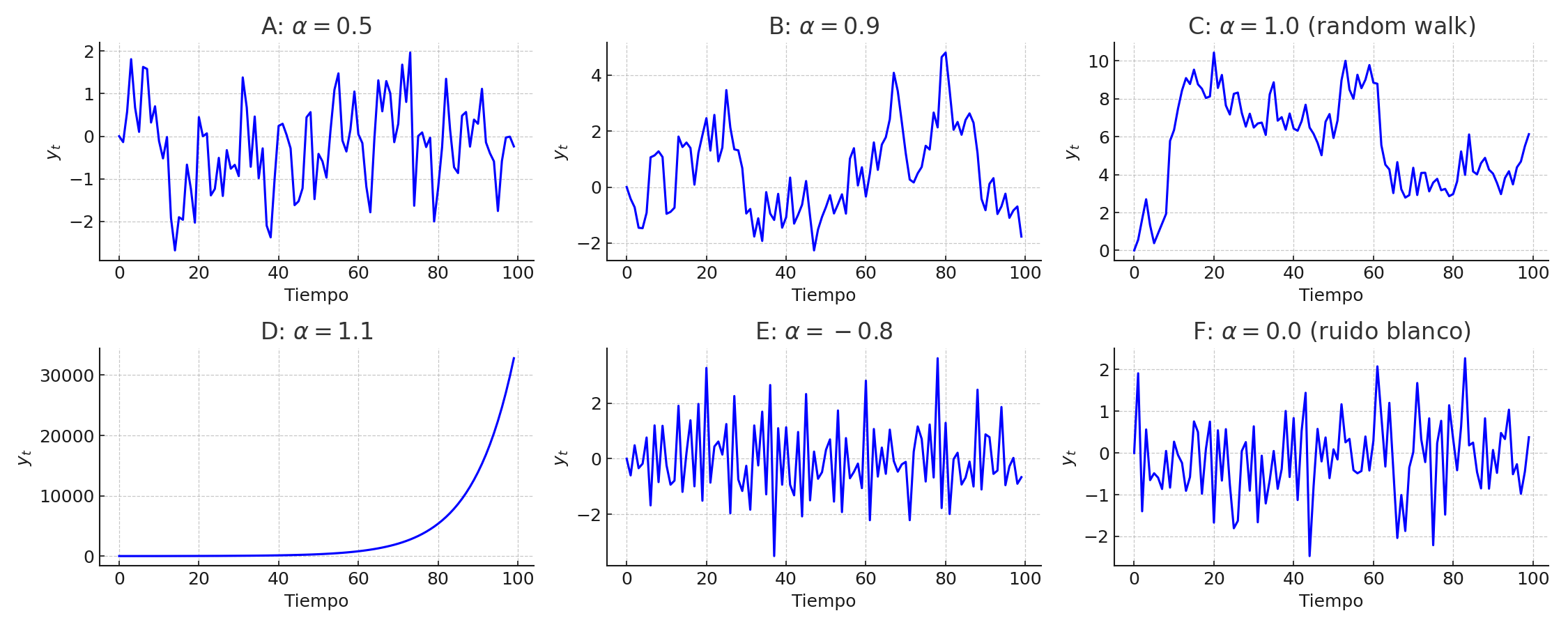
# Coeficientes
alpha_stationary = 0.6
alpha_unit_root = 1.0
alpha_explosive = 1.1
# Generar las tres series
for t in range(1, n):
y_stationary[t] = alpha_stationary * y_stationary[t - 1] + eps[t]
y_unit_root[t] = alpha_unit_root * y_unit_root[t - 1] + eps[t]
y_explosive[t] = alpha_explosive * y_explosive[t - 1] + eps[t]
# Graficar
plt.figure(figsize=(10, 5))
plt.plot(y_stationary, label='Estacionaria ($\\alpha = 0.6$)', color='green')
plt.plot(y_unit_root, label='Raíz unitaria ($\\alpha = 1.0$)', color='darkred')
# plt.plot(y_explosive, label='Explosiva ($\\alpha = 1.1$)', color='red')
plt.xlabel("Tiempo")
plt.ylabel("$y_t$")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
plt.figure(figsize=(10, 5))
plt.plot(y_explosive, label='Explosiva ($\\alpha = 1.1$)', color='red')
plt.title("Serie explosiva")
plt.xlabel("Tiempo")
plt.ylabel("$y_t$")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

Raíz unitaria#
Cuando hablamos de estacionariedad en series de tiempo, un concepto central es el de raíz unitaria. Este término proviene del análisis de ecuaciones de recurrencia o modelos autorregresivos.
Modelo autorregresivo AR(1)
Consideremos el siguiente modelo:
donde:
\(C\) es una constante,
\(\alpha_1\) es el coeficiente de autorregresión,
\(\varepsilon_t\) es ruido blanco.
Este modelo es llamado AR(1) porque depende de un solo valor pasado (\(y_{t-1}\)).
¿Qué significa la raíz de este proceso?
Podemos escribir el modelo en forma de ecuación característica:
Aplicando el operador rezago \(L\), donde \(L y_t = y_{t-1}\), se puede reescribir como:
Esto se llama forma operador o forma polinómica, donde el polinomio característico es:
Para analizar la estabilidad del sistema, sustituimos \(L\) por una variable \(z\):
y buscamos la raíz del polinomio, es decir, el valor que anula \(\Phi(z)\):
Esta raíz se analiza con respecto al círculo unitario del plano complejo.
Entonces no estamos buscando anular \(\varepsilon_t\), sino entender si la estructura \(\Phi(L)\) puede producir una serie que tienda a estabilizarse (estacionaria) o no (no estacionaria).
Lo que estamos haciendo es “aislar” la parte determinista (la estructura del modelo) en \(\Phi(L)\) y separarla del componente aleatorio \(\varepsilon_t\).
Lo que se quiere entender es cómo se comporta la serie \(y_t\) a lo largo del tiempo, dadas sus propias observaciones pasadas.
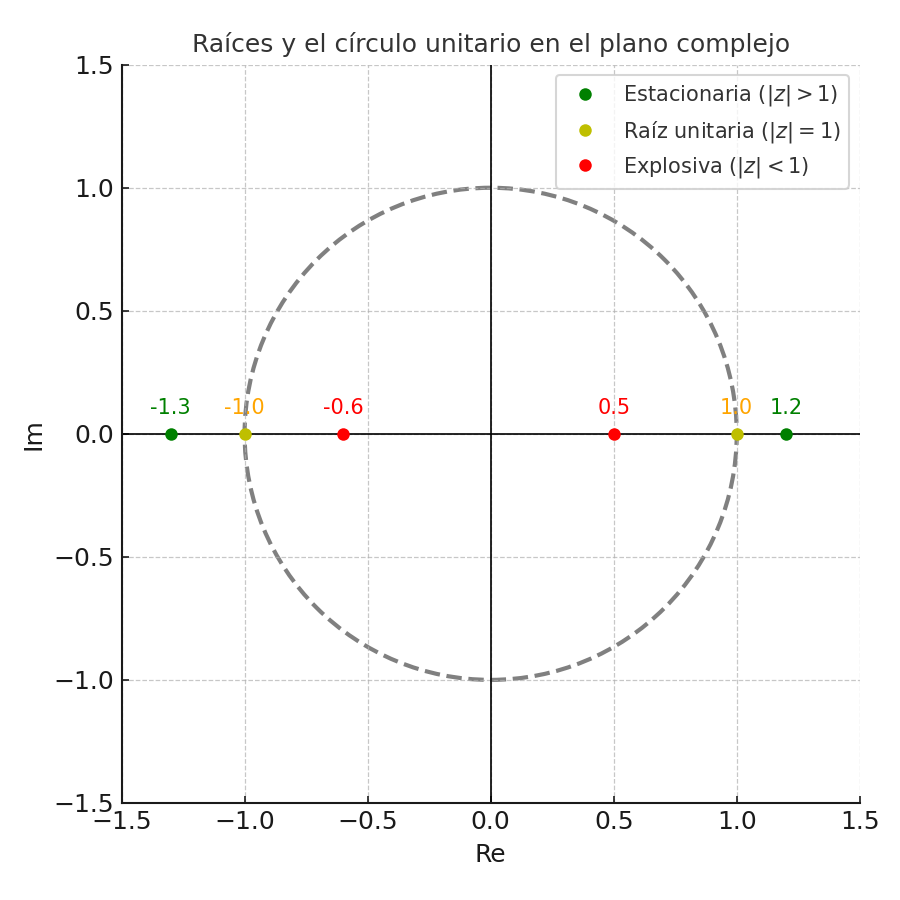
circulo_unitario_estacionariedad#
El círculo unitario
El círculo unitario es el conjunto de números complejos cuya magnitud es 1:
Una serie es estacionaria si todas las raíces de su polinomio característico están fuera del círculo unitario, es decir:
Equivalente a decir que:
¿Qué es una raíz unitaria?
Cuando:
entonces:
Este caso se llama raíz unitaria, y significa que la serie no es estacionaria.
Ejemplo:
Si \(\alpha_1 = 1\), el modelo es:
\[y_t = y_{t-1} + \varepsilon_t\]que es un random walk, claramente no estacionario.
Analogía simple
Piensa en el polinomio como una “función de equilibrio” del sistema. Si al resolver la ecuación el sistema tiende a volver al equilibrio (raíces fuera del círculo unitario), es estacionario.
Si el sistema queda vagando sin control (raíces dentro o sobre el círculo unitario), no es estacionario.
Resumen gráfico
Si \(|\alpha_1| < 1\): la raíz está fuera del círculo unitario → la serie es estacionaria.
Si \(|\alpha_1| = 1\): la raíz está sobre el círculo unitario → la serie tiene raíz unitaria, no estacionaria.
Si \(|\alpha_1| > 1\): la raíz está dentro del círculo unitario → el proceso es explosivo, también no estacionario.
Importancia práctica
Detectar raíces unitarias es esencial para saber si:
Se puede usar directamente un modelo ARMA.
Se necesita transformar la serie (por ejemplo, aplicar primeras diferencias).
Es válido aplicar pruebas de hipótesis o construir modelos de pronóstico.
Por eso, pruebas como ADF se centran en detectar si :math:`alpha_1 = 1`, es decir, si la serie tiene una raíz unitaria.
¿Por qué es importante la estacionariedad?
Permite que los modelos aprendan patrones estables en el tiempo, y que estos patrones sean válidos para hacer predicciones.
Si no se cumple, los errores de predicción se acumulan y los resultados son poco confiables.
Una serie no estacionaria puede producir resultados engañosos al hacer regresiones o pronósticos.
En particular, cuando dos series no estacionarias se correlacionan, es posible obtener una regresión espuria (una relación que parece significativa pero no lo es).
ejercicios_series_practica#
Resumen
La estacionariedad garantiza que los momentos estadísticos de la serie (media, varianza, covarianza) sean constantes en el tiempo.
Es un requisito esencial para aplicar la mayoría de modelos clásicos de series de tiempo.
Cuando no se cumple, la serie debe transformarse para poder modelarla adecuadamente.