Movimiento Browniano Geométrico (GBM) en Python#
El Movimiento Browniano Geométrico es un modelo matemático que se utiliza comúnmente para describir la evolución de los precios de los activos financieros, como las acciones. Este modelo combina la propiedad del crecimiento exponencial con la aleatoriedad del Movimiento Browniano, haciendo que sea especialmente útil para modelar el comportamiento de los precios de las acciones a lo largo del tiempo.
Ecuación Diferencial del GBM:
La dinámica de un activo bajo el modelo de Movimiento Browniano Geométrico se describe mediante la siguiente ecuación diferencial estocástica:
donde: - \(S_t\): Precio del activo en el tiempo \(t\). - \(\mu\): Tasa de retorno esperada del activo. - \(\sigma\): Volatilidad del activo. - \(dW_t\): Incremento del Movimiento Browniano estándar. - \(dt\): Incremento en el tiempo.
Solución de la Ecuación:
La solución a la ecuación diferencial para un intervalo de tiempo discreto se puede aproximar utilizando la siguiente expresión:
en la que \(\epsilon\) es una variable aleatoria que sigue una distribución normal estándar \(N(0,1)\).
import numpy as np
import matplotlib.pyplot as plt
def modelo_gbm(S0, mu, sigma, T, dt, seed=None):
"""
Genera una trayectoria de un Movimiento Browniano Geométrico con una semilla opcional para reproducibilidad.
Parámetros:
- S0: Precio inicial del activo.
- mu: Tasa de retorno esperada.
- sigma: Volatilidad del activo.
- T: Tiempo total de simulación.
- dt: Paso de tiempo de la simulación.
- seed: Semilla para el generador de números aleatorios (opcional).
Retorna:
- Una array de NumPy con la trayectoria del precio del activo.
"""
if seed is not None:
np.random.seed(seed) # Establecer la semilla
n = int(T / dt) # Número de pasos en el tiempo
t = np.linspace(0, T, n) # Vector de tiempos
W = np.random.standard_normal(size=n) # Incrementos del Movimiento Browniano
W = np.cumsum(W) * np.sqrt(dt) # Movimiento Browniano
X = (mu - 0.5 * sigma**2) * t + sigma * W
S = S0 * np.exp(X) # Trayectoria del Movimiento Browniano Geométrico
return S
# Parámetros del modelo
S0 = 100 # Precio inicial del activo
mu = 0.05 # Tasa de retorno esperada
sigma = 0.2 # Volatilidad
T = 1.0 # Tiempo total de simulación (e.g., 1 año)
dt = 0.01 # Paso de tiempo de la simulación
seed = 52 # Semilla para la reproducibilidad
# Generación de la trayectoria
trayectoria = modelo_gbm(S0, mu, sigma, T, dt, seed)
# Plot de la trayectoria
plt.plot(trayectoria)
plt.xlabel("Tiempo")
plt.ylabel("Precio del activo")
plt.title("Movimiento Browniano Geométrico")
plt.show()
100 trazas:#
import numpy as np
import matplotlib.pyplot as plt
def generar_gbm_multiples_trayectorias(
S0, mu, sigma, T, dt, num_trayectorias, seed=None
):
"""
Genera múltiples trayectorias de un Movimiento Browniano Geométrico.
Parámetros:
- S0: Precio inicial del activo.
- mu: Tasa de retorno esperada.
- sigma: Volatilidad del activo.
- T: Tiempo total de simulación.
- dt: Paso de tiempo de la simulación.
- num_trayectorias: Número de trayectorias a simular.
- seed: Semilla para el generador de números aleatorios (opcional).
Retorna:
- Un array de NumPy con las múltiples trayectorias del precio del activo.
"""
if seed is not None:
np.random.seed(seed) # Establecer la semilla
n = int(T / dt) # Número de pasos en el tiempo
t = np.linspace(0, T, n) # Vector de tiempos
S = np.zeros((n, num_trayectorias))
S[0] = S0
for i in range(1, n):
Z = np.random.standard_normal(num_trayectorias) # Genera variaciones aleatorias
S[i] = S[i - 1] * np.exp((mu - 0.5 * sigma**2) * dt + sigma * np.sqrt(dt) * Z)
return S
# Parámetros del modelo
S0 = 100 # Precio inicial del activo
mu = 0.05 # Tasa de retorno esperada
sigma = 0.2 # Volatilidad
T = 1.0 # Tiempo total de simulación (e.g., 1 año)
dt = 0.01 # Paso de tiempo de la simulación
num_trayectorias = 100 # Número de trayectorias a simular
seed = 52 # Semilla para la reproducibilidad
# Generación de las trayectorias
trayectorias = generar_gbm_multiples_trayectorias(
S0, mu, sigma, T, dt, num_trayectorias, seed
)
# Plot de las trayectorias
for i in range(num_trayectorias):
plt.plot(trayectorias[:, i], linewidth=1, alpha=0.5)
plt.xlabel("Tiempo")
plt.ylabel("Precio del activo")
plt.title("100 Trayectorias del Movimiento Browniano Geométrico")
plt.show()
Simulación con datos reales:#
Usar los siguientes archivos: Precio-ECO.csv y
Precio-ECO-mensual.csv
Pasos:
Cargar los datos: Utiliza pandas para cargar los precios del activo desde un archivo CSV.
Calcular \(\mu\) y \(\sigma\): Estos parámetros se calculan a partir de los datos históricos. La tasa de retorno esperada (\(\mu\)) se puede estimar como el promedio de las tasas de retorno logarítmicas diarias, y la volatilidad (\(\sigma\)) como la desviación estándar de estas tasas de retorno.
Simular el GBM: Con estos parámetros, puedes simular nuevas trayectorias de precios utilizando el GBM.
Simulación a partir de datos diarios:#
Análisis de los datos reales:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Leer el archivo CSV, ajustando el formato de los números
df = pd.read_csv("Precio-ECO.csv", delimiter=";")
df["Fecha"] = pd.to_datetime(df["Fecha"], format="%d/%m/%Y")
df["Precio"] = (
df["Precio"]
.str.replace(".", "", regex=False)
.str.replace(",", ".", regex=False)
.astype(float)
)
# Calcular los rendimientos logarítmicos para el gráfico
rendimientos_log = np.log(df["Precio"] / df["Precio"].shift(1))
# Crear figuras para los gráficos
fig, ax = plt.subplots(2, 1, figsize=(12, 8))
# Gráfico de los precios
ax[0].plot(df["Fecha"], df["Precio"], label="Precio", color="blue")
ax[0].set_title("Precio del Activo")
ax[0].set_xlabel("Fecha")
ax[0].set_ylabel("Precio")
ax[0].legend()
ax[0].grid(True)
# Gráfico de los rendimientos logarítmicos
ax[1].plot(
df["Fecha"], rendimientos_log, label="Rendimientos Logarítmicos", color="green"
)
ax[1].set_title("Rendimientos Logarítmicos")
ax[1].set_xlabel("Fecha")
ax[1].set_ylabel("Rendimiento")
ax[1].legend()
ax[1].grid(True)
plt.tight_layout()
plt.show()

Simulación de 180 días (T = 180) con saltos diarios (dt = 1)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Cargar los datos desde el archivo CSV, corrigiendo el formato de los números
df = pd.read_csv("Precio-ECO.csv", delimiter=";")
df["Fecha"] = pd.to_datetime(df["Fecha"], format="%d/%m/%Y")
df["Precio"] = (
df["Precio"]
.str.replace(".", "", regex=False)
.str.replace(",", ".", regex=False)
.astype(float)
)
# Calcular las tasas de retorno logarítmicas y sus parámetros
precios = df["Precio"].values
tasas_retorno_log = np.log(precios[1:] / precios[:-1])
mu = tasas_retorno_log.mean() # Promedio de la tasa de retorno logarítmica
sigma = tasas_retorno_log.std() # Volatilidad
# Función para simular múltiples trayectorias usando el modelo GBM
def simular_gbm(S0, mu, sigma, T, dt, num_trayectorias, seed=None):
"""
Simula múltiples trayectorias de un Movimiento Browniano Geométrico.
Parámetros:
- S0: Precio inicial del activo.
- mu: Tasa de retorno logarítmica media.
- sigma: Volatilidad del activo.
- T: Tiempo total de simulación.
- dt: Paso de tiempo de la simulación.
- num_trayectorias: Número de trayectorias a simular.
- seed: Semilla para el generador de números aleatorios (opcional).
Retorna:
- t: Vector de tiempos de simulación.
- S: Array con las trayectorias simuladas del precio del activo.
"""
if seed is not None:
np.random.seed(seed) # Establecer la semilla para reproducibilidad
n = int(T / dt) # Número de pasos en el tiempo
t = np.linspace(0, T, n)
S = np.zeros((n, num_trayectorias))
S[0] = S0
for i in range(1, n):
Z = np.random.standard_normal(num_trayectorias) # Genera variaciones aleatorias
S[i] = S[i - 1] * np.exp((mu - 0.5 * sigma**2) * dt + sigma * np.sqrt(dt) * Z)
return t, S
# Parámetros de la simulación
S0 = df["Precio"].iloc[-1] # Precio inicial: último precio conocido
T = 180 # Tiempo total de simulación
dt = 1 # Paso de tiempo
num_trayectorias = 100 # Número de trayectorias a simular
seed = 52 # Semilla para la reproducibilidad
# Simular las trayectorias y visualizar
t, trayectorias_simuladas = simular_gbm(S0, mu, sigma, T, dt, num_trayectorias, seed)
plt.figure(figsize=(10, 6))
for i in range(num_trayectorias):
plt.plot(t, trayectorias_simuladas[:, i], linewidth=1, alpha=0.5)
plt.xlabel("Tiempo (años)")
plt.ylabel("Precio del activo")
plt.title("Simulación GBM para Ecopetrol (saltos diarios por 180 días)")
plt.grid(True)
plt.show()
Simulación de 6 meses (T = 180) con saltos mensuales (dt = 1)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Cargar los datos desde el archivo CSV, corrigiendo el formato de los números
df = pd.read_csv("Precio-ECO.csv", delimiter=";")
df["Fecha"] = pd.to_datetime(df["Fecha"], format="%d/%m/%Y")
df["Precio"] = (
df["Precio"]
.str.replace(".", "", regex=False)
.str.replace(",", ".", regex=False)
.astype(float)
)
# Calcular las tasas de retorno logarítmicas y sus parámetros
precios = df["Precio"].values
tasas_retorno_log = np.log(precios[1:] / precios[:-1])
mu = tasas_retorno_log.mean() # Promedio de la tasa de retorno logarítmica
sigma = tasas_retorno_log.std() # Volatilidad
# Función para simular múltiples trayectorias usando el modelo GBM
def simular_gbm(S0, mu, sigma, T, dt, num_trayectorias, seed=None):
"""
Simula múltiples trayectorias de un Movimiento Browniano Geométrico.
Parámetros:
- S0: Precio inicial del activo.
- mu: Tasa de retorno logarítmica media.
- sigma: Volatilidad del activo.
- T: Tiempo total de simulación.
- dt: Paso de tiempo de la simulación.
- num_trayectorias: Número de trayectorias a simular.
- seed: Semilla para el generador de números aleatorios (opcional).
Retorna:
- t: Vector de tiempos de simulación.
- S: Array con las trayectorias simuladas del precio del activo.
"""
if seed is not None:
np.random.seed(seed) # Establecer la semilla para reproducibilidad
n = int(T / dt) # Número de pasos en el tiempo
t = np.linspace(0, T, n)
S = np.zeros((n, num_trayectorias))
S[0] = S0
for i in range(1, n):
Z = np.random.standard_normal(num_trayectorias) # Genera variaciones aleatorias
S[i] = S[i - 1] * np.exp((mu - 0.5 * sigma**2) * dt + sigma * np.sqrt(dt) * Z)
return t, S
# Parámetros de la simulación
S0 = df["Precio"].iloc[-1] # Precio inicial: último precio conocido
T = 180 # Tiempo total de simulación
dt = 30 # Paso de tiempo
num_trayectorias = 100 # Número de trayectorias a simular
seed = 52 # Semilla para la reproducibilidad
# Simular las trayectorias y visualizar
t, trayectorias_simuladas = simular_gbm(S0, mu, sigma, T, dt, num_trayectorias, seed)
plt.figure(figsize=(10, 6))
for i in range(num_trayectorias):
plt.plot(t, trayectorias_simuladas[:, i], linewidth=1, alpha=0.5)
plt.xlabel("Tiempo (años)")
plt.ylabel("Precio del activo")
plt.title("Simulación GBM para Ecopetrol (saltos mensuales por 6 meses)")
plt.grid(True)
plt.show()
Simulación a partir de datos mensuales:#
Simulación de 6 meses (T = 6) con saltos mensuales (dt = 1)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Cargar los datos desde el archivo CSV, corrigiendo el formato de los números
df = pd.read_csv("Precio-ECO-mensual.csv", delimiter=";")
df["Fecha"] = pd.to_datetime(df["Fecha"], format="%d/%m/%Y")
df["Precio"] = (
df["Precio"]
.str.replace(".", "", regex=False)
.str.replace(",", ".", regex=False)
.astype(float)
)
# Calcular las tasas de retorno logarítmicas y sus parámetros
precios = df["Precio"].values
tasas_retorno_log = np.log(precios[1:] / precios[:-1])
mu = tasas_retorno_log.mean() # Promedio de la tasa de retorno logarítmica
sigma = tasas_retorno_log.std() # Volatilidad
# Función para simular múltiples trayectorias usando el modelo GBM
def simular_gbm(S0, mu, sigma, T, dt, num_trayectorias, seed=None):
"""
Simula múltiples trayectorias de un Movimiento Browniano Geométrico.
Parámetros:
- S0: Precio inicial del activo.
- mu: Tasa de retorno logarítmica media.
- sigma: Volatilidad del activo.
- T: Tiempo total de simulación.
- dt: Paso de tiempo de la simulación.
- num_trayectorias: Número de trayectorias a simular.
- seed: Semilla para el generador de números aleatorios (opcional).
Retorna:
- t: Vector de tiempos de simulación.
- S: Array con las trayectorias simuladas del precio del activo.
"""
if seed is not None:
np.random.seed(seed) # Establecer la semilla para reproducibilidad
n = int(T / dt) # Número de pasos en el tiempo
t = np.linspace(0, T, n)
S = np.zeros((n, num_trayectorias))
S[0] = S0
for i in range(1, n):
Z = np.random.standard_normal(num_trayectorias) # Genera variaciones aleatorias
S[i] = S[i - 1] * np.exp((mu - 0.5 * sigma**2) * dt + sigma * np.sqrt(dt) * Z)
return t, S
# Parámetros de la simulación
S0 = df["Precio"].iloc[-1] # Precio inicial: último precio conocido
T = 6 # Tiempo total de simulación
dt = 1 # Paso de tiempo
num_trayectorias = 100 # Número de trayectorias a simular
seed = 52 # Semilla para la reproducibilidad
# Simular las trayectorias y visualizar
t, trayectorias_simuladas = simular_gbm(S0, mu, sigma, T, dt, num_trayectorias, seed)
plt.figure(figsize=(10, 6))
for i in range(num_trayectorias):
plt.plot(t, trayectorias_simuladas[:, i], linewidth=1, alpha=0.5)
plt.xlabel("Tiempo (años)")
plt.ylabel("Precio del activo")
plt.title("Simulación GBM para Ecopetrol (saltos mensuales por 6 meses)")
plt.grid(True)
plt.show()
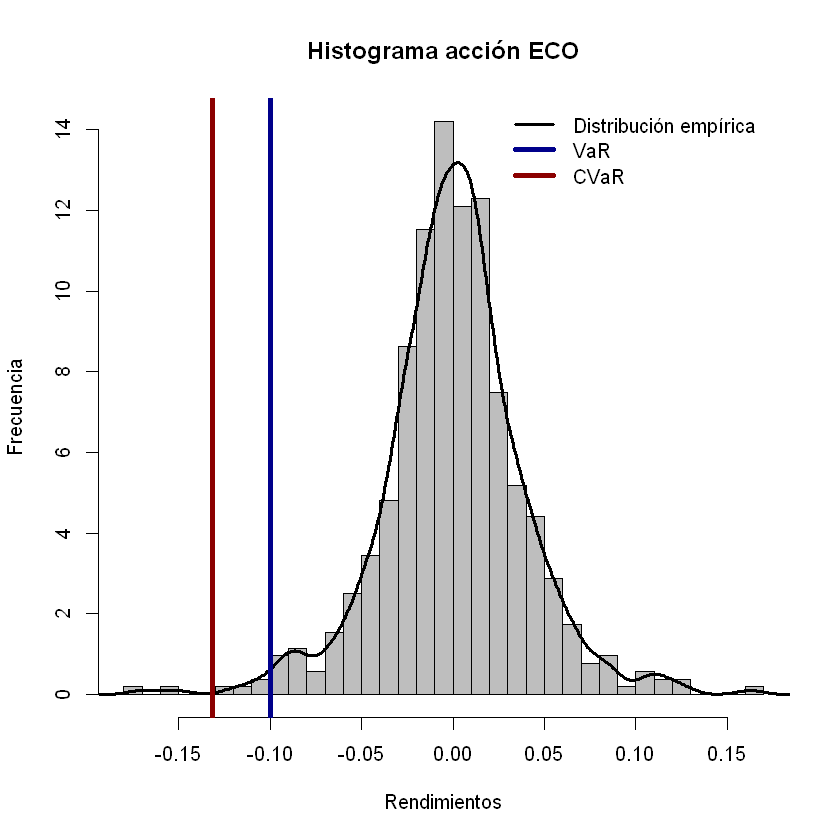
Prueba de la Simulación Monte Carlo:#
import numpy as np
import matplotlib.pyplot as plt
# Parámetros del GBM
S0 = 100 # Precio inicial
mu = 0.05 # Tasa de retorno esperada
sigma = 0.2 # Volatilidad
T = 1.0 # Tiempo total de simulación (1 año)
dt = 1 / 252 # Paso de tiempo (suponiendo 252 días de trading al año)
def simular_gbm(S0, mu, sigma, T, dt, num_simulaciones):
n = int(T / dt) # Número de pasos en el tiempo
precios_finales = np.zeros(num_simulaciones)
for i in range(num_simulaciones):
Z = np.random.standard_normal(n) # Genera variaciones aleatorias
precios = S0 * np.exp(
np.cumsum((mu - 0.5 * sigma**2) * dt + sigma * np.sqrt(dt) * Z)
)
precios_finales[i] = precios[-1] # Almacenar el precio final de cada simulación
return precios_finales.mean() # Devolver el promedio de los precios finales
# Realizar simulaciones aumentando gradualmente el número de simulaciones
num_simulaciones_prueba = [10, 50, 100, 500, 1000, 2000, 5000, 10000, 20000, 50000]
promedios = []
for num in num_simulaciones_prueba:
promedio = simular_gbm(S0, mu, sigma, T, dt, num)
promedios.append(promedio)
# Graficar cómo se estabiliza el promedio de los precios finales
plt.figure(figsize=(10, 6))
plt.plot(num_simulaciones_prueba, promedios, marker="o")
plt.xscale("log") # Escala logarítmica para el eje X
plt.xlabel("Número de Simulaciones")
plt.ylabel("Promedio del Precio Final")
plt.title("Estabilización del promedio con el aumento de Simulaciones Monte Carlo")
plt.grid(True)
plt.show()