Árboles de decisión para series de tiempo

import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
import matplotlib.pyplot as plt
import scipy.stats as stats
from sklearn.model_selection import RandomizedSearchCV

import warnings

# Suprimir todas las advertencias
warnings.filterwarnings("ignore")

# Cargar los datos omitiendo la primera fila como encabezado y asignando nombres a las columnas
data = pd.read_csv("../Irradiance_mensual.csv", skiprows=1, header=None, names=['Fecha', 'Irradiancia'])

# Convertir la columna 'Fecha' a datetime
data['Fecha'] = pd.to_datetime(data['Fecha'], format='%Y-%m')

# Set 'Fecha' as the index
data.set_index('Fecha', inplace=True)

# Cantidad de datos
n = data.shape[0]
print("Cantidad de datos:", n)

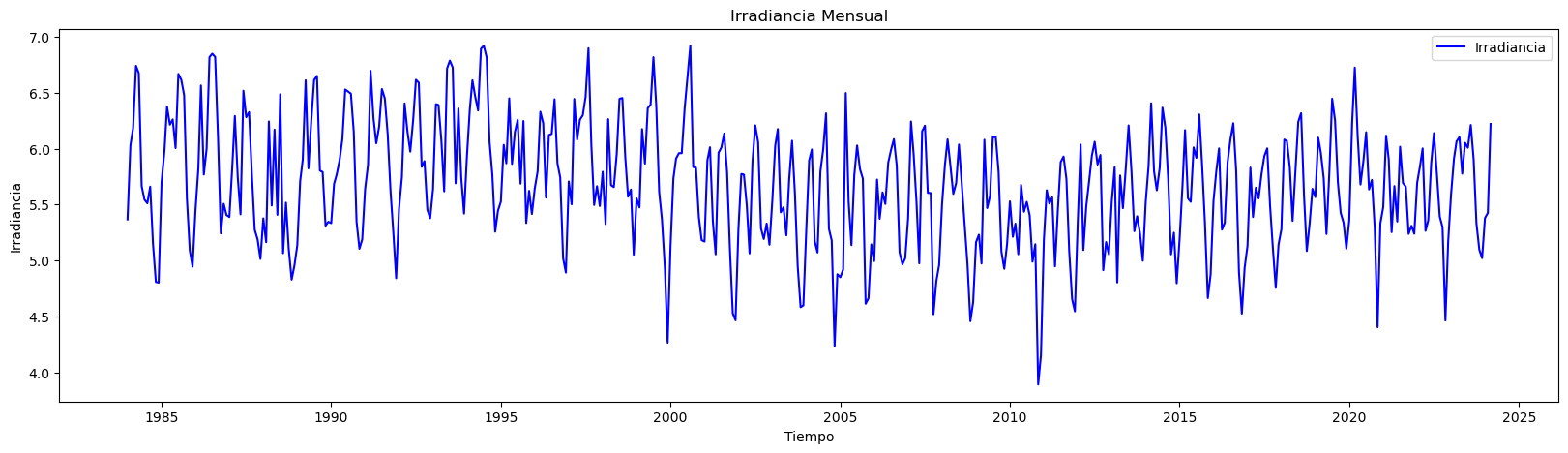
plt.figure(figsize=(20, 5))  # Establecer el tamaño del gráfico
plt.plot(data.index, data['Irradiancia'], label='Irradiancia', color='blue')  # Dibujar los datos reales
plt.title('Irradiancia Mensual')  # Título del gráfico
plt.xlabel('Tiempo')  # Etiqueta del eje X
plt.ylabel('Irradiancia')  # Etiqueta del eje Y
plt.legend()  # Añadir leyenda para identificar las líneas
plt.show()

Cantidad de datos: 483

Conjunto de Train y Test

# Definir características (X) y objetivo (y)
X = data[["Irradiancia"]]  # Usar la irradiancia como característica
y = data["Irradiancia"]  # Usar la irradiancia también como objetivo

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=False)

Árboles de decisión para regresión:

# Crear el modelo de árbol de decisión
tree_regressor = DecisionTreeRegressor(random_state=34)

# Entrenar el modelo en el conjunto de entrenamiento
tree_regressor.fit(X_train, y_train)

DecisionTreeRegressor(random_state=34)

Evaluación del modelo:

Sobre el conjunto de Train:

# Predicciones en el conjunto de prueba
y_pred_train = tree_regressor.predict(X_train)

# Calcular MAE
mae_train = mean_absolute_error(y_train, y_pred_train)

# Calcular MSE
mse_train = mean_squared_error(y_train, y_pred_train)

# Calcular RMSE
rmse_train = np.sqrt(mse_train)

# Calcular R² Score
r2_train = r2_score(y_train, y_pred_train)

# Mostar métricas
print("Métricas en el conjunto de entrenamiento:")
print("Mean Absolute Error (MAE):", mae_train)
print("Mean Squared Error (MSE):", mse_train)
print("Root Mean Squared Error (RMSE):", rmse_train)
print("R² Score:", r2_train)

Métricas en el conjunto de entrenamiento:
Mean Absolute Error (MAE): 0.0
Mean Squared Error (MSE): 0.0
Root Mean Squared Error (RMSE): 0.0
R² Score: 1.0

Sobre el conjunto de Test:

# Predicciones en el conjunto de prueba
y_pred = tree_regressor.predict(X_test)

# Calcular MAE
mae = mean_absolute_error(y_test, y_pred)

# Calcular MSE
mse = mean_squared_error(y_test, y_pred)

# Calcular RMSE
rmse = np.sqrt(mse)

# Calcular R² Score
r2 = r2_score(y_test, y_pred)

# Mostrar las métricas
print("Métricas en el conjunto de entrenamiento:")
print(f"Mean Absolute Error (MAE): {mae}")
print(f"Mean Squared Error (MSE): {mse}")
print(f"Root Mean Squared Error (RMSE): {rmse}")
print(f"R² Score: {r2}")

Métricas en el conjunto de entrenamiento:
Mean Absolute Error (MAE): 0.003318427500582964
Mean Squared Error (MSE): 5.726579999023996e-05
Root Mean Squared Error (RMSE): 0.007567416995926679
R² Score: 0.9997066910209671

# Gráfica de resultados
plt.figure(figsize=(14, 7))
plt.plot(y_test.index, y_test.values, label="Test", color="green")
plt.plot(y_test.index, y_pred, label="Predicted", linestyle="--", color="red")
plt.title("Ajuste modelo árboles de decisión")
plt.xlabel("Fecha")
plt.ylabel("Irradiancia")
plt.legend()
plt.show()

Análisis de residuales:

# Hacer predicciones en el conjunto de entrenamiento
y_pred_train = tree_regressor.predict(X_train)

# Calcular los residuales sobre el conjunto de entrenamiento
residuals_train = y_train - y_pred_train

# Configuración de la figura para los subplots
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(14, 6))

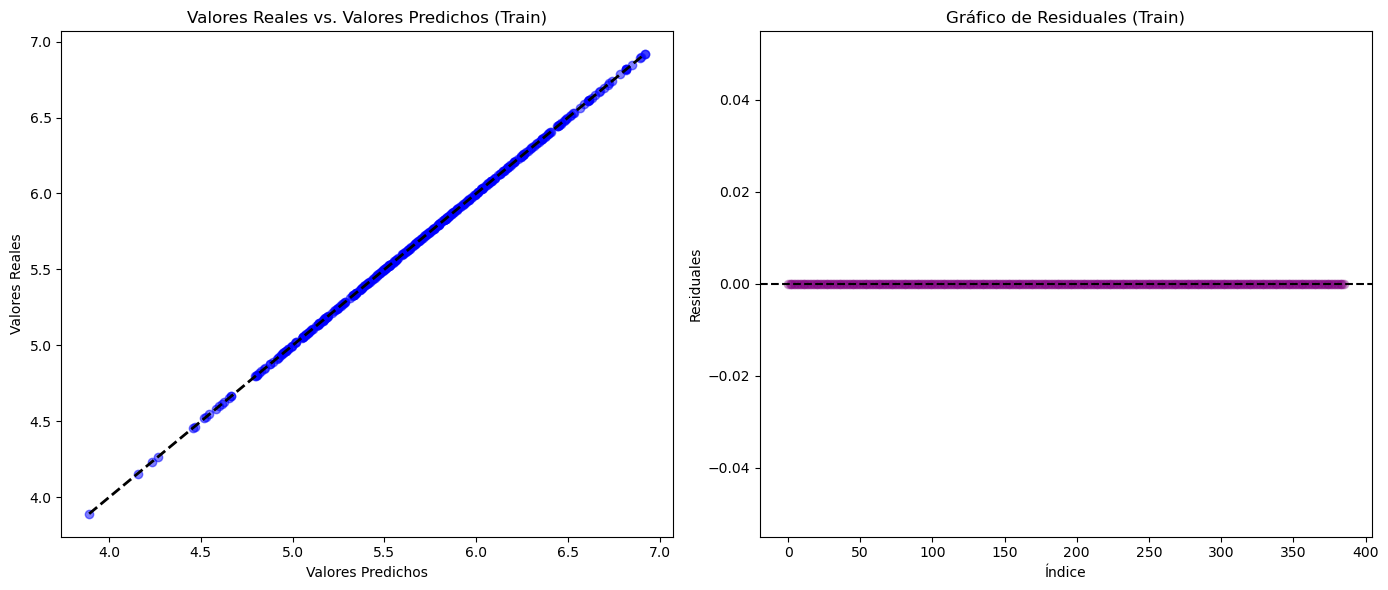
# Gráfico de valores predichos vs. valores reales
axs[0].scatter(y_pred_train, y_train, color="blue", alpha=0.5)
axs[0].plot(
    [y_train.min(), y_train.max()], [y_train.min(), y_train.max()], "k--", lw=2
)  # Línea diagonal ideal
axs[0].set_title("Valores Reales vs. Valores Predichos (Train)")
axs[0].set_xlabel("Valores Predichos")
axs[0].set_ylabel("Valores Reales")

# Gráfico de residuales
axs[1].scatter(y_train.index, residuals_train, color="purple", alpha=0.3)
axs[1].axhline(y=0, color="black", linestyle="--")  # Línea en y=0 para referencia
axs[1].set_title("Gráfico de Residuales (Train)")
axs[1].set_xlabel("Tiempo")
axs[1].set_ylabel("Residuales")

# Mejorar el layout para evitar solapamientos
plt.tight_layout()

# Mostrar la figura
plt.show()

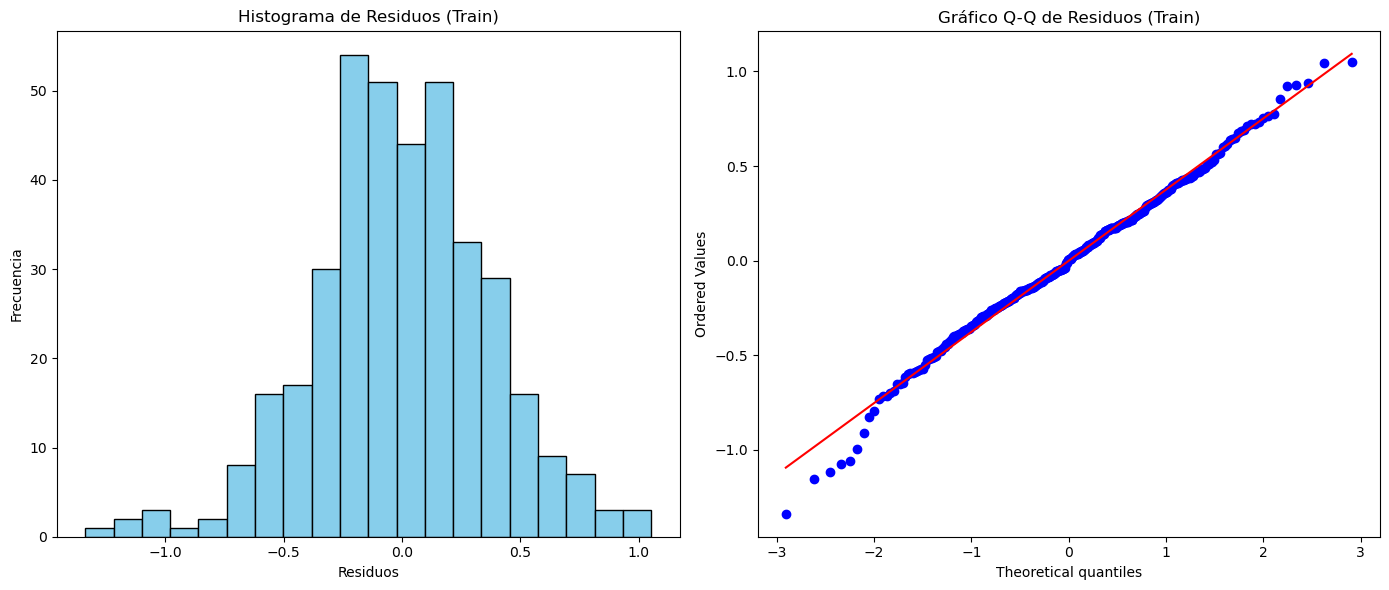
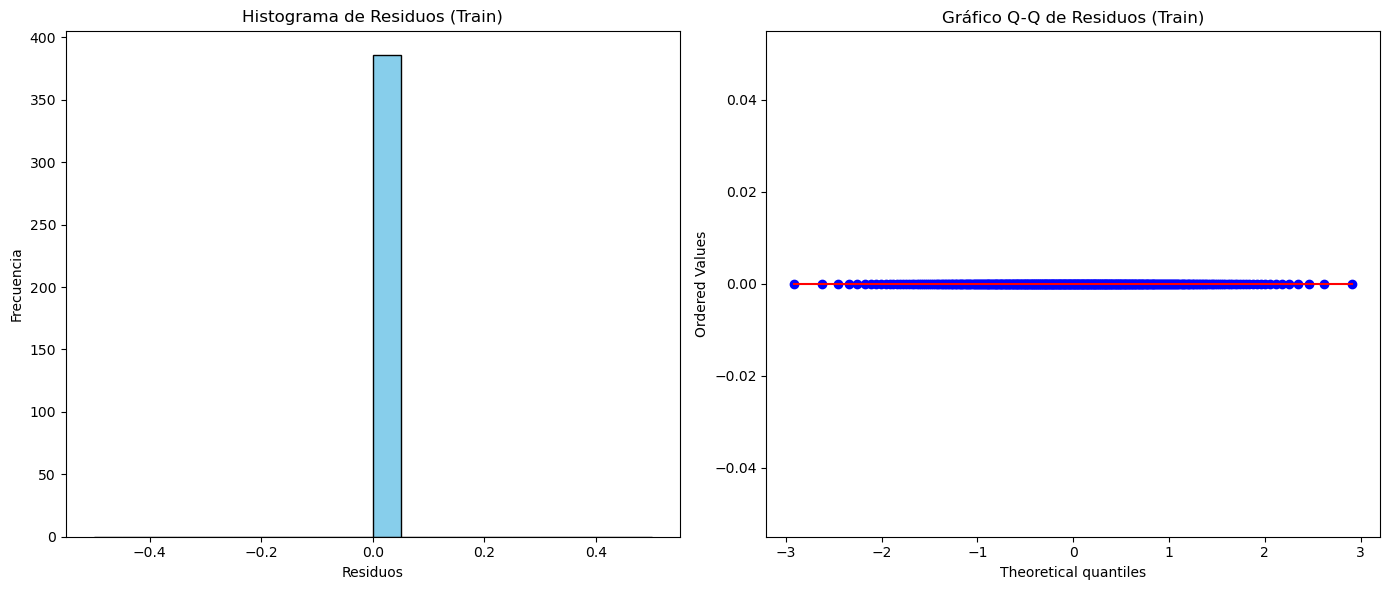
# Visualización del histograma de los residuos
plt.figure(figsize=(14, 6))

plt.subplot(1, 2, 1)
plt.hist(residuals_train, bins=20, color="skyblue", edgecolor="black")
plt.title("Histograma de Residuos (Train)")
plt.xlabel("Residuos")
plt.ylabel("Frecuencia")

# Visualización del gráfico Q-Q de los residuos
plt.subplot(1, 2, 2)
stats.probplot(residuals_train, dist="norm", plot=plt)
plt.title("Gráfico Q-Q de Residuos (Train)")

# Ajustar el diseño de la figura
plt.tight_layout()

# Mostrar la figura
plt.show()

Predicciones fuera de la muestra:

# Tomar el último valor de X_test como punto de partida para las predicciones fuera de muestra
last_X = X_test.iloc[-1].values.reshape(1, -1)


# Número de pasos adelante para predecir
n_steps_ahead = 24

# Array para almacenar las predicciones fuera de muestra
predictions_out_of_sample = []

for _ in range(n_steps_ahead):
    # Hacer la predicción usando el último valor de X
    pred = tree_regressor.predict(last_X)

    # Guardar la predicción
    predictions_out_of_sample.append(pred[0])

    # Crear la nueva entrada para la siguiente predicción
    # Aquí se utiliza la predicción actual como la siguiente entrada
    last_X = np.array(pred).reshape(1, -1)

# Crear un rango de fechas para las predicciones fuera de muestra
dates_out_of_sample = pd.date_range(
    start=y_test.index[-1], periods=n_steps_ahead + 1, freq="M"
)[1:]

# Graficar las predicciones fuera de muestra
plt.figure(figsize=(10, 6))
plt.plot(y_test.index, y_test, label="Datos Reales (Test)")
plt.plot(
    dates_out_of_sample,
    predictions_out_of_sample,
    label="Predicciones Fuera de Muestra",
    color="red",
    linestyle="--",
)
plt.title("Predicciones Fuera de Muestra con Árbol de Decisión")
plt.xlabel("Fecha")
plt.ylabel("Valores Predichos")
plt.legend()
plt.show()

Optimización de Hiperparámetros:

# Crear el modelo de árbol de decisión
tree_regressor = DecisionTreeRegressor(random_state=34)

# Definir el espacio de hiperparámetros
param_dist = {
    "max_depth": list(np.arange(1, 20)),  # Profundidad máxima del árbol
    "min_samples_split": np.arange(2, 20),  # Mínimo número de muestras para dividir un nodo
    "min_samples_leaf": np.arange(5, 20),  # Mínimo número de muestras en una hoja
    "max_features": [None, "auto", "sqrt", "log2"],  # Número de características a considerar para la mejor división
    "max_leaf_nodes": [None] + list(np.arange(2, 100)),  # Número máximo de nodos hoja
}

# Configurar RandomizedSearchCV
random_search = RandomizedSearchCV(
    estimator=tree_regressor,
    param_distributions=param_dist,
    n_iter=300,  # Número de combinaciones aleatorias a evaluar
    scoring="neg_mean_squared_error",  # Usar MSE negativo como métrica de scoring
    cv=5,  # Validación cruzada con 5 pliegues
    verbose=2,
    random_state=34,
    n_jobs=-1,  # Usar todos los núcleos disponibles
)

# Ajustar RandomizedSearchCV al conjunto de entrenamiento
random_search.fit(X_train, y_train)

Fitting 5 folds for each of 300 candidates, totalling 1500 fits

RandomizedSearchCV(cv=5, estimator=DecisionTreeRegressor(random_state=34),
                   n_iter=300, n_jobs=-1,
                   param_distributions={'max_depth': [1, 2, 3, 4, 5, 6, 7, 8, 9,
                                                      10, 11, 12, 13, 14, 15,
                                                      16, 17, 18, 19],
                                        'max_features': [None, 'auto', 'sqrt',
                                                         'log2'],
                                        'max_leaf_nodes': [None, 2, 3, 4, 5, 6,
                                                           7, 8, 9, 10, 11, 12,
                                                           13, 14, 15, 16, 17,
                                                           18, 19, 20, 21, 22,
                                                           23, 24, 25, 26, 27,
                                                           28, 29, 30, ...],
                                        'min_samples_leaf': array([ 5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]),
                                        'min_samples_split': array([ 2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18,
       19])},
                   random_state=34, scoring='neg_mean_squared_error',
                   verbose=2)

# Obtener los mejores hiperparámetros
best_params = random_search.best_params_
best_score = random_search.best_score_

print(f"Mejores hiperparámetros: {best_params}")

Mejores hiperparámetros: {'min_samples_split': 3, 'min_samples_leaf': 5, 'max_leaf_nodes': 83, 'max_features': 'sqrt', 'max_depth': 14}

# Mejor modelo encontrado:
best_model = random_search.best_estimator_

# Predicciones en el conjunto de prueba
y_pred_train = best_model.predict(X_train)

# Calcular MAE
mae_train = mean_absolute_error(y_train, y_pred_train)

# Calcular MSE
mse_train = mean_squared_error(y_train, y_pred_train)

# Calcular RMSE
rmse_train = np.sqrt(mse_train)

# Calcular R² Score
r2_train = r2_score(y_train, y_pred_train)

# Mostar métricas
print("Métricas en el conjunto de entrenamiento:")
print("Mean Absolute Error (MAE):", mae_train)
print("Mean Squared Error (MSE):", mse_train)
print("Root Mean Squared Error (RMSE):", rmse_train)
print("R² Score:", r2_train)

Métricas en el conjunto de entrenamiento:
Mean Absolute Error (MAE): 0.010106275359833619
Mean Squared Error (MSE): 0.0005711430968164161
Root Mean Squared Error (RMSE): 0.023898600310821888
R² Score: 0.9981737629051306

# Predicciones en el conjunto de prueba
y_pred = best_model.predict(X_test)

# Calcular MAE
mae = mean_absolute_error(y_test, y_pred)

# Calcular MSE
mse = mean_squared_error(y_test, y_pred)

# Calcular RMSE
rmse = np.sqrt(mse)

# Calcular R² Score
r2 = r2_score(y_test, y_pred)

# Mostrar las métricas
print("Métricas en el conjunto de entrenamiento:")
print(f"Mean Absolute Error (MAE): {mae}")
print(f"Mean Squared Error (MSE): {mse}")
print(f"Root Mean Squared Error (RMSE): {rmse}")
print(f"R² Score: {r2}")

Métricas en el conjunto de entrenamiento:
Mean Absolute Error (MAE): 0.011398115305865372
Mean Squared Error (MSE): 0.00060460039986064
Root Mean Squared Error (RMSE): 0.02458862338278904
R² Score: 0.996903304834016

# Gráfica de resultados
plt.figure(figsize=(14, 7))
plt.plot(y_test.index, y_test.values, label="Test", color="green")
plt.plot(y_test.index, y_pred, label="Predicted", linestyle="--", color="red")
plt.title("Ajuste modelo árboles de decisión")
plt.xlabel("Fecha")
plt.ylabel("Irradiancia")
plt.legend()
plt.show()

Residuales:

# Hacer predicciones en el conjunto de entrenamiento
y_pred_train = best_model.predict(X_train)

# Calcular los residuales sobre el conjunto de entrenamiento
residuals_train = y_train - y_pred_train

# Configuración de la figura para los subplots
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(14, 6))

# Gráfico de valores predichos vs. valores reales
axs[0].scatter(y_pred_train, y_train, color="blue", alpha=0.5)
axs[0].plot(
    [y_train.min(), y_train.max()], [y_train.min(), y_train.max()], "k--", lw=2
)  # Línea diagonal ideal
axs[0].set_title("Valores Reales vs. Valores Predichos (Train)")
axs[0].set_xlabel("Valores Predichos")
axs[0].set_ylabel("Valores Reales")

# Gráfico de residuales
axs[1].scatter(y_train.index, residuals_train, color="purple", alpha=0.3)
axs[1].axhline(y=0, color="black", linestyle="--")  # Línea en y=0 para referencia
axs[1].set_title("Gráfico de Residuales (Train)")
axs[1].set_xlabel("Tiempo")
axs[1].set_ylabel("Residuales")

# Mejorar el layout para evitar solapamientos
plt.tight_layout()

# Mostrar la figura
plt.show()

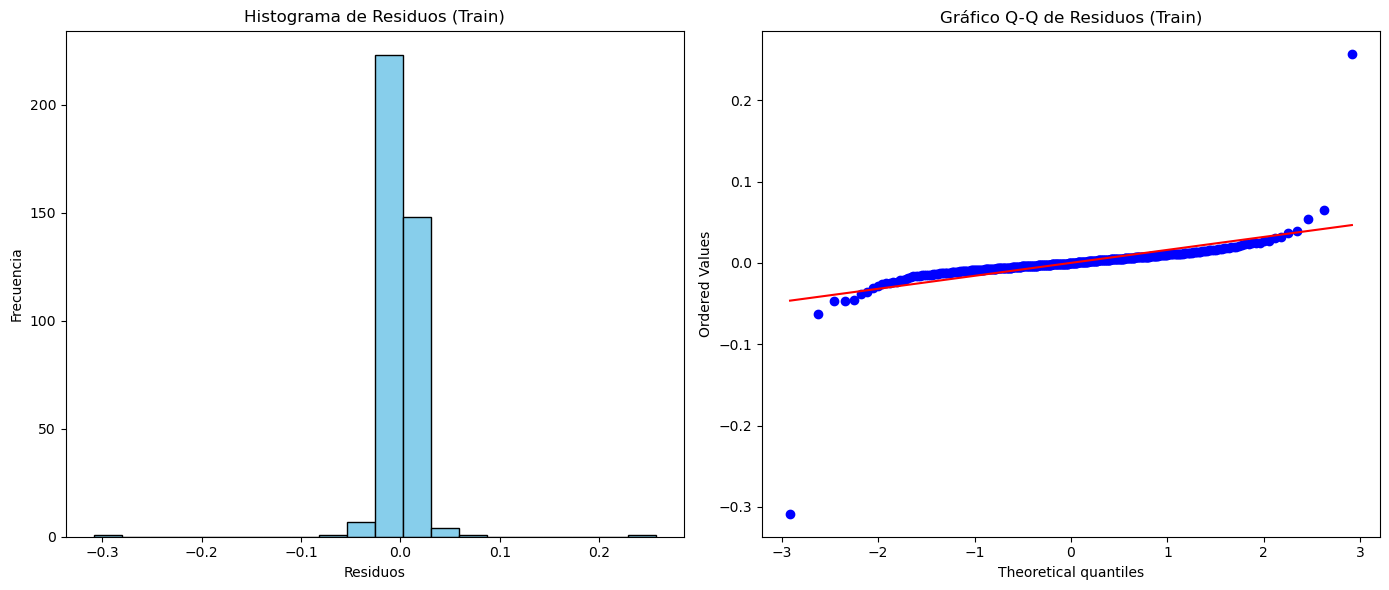
# Visualización del histograma de los residuos
plt.figure(figsize=(14, 6))

plt.subplot(1, 2, 1)
plt.hist(residuals_train, bins=20, color="skyblue", edgecolor="black")
plt.title("Histograma de Residuos (Train)")
plt.xlabel("Residuos")
plt.ylabel("Frecuencia")

# Visualización del gráfico Q-Q de los residuos
plt.subplot(1, 2, 2)
stats.probplot(residuals_train, dist="norm", plot=plt)
plt.title("Gráfico Q-Q de Residuos (Train)")

# Ajustar el diseño de la figura
plt.tight_layout()

# Mostrar la figura
plt.show()

Predicciones fuera de la muestra:

# Tomar el último valor de X_test como punto de partida para las predicciones fuera de muestra
last_X = X_test.iloc[-1].values.reshape(1, -1)


# Número de pasos adelante para predecir
n_steps_ahead = 12 * 5

# Array para almacenar las predicciones fuera de muestra
predictions_out_of_sample = []

for _ in range(n_steps_ahead):
    # Hacer la predicción usando el último valor de X
    pred = best_model.predict(last_X)

    # Guardar la predicción
    predictions_out_of_sample.append(pred[0])

    # Crear la nueva entrada para la siguiente predicción
    # Aquí se utiliza la predicción actual como la siguiente entrada
    last_X = np.array(pred).reshape(1, -1)

# Crear un rango de fechas para las predicciones fuera de muestra
dates_out_of_sample = pd.date_range(
    start=y_test.index[-1], periods=n_steps_ahead + 1, freq="M"
)[1:]

# Graficar las predicciones fuera de muestra
plt.figure(figsize=(10, 6))
plt.plot(y_test.index, y_test, label="Datos Reales (Test)")
plt.plot(
    dates_out_of_sample,
    predictions_out_of_sample,
    label="Predicciones Fuera de Muestra",
    color="red",
    linestyle="--",
)
plt.title("Predicciones Fuera de Muestra con Árbol de Decisión")
plt.xlabel("Fecha")
plt.ylabel("Valores Predichos")
plt.legend()
plt.show()

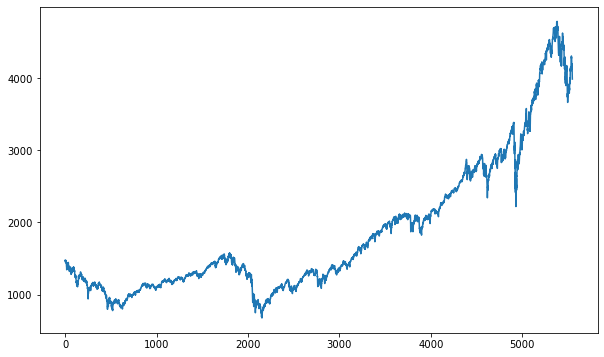
Lags de la serie de tiempo como variables de entrada:

Los árboles de decisión son muy sensibles a los datos; si se modifican los lags, los resultados pueden variar significativamente.

# Crear características de lags
n_lags = 7  # Número de lags que deseas utilizar

data_lags = data.copy()
for lag in range(1, n_lags + 1):
    data_lags[f"Irradiancia_Lag_{lag}"] = data["Irradiancia"].shift(lag)

# Eliminar las filas con valores NaN resultantes de los lags
data_lags.dropna(inplace=True)
print(data_lags.head())

            Irradiancia  Irradiancia_Lag_1  Irradiancia_Lag_2  Fecha
1984-08-01     5.511290           5.544516           5.665000
1984-09-01     5.660333           5.511290           5.544516
1984-10-01     5.150323           5.660333           5.511290
1984-11-01     4.808667           5.150323           5.660333
1984-12-01     4.802258           4.808667           5.150323

            Irradiancia_Lag_3  Irradiancia_Lag_4  Irradiancia_Lag_5  Fecha
1984-08-01           6.674194           6.739667           6.182903
1984-09-01           5.665000           6.674194           6.739667
1984-10-01           5.544516           5.665000           6.674194
1984-11-01           5.511290           5.544516           5.665000
1984-12-01           5.660333           5.511290           5.544516

            Irradiancia_Lag_6  Irradiancia_Lag_7
Fecha
1984-08-01           6.030690           5.367742
1984-09-01           6.182903           6.030690
1984-10-01           6.739667           6.182903
1984-11-01           6.674194           6.739667
1984-12-01           5.665000           6.674194

# Separar características (X) y la variable objetivo (y)
X_lags = data_lags.drop(columns=["Irradiancia"])
y_lags = data_lags["Irradiancia"]

X_train_lags, X_test_lags, y_train_lags, y_test_lags = train_test_split(
    X_lags, y_lags, test_size=0.2, shuffle=False, random_state=34
)

# Crear el modelo de árbol de decisión
tree_regressor_lags = DecisionTreeRegressor(random_state=34)

# Definir el espacio de hiperparámetros
param_dist = {
    "max_depth": list(np.arange(1, 20)),
    "min_samples_split": np.arange(2, 20),
    "min_samples_leaf": np.arange(5, 20),
    "max_features": [None, "auto", "sqrt", "log2"],
    "max_leaf_nodes": [None] + list(np.arange(2, 100)),
}

# Configurar RandomizedSearchCV
random_search_lags = RandomizedSearchCV(
    estimator=tree_regressor_lags,
    param_distributions=param_dist,
    n_iter=300,
    scoring="neg_mean_squared_error",
    cv=5,
    verbose=2,
    random_state=42,
    n_jobs=-1,
)

# Ajustar RandomizedSearchCV al conjunto de entrenamiento
random_search_lags.fit(X_train_lags, y_train_lags)

# Mejor modelo encontrado:
best_model_lags = random_search_lags.best_estimator_

# Obtener los mejores hiperparámetros
best_params_lags = random_search_lags.best_params_
print(f"Mejores hiperparámetros: {best_params_lags}")

Fitting 5 folds for each of 300 candidates, totalling 1500 fits
Mejores hiperparámetros: {'min_samples_split': 11, 'min_samples_leaf': 17, 'max_leaf_nodes': 86, 'max_features': None, 'max_depth': 19}

# Predicciones en el conjunto de prueba
y_pred_train = best_model_lags.predict(X_train_lags)

# Calcular MAE
mae_train = mean_absolute_error(y_train_lags, y_pred_train)

# Calcular MSE
mse_train = mean_squared_error(y_train_lags, y_pred_train)

# Calcular RMSE
rmse_train = np.sqrt(mse_train)

# Calcular R² Score
r2_train = r2_score(y_train_lags, y_pred_train)

# Mostar métricas
print("Métricas en el conjunto de entrenamiento:")
print("Mean Absolute Error (MAE):", mae_train)
print("Mean Squared Error (MSE):", mse_train)
print("Root Mean Squared Error (RMSE):", rmse_train)
print("R² Score:", r2_train)

Métricas en el conjunto de entrenamiento:
Mean Absolute Error (MAE): 0.29360416854625876
Mean Squared Error (MSE): 0.14067565958623438
Root Mean Squared Error (RMSE): 0.37506754003277115
R² Score: 0.5479854699681128

# Predicciones en el conjunto de prueba
y_pred_lags = best_model_lags.predict(X_test_lags)

# Calcular MAE
mae = mean_absolute_error(y_test_lags, y_pred_lags)

# Calcular MSE
mse = mean_squared_error(y_test_lags, y_pred_lags)

# Calcular RMSE
rmse = np.sqrt(mse)

# Calcular R² Score
r2 = r2_score(y_test_lags, y_pred_lags)

# Mostrar las métricas
print("Métricas en el conjunto de entrenamiento:")
print(f"Mean Absolute Error (MAE): {mae}")
print(f"Mean Squared Error (MSE): {mse}")
print(f"Root Mean Squared Error (RMSE): {rmse}")
print(f"R² Score: {r2}")

Métricas en el conjunto de entrenamiento:
Mean Absolute Error (MAE): 0.30917753360149003
Mean Squared Error (MSE): 0.16115155223053157
Root Mean Squared Error (RMSE): 0.40143685958134384
R² Score: 0.17695088832056238

# Gráfica de resultados
plt.figure(figsize=(14, 7))
plt.plot(y_test[1:].index, y_test[1:].values, label="Test", color="green")
plt.plot(y_test_lags.index, y_pred_lags, label="Predicted", linestyle="--", color="red")
plt.title("Ajuste modelo árboles de decisión")
plt.xlabel("Fecha")
plt.ylabel("Irradiancia")
plt.legend()
plt.show()

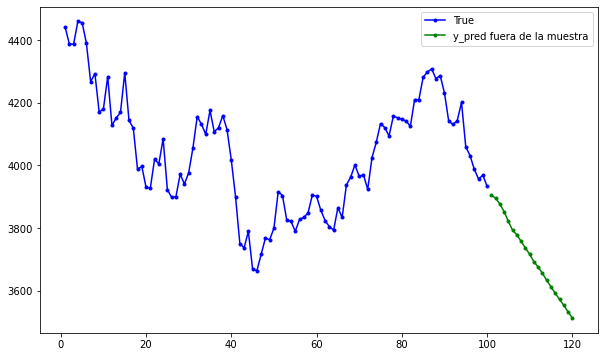
# Preparar el punto de partida (última fila de X_test)
last_X_lags = X_test_lags.iloc[-1].values.reshape(1, -1)

# Número de pasos adelante para predecir
n_steps_ahead = 12 * 5

# Lista para almacenar las predicciones fuera de muestra
predictions_out_of_sample = []

for _ in range(n_steps_ahead):
    # Hacer la predicción usando el último valor de X
    pred = best_model_lags.predict(last_X_lags)

    # Guardar la predicción
    predictions_out_of_sample.append(pred[0])

    # Crear la nueva entrada para la siguiente predicción utilizando los lags
    new_X = np.roll(last_X_lags, shift=-1)  # Desplazar valores
    new_X[0, -n_lags:] = pred  # Actualizar con la nueva predicción
    last_X_lags = new_X.reshape(1, -1)  # Reajustar la forma

# Crear un rango de fechas para las predicciones fuera de muestra
dates_out_of_sample = pd.date_range(
    start=y_test.index[-1], periods=n_steps_ahead + 1, freq="M"
)[1:]

# Graficar las predicciones fuera de muestra
plt.figure(figsize=(10, 6))
plt.plot(y_test.index, y_test, label="Datos Reales (Test)")
plt.plot(
    dates_out_of_sample,
    predictions_out_of_sample,
    label="Predicciones Fuera de Muestra",
    color="red",
    linestyle="--",
)
plt.title("Predicciones fuera de muestra con árbol de decisión (con Lags)")
plt.xlabel("Fecha")
plt.ylabel("Valores Predichos")
plt.legend()
plt.show()

Residuales:

# Hacer predicciones en el conjunto de entrenamiento con el mejor modelo
y_pred_train = best_model_lags.predict(X_train_lags)

# Calcular los residuales en el conjunto de entrenamiento
residuals_train = y_train_lags - y_pred_train

# Configuración de la figura para los subplots
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(14, 6))

# Gráfico de valores predichos vs. valores reales
axs[0].scatter(y_pred_train, y_train[n_lags - 1 :], color="blue", alpha=0.5)
axs[0].plot(
    [y_train.min(), y_train.max()], [y_train.min(), y_train.max()], "k--", lw=2
)  # Línea diagonal ideal
axs[0].set_title("Valores Reales vs. Valores Predichos (Train)")
axs[0].set_xlabel("Valores Predichos")
axs[0].set_ylabel("Valores Reales")

# Gráfico de residuales
axs[1].scatter(y_train.index, residuals_train, color="purple", alpha=0.3)
axs[1].axhline(y=0, color="black", linestyle="--")  # Línea en y=0 para referencia
axs[1].set_title("Gráfico de Residuales (Train)")
axs[1].set_xlabel("Tiempo")
axs[1].set_ylabel("Residuales")

# Mejorar el layout para evitar solapamientos
plt.tight_layout()
plt.show()

# Visualización del histograma de los residuos
plt.figure(figsize=(14, 6))

plt.subplot(1, 2, 1)
plt.hist(residuals_train, bins=20, color="skyblue", edgecolor="black")
plt.title("Histograma de Residuos (Train)")
plt.xlabel("Residuos")
plt.ylabel("Frecuencia")

# Visualización del gráfico Q-Q de los residuos
plt.subplot(1, 2, 2)
stats.probplot(residuals_train, dist="norm", plot=plt)
plt.title("Gráfico Q-Q de Residuos (Train)")

# Ajustar el diseño de la figura
plt.tight_layout()
plt.show()