RNN

Las Redes Neuronales Recurrentes (Recurrent Neural Network - RNN) son redes neuronales capaces de manejar datos en secuencias como las series de tiempo de los precios de las acciones.

Una RNN se parece mucho a una red neuronal feedforward, excepto que también tiene conexiones que apuntan hacia atrás.

La RNN más simple está compuesta por una neurona que recibe entradas, produce una salida y envía esa salida a sí misma.

En cada paso de tiempo \(t\) (también llamado frame), esta neurona recurrente recibe las entradas \(x_{(t)}\) así como su propia salida del paso de tiempo anterior y dado que no hay una salida previa en el primer paso de tiempo, generalmente se establece en \(0\). Podemos representar esta pequeña red contra el eje del tiempo, como se muestra en la siguiente figura. Esto se llama desenrollar (unroll) la red a través del tiempo (es la misma neurona recurrente representada una vez por paso de tiempo).

En las neuronas recurrentes, la salida \(\hat{y}\) también es una entrada para el siguiente estado de la neurona. Por tanto, la neurona tendrá las \(X\) como entradas y el estado anterior el cual fue la predicción anterior. Este proceso se repite hasta el último time step.

La siguiente figura muestra el esquema de una neurona recurrente (Neuron Recurrent). Esto es una red neuronal con una sola capa y una sola neurona.

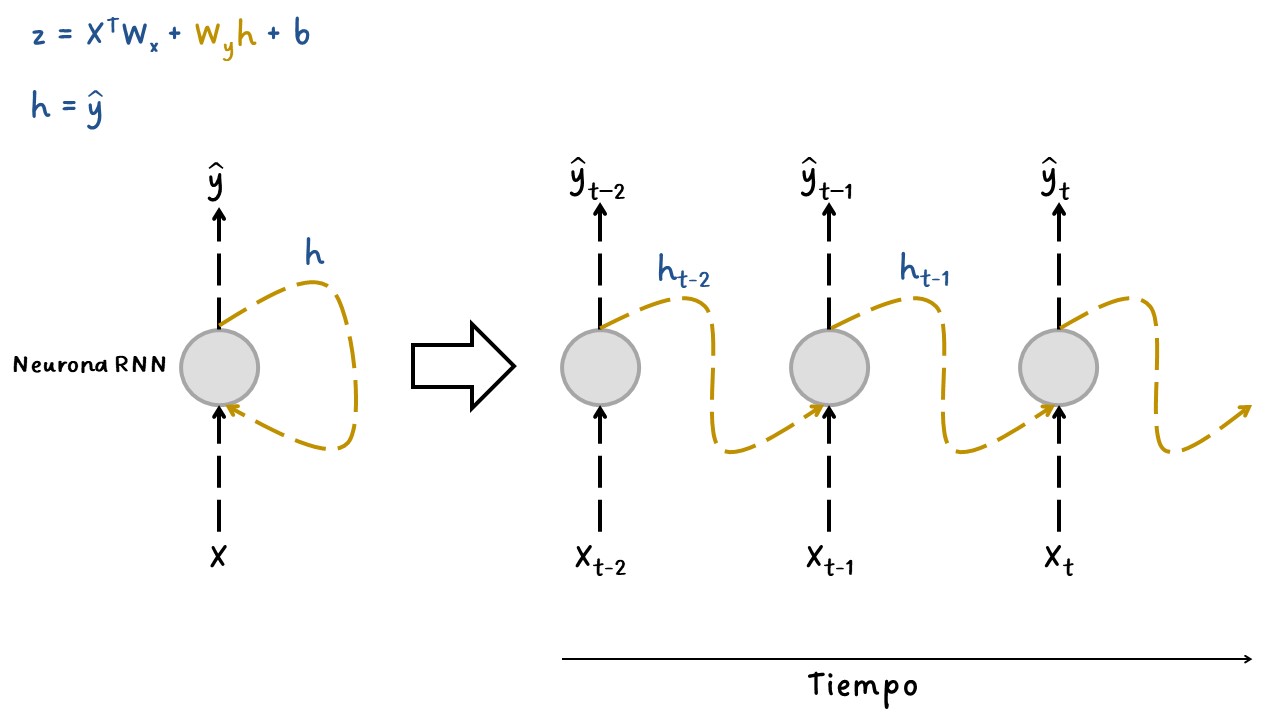
Nueron-Recurrent

Nueron-Recurrent

En cada paso de tiempo \(t\), cada neurona recibe tanto el vector de entrada \(x_{(t)}\) como el vector de salida del paso de tiempo anterior \(y_{(t-1)}\).

Cada neurona recurrente tiene dos conjuntos de pesos: uno para las entradas \(x_{(t)}\) y el otro para las salidas del paso de tiempo anterior, \(y_{(t-1)}\). Llamemos a estos vectores de peso \(w_x\) y \(w_y\). Si consideramos toda la capa recurrente en lugar de solo una neurona recurrente, podemos colocar todos los vectores de peso en dos matrices de peso, \(W_x\) y \(W_y\). El vector de salida de toda la capa recurrente se puede calcular como se muestra en la siguiente ecuación (\(b\) es el vector de bias y \(\phi(\cdot)\) es la función de activación (p. ej., ReLU).

\[y_{(t)}=\phi\left(W_x^Tx_{(t)}+W_y^Ty_{(t-1)}+b\right)\]

Deep RNN:

Lo más común es apilar múltiples capas de neuronas como se muestra en la siguiente figura.

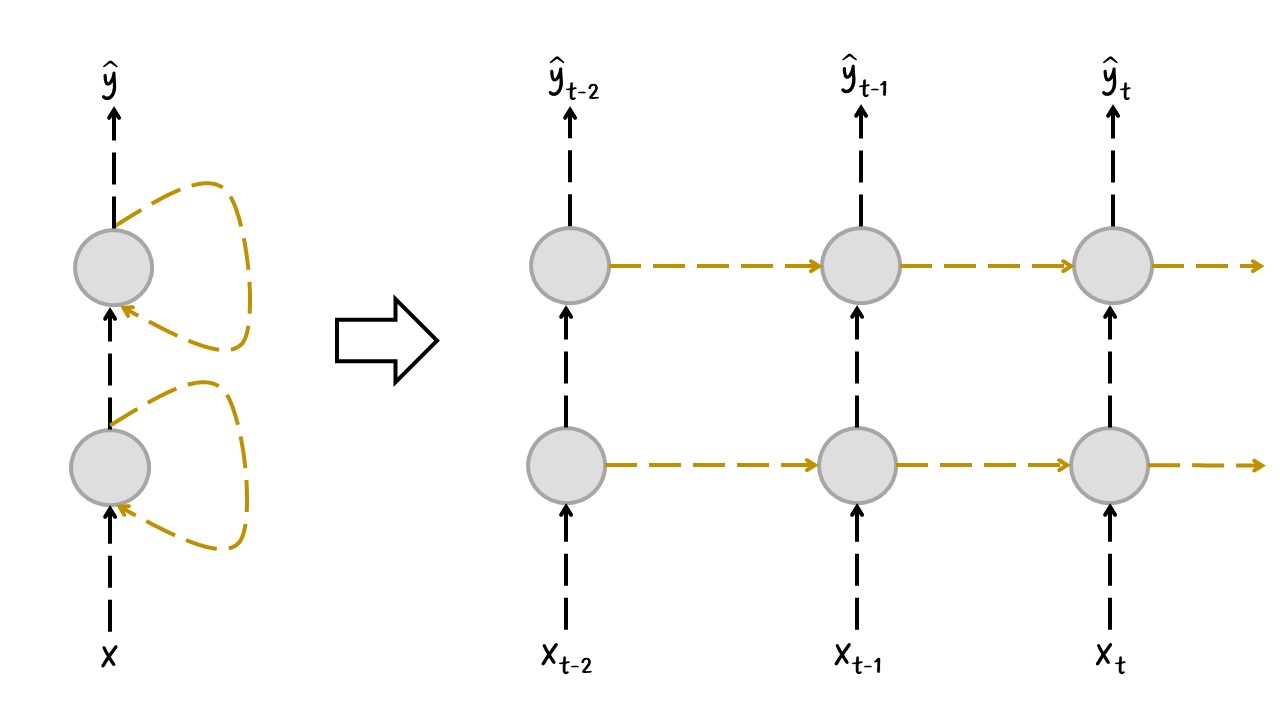
Depp-RNN.jpg

Depp-RNN.jpg

Al igual que con las redes neuronales feedforward, podemos calcular la salida de una capa recurrente de una sola vez para un mini lote completo colocando todas las entradas en el paso de tiempo \(t\) en una matriz de entrada \(X_{(t)}\) como en la siguiente ecuación.

\[Y_{(t)}=\phi\left(X_{(t)}W_x+Y_{(t-1)}W_y+b\right)\]

Donde,

  • \(Y_{(t)}\) es una matriz \(m \times n_{neuronas}\) que contiene las salidas de la capa en el paso de tiempo \(t\) para cada instancia en el mini lote (\(m\) es el número de instancias en el mini lote y \(n_{neuronas}\) es el número de neuronas).

  • \(X_{(t)}\) es una matriz \(m \times n_{inputs}\) que contiene las entradas para todas las instancias (\(n_{inputs}\) es el número de variables de entrada).

  • \(W_x\) es una matriz \(n_{inputs} \times n_{neuronas}\) que contiene los pesos de conexión para las entradas del paso de tiempo actual.

  • \(W_y\) es una matriz \(n_{neuronas} \times n_{neuronas}\) que contiene los pesos de conexión para las salidas del paso de tiempo anterior.

  • \(b\) es un vector de tamaño \(n_{neuronas}\) que contiene el término de bias de cada neurona.

  • Las matrices de ponderación \(W_x\) y \(W_y\) a menudo se concatenan verticalmente en una sola matriz de ponderación \(W\) de forma \((n_{inputs} + n_{neuronas})\times n_{neuronas}\) .

Observe que \(Y_{(t)}\) es una función de \(X_{(t)}\) y \(Y_{(t-1)}\), que es una función de \(X_{(t-1)}\) y \(Y_{(t-2)}\), que es una función de \(X_{(t-2)}\) y \(Y_{(t-3)}\), y así sucesivamente. Esto hace que \(Y_{(t)}\) sea una función de todas las entradas desde el tiempo \(t = 0\) (es decir, \(X_{(0)}\) , \(X_{(1)}\) , …, \(X_{(t)}\)). En el primer paso de tiempo, \(t = 0\), no hay salidas anteriores, por lo que normalmente se supone que son todos ceros.

Celdas de memoria:

Dado que la salida de una neurona recurrente en el paso de tiempo \(t\) es una función de todas las entradas de los pasos de tiempo anteriores, se podría decir que tiene una forma de memoria. Una parte de una red neuronal que conserva algún estado a lo largo de los pasos de tiempo se denomina celda de memoria (Memory Cell) (o simplemente celda). Una sola neurona recurrente, o una capa de neuronas recurrentes, es una celda muy básica, capaz de aprender solo patrones cortos (normalmente de unos 10 pasos de largo, pero esto varía según la tarea).

En general, el estado de una celda en el paso de tiempo \(t\), denotado \(h_{(t)}\) (la “h” significa “oculto” “hidden”), es una función de algunas entradas en ese paso de tiempo y su estado en el paso de tiempo anterior: \(h_{(t)} = f(h_{(t-1)}, x_{(t)})\). Su salida en el paso de tiempo \(t\), denotado \(y_{(t)}\), también es una función del estado anterior y las entradas actuales. En el caso de las celdas básicas que hemos analizado hasta ahora, la salida es simplemente igual al estado, pero en celdas más complejas no siempre es así.

Secuencias de entrada y salida:

Una RNN puede tomar simultáneamente una secuencia de entradas y producir una secuencia de salidas, como se observa en la figura.

Este tipo de red de secuencia a secuencia (sequence-to-sequence network) es útil para predecir series de tiempo como los precios de las acciones: le proporciona los precios de los últimos \(N\) días y debe generar los precios desplazados un día hacia el futuro (es decir, desde \(N – 1\) días hasta mañana).

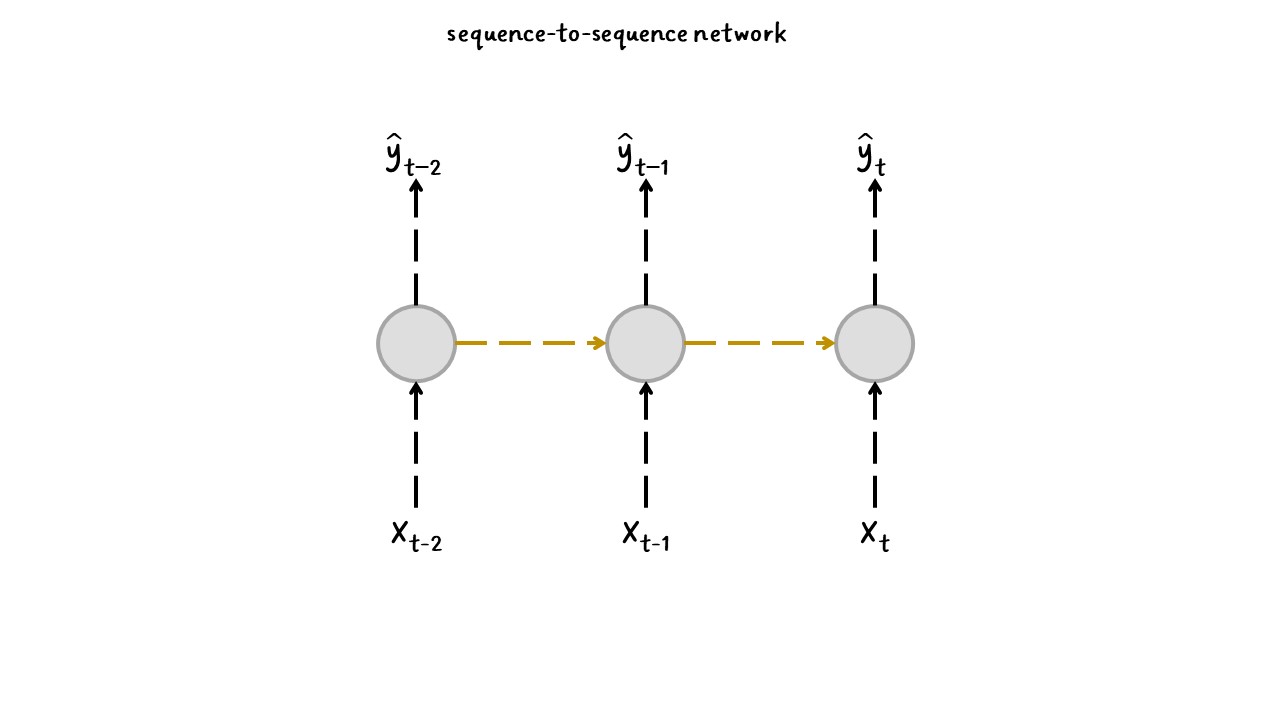
sequence-to-sequence

sequence-to-sequence

Código:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import yfinance as yf
from sklearn.preprocessing import StandardScaler
import warnings  # Para ignorar mensajes de advertencia

warnings.filterwarnings("ignore")

Descargar datos desde Yahoo Finance:

tickers = ["ES=F"]
ohlc = yf.download(tickers, period="max")
print(ohlc.tail())

[*******************100%*********************]  1 of 1 completed
               Open     High      Low    Close  Adj Close   Volume
Date
2022-08-24  4128.25  4158.50  4110.75  4142.75    4142.75  1348612
2022-08-25  4148.75  4202.75  4143.00  4201.00    4201.00  1635476
2022-08-26  4198.25  4217.25  4042.75  4059.50    4059.50  2241117
2022-08-29  4024.00  4064.00  4006.75  4031.25    4031.25  1963446
2022-08-30  4035.75  4072.75  3964.50  3987.50    3987.50  1963446
df = ohlc["Adj Close"].dropna(how="all")
df.tail()

Date
2022-08-24    4142.75
2022-08-25    4201.00
2022-08-26    4059.50
2022-08-29    4031.25
2022-08-30    3987.50
Name: Adj Close, dtype: float64

df = np.array(df[:, np.newaxis])
df.shape

(5548, 1)

plt.figure(figsize=(10, 6))
plt.plot(df)
plt.show()
../../../_images/output_28_02.png

Conjunto de train y test:

time_test = 0.20
train = df[: int(len(df) * (1 - time_test))]
test = df[int(len(df) * (1 - time_test)) :]

plt.plot(train)
plt.xlabel("Tiempo")
plt.ylabel("Precio")
plt.title("Conjunto de train")
plt.show()

plt.plot(test)
plt.xlabel("Tiempo")
plt.ylabel("Precio")
plt.title("Conjunto de test")
plt.show()
../../../_images/output_31_02.png ../../../_images/output_31_11.png

Función para conformar el dataset para datos secuenciales:

def split_sequence(sequence, time_step):
    X, y = list(), list()
    for i in range(len(sequence)):
        end_ix = i + time_step
        if end_ix > len(sequence) - 1:
            break
        seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
        X.append(seq_x)
        y.append(seq_y)
    return np.array(X), np.array(y)

time_step = 5

X_train, y_train = split_sequence(train, time_step)
X_test, y_test = split_sequence(test, time_step)

X_train.shape

(4433, 5, 1)

X_test.shape

(1105, 5, 1)

Arquitectura de la RNN:

Las Redes Neuronales Recurrentes (RNN) en Keras se usan importando SimpleRNN

No se necesita especificar la longitud de las secuencias de entrada ya que una red neuronal recurrente puede procesar cualquier cantidad de pasos en el tiempo (time_step). Por esta razón, en la primera dimensión de entrada se establece None: input_shape=[None, 1]

Si quiere especificar la longitud de las secuencias lo puede hacer así: input_shape=[time_step,1].

Recuerde que las entradas a la red tienen la siguiente forma: [time_step, features]

Al aplicar las capas de neuronas recurrentes en Keras se debe agregar el siguiente argumento return_sequences=True para convertir el modelo en un modelo de secuencia a secuencia y, además, cuando la siguiente capa oculta es también recurrente se debe agregar este argumento para no tener problemas de dimensiones con las matrices.

La función de activación por defecto en Keras es tanh donde las salidas resultan entre -1 y +1, así que, en la capa de salida, lo que se usa es una neurona Dense.

from keras.models import Sequential
from keras.layers import Dense
from keras.layers import SimpleRNN as RNN

model = Sequential()
model.add(RNN(10, activation="selu", return_sequences=True))
model.add(RNN(10, activation="selu", return_sequences=True))
model.add(RNN(4, activation="selu"))
model.add(Dense(1))                           # última capa Dense
model.compile(optimizer="adam", loss="mse")
history = model.fit(
    X_train,
    y_train,
    validation_data=(X_test, y_test),
    epochs=30,
    batch_size=10,
    verbose=0
)

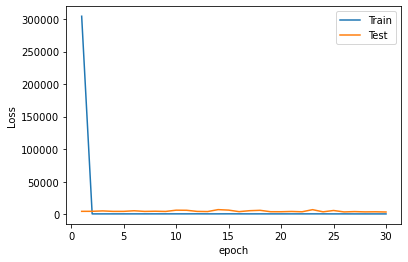
Evaluación del desempeño:

mse = model.evaluate(X_test, y_test, verbose=0)
mse

3454.1025390625

rmse = mse ** 0.5
rmse

58.7716133780799

plt.plot(range(1, len(history.epoch) + 1), history.history["loss"], label="Train")
plt.plot(range(1, len(history.epoch) + 1), history.history["val_loss"], label="Test")
plt.xlabel("epoch")
plt.ylabel("Loss")
plt.legend();
../../../_images/output_47_02.png

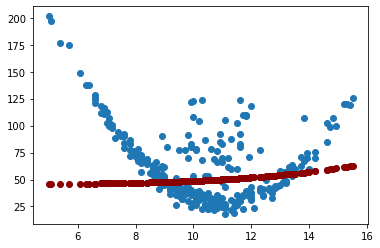
Predicción del modelo:

y_pred = model.predict(X_test, verbose=0)
y_pred[0:5]

array([[2646.0144],
       [2656.9644],
       [2669.1555],
       [2684.126 ],
       [2690.2444]], dtype=float32)

plt.figure(figsize=(18, 6))
plt.plot(
    range(1, len(X_test) + 1),
    test[time_step:, :],
    color="b",
    marker=".",
    linestyle="-",
    label="True"
)
plt.plot(
    range(1, len(X_test) + 1),
    y_pred,
    color="g",
    marker=".",
    linestyle="-",
    label="y_pred"
)
plt.legend();
../../../_images/output_50_01.png

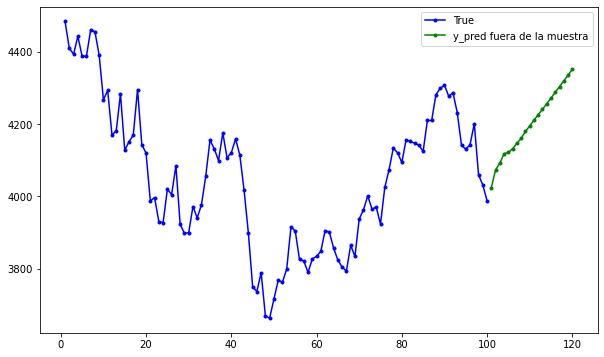
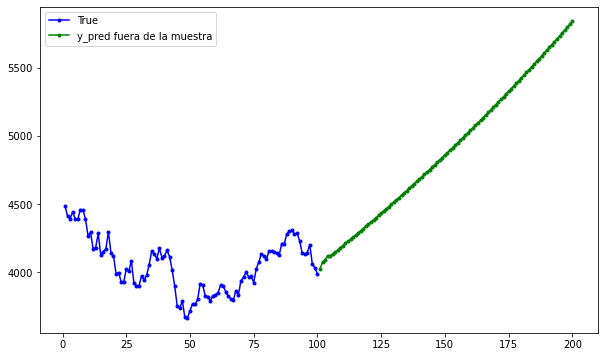
Predicción fuera de la muestra:

Predicción fuera de la muestra para 20 períodos:

predictions = []

time_prediction = 20  # cantidad de predicciones fuera de la muestra

first_sample = df[-time_step:, 0]                             # última muestra dentro de la serie de tiempo
current_batch = first_sample[np.newaxis]                      # Transformación en muestras y time step
current_batch = np.reshape(current_batch, (1, time_step, 1))  # Transformación en 3D

for i in range(time_prediction):

    current_pred = model.predict(current_batch, verbose=0)[0]

    # Guardar la predicción
    predictions.append(current_pred)

    # Actualizar el lote para incluir ahora la predicción y soltar el primer valor (primer time step)
    current_batch = np.append(current_batch[:, 1:], [[current_pred]])[np.newaxis]
    current_batch = np.reshape(current_batch, (1, time_step, 1))  # Transformación en 3D

plt.figure(figsize=(10, 6))
plt.plot(
    range(1, len(df[-100:, 0]) + 1),
    df[-100:, 0],
    color="b",
    marker=".",
    linestyle="-",
    label="True"
)
plt.plot(
    range(len(df[-100:, 0]) + 1, len(df[-100:, 0]) + len(predictions) + 1),
    predictions,
    color="g",
    marker=".",
    linestyle="-",
    label="y_pred fuera de la muestra"
)
plt.legend();
../../../_images/output_54_01.png