Ejemplo reducción de dimensionalidad

Generación de datos en espiral en 3D:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA, KernelPCA

# Generación de la espiral en 3D
def generate_spiral(n_points=1000, noise=0.1):
    theta = np.linspace(0, 4 * np.pi, n_points)
    z = np.linspace(-2, 2, n_points)
    r = z ** 2 + 1
    x = r * np.sin(theta)
    y = r * np.cos(theta)

    # Añadir ruido
    x += noise * np.random.randn(n_points)
    y += noise * np.random.randn(n_points)
    z += noise * np.random.randn(n_points)

    return np.vstack((x, y, z)).T


X = generate_spiral()

# Visualización de la espiral en 3D
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection="3d")
ax.scatter(X[:, 0], X[:, 1], X[:, 2])
ax.set_xlabel("X-axis")
ax.set_ylabel("Y-axis")
ax.set_zlabel("Z-axis")
plt.title("3D Spiral")
plt.show()

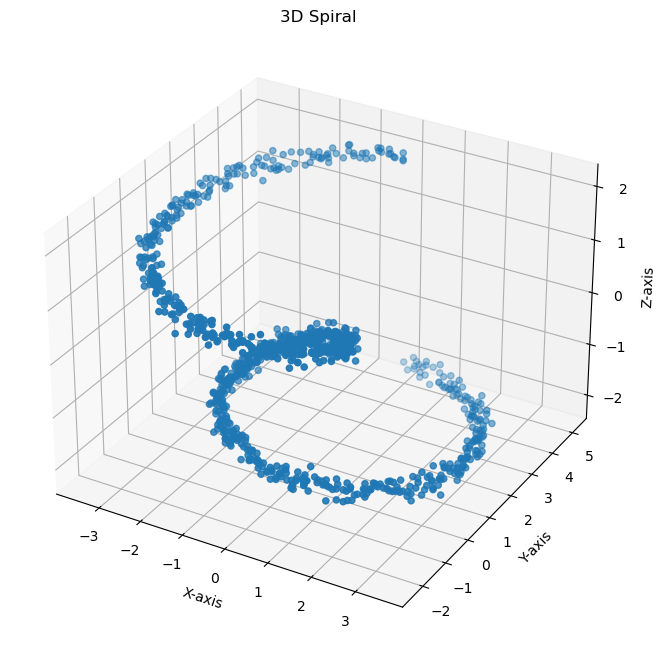
Estandarización de los datos:

Para asegurar un proceso completo y preciso, debemos estandarizar los datos antes de aplicar PCA. Esto es crucial para que PCA funcione correctamente.

# Estandarización de los datos
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

PCA:

# Aplicación de PCA estándar
pca = PCA()
pca.fit(X_scaled)

# Cálculo de las varianzas explicadas
explained_variance = pca.explained_variance_ratio_

print("Varianza explicada por cada componente principal:")
print(explained_variance)

# Cálculo de la varianza explicada acumulada
explained_variance_cum = np.cumsum(pca.explained_variance_ratio_)

# Matriz de componentes principales (matriz de rotación)
rotation_matrix = pca.components_.T

print("Matriz de Rotación:\n", rotation_matrix)

# Visualización del gráfico de varianza explicada
plt.figure(figsize=(8, 6))
plt.plot(
    range(1, len(explained_variance_cum) + 1),
    explained_variance_cum,
    marker="o",
    linestyle="--",
)
plt.xlabel("Número de Componentes Principales")
plt.ylabel("Varianza Explicada Acumulada")
plt.title("Gráfico de Varianza Explicada Acumulada")
plt.grid()
plt.show()

Varianza explicada por cada componente principal:
[0.55901416 0.33333707 0.10764878]
Matriz de Rotación:
 [[ 0.70709439 -0.00658215 -0.70708854]
 [ 0.00376586  0.99997755 -0.00554271]
 [-0.70710915 -0.00125643 -0.7071033 ]]

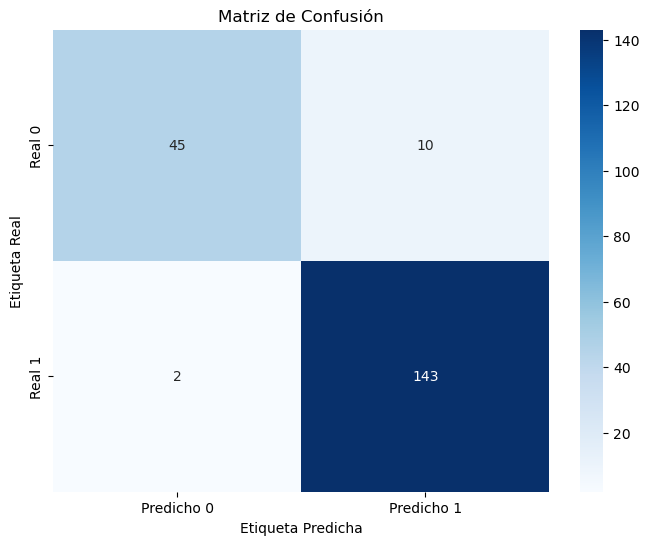
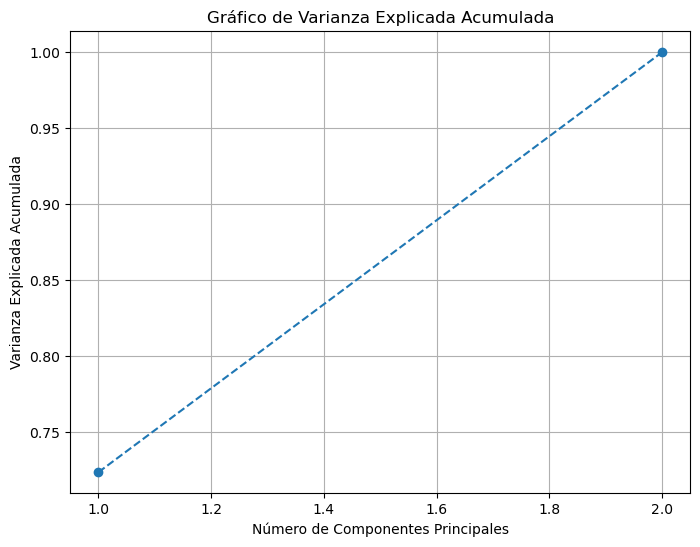
Con dos Componentes Principales se explica aproximadamente el 90% de la varianza de los datos.

n_components=2

# Aplicación de PCA estándar
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

# Visualización de PCA estándar
plt.figure(figsize=(8, 6))
plt.scatter(X_pca[:, 0], X_pca[:, 1])
plt.xlabel("Principal Component 1")
plt.ylabel("Principal Component 2")
plt.title("PCA Standard")
plt.show()

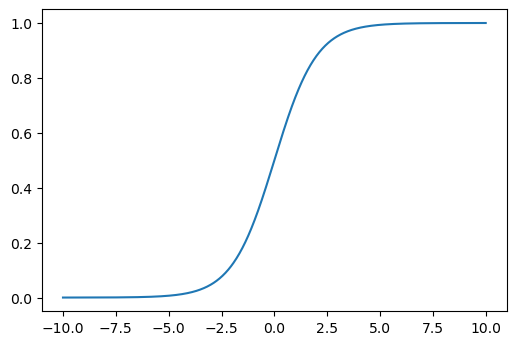
Kernel PCA:

Por defecto Scikit-learn en KernelPCA usa kernel='linear', aunque tiene los siguientes Kernels:

'poly', 'rbf', 'sigmoid', 'cosine'

# Aplicación de Kernel PCA con kernel RBF
kpca = KernelPCA(n_components=2, kernel="rbf", gamma=15)
X_kpca = kpca.fit_transform(X_scaled)

# Visualización de Kernel PCA
plt.figure(figsize=(8, 6))
plt.scatter(X_kpca[:, 0], X_kpca[:, 1])
plt.xlabel("Principal Component 1")
plt.ylabel("Principal Component 2")
plt.title("Kernel PCA (RBF Kernel)")
plt.show()

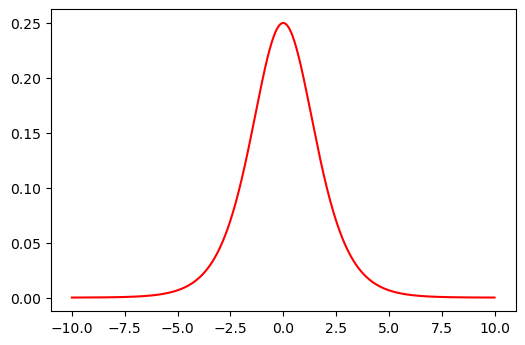
¿Cómo cambia el resultado para valores diferentes de gamma=?

Generación de datos en forma de media luna:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.decomposition import PCA, KernelPCA
from sklearn.preprocessing import StandardScaler

# Generación de datos en forma de media luna
X, y = make_moons(n_samples=1000, noise=0.1)

# Visualización de los datos originales
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="viridis")
plt.xlabel("X-axis")
plt.ylabel("Y-axis")
plt.title("Datos en forma de media luna")
plt.show()

# Estandarización de los datos
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

PCA:

# Aplicación de PCA estándar
pca = PCA()
pca.fit(X_scaled)

# Cálculo de las varianzas explicadas
explained_variance = pca.explained_variance_ratio_

print("Varianza explicada por cada componente principal:")
print(explained_variance)

# Cálculo de la varianza explicada acumulada
explained_variance_cum = np.cumsum(pca.explained_variance_ratio_)

# Matriz de componentes principales (matriz de rotación)
rotation_matrix = pca.components_.T

print("Matriz de Rotación:\n", rotation_matrix)

# Visualización del gráfico de varianza explicada
plt.figure(figsize=(8, 6))
plt.plot(
    range(1, len(explained_variance_cum) + 1),
    explained_variance_cum,
    marker="o",
    linestyle="--",
)
plt.xlabel("Número de Componentes Principales")
plt.ylabel("Varianza Explicada Acumulada")
plt.title("Gráfico de Varianza Explicada Acumulada")
plt.grid()
plt.show()

Varianza explicada por cada componente principal:
[0.72348618 0.27651382]
Matriz de Rotación:
 [[-0.70710678 -0.70710678]
 [ 0.70710678 -0.70710678]]

# Aplicación de PCA estándar
pca = PCA(n_components=1)
X_pca = pca.fit_transform(X_scaled)

# Agregar un eje Y artificial para la visualización
X_pca_1d_plot = np.hstack((X_pca, np.zeros((X_pca.shape[0], 1))))

# Visualización de PCA con un solo componente principal
plt.figure(figsize=(8, 6))
plt.scatter(X_pca_1d_plot[:, 0], X_pca_1d_plot[:, 1], c=y, cmap="viridis")
plt.xlabel("Componente Principal 1")
plt.ylabel("Valor Fijo (0)")
plt.title("PCA con un solo Componente Principal")
plt.show()

Kernel PCA:

# Aplicación de Kernel PCA con kernel RBF
kpca = KernelPCA(n_components=1, kernel="rbf", gamma=15)
X_kpca = kpca.fit_transform(X_scaled)

# Agregar un eje Y artificial para la visualización
X_pca_1d_plot = np.hstack((X_kpca, np.zeros((X_kpca.shape[0], 1))))

# Visualización de PCA con un solo componente principal
plt.figure(figsize=(8, 6))
plt.scatter(X_pca_1d_plot[:, 0], X_pca_1d_plot[:, 1], c=y, cmap="viridis")
plt.xlabel("Componente Principal 1")
plt.ylabel("Valor Fijo (0)")
plt.title("PCA con un solo Componente Principal")
plt.show()