Estadística aplicada a los activos bursátiles

Utilizar el archivo Cuatro acciones 2020.csv.

Importar datos.

datos = read.csv("Cuatro acciones 2020.csv", sep = ";", dec = ",", header = T)

head(datos)
A data.frame: 6 × 5
FechaECOPFAVALISANUTRESA
<fct><int><int><int><int>
126/03/2018277511651308025720
227/03/2018264511551308025700
328/03/2018261511651332025980
42/04/2018 269011651342025920
53/04/2018 273011751366025920
64/04/2018 274011901356025840

Matriz de precios.

precios = datos[,-1]

head(precios)
A data.frame: 6 × 4
ECOPFAVALISANUTRESA
<int><int><int><int>
1277511651308025720
2264511551308025700
3261511651332025980
4269011651342025920
5273011751366025920
6274011901356025840

Nombres de las acciones.

colnames extrae los nombres de los encabezados.

nombres = colnames(precios)
nombres
  1. 'ECO'
  2. 'PFAVAL'
  3. 'ISA'
  4. 'NUTRESA'

ncol cuanta cuántas columnas tiene las matrices.

acciones = ncol(precios)
acciones
4

Conversión de la base de datos como serie de tiempo.

La función ts hace una conversión a los precios como series de tiempo. Este paso puede ser opcional.

precios = ts(precios)

Gráfica de los precios de las acciones.

plot(precios, t = "l", xlab = "Tiempo")
../../_images/output_17_03.png

Rendimientos de las acciones.

Rendimiento discreto:

\[Rendimiento_t=\frac{Precio_t-Precio_{t-1}}{Precio_{t-1}}=\frac{Precio_t}{Precio_{t-1}}-1\]

Conversión de tasas discretas a continuas:

\[log(1+r)\]

Rendimiento continuo o logarítmico o geométrico:

\[Rendimiento_t=log(1+Rendimiento_{discreto})\]
\[Rendimiento_t=log\frac{Precio_t}{Precio_{t-1}}\]

Los rendimientos discretos y continuos se aproximan cuando el rendimiento es pequeño, y los rendimientos serán pequeños si se trara de un horizonte de tiempo corto.

En adelante, usaremos los rendimientos continuos.

De las propiedades de los logaritmos tenemos:

\[log\frac{Precio_t}{Precio_{t-1}}=log(Precio_t)-log(Precio_{t-1})\]

Matriz de rendimientos.

Con log(precios[,i] se aplica la función de logaritmo natural a todos los precios y con la función diff se calcula la diferencia de los logaritmos que de las propiedades de los logaritmo mencionada anteriormente, se llega a los rendimientos por período de cada acción

rendimientos <- matrix(0, nrow(precios) -1, acciones)

for(i in 1:acciones){

  rendimientos[,i] = diff(log(precios[,i]))

}

Cuando se aplica la función ts a los precios, no es necesario utilizar el código anterior para calcular los rendimientos. Se puede hacer de la siguiente manera:

rendimientos = diff(log(precios))

head(rendimientos)
A matrix: 6 × 4 of type dbl
ECOPFAVALISANUTRESA
-0.047979682-0.008620743 0.000000000-0.0007779075
-0.011406968 0.008620743 0.018182319 0.0108360193
0.028277096 0.000000000 0.007479466-0.0023121398
0.014760416 0.008547061 0.017725723 0.0000000000
0.003656311 0.012685160-0.007347572-0.0030911926
0.000000000 0.020790770 0.023324673 0.0153612852

Si se tiene \(n\) cantidad de precios, se tendrá \(n-1\) rendimientos. Cada acción acción tiene 500 precios, entonces, se tendrán 499 rendimientos.

El tamaño de un vector o columna se calcula con dim.

dim(precios)
  1. 500
  2. 4
dim(rendimientos)
  1. 499
  2. 4

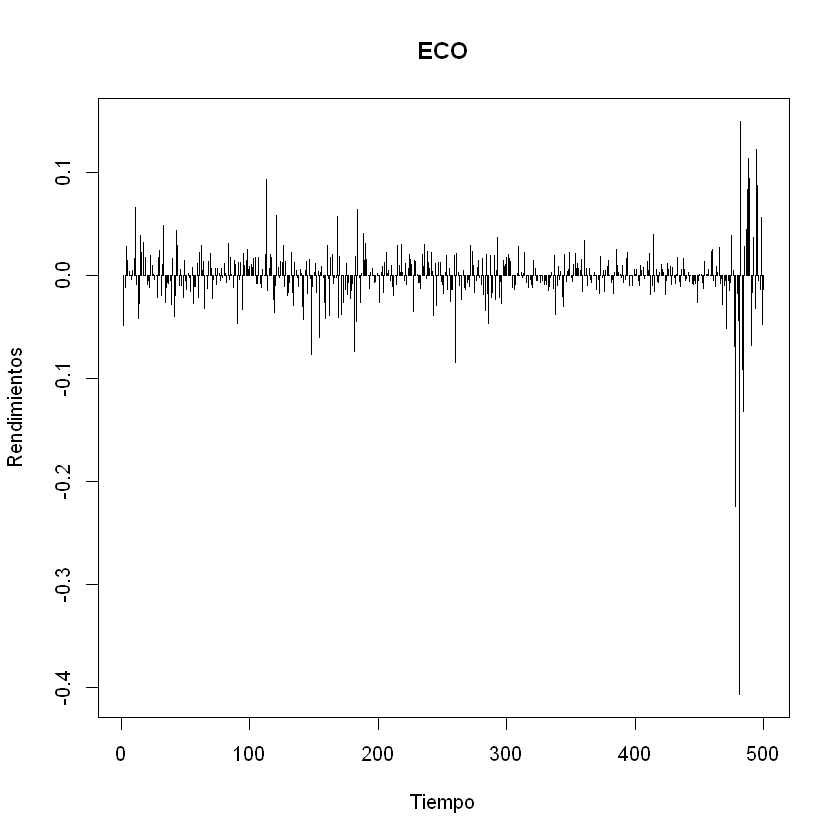
Gráficas de los rendimientos de las acciones.

plot(rendimientos[,1], t = "h", xlab = "Tiempo", ylab = "Rendimientos", main = nombres[1])
../../_images/output_30_04.png 
plot(rendimientos[,2], t = "h", xlab = "Tiempo", ylab = "Rendimientos", main = nombres[2])
../../_images/output_31_03.png 
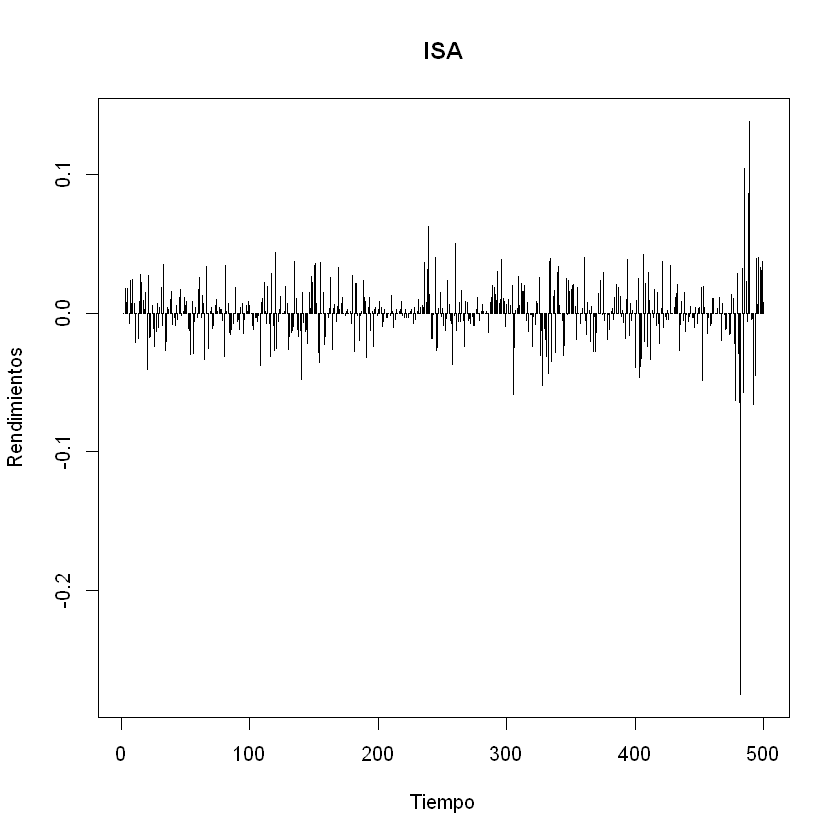
plot(rendimientos[,3], t = "h", xlab = "Tiempo", ylab = "Rendimientos", main = nombres[3])
../../_images/output_32_05.png 
plot(rendimientos[,4], t = "h", xlab = "Tiempo", ylab = "Rendimientos", main = nombres[4])
../../_images/output_33_02.png

Los cuatro gráficos anteriores se pueden juntar en uno solo. En R se utiliza el siguiente código para dividir la ventana donde salen los gráficos. Primero se crea una matriz con las posiciones que queremos tener y después se muestra la matriz con layout.show().

layout(matrix(c(1:4),nrow=2,byrow=F))
layout.show(4)
../../_images/output_35_02.png

Para quitar la partición a la ventana plot se debe correo el código dev.off(). Así los gráficos saldran del tamaño de la ventana y un solo un gráfico por ventana.

layout(matrix(c(1:4), nrow = 2, byro w= F))
layout.show(4)
for(i in 1:acciones){

    plot(rendimientos[,i], t = "h", xlab = "Tiempo", ylab = "Rendimientos", main = nombres[i])
}
../../_images/output_37_03.png

Estadísticas básicas de los rendimientos

summary(rendimientos)

     ECO                 PFAVAL                ISA
Min.   :-0.4065868   Min.   :-0.4038136   Min.   :-0.2756262
1st Qu.:-0.0096775   1st Qu.:-0.0077671   1st Qu.:-0.0084762
Median : 0.0000000   Median : 0.0000000   Median : 0.0012682
Mean   :-0.0004472   Mean   :-0.0003983   Mean   : 0.0006398
3rd Qu.: 0.0117059   3rd Qu.: 0.0081301   3rd Qu.: 0.0101129
Max.   : 0.1498123   Max.   : 0.2058521   Max.   : 0.1386834
   NUTRESA
Min.   :-0.105361
1st Qu.:-0.006312
Median : 0.000000
Mean   :-0.000268
3rd Qu.: 0.005472
Max.   : 0.065983

Se debe instalar el paquete install.packages("fBasics"). Utilizar el código anterior en R para instalar el paquete. Después de instalar, se llama la librería fBasics.

library(fBasics)

basicStats(rendimientos)
A data.frame: 16 × 4
ECOPFAVALISANUTRESA
<dbl><dbl><dbl><dbl>
nobs499.000000499.000000499.000000499.000000
NAs 0.000000 0.000000 0.000000 0.000000
Minimum -0.406587 -0.403814 -0.275626 -0.105361
Maximum 0.149812 0.205852 0.138683 0.065983
1. Quartile -0.009678 -0.007767 -0.008476 -0.006312
3. Quartile 0.011706 0.008130 0.010113 0.005472
Mean -0.000447 -0.000398 0.000640 -0.000268
Median 0.000000 0.000000 0.001268 0.000000
Sum -0.223144 -0.198765 0.319287 -0.133754
SE Mean 0.001429 0.001278 0.001062 0.000627
LCL Mean -0.003256 -0.002910 -0.001447 -0.001500
UCL Mean 0.002361 0.002113 0.002727 0.000964
Variance 0.001020 0.000816 0.000563 0.000196
Stdev 0.031932 0.028558 0.023729 0.014010
Skewness -4.487458 -4.641477 -2.657806 -0.908069
Kurtosis 57.943763 87.840091 38.693818 11.122682

Rendimientos esperados.

El rendimiento esperado es el promedio de los 499 rendimientos de cada acción. La función mean calcula el promedio.

El rendimiento esperado de cada acción se puede calcular de dos formas:

Forma 1:

rendimientos_esperados = vector()

for(i in 1:acciones){

    rendimientos_esperados[i] = mean(rendimientos[,i])

}
rendimientos_esperados
  1. -0.000447181465559539
  2. -0.000398326704447035
  3. 0.000639854532799824
  4. -0.000268043266851791

Forma 2:

Se puede utilizar la función apply. En esta función se debe indicar el valor de 1para aplicar otra función a las filas del vector o matriz o el valor 2 para aplicar otra función a las columnas. En este caso se aplicará mean a las columnas de las matriz de rendimientos.

rendimientos_esperados = apply(rendimientos, 2, mean)
rendimientos_esperados
ECO
-0.000447181465559539
PFAVAL
-0.000398326704447035
ISA
0.000639854532799824
NUTRESA
-0.000268043266851791

La frecuencia de las series de tiempo cargadas es diaria, esto implica que los resultados tendrán la misma frecuencia temporal. Por tanto, los rendimientos son diarios.

Rendimiento esperado:

ECO: -0,000447 \(=\) -0,0447% diario.

PFVAVAL: -0,000398 \(=\) -0,0398% diario.

ISA: -0,000640 \(=\) -0,0640% diario.

NUTRESA: -0,000268 \(=\) -0,0268% diario.

Volatilidad o desviación estándar

La volatilidad de las acciones se calculan con la funciónsd.

La volatilidad de cada acción se puede calcular de dos formas:

Forma 1:

volatilidades = vector()

for(i in 1:acciones){

    volatilidades[i ]= sd(rendimientos[,i])

}
volatilidades
  1. 0.0319324424190137
  2. 0.0285577211893029
  3. 0.0237292026947701
  4. 0.0140104740592151

Forma 2:

volatilidades = apply(rendimientos, 2, sd)
volatilidades
ECO
0.0319324424190137
PFAVAL
0.0285577211893029
ISA
0.0237292026947701
NUTRESA
0.0140104740592151

Volatilidad:

ECO: 0,0319 \(=\) 3,19% diario.

PFVAVAL: 0,0286 \(=\) 2,86% diario.

ISA: 0,0237 \(=\) 2,37% diario.

NUTRESA: 0,0140 \(=\) 1,40% diario.

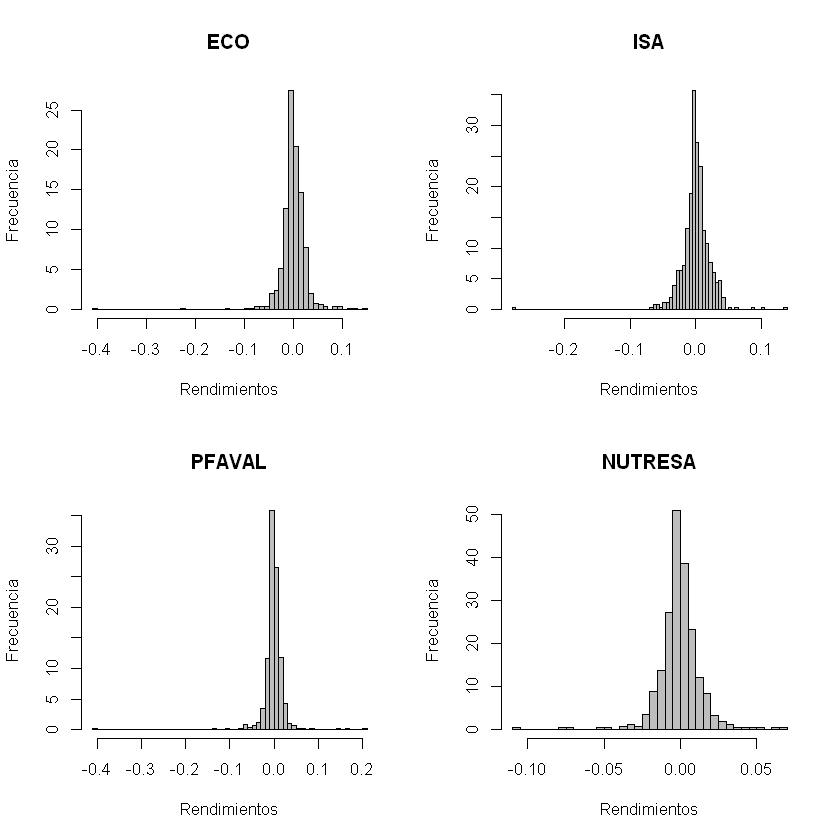
Histograma de los rendimientos.

layout(matrix(c(1:4), nrow = 2, byrow = F))

for(i in 1:acciones){

    hist(rendimientos[,i], breaks = 60, col = "gray", xlab = "Rendimientos", ylab = "Frecuencia", main = nombres[i], freq = F)
}
../../_images/output_59_01.png

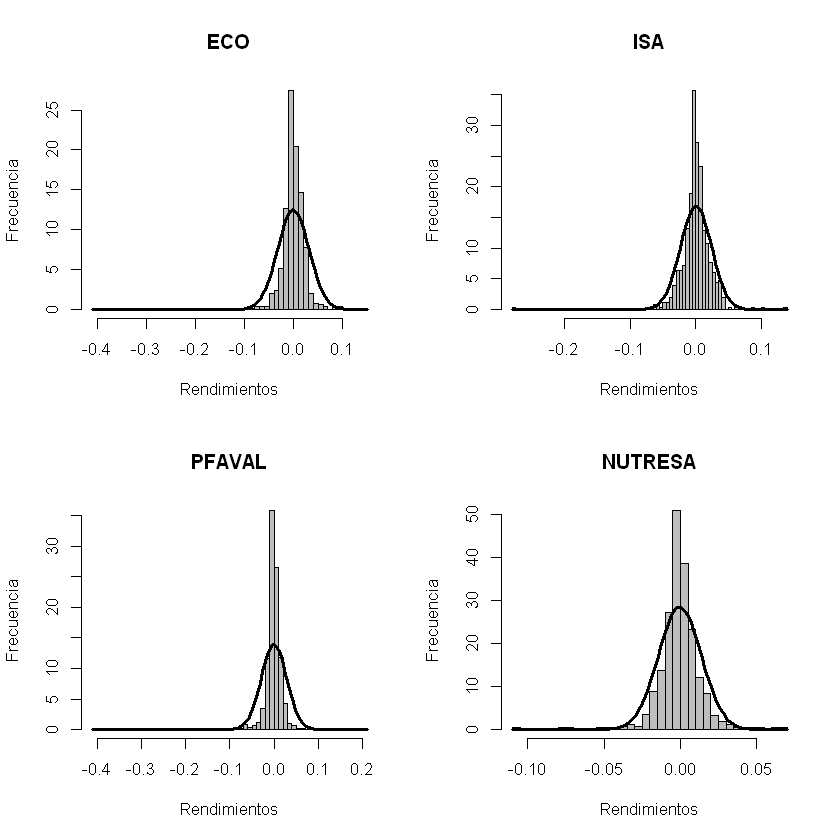
Histograma y distribución normal.

layout(matrix(c(1:4), nrow = 2, byrow = F))

for(i in 1:acciones){

    hist(rendimientos[,i], breaks = 60, col = "gray", xlab = "Rendimientos", ylab = "Frecuencia", main = nombres[i], freq = F)
    curve(dnorm(x, mean = rendimientos_esperados[i], sd = volatilidades[i]), add = T, lwd = 3)
}
../../_images/output_61_01.png

Histograma y densidad.

layout(matrix(c(1:4), nrow = 2, byrow = F))

for(i in 1:acciones){

    hist(rendimientos[,i], breaks = 60, col = "gray", xlab = "Rendimientos", ylab = "Frecuencia", main = nombres[i], freq = F)
    lines(density(rendimientos[,i]), lwd = 3, col = "darkgreen")
}
../../_images/output_63_03.png

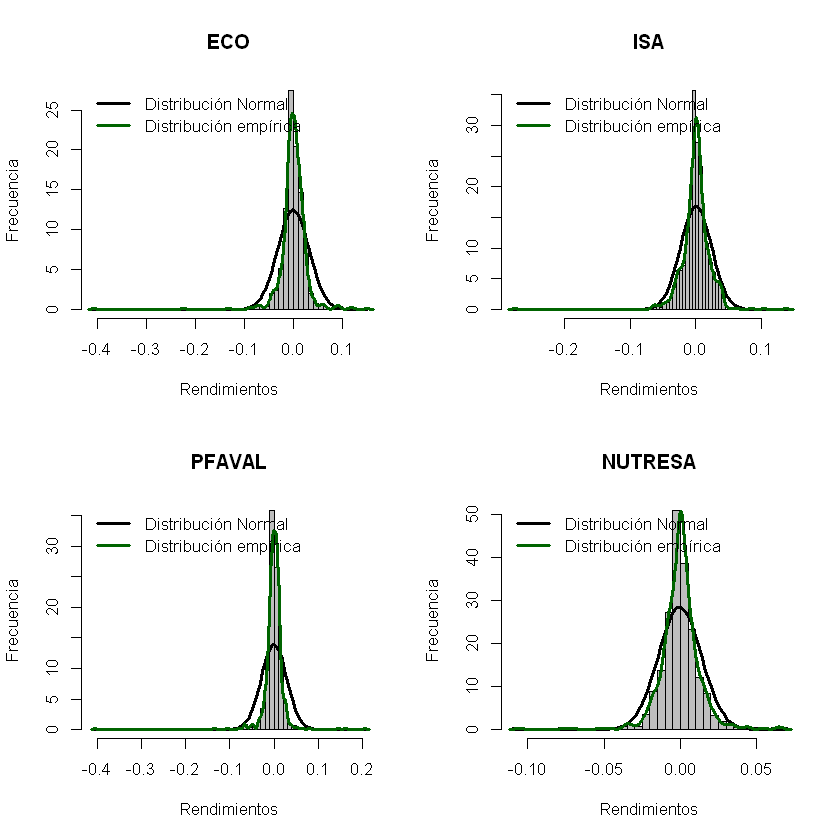
Histograma, distribución normal y densidad.

layout(matrix(c(1:4), nrow = 2, byrow = F))

for(i in 1:acciones){

    hist(rendimientos[,i], breaks = 60, col = "gray", xlab = "Rendimientos", ylab = "Frecuencia", main = nombres[i], freq = F)
    curve(dnorm(x, mean = rendimientos_esperados[i], sd = volatilidades[i]), add = T, lwd = 3)
    lines(density(rendimientos[,i]), lwd = 3, col = "darkgreen")
    legend("topleft", c("Distribución Normal", "Distribución empírica"), lty = c(1,1), lwd = c(3,3), col = c("black", "darkgreen"), bty = "n")
}
../../_images/output_65_0.png

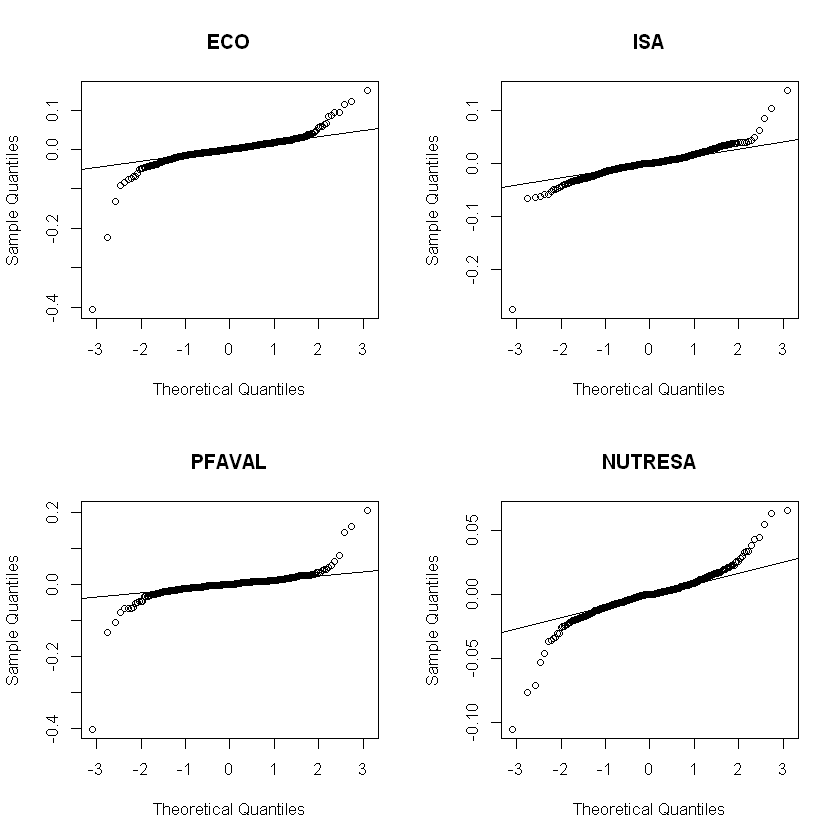
Análisis de normalidad.

Se hace una comparación de cada cuatíl de la distribución empírica con respecto a la distribución normal. La línea recta es una guía.

Estas gráficas se llaman Q-Q plot.

layout(matrix(c(1:4), nrow = 2, byrow = F))

for(i in 1:acciones){

    qqnorm(rendimientos[,i], main = nombres[i])
    qqline(rendimientos[,i])
}
../../_images/output_68_01.png

Covarianza

Es una medida de relación lineal entre dos variables aleatorios describiendo el movimiento conjunto entre éstas.

covarianza = cov(rendimientos)
covarianza
A matrix: 4 × 4 of type dbl
ECOPFAVALISANUTRESA
ECO0.00101968090.00059394680.00011603270.0001493216
PFAVAL0.00059394680.00081554340.00015643600.0001322689
ISA0.00011603270.00015643600.00056307510.0001519996
NUTRESA0.00014932160.00013226890.00015199960.0001962934

Correlación

Mide el grado de movimiento conjunto entre dos variables o la relación lineal entre ambas en un rango entre -1 y +1.

correlacion = cor(rendimientos)
correlacion
A matrix: 4 × 4 of type dbl
ECOPFAVALISANUTRESA
ECO1.00000000.65131610.15313170.3337626
PFAVAL0.65131611.00000000.23085010.3305836
ISA0.15313170.23085011.00000000.4572004
NUTRESA0.33376260.33058360.45720041.0000000