XGBoost para series de tiempo

import numpy as np
import pandas as pd
import xgboost as xgb
from sklearn.model_selection import train_test_split, RandomizedSearchCV
from sklearn.metrics import r2_score
import matplotlib.pyplot as plt
import scipy.stats as stats

import warnings

# Suprimir todas las advertencias
warnings.filterwarnings("ignore")

# Cargar los datos omitiendo la primera fila como encabezado y asignando nombres a las columnas
data = pd.read_csv("../Irradiance_mensual.csv", skiprows=1, header=None, names=['Fecha', 'Irradiancia'])

# Convertir la columna 'Fecha' a datetime
data['Fecha'] = pd.to_datetime(data['Fecha'], format='%Y-%m')

# Set 'Fecha' as the index
data.set_index('Fecha', inplace=True)

# Cantidad de datos
n = data.shape[0]
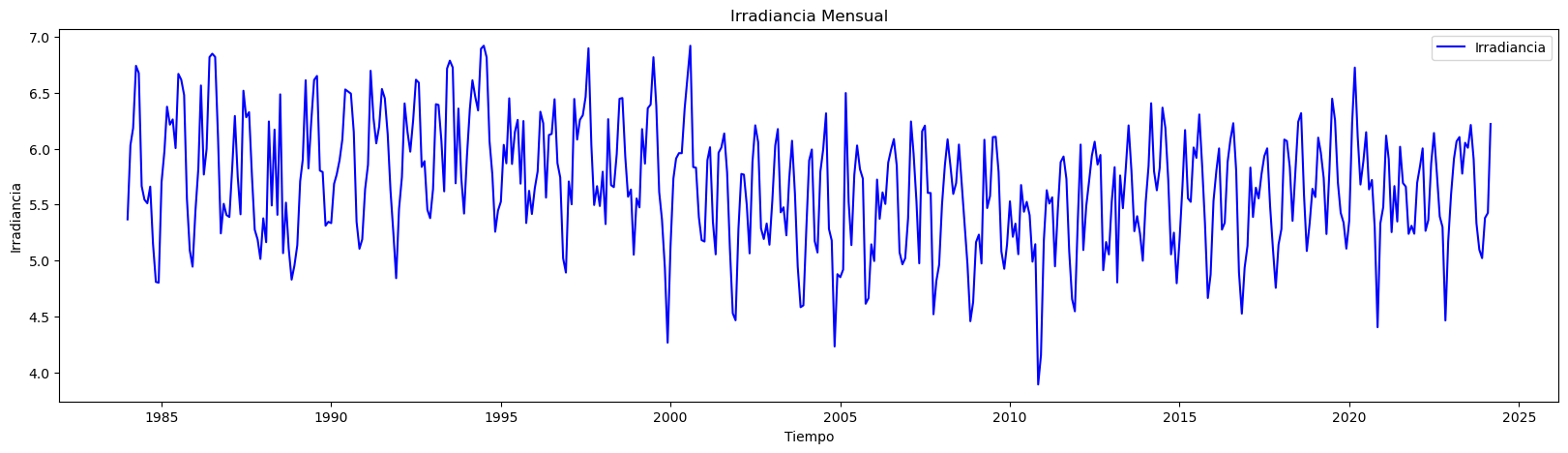
print("Cantidad de datos:", n)

plt.figure(figsize=(20, 5))  # Establecer el tamaño del gráfico
plt.plot(data.index, data['Irradiancia'], label='Irradiancia', color='blue')  # Dibujar los datos reales
plt.title('Irradiancia Mensual')  # Título del gráfico
plt.xlabel('Tiempo')  # Etiqueta del eje X
plt.ylabel('Irradiancia')  # Etiqueta del eje Y
plt.legend()  # Añadir leyenda para identificar las líneas
plt.show()

Cantidad de datos: 483

Conjunto de Train y Test

# Definir características (X) y objetivo (y)
X = data[["Irradiancia"]]  # Usar la irradiancia como característica
y = data["Irradiancia"]  # Usar la irradiancia también como objetivo

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=False)

XGBoost para regresión:

Optimización de hiperparámetros:

# Crear el modelo de XGBoost para regresión
xgboost_regressor = xgb.XGBRegressor(objective="reg:squarederror", random_state=34)

# Definir el espacio de hiperparámetros
param_dist = {
    "n_estimators": np.arange(100, 1000, 100),
    # Número de árboles en el modelo (también conocido como número de iteraciones de boosting).
    "max_depth": np.arange(3, 10, 1),
    # Profundidad máxima de cada árbol. Aumentar este valor hace que el modelo sea más complejo y más propenso al sobreajuste.
    "learning_rate": np.linspace(0.01, 0.3, 10),
    # Tasa de aprendizaje, que reduce la contribución de cada árbol individual para evitar el sobreajuste.
    "subsample": np.linspace(0.5, 1.0, 10),
    # Fracción de muestras utilizadas para entrenar cada árbol. Útil para reducir la varianza del modelo.
    "colsample_bytree": np.linspace(0.5, 1.0, 10),
    # Fracción de características seleccionadas al azar para entrenar cada árbol. Ayuda a reducir la correlación entre árboles.
    "gamma": np.linspace(0, 0.5, 5),
    # Mínima reducción de la pérdida necesaria para hacer una división adicional en un nodo del árbol. Mayor gamma significa árboles más conservadores.
    "reg_alpha": np.linspace(0, 1, 10),
    # Término de regularización L1 (Lasso). Controla la complejidad del modelo penalizando los pesos grandes.
    "reg_lambda": np.linspace(0, 1, 10)
    # Término de regularización L2 (Ridge). También controla la complejidad del modelo, pero penaliza los pesos en función de su magnitud cuadrática.
}


# Configurar RandomizedSearchCV
random_search = RandomizedSearchCV(
    estimator=xgboost_regressor,
    param_distributions=param_dist,
    n_iter=100,  # Número de combinaciones aleatorias a evaluar
    scoring="neg_mean_squared_error",
    cv=5,
    verbose=2,
    random_state=34,
    n_jobs=-1,  # Usar todos los núcleos disponibles
)

# Ajustar RandomizedSearchCV al conjunto de entrenamiento
random_search.fit(X_train, y_train)

# Obtener el mejor modelo
best_xgb_model = random_search.best_estimator_

print("Mejores hiperparámetros encontrados: ", random_search.best_params_)

Fitting 5 folds for each of 100 candidates, totalling 500 fits
Mejores hiperparámetros encontrados:  {'subsample': 0.9444444444444444, 'reg_lambda': 0.7777777777777777, 'reg_alpha': 0.0, 'n_estimators': 300, 'max_depth': 4, 'learning_rate': 0.3, 'gamma': 0.0, 'colsample_bytree': 0.6111111111111112}

# Entrenar el modelo de XGBoost con los datos de entrenamiento
best_xgb_model = xgboost_regressor.fit(X_train, y_train)

Evaluación del modelo:

# Predecir los datos de entrenamiento
y_pred_train = best_xgb_model.predict(X_train)

# Predecir los datos de prueba
y_pred = best_xgb_model.predict(X_test)

## Calcular R² Score Train:
r2_train = r2_score(y_train, y_pred_train)
print("R² Score Train:", r2_train)

# Calcular R² Score Test:
r2_test = r2_score(y_test, y_pred)
print("R² Score Test:", r2_test)

R² Score Train: 0.9996391767157554
R² Score Test: 0.9980910892186873

# Gráfica de resultados
plt.figure(figsize=(14, 7))
plt.plot(y_test.index, y_test.values, label="Test", color="green")
plt.plot(y_test.index, y_pred, label="Predicted", linestyle="--", color="red")
plt.title("Ajuste modelo árboles de decisión")
plt.xlabel("Fecha")
plt.ylabel("Irradiancia")
plt.legend()
plt.show()

Análisis de residuales:

# Calcular los residuales sobre el conjunto de entrenamiento
residuals_train = y_train - y_pred_train

# Configuración de la figura para los subplots
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(14, 6))

# Gráfico de valores predichos vs. valores reales
axs[0].scatter(y_pred_train, y_train, color="blue", alpha=0.5)
axs[0].plot(
    [y_train.min(), y_train.max()], [y_train.min(), y_train.max()], "k--", lw=2
)  # Línea diagonal ideal
axs[0].set_title("Valores Reales vs. Valores Predichos (Train)")
axs[0].set_xlabel("Valores Predichos")
axs[0].set_ylabel("Valores Reales")

# Gráfico de residuales
axs[1].scatter(
    np.arange(len(residuals_train)), residuals_train, color="purple", alpha=0.3
)
axs[1].axhline(y=0, color="black", linestyle="--")  # Línea en y=0 para referencia
axs[1].set_title("Gráfico de Residuales (Train)")
axs[1].set_xlabel("Índice")
axs[1].set_ylabel("Residuales")

# Mejorar el layout para evitar solapamientos
plt.tight_layout()

# Mostrar la figura
plt.show()

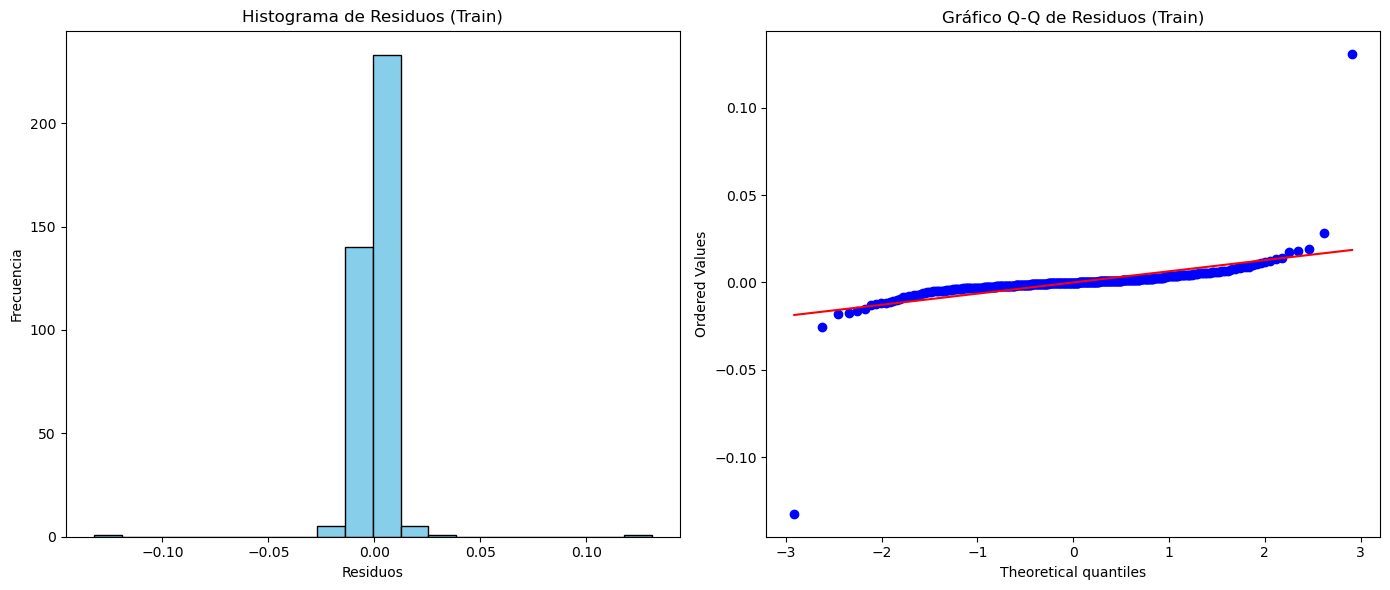
# Visualización del histograma de los residuos
plt.figure(figsize=(14, 6))

plt.subplot(1, 2, 1)
plt.hist(residuals_train, bins=20, color="skyblue", edgecolor="black")
plt.title("Histograma de Residuos (Train)")
plt.xlabel("Residuos")
plt.ylabel("Frecuencia")

# Visualización del gráfico Q-Q de los residuos
plt.subplot(1, 2, 2)
stats.probplot(residuals_train, dist="norm", plot=plt)
plt.title("Gráfico Q-Q de Residuos (Train)")

# Ajustar el diseño de la figura
plt.tight_layout()

# Mostrar la figura
plt.show()

Predicciones fuera de la muestra:

# Tomar el último valor de X_test como punto de partida para las predicciones fuera de muestra
last_X = X_test.iloc[-1].values.reshape(1, -1)


# Número de pasos adelante para predecir
n_steps_ahead = 12 * 5

# Array para almacenar las predicciones fuera de muestra
predictions_out_of_sample = []

for _ in range(n_steps_ahead):
    # Hacer la predicción usando el último valor de X
    pred = best_xgb_model.predict(last_X)

    # Guardar la predicción
    predictions_out_of_sample.append(pred[0])

    # Crear la nueva entrada para la siguiente predicción
    # Aquí se utiliza la predicción actual como la siguiente entrada
    last_X = np.array(pred).reshape(1, -1)

# Crear un rango de fechas para las predicciones fuera de muestra
dates_out_of_sample = pd.date_range(
    start=y_test.index[-1], periods=n_steps_ahead + 1, freq="M"
)[1:]

# Graficar las predicciones fuera de muestra
plt.figure(figsize=(10, 6))
plt.plot(y_test.index, y_test, label="Datos Reales (Test)")
plt.plot(
    dates_out_of_sample,
    predictions_out_of_sample,
    label="Predicciones Fuera de Muestra",
    color="red",
    linestyle="--",
)
plt.title("Predicciones Fuera de Muestra con Árbol de Decisión")
plt.xlabel("Fecha")
plt.ylabel("Valores Predichos")
plt.legend()
plt.show()

Lags de la serie de tiempo como variables de entrada:

# Crear características de lags
n_lags = 3  # Número de lags que deseas utilizar

data_lags = data.copy()
for lag in range(1, n_lags + 1):
    data_lags[f"Irradiancia_Lag_{lag}"] = data["Irradiancia"].shift(lag)

# Eliminar las filas con valores NaN resultantes de los lags
data_lags.dropna(inplace=True)

# Separar características (X) y la variable objetivo (y)
X_lags = data_lags.drop(columns=["Irradiancia"])
y_lags = data_lags["Irradiancia"]

X_train_lags, X_test_lags, y_train_lags, y_test_lags = train_test_split(
    X_lags, y_lags, test_size=0.2, shuffle=False, random_state=34
)

# Crear el modelo de XGBoost para regresión
xgboost_regressor = xgb.XGBRegressor(objective="reg:squarederror", random_state=34)

# Definir el espacio de hiperparámetros
param_dist = {
    "n_estimators": np.arange(100, 1000, 100),
    # Número de árboles en el modelo (también conocido como número de iteraciones de boosting).
    "max_depth": np.arange(3, 10, 1),
    # Profundidad máxima de cada árbol. Aumentar este valor hace que el modelo sea más complejo y más propenso al sobreajuste.
    "learning_rate": np.linspace(0.01, 0.3, 10),
    # Tasa de aprendizaje, que reduce la contribución de cada árbol individual para evitar el sobreajuste.
    "subsample": np.linspace(0.5, 1.0, 10),
    # Fracción de muestras utilizadas para entrenar cada árbol. Útil para reducir la varianza del modelo.
    "colsample_bytree": np.linspace(0.5, 1.0, 10),
    # Fracción de características seleccionadas al azar para entrenar cada árbol. Ayuda a reducir la correlación entre árboles.
    "gamma": np.linspace(0, 0.5, 5),
    # Mínima reducción de la pérdida necesaria para hacer una división adicional en un nodo del árbol. Mayor gamma significa árboles más conservadores.
    "reg_alpha": np.linspace(0, 1, 10),
    # Término de regularización L1 (Lasso). Controla la complejidad del modelo penalizando los pesos grandes.
    "reg_lambda": np.linspace(0, 1, 10)
    # Término de regularización L2 (Ridge). También controla la complejidad del modelo, pero penaliza los pesos en función de su magnitud cuadrática.
}


# Configurar RandomizedSearchCV
random_search_lags = RandomizedSearchCV(
    estimator=xgboost_regressor,
    param_distributions=param_dist,
    n_iter=500,  # Número de combinaciones aleatorias a evaluar
    scoring="neg_mean_squared_error",
    cv=5,
    verbose=2,
    random_state=34,
    n_jobs=-1,  # Usar todos los núcleos disponibles
)

# Ajustar RandomizedSearchCV al conjunto de entrenamiento
random_search_lags.fit(X_train_lags, y_train_lags)

# Obtener el mejor modelo
best_xgb_model_lags = random_search_lags.best_estimator_

# Entrenar el modelo de XGBoost con los datos de entrenamiento
best_xgb_model_lags = best_xgb_model_lags.fit(X_train_lags, y_train_lags)

print("Mejores hiperparámetros encontrados: ", random_search_lags.best_params_)

Fitting 5 folds for each of 500 candidates, totalling 2500 fits
Mejores hiperparámetros encontrados:  {'subsample': 1.0, 'reg_lambda': 0.3333333333333333, 'reg_alpha': 0.0, 'n_estimators': 500, 'max_depth': 3, 'learning_rate': 0.1711111111111111, 'gamma': 0.5, 'colsample_bytree': 1.0}

Evaluación del modelo:

# Predecir los datos de entrenamiento:
y_pred_train_lags = best_xgb_model_lags.predict(X_train_lags)

# Predecir los datos de prueba:
y_pred_lags = best_xgb_model_lags.predict(X_test_lags)

## Calcular R² Score Train:
r2_train = r2_score(y_train_lags, y_pred_train_lags)
print("R² Score Train:", r2_train)

# Calcular R² Score Test:
r2_test = r2_score(y_test_lags, y_pred_lags)
print("R² Score Test:", r2_test)

R² Score Train: 0.5231961800761558
R² Score Test: 0.30645636650828023

# Gráfica de resultados
plt.figure(figsize=(14, 7))
plt.plot(y_test_lags.index, y_test_lags.values, label="Test", color="green")
plt.plot(y_test_lags.index, y_pred_lags, label="Predicted", linestyle="--", color="red")
plt.title("Ajuste modelo árboles de decisión")
plt.xlabel("Fecha")
plt.ylabel("Irradiancia")
plt.legend()
plt.show()

Análisis de los residuales:

# Calcular los residuales sobre el conjunto de entrenamiento
residuals_train = y_train_lags - y_pred_train_lags

# Configuración de la figura para los subplots
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(14, 6))

# Gráfico de valores predichos vs. valores reales
axs[0].scatter(y_pred_train_lags, y_train_lags, color="blue", alpha=0.5)
axs[0].plot(
    [y_train.min(), y_train.max()], [y_train.min(), y_train.max()], "k--", lw=2
)  # Línea diagonal ideal
axs[0].set_title("Valores Reales vs. Valores Predichos (Train)")
axs[0].set_xlabel("Valores Predichos")
axs[0].set_ylabel("Valores Reales")

# Gráfico de residuales
axs[1].scatter(y_train_lags.index, residuals_train, color="purple", alpha=0.3)
axs[1].axhline(y=0, color="black", linestyle="--")  # Línea en y=0 para referencia
axs[1].set_title("Gráfico de Residuales (Train)")
axs[1].set_xlabel("Tiempo")
axs[1].set_ylabel("Residuales")

# Mejorar el layout para evitar solapamientos
plt.tight_layout()

# Mostrar la figura
plt.show()

# Visualización del histograma de los residuos
plt.figure(figsize=(14, 6))

plt.subplot(1, 2, 1)
plt.hist(residuals_train, bins=20, color="skyblue", edgecolor="black")
plt.title("Histograma de Residuos (Train)")
plt.xlabel("Residuos")
plt.ylabel("Frecuencia")

# Visualización del gráfico Q-Q de los residuos
plt.subplot(1, 2, 2)
stats.probplot(residuals_train, dist="norm", plot=plt)
plt.title("Gráfico Q-Q de Residuos (Train)")

# Ajustar el diseño de la figura
plt.tight_layout()

# Mostrar la figura
plt.show()

Predicciones fuera de la muestra:

# Preparar el punto de partida (última fila de X_test)
last_X_lags = X_test_lags.iloc[-1].values.reshape(1, -1)

# Número de pasos adelante para predecir
n_steps_ahead = 12 * 5

# Lista para almacenar las predicciones fuera de muestra
predictions_out_of_sample = []

for _ in range(n_steps_ahead):
    # Hacer la predicción usando el último valor de X
    pred = best_xgb_model_lags.predict(last_X_lags)

    # Guardar la predicción
    predictions_out_of_sample.append(pred[0])

    # Crear la nueva entrada para la siguiente predicción utilizando los lags
    new_X = np.roll(last_X_lags, shift=-1)  # Desplazar valores
    new_X[0, -n_lags:] = pred  # Actualizar con la nueva predicción
    last_X_lags = new_X.reshape(1, -1)  # Reajustar la forma

# Crear un rango de fechas para las predicciones fuera de muestra
dates_out_of_sample = pd.date_range(
    start=y_test.index[-1], periods=n_steps_ahead + 1, freq="M"
)[1:]

# Graficar las predicciones fuera de muestra
plt.figure(figsize=(10, 6))
plt.plot(y_test_lags.index, y_test_lags, label="Datos reales (Test)")
plt.plot(
    dates_out_of_sample,
    predictions_out_of_sample,
    label="Predicciones fuera de muestra",
    color="red",
    linestyle="--",
)
plt.title("Predicciones fuera de muestra con Random Forest (con Lags)")
plt.xlabel("Fecha")
plt.ylabel("Valores Predichos")
plt.legend()
plt.show()