Preprocesamiento de datos#
El preprocesamiento de datos es una etapa crucial en el desarrollo de modelos de Machine Learning. Implica preparar y transformar los datos en un formato adecuado para que los algoritmos de aprendizaje puedan extraer patrones y conocimientos valiosos. Este proceso incluye la manipulación y limpieza de datos, la transformación de variables, la gestión de valores faltantes y la partición de los datos en conjuntos de entrenamiento y prueba.
Tipos datos:#
Los datos pueden clasificarse en diferentes tipos según sus características y la naturaleza de sus valores. A continuación, se describen los principales tipos de datos:
Variables continuas:
Las variables continuas son aquellas que pueden tomar cualquier valor numérico dentro de un rango específico, incluyendo decimales. Estas variables suelen representar medidas cuantitativas y pueden asumir cualquier valor real positivo o negativo. Ejemplos comunes de variables continuas incluyen el peso (por ejemplo, 70,25 kg), la altura, el tiempo y la temperatura. Son fundamentales en el análisis estadístico debido a su capacidad para capturar variaciones detalladas.
Variables discretas:
Las variables discretas son aquellas que solo pueden asumir valores específicos y finitos dentro de un conjunto determinado. Estas variables suelen ser enteras y no permiten valores intermedios entre dos valores sucesivos. Un ejemplo típico de una variable discreta es el número de habitantes en un barrio o el número de la comuna al que pertenece un barrio. Aunque estas variables pueden ser numéricas, su orden no necesariamente influye en el análisis; es decir, un número mayor no implica mayor importancia o significado.
Datos nominales:
Los datos nominales son un tipo de datos categóricos que no tienen un orden intrínseco ni permiten una comparación cuantitativa. Pueden tomar valores no numéricos que representan categorías o etiquetas distintivas. Por ejemplo, nombres, direcciones, géneros (masculino, femenino) y colores son atributos de datos nominales. En el análisis estadístico, la moda es la única medida de tendencia central aplicable, ya que las operaciones aritméticas no tienen sentido para estos datos.
Datos ordinales:
Los datos ordinales son un tipo de datos categóricos en los que existe un orden o jerarquía inherente entre los valores. Aunque no cuantifican la diferencia exacta entre valores, permiten establecer comparaciones relativas como “mayor que” o “menor que”. Ejemplos de datos ordinales incluyen las tallas de camisetas (S, M, L, XL) y las escalas de Likert en encuestas (Siempre, A veces, Rara vez, Nunca). La mediana es una medida adecuada de tendencia central para los datos ordinales.
DataTypes1#
Escalado de variables:#
El escalado de variables, también conocido como feature scaling, es una transformación crucial en el preprocesamiento de datos, especialmente cuando las variables numéricas tienen diferentes escalas. Algunos algoritmos de Machine Learning, como SVM y kNN, son sensibles a las escalas de las variables y pueden verse afectados negativamente si no se aplican técnicas de escalado.
Existen dos enfoques comunes para escalar variables:
1. Escalado Min-Max (Normalización):
El escalado Min-Max transforma los valores de las variables para que se encuentren dentro de un rango específico, generalmente entre 0 y 1. Esta técnica reescala los valores en función de los valores mínimo y máximo observados en los datos. La fórmula para el escalado Min-Max es:
Donde \(𝑋_𝑖\) es el valor original, \(𝑋_{𝑚𝑖𝑛}\) es el valor mínimo y \(𝑋_{𝑚𝑎𝑥}\) es el valor máximo. Esta técnica es útil cuando se desea conservar la interpretación relativa de los valores originales.
2. Estandarización (Z-score Normalization):
La estandarización, o normalización Z-score, transforma los valores de las variables para que tengan una media de cero y una desviación estándar de uno. Esto permite que las variables tengan una distribución normalizada. La fórmula para la estandarización es:
Donde \(\mu\) es la media y \(s\) la desviación estándar de las muestras.
La estandarización es menos sensible a los valores atípicos que el escalado Min-Max y es preferida en situaciones donde se desea una distribución normalizada.
Nota: Es importante ajustar los escaladores solo al conjunto de datos de entrenamiento y luego aplicar la transformación a los conjuntos de validación y prueba. Esto evita introducir sesgos en el modelo.
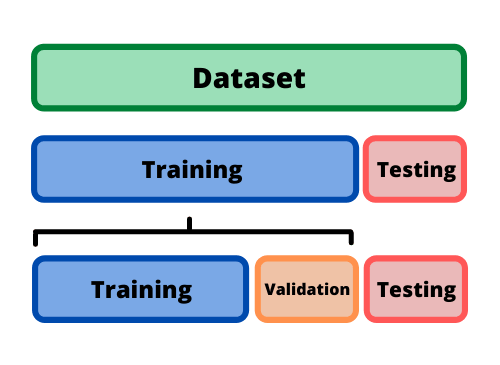
Conjunto de entrenamiento (train) y conjunto de prueba (test):#
La evaluación adecuada del modelo es esencial antes de implementarlo en un entorno de producción. Para garantizar que el modelo funcione bien con nuevos datos, se debe dividir el dataset en dos conjuntos: el conjunto de entrenamiento y el conjunto de prueba.
Conjunto de entrenamiento (Training Set):
El conjunto de entrenamiento se utiliza para ajustar los parámetros del modelo y los hiperparámetros. Durante el entrenamiento, el modelo aprende a partir de los datos para minimizar el error de predicción. Este conjunto suele representar la mayoría del dataset y se utiliza para construir y ajustar el modelo.
Conjunto de prueba (Test Set):
El conjunto de prueba se utiliza para evaluar el rendimiento del modelo en datos que no ha visto durante el entrenamiento. Este conjunto es crucial para medir la capacidad de generalización del modelo. La tasa de error en el conjunto de prueba se conoce como error de generalización o error fuera de la muestra. Un alto error de generalización indica que el modelo puede no funcionar bien con datos nuevos.
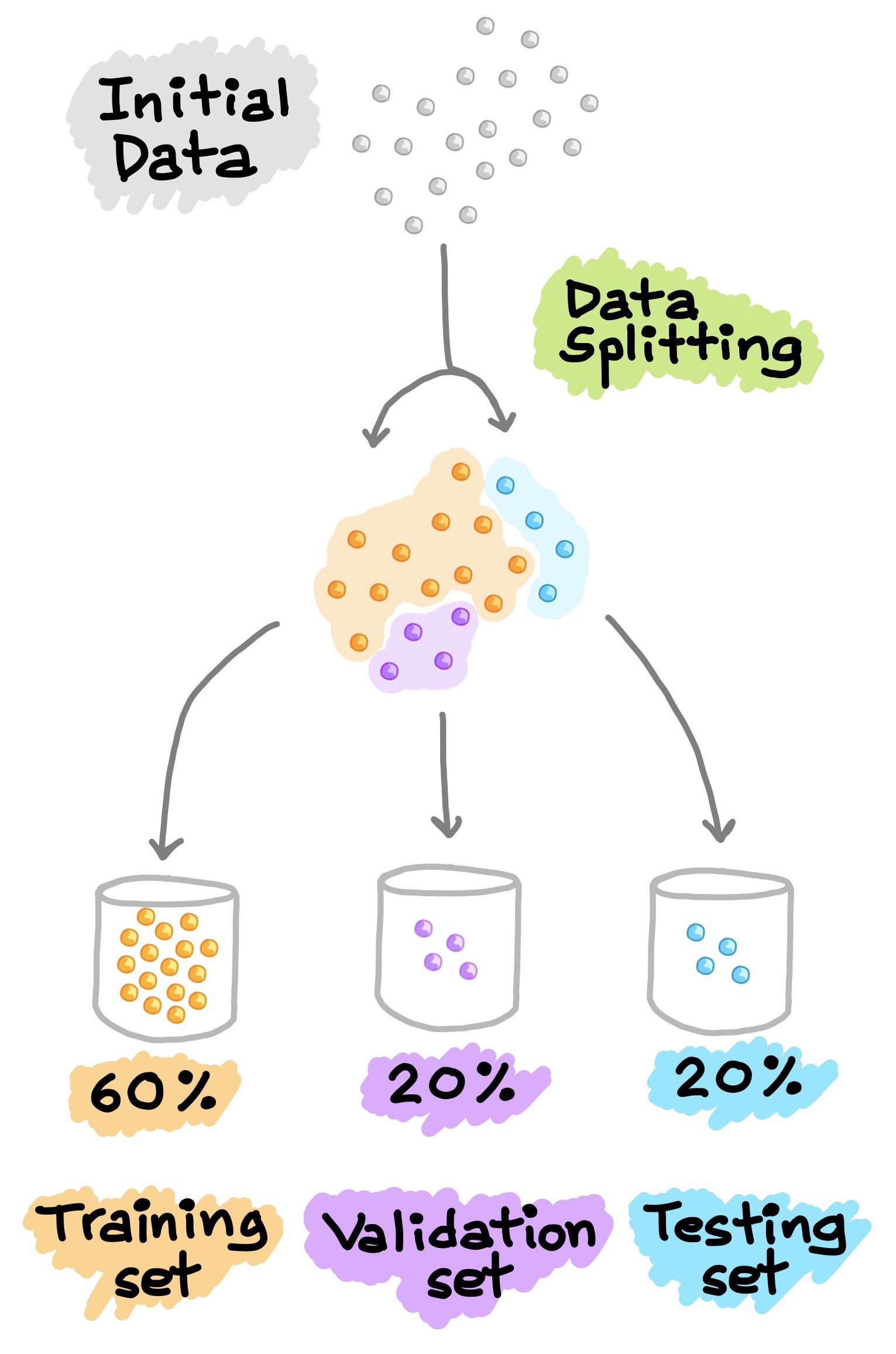
Consideraciones sobre la división del Dataset:
Una división común es utilizar el 80% del dataset para entrenamiento y el 20% restante para prueba.
La proporción exacta puede variar según el tamaño del dataset; en datasets muy grandes, incluso un 1% de datos para prueba puede ser suficiente para una evaluación confiable.
El sobreajuste (overfitting) ocurre cuando el error en el conjunto de entrenamiento es bajo, pero el error en el conjunto de prueba es alto, lo que indica que el modelo ha aprendido patrones específicos del conjunto de entrenamiento que no generalizan bien.
DataSet#
DataSetSplit#