Backtesting método VaR Simulación Monte Carlo¶

Importar datos.¶

datos = read.csv("Tres acciones.csv", sep = ";")

Matriz de precios.¶

precios = datos[,-1]

Proporciones de inversión.¶

proporciones = c(0.25,0.5,0.25)

Matriz de rendimientos.¶

rendimientos = matrix(, nrow(precios)-1, ncol(precios))

for(i in 1:ncol(precios)){

  rendimientos[,i] = diff(log(precios[,i]))
}

Rendimientos portafolio de inversión¶

rendimientos_portafolio = vector()

for(i in 1:nrow(rendimientos)){

  rendimientos_portafolio[i] = sum(rendimientos[i,]*proporciones)
}

Ventana para Backtesting¶

ventana_backtesting = 250

rendimientos_backtesting = matrix(, ventana_backtesting, ncol(rendimientos))

for(i in 1:ncol(rendimientos)){

rendimientos_backtesting[,i] = rendimientos[-c(nrow(rendimientos)-ventana_backtesting:nrow(rendimientos)), i]
}

#Para el portafolio de Inversión

rendimientos_backtesting_portafolio = rendimientos_portafolio[-c(nrow(rendimientos)-ventana_backtesting:nrow(rendimientos))]

Backtesting método VaR Simulación Monte Carlo (NC = 95% y H = 250)¶

Se realizará el Backtesting con una ventana de 250 y nivel de confianza del 95%.

NC = 0.95

Volatilidad histórica y rendimiento medio (NC = 95% y H = 250)¶

volatilidad_historica = matrix(, ventana_backtesting, ncol(rendimientos))

rendimiento_medio = matrix(, ventana_backtesting, ncol(rendimientos))

for(j in 1:ncol(rendimientos)){

  for(i in 1:ventana_backtesting){

    volatilidad_historica[i,j] = sd(rendimientos[1:(nrow(rendimientos)-ventana_backtesting+i), j])

    rendimiento_medio[i,j] = mean(rendimientos[1:(nrow(rendimientos)-ventana_backtesting+i), j])
 }
}

Rendimientos simulados de cada acción para ventana Backtesting (NC = 95% y H = 250)¶

iteraciones = 50000

dt = 1

st = matrix(, ventana_backtesting, ncol(rendimientos))

for(i in 1:ncol(rendimientos)){

    st[,i] = tail(precios[,i], ventana_backtesting)
}

rend_backtesting = array(dim = c(ventana_backtesting, iteraciones, ncol(rendimientos)))

aleatorio_corr = vector()

for(k in 1:ncol(rendimientos)){

    for(i in 1:ventana_backtesting){

        correlacion = cor(rendimientos[1:(nrow(rendimientos)-ventana_backtesting+i),])

        cholesky = chol(correlacion)

    for(j in 1:iteraciones){

        aleatorio = rnorm(ncol(rendimientos))

        aleatorio_corr = colSums(aleatorio*cholesky)

        rend_backtesting[i,j,k] = st[i,k]*exp((rendimiento_medio[i,k]-volatilidad_historica[i,k]^2/2)*dt+volatilidad_historica[k]*sqrt(dt)*aleatorio_corr[k])/st[i,k]-1

}}}

VaR Simulación Monte Carlo para Backtesting (NC = 95% y H = 250)¶

VaR_individuales_SM_percentil = matrix(, ventana_backtesting, ncol(rendimientos))

for(j in 1:ncol(rendimientos)){

  for(i in 1:ventana_backtesting){

    VaR_individuales_SM_percentil[i,j] = abs(quantile(rend_backtesting[i,,j], 1-NC))
  }
}

plot(rendimientos_backtesting[,1], t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "ECO")
lines(-VaR_individuales_SM_percentil[,1], t = "l", col = "darkred")
legend("topright","VaR Simulación Monte Carlo", lty = 1, col = "darkred")

plot(rendimientos_backtesting[,2], t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "PFBCOLOM")
lines(-VaR_individuales_SM_percentil[,2], t = "l", col = "darkred")
legend("topright","VaR Simulación Monte Carlo", lty = 1, col = "darkred")

plot(rendimientos_backtesting[,3], t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "ISA")
lines(-VaR_individuales_SM_percentil[,3], t = "l", col = "darkred")
legend("topright","VaR Simulación Monte Carlo", lty = 1, col = "darkred")

Excepciones VaR Simulación Monte Carlo (NC = 95% y H = 250)¶

excepciones_SM_percentil = vector()

for(j in 1:ncol(rendimientos)){

  excepciones_SM_percentil[j]=0

  for(i in 1:ventana_backtesting){

      ifelse(-VaR_individuales_SM_percentil[i,j] > rendimientos_backtesting[i,j], excepciones_SM_percentil[j] <- excepciones_SM_percentil[j]+1, excepciones_SM_percentil[j] <- excepciones_SM_percentil[j])
}}

p.gorro_SM_percentil=excepciones_SM_percentil/ventana_backtesting

excepciones_SM_percentil

p.gorro_SM_percentil

17
4
9

0.068
0.016
0.036

En el método VaR Simulación Monte Carlo se hallaron 17 exepciones en la acción de ECO, 4 en PFBCOLOM y 9 en ISA. Que corresponde a un 6,8%, 1,6% y 3,6%, respectivamente.

Como el nivel de confianza es del 95%, se espera una proporción de exepción aproximada al 5% en cada de las acciones.

Con las proporciones de exepción mayores al 5% aparentemente el VaR está subvalornado el riesgo porque el método de VaR implementado está cubriendo más porcentaje de las pérdidas cuanto está diseñado para un cubrimiento del 5% (α).

Sin embargo, se aconseja realizar más pruebas de Backtesting para determinar si el método empleado es adecuado. El siguiente método de Backtesting tiene como insumo las proporciones de exepción $𝑝 ̂ $.

Prueba de Kupiec VaR Simulación Monte Carlo (NC = 95% y H = 250)¶

tu_SM_percentil = (p.gorro_SM_percentil-(1-NC))/sqrt(p.gorro_SM_percentil*(1-p.gorro_SM_percentil)/ventana_backtesting)

tu_critico = abs(qt((1-NC)/2,ventana_backtesting-1))

aprobados_SM_percentil = vector()

for(i in 1:ncol(rendimientos)){

  aprobados_SM_percentil[i] = ifelse(abs(tu_SM_percentil[i]) < tu_critico,aprobados_SM_percentil[i]<-1, aprobados_SM_percentil[i] <- 0)

}

aprobados_SM_percentil

1
0
1

Con con una ventana de 250 y nivel de confianza del 95% el método de VaR Simulación Monte Carlo se acepta para las acciones ECO e ISA y se rechaza para PFBCOLOM.

Rendimientos diarios simulados para Backtesting del portafolio (NC = 95% y H = 250)¶

rend_port_backtesting = matrix(, ventana_backtesting, iteraciones)

for(j in 1:iteraciones){

    for(i in 1:ventana_backtesting){

    rend_port_backtesting[i,j] = sum(rend_backtesting[i,j,]*proporciones)
}}

VaR Simulación Monte Carlo para Backtesting del portafolio (NC = 95% y H = 250)¶

VaR_portafolio_SM_percentil = vector()

  for(i in 1:ventana_backtesting){

    VaR_portafolio_SM_percentil[i] = abs(quantile(rend_port_backtesting[i,], 1-NC))
}

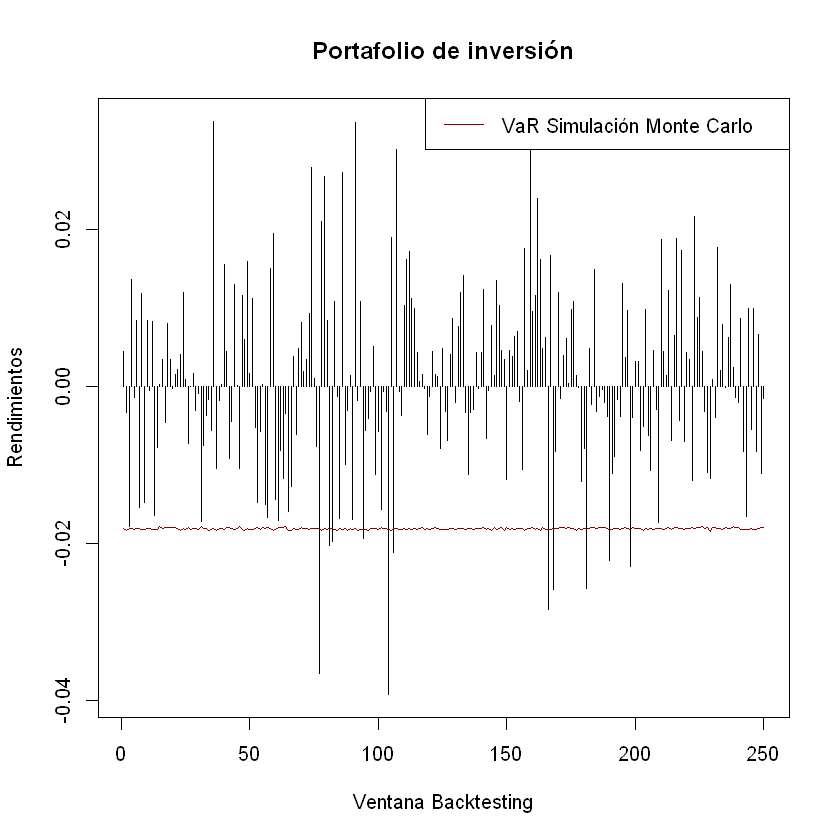
plot(rendimientos_backtesting_portafolio, t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "Portafolio de inversión")
lines(-VaR_portafolio_SM_percentil, t = "l", col = "darkred")
legend("topright","VaR Simulación Monte Carlo", lty = 1, col = "darkred")

Excepciones VaR Simulación Monte Carlo del portafolio (NC = 95% y H = 250)¶

excepciones_SM_percentil_portafolio = 0

  for(i in 1:ventana_backtesting){

      ifelse(-VaR_portafolio_SM_percentil[i] > rendimientos_backtesting_portafolio[i], excepciones_SM_percentil_portafolio <- excepciones_SM_percentil_portafolio+1, excepciones_SM_percentil_portafolio <- excepciones_SM_percentil_portafolio)
}

p.gorro_SM_percentil_portafolio = excepciones_SM_percentil_portafolio/ventana_backtesting

excepciones_SM_percentil_portafolio

p.gorro_SM_percentil_portafolio

110.044

Prueba de Kupiec VaR Simulación Monte Carlo (NC = 95% y H = 250)¶

tu_SM_percentil_portafolio = (p.gorro_SM_percentil_portafolio-(1-NC))/sqrt(p.gorro_SM_percentil_portafolio*(1-p.gorro_SM_percentil_portafolio)/ventana_backtesting)

tu_critico = abs(qt((1-NC)/2, ventana_backtesting-1))

aprobados_SM_percentil_portafolio = ifelse(abs(tu_SM_percentil_portafolio) < tu_critico,aprobados_SM_percentil_portafolio <- 1, aprobados_SM_percentil_portafolio <- 0)

aprobados_SM_percentil_portafolio

1

Conclusión:¶

Con con una ventana de 250 y nivel de confianza del 95%, el método de VaR Simulación Monte Carlo es aceptado para las acciones de ECO e ISA y para el portafolio de inversión. En cambio, es rechazado para la acción PFBCOLOM.

Backtesting método VaR Simulación Monte Carlo (NC = 99% y H = 250)¶

Se realizará el Backtesting con una ventana de 250 y nivel de confianza del 99%.

NC = 0.99

En el código anterior se realizó la simulación de los rendimientos para una ventana de 250 de las tres acciones y del portafolio de inversión, por lo que no es necesario volverla hacer.

VaR Simulación Monte Carlo para Backtesting (NC = 99% y H = 250)¶

VaR_individuales_SM_percentil = matrix(, ventana_backtesting, ncol(rendimientos))

for(j in 1:ncol(rendimientos)){

  for(i in 1:ventana_backtesting){

    VaR_individuales_SM_percentil[i,j] = abs(quantile(rend_backtesting[i,,j], 1-NC))
  }
}

Excepciones VaR Simulación Monte Carlo (NC = 99% y H = 250)¶

excepciones_SM_percentil = vector()

for(j in 1:ncol(rendimientos)){

  excepciones_SM_percentil[j] = 0

  for(i in 1:ventana_backtesting){

      ifelse(-VaR_individuales_SM_percentil[i,j] > rendimientos_backtesting[i,j], excepciones_SM_percentil[j] <- excepciones_SM_percentil[j]+1, excepciones_SM_percentil[j] <- excepciones_SM_percentil[j])
}}

p.gorro_SM_percentil = excepciones_SM_percentil/ventana_backtesting

excepciones_SM_percentil

p.gorro_SM_percentil

9
0
2

0.036
0
0.008

En el método VaR Simulación Monte Carlo se hallaron 8 exepciones en la acción de ECO, 0 en PFBCOLOM y 2 en ISA. Que corresponde a un 3,2%, 0% y 0,8%, respectivamente.

Prueba de Kupiec VaR Simulación Monte Carlo (NC = 99% y H = 250)¶

tu_SM_percentil = (p.gorro_SM_percentil-(1-NC))/sqrt(p.gorro_SM_percentil*(1-p.gorro_SM_percentil)/ventana_backtesting)

tu_critico = abs(qt((1-NC)/2, ventana_backtesting-1))

aprobados_SM_percentil = vector()

for(i in 1:ncol(rendimientos)){

  aprobados_SM_percentil[i] = ifelse(abs(tu_SM_percentil[i]) < tu_critico,aprobados_SM_percentil[i] <- 1, aprobados_SM_percentil[i] <- 0)

}

aprobados_SM_percentil

1
0
1

Con con una ventana de 250 y nivel de confianza del 99% el método de VaR Simulación Monte Carlo se acepta para las acciones ECO e ISA y se rechaza para PFBCOLOM.

VaR Simulación Monte Carlo para Backtesting del portafolio (NC = 99% y H = 250)¶

VaR_portafolio_SM_percentil = vector()

  for(i in 1:ventana_backtesting){

    VaR_portafolio_SM_percentil[i] = abs(quantile(rend_port_backtesting[i,], 1-NC))
}

Excepciones VaR Simulación Monte Carlo del portafolio (NC = 99% y H = 250)¶

excepciones_SM_percentil_portafolio = 0

  for(i in 1:ventana_backtesting){

      ifelse(-VaR_portafolio_SM_percentil[i] > rendimientos_backtesting_portafolio[i], excepciones_SM_percentil_portafolio <- excepciones_SM_percentil_portafolio+1,excepciones_SM_percentil_portafolio <- excepciones_SM_percentil_portafolio)
}

p.gorro_SM_percentil_portafolio = excepciones_SM_percentil_portafolio/ventana_backtesting

excepciones_SM_percentil_portafolio

p.gorro_SM_percentil_portafolio

50.02

Prueba de Kupiec VaR Simulación Monte Carlo (NC = 99% y H = 250)¶

tu_SM_percentil_portafolio = (p.gorro_SM_percentil_portafolio-(1-NC))/sqrt(p.gorro_SM_percentil_portafolio*(1-p.gorro_SM_percentil_portafolio)/ventana_backtesting)

tu_critico = abs(qt((1-NC)/2, ventana_backtesting-1))

aprobados_SM_percentil_portafolio = ifelse(abs(tu_SM_percentil_portafolio) < tu_critico, aprobados_SM_percentil_portafolio <- 1, aprobados_SM_percentil_portafolio <- 0)

aprobados_SM_percentil_portafolio

1

Conclusión:¶

Con con una ventana de 250 y nivel de confianza del 99%, el método de VaR Simulación Monte Carlo es aceptado para las acciones de ECO e ISA y para el portafolio de inversión. En cambio, es rechazado para la acción PFBCOLOM.

Backtesting método VaR Simulación Monte Carlo (NC = 99% y H = 500)¶

Se realizará el Backtesting con una ventana de 500 y nivel de confianza del 99%.

NC = 0.99

Ventana para Backtesting¶

ventana_backtesting = 500

rendimientos_backtesting = matrix(, ventana_backtesting, ncol(rendimientos))

for(i in 1:ncol(rendimientos)){

rendimientos_backtesting[,i] = rendimientos[-c(nrow(rendimientos)-ventana_backtesting:nrow(rendimientos)), i]
}

#Para el portafolio de Inversión

rendimientos_backtesting_portafolio = rendimientos_portafolio[-c(nrow(rendimientos)-ventana_backtesting:nrow(rendimientos))]

Se debe simular los rendimientos de las tres acciones y del portafolio de inversión para una ventana de 500 porque en el código anterior se realizó con una ventana de 250. Por tanto, también se debe calcular las volatilidades históricas y rendimientos medios para la ventana de 500.

Volatilidad histórica y rendimiento medio (NC = 99% y H = 500)¶

volatilidad_historica = matrix(, ventana_backtesting, ncol(rendimientos))

rendimiento_medio = matrix(, ventana_backtesting, ncol(rendimientos))

for(j in 1:ncol(rendimientos)){

  for(i in 1:ventana_backtesting){

    volatilidad_historica[i,j] = sd(rendimientos[1:(nrow(rendimientos)-ventana_backtesting+i), j])

    rendimiento_medio[i,j] = mean(rendimientos[1:(nrow(rendimientos)-ventana_backtesting+i), j])
 }
}

Rendimientos simulados de cada acción para ventana Backtesting (NC = 99% y H = 500)¶

iteraciones = 50000

dt = 1

st = matrix(, ventana_backtesting, ncol(rendimientos))

for(i in 1:ncol(rendimientos)){

    st[,i] = tail(precios[,i], ventana_backtesting)
}

rend_backtesting=array(dim=c(ventana_backtesting,iteraciones,ncol(rendimientos)))

aleatorio_corr=vector()

for(k in 1:ncol(rendimientos)){

    for(i in 1:ventana_backtesting){

        correlacion = cor(rendimientos[1:(nrow(rendimientos)-ventana_backtesting+i),])

        cholesky = chol(correlacion)

    for(j in 1:iteraciones){

        aleatorio = rnorm(ncol(rendimientos))

        aleatorio_corr = colSums(aleatorio*cholesky)

        rend_backtesting[i,j,k] = st[i,k]*exp((rendimiento_medio[i,k]-volatilidad_historica[i,k]^2/2)*dt+volatilidad_historica[k]*sqrt(dt)*aleatorio_corr[k])/st[i,k]-1

}}}

VaR Simulación Monte Carlo para Backtesting (NC = 99% y H = 500)¶

VaR_individuales_SM_percentil = matrix(, ventana_backtesting, ncol(rendimientos))

for(j in 1:ncol(rendimientos)){

  for(i in 1:ventana_backtesting){

    VaR_individuales_SM_percentil[i,j] = abs(quantile(rend_backtesting[i,,j], 1-NC))
  }
}

Excepciones VaR Simulación Monte Carlo (NC = 99% y H = 500)¶

excepciones_SM_percentil = vector()

for(j in 1:ncol(rendimientos)){

  excepciones_SM_percentil[j] = 0

  for(i in 1:ventana_backtesting){

      ifelse(-VaR_individuales_SM_percentil[i,j] > rendimientos_backtesting[i,j], excepciones_SM_percentil[j] <- excepciones_SM_percentil[j]+1, excepciones_SM_percentil[j] <- excepciones_SM_percentil[j])
}}

p.gorro_SM_percentil = excepciones_SM_percentil/ventana_backtesting

excepciones_SM_percentil

p.gorro_SM_percentil

15
1
3

0.03
0.002
0.006

En el método VaR Simulación Monte Carlo se hallaron 14 exepciones en la acción de ECO, 1 en PFBCOLOM y 3 en ISA. Que corresponde a un 2,8%. 0,2% y 0,6%, respectivamente.

Prueba de Kupiec VaR Simulación Monte Carlo (NC = 99% y H = 500)¶

tu_SM_percentil = (p.gorro_SM_percentil-(1-NC))/sqrt(p.gorro_SM_percentil*(1-p.gorro_SM_percentil)/ventana_backtesting)

tu_critico = abs(qt((1-NC)/2, ventana_backtesting-1))

aprobados_SM_percentil = vector()

for(i in 1:ncol(rendimientos)){

  aprobados_SM_percentil[i] = ifelse(abs(tu_SM_percentil[i]) < tu_critico,aprobados_SM_percentil[i] <- 1, aprobados_SM_percentil[i] <- 0)
}

aprobados_SM_percentil

0
0
1

Con con una ventana de 500 y nivel de confianza del 99% el método de VaR Simulación Monte Carlo se acepta para las acciones ECO e ISA y se rechaza para PFBCOLOM.

Rendimientos diarios simulados para Backtesting del portafolio (NC = 99% y H = 500)¶

rend_port_backtesting = matrix(, ventana_backtesting, iteraciones)

for(j in 1:iteraciones){

    for(i in 1:ventana_backtesting){

    rend_port_backtesting[i,j] = sum(rend_backtesting[i,j,]*proporciones)
}}

VaR Simulación Monte Carlo para Backtesting del portafolio (NC = 99% y H = 500)¶

VaR_portafolio_SM_percentil = vector()

  for(i in 1:ventana_backtesting){

    VaR_portafolio_SM_percentil[i] = abs(quantile(rend_port_backtesting[i,], 1-NC))
}

Excepciones VaR Simulación Monte Carlo del portafolio (NC = 99% y H = 500)¶

excepciones_SM_percentil_portafolio = 0

  for(i in 1:ventana_backtesting){

      ifelse(-VaR_portafolio_SM_percentil[i] > rendimientos_backtesting_portafolio[i], excepciones_SM_percentil_portafolio <- excepciones_SM_percentil_portafolio+1, excepciones_SM_percentil_portafolio <- excepciones_SM_percentil_portafolio)
}

p.gorro_SM_percentil_portafolio = excepciones_SM_percentil_portafolio/ventana_backtesting

excepciones_SM_percentil_portafolio

p.gorro_SM_percentil_portafolio

100.02

Prueba de Kupiec VaR Simulación Monte Carlo (NC = 99% y H = 500)¶

tu_SM_percentil_portafolio = (p.gorro_SM_percentil_portafolio-(1-NC))/sqrt(p.gorro_SM_percentil_portafolio*(1-p.gorro_SM_percentil_portafolio)/ventana_backtesting)

tu_critico = abs(qt((1-NC)/2, ventana_backtesting-1))

aprobados_SM_percentil_portafolio = ifelse(abs(tu_SM_percentil_portafolio) < tu_critico, aprobados_SM_percentil_portafolio <- 1, aprobados_SM_percentil_portafolio <- 0)

aprobados_SM_percentil_portafolio

1

Conclusión:¶

Con con una ventana de 500 y nivel de confianza del 99%, el método de VaR Simulación Monte Carlo es aceptado para las acciones de ECO e ISA y para el portafolio de inversión. En cambio, es rechazado para la acción PFBCOLOM.

Backtesting método VaR Simulación Monte Carlo (NC = 95% y H = 500)¶

Se realizará el Backtesting con una ventana de 500 y nivel de confianza del 95%.

NC = 0.95

En el código anterior se realizó la simulación de los rendimientos para una ventana de 500 de las tres acciones y del portafolio de inversión, por lo que no es necesario volverla hacer.

VaR Simulación Monte Carlo para Backtesting (NC = 95% y H = 500)¶

VaR_individuales_SM_percentil = matrix(, ventana_backtesting, ncol(rendimientos))

for(j in 1:ncol(rendimientos)){

  for(i in 1:ventana_backtesting){

    VaR_individuales_SM_percentil[i,j] = abs(quantile(rend_backtesting[i,,j], 1-NC))
  }
}

Excepciones VaR Simulación Monte Carlo (NC = 95% y H = 500)¶

excepciones_SM_percentil = vector()

for(j in 1:ncol(rendimientos)){

  excepciones_SM_percentil[j] = 0

  for(i in 1:ventana_backtesting){

      ifelse(-VaR_individuales_SM_percentil[i,j] > rendimientos_backtesting[i,j], excepciones_SM_percentil[j] <- excepciones_SM_percentil[j]+1, excepciones_SM_percentil[j] <- excepciones_SM_percentil[j])
}}

p.gorro_SM_percentil = excepciones_SM_percentil/ventana_backtesting

excepciones_SM_percentil

p.gorro_SM_percentil

30
9
13

0.06
0.018
0.026

En el método VaR Simulación Monte Carlo se hallaron 14 exepciones en la acción de ECO, 1 en PFBCOLOM y 3 en ISA. Que corresponde a un 2,8%. 0,2% y 0,6%, respectivamente.

Prueba de Kupiec VaR Simulación Monte Carlo (NC = 95% y H = 500)¶

tu_SM_percentil = (p.gorro_SM_percentil-(1-NC))/sqrt(p.gorro_SM_percentil*(1-p.gorro_SM_percentil)/ventana_backtesting)

tu_critico = abs(qt((1-NC)/2, ventana_backtesting-1))

aprobados_SM_percentil = vector()

for(i in 1:ncol(rendimientos)){

  aprobados_SM_percentil[i] = ifelse(abs(tu_SM_percentil[i]) < tu_critico,aprobados_SM_percentil[i] <- 1, aprobados_SM_percentil[i] <- 0)
}

aprobados_SM_percentil

1
0
0

Con con una ventana de 250 y nivel de confianza del 95% el método de VaR Simulación Monte Carlo se acepta para las acciones ECO e ISA y se rechaza para PFBCOLOM.

VaR Simulación Monte Carlo para Backtesting del portafolio (NC = 95% y H = 500)¶

VaR_portafolio_SM_percentil = vector()

  for(i in 1:ventana_backtesting){

    VaR_portafolio_SM_percentil[i] = abs(quantile(rend_port_backtesting[i,], 1-NC))
}

Excepciones VaR Simulación Monte Carlo del portafolio (NC = 95% y H = 500)¶

excepciones_SM_percentil_portafolio = 0

  for(i in 1:ventana_backtesting){

      ifelse(-VaR_portafolio_SM_percentil[i] > rendimientos_backtesting_portafolio[i], excepciones_SM_percentil_portafolio <- excepciones_SM_percentil_portafolio+1, excepciones_SM_percentil_portafolio <- excepciones_SM_percentil_portafolio)
}

p.gorro_SM_percentil_portafolio = excepciones_SM_percentil_portafolio/ventana_backtesting

excepciones_SM_percentil_portafolio

p.gorro_SM_percentil_portafolio

210.042

Prueba de Kupiec VaR Simulación Monte Carlo (NC = 95% y H = 500)¶

tu_SM_percentil_portafolio = (p.gorro_SM_percentil_portafolio-(1-NC))/sqrt(p.gorro_SM_percentil_portafolio*(1-p.gorro_SM_percentil_portafolio)/ventana_backtesting)

tu_critico = abs(qt((1-NC)/2, ventana_backtesting-1))

aprobados_SM_percentil_portafolio = ifelse(abs(tu_SM_percentil_portafolio) < tu_critico,aprobados_SM_percentil_portafolio <- 1, aprobados_SM_percentil_portafolio <- 0)

aprobados_SM_percentil_portafolio

1

Conclusión:¶

Con con una ventana de 250 y nivel de confianza del 99%, el método de VaR Simulación Monte Carlo es aceptado para las acciones de ECO e ISA y para el portafolio de inversión. En cambio, es rechazado para la acción PFBCOLOM.

Conclusión general:¶

	ECO	PFBCOLOMB	ISA	Portafolio
NC = 95% y H = 250	Aceptado	Rechazado	Aceptado	Aceptado
NC = 95% y H = 500	Aceptado	Rechazado	Rechazado	Aceptado
NC = 99% y H = 250	Aceptado	Rechazado	Aceptado	Aceptado
NC = 99% y H = 500	Aceptado	Rechazado	Aceptado	Aceptado