Distribución normal

Función de Densidad de Probabilidad:

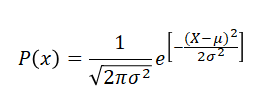
1

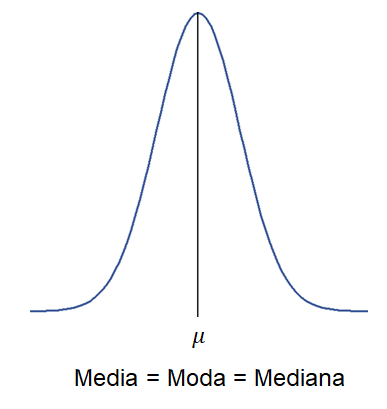
2

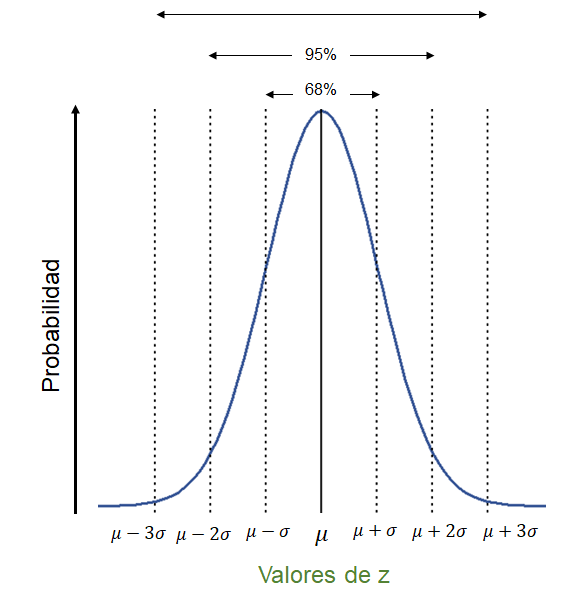
3

Distribución normal estándar.

\(\mu=0\) y \(\sigma^2=1\)

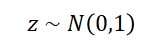
4

5

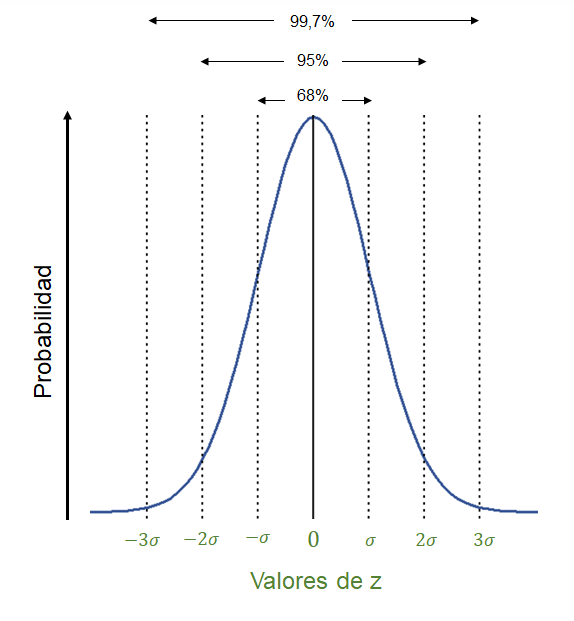
Ejemplo distribución normal estándar: \(\mu=0\) y \(\sigma^2=1\)

Se usa la función qnorm para hallar los valores de una distribución normal dada una probabilidad o percentil.

Con una probabilidad del 1% z es igual a -2,32634787404084.

z = qnorm(0.01)
z

-2.32634787404084

Con una probabilidad del 99% z es igual a 2,32634787404084.

z = qnorm(0.99)
z

2.32634787404084

hist(1,col= "white", border = "white", xlab = "Rendimientos", ylab = "Frecuencia", main = NULL, freq = T, ylim = c(0, 0.4), xlim = c(-5,5))
curve(dnorm(x, mean = 0, sd = 1), add = T, lwd = 3, col = "#3b5998")
abline(v = 0, lwd = 2, lty = 1)
abline(v = qnorm(0.01), lwd = 2, lty = 1)
abline(v = qnorm(0.99), lwd = 2, lty = 1)

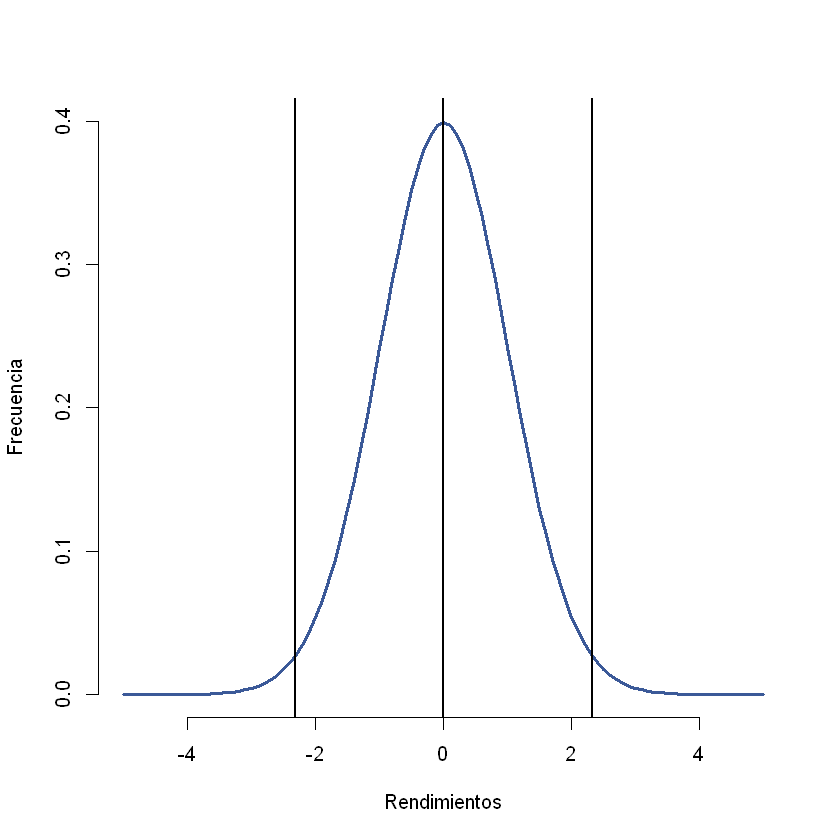
Con una probabilidad del 5% z es igual a -1,64485362695147.

z = qnorm(0.05)
z

-1.64485362695147

Con una probabilidad del 95% z es igual a 1,64485362695147.

z = qnorm(0.95)
z

1.64485362695147

hist(1,col= "white", border = "white", xlab = "Rendimientos", ylab = "Frecuencia", main = NULL, freq = T, ylim = c(0, 0.4), xlim = c(-5,5))
curve(dnorm(x, mean = 0, sd = 1), add = T, lwd = 3, col = "#3b5998")
abline(v = 0, lwd = 2, lty = 1)
abline(v = qnorm(0.05), lwd = 2, lty = 1)
abline(v = qnorm(0.95), lwd = 2, lty = 1)

Ejemplo distribución normal: \(\mu=1\)% y \(\sigma=5\)%

mu = 0.01
volatilidad = 0.05

Con una probabilidad del 1% X es igual a -0,106317393702042.

x = qnorm(0.01, mean = mu, sd = volatilidad)
x

-0.106317393702042

x = mu + qnorm(0.01, sd = volatilidad)
x

-0.106317393702042

Con una probabilidad del 99% X es igual a 0,126317393702042.

x = qnorm(0.99, mean = mu, sd = volatilidad)
x

0.126317393702042

x = mu + qnorm(0.99, sd = volatilidad)
x

0.126317393702042

hist(1,col= "white", border = "white", xlab = "Rendimientos", ylab = "Frecuencia", main = NULL, freq = T, ylim = c(0, 8), xlim = c(-0.3,0.3))
curve(dnorm(x, mean = mu, sd = volatilidad), add = T, lwd = 3, col = "#3b5998")
abline(v = 0, lwd = 2, lty = 1)
abline(v = qnorm(0.01, mean = mu, sd = volatilidad), lwd = 2, lty = 1)
abline(v = qnorm(0.99, mean = mu, sd = volatilidad), lwd = 2, lty = 1)

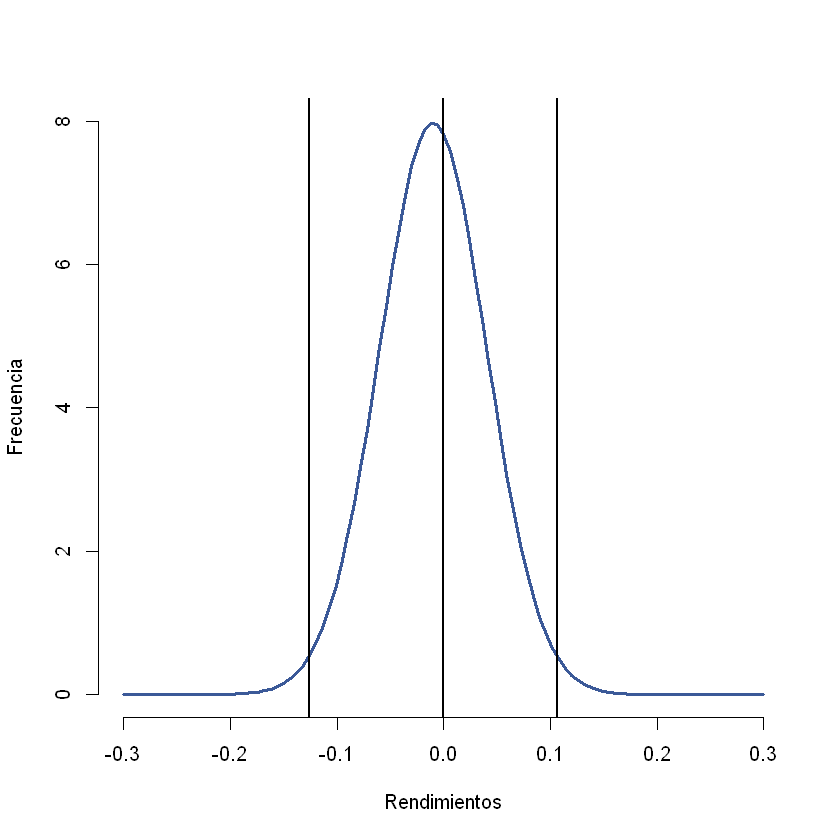
Ejemplo distribución normal: \(\mu=-1\)% y \(\sigma=5\)%

mu = -0.01
volatilidad = 0.05

Con una probabilidad del 1% X es igual a -0,126317393702042.

x = qnorm(0.01, mean = mu, sd = volatilidad)
x

-0.126317393702042

x = mu + qnorm(0.01, sd = volatilidad)
x

-0.126317393702042

Con una probabilidad del 99% X es igual a 0,106317393702042.

x = qnorm(0.99, mean = mu, sd = volatilidad)
x

0.106317393702042

x = mu + qnorm(0.99, sd = volatilidad)
x

0.106317393702042

hist(1,col= "white", border = "white", xlab = "Rendimientos", ylab = "Frecuencia", main = NULL, freq = T, ylim = c(0, 8), xlim = c(-0.3,0.3))
curve(dnorm(x, mean = mu, sd = volatilidad), add = T, lwd = 3, col = "#3b5998")
abline(v = 0, lwd = 2, lty = 1)
abline(v = qnorm(0.01, mean = mu, sd = volatilidad), lwd = 2, lty = 1)
abline(v = qnorm(0.99, mean = mu, sd = volatilidad), lwd = 2, lty = 1)

Importar datos.

datos = read.csv("COLCAP.csv", sep = ";", dec = ",", header = T)

Vector de puntos del COLCAP.

Los índices no son precios, son puntos.

precios = datos[,-1]

precios = ts(precios)

Vector de rendimientos.

rendimientos = diff(log(precios))

\(\mu:\) Rendimiento esperado del índice.

rendimiento_esperado = mean(rendimientos)
rendimiento_esperado

-0.000252769425608668

\(\sigma:\)Volatilidad del índice.

volatilidad = sd(rendimientos)
volatilidad

0.0138522072303189

Gráfico: puntos del COLCAP.

plot(precios, xlab = "Tiempo", ylab = "Puntos", col = "#3b5998", lwd = 3)

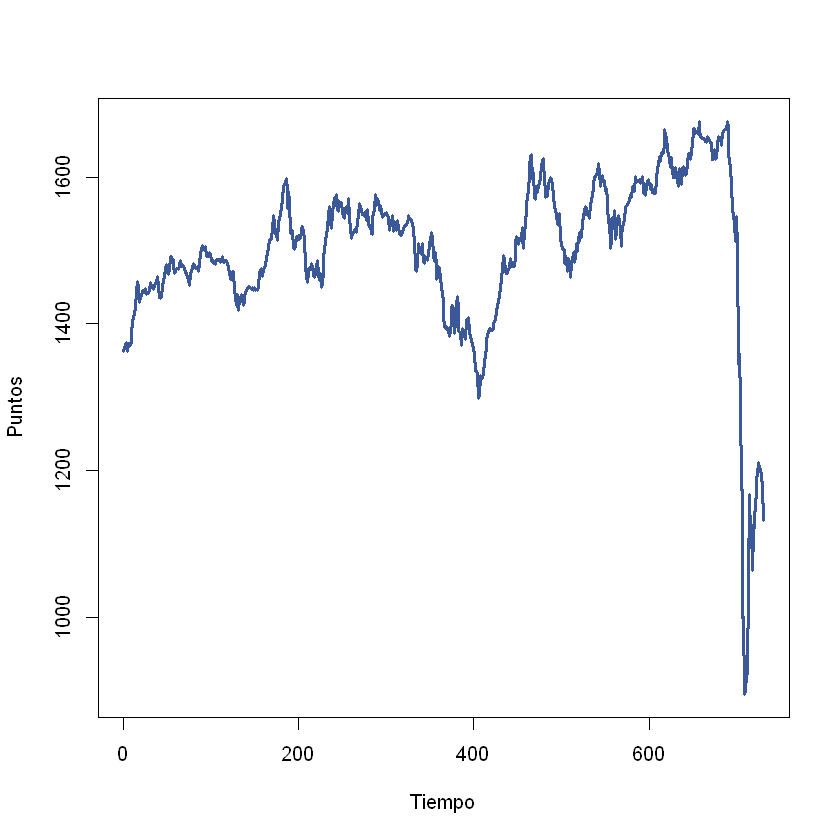
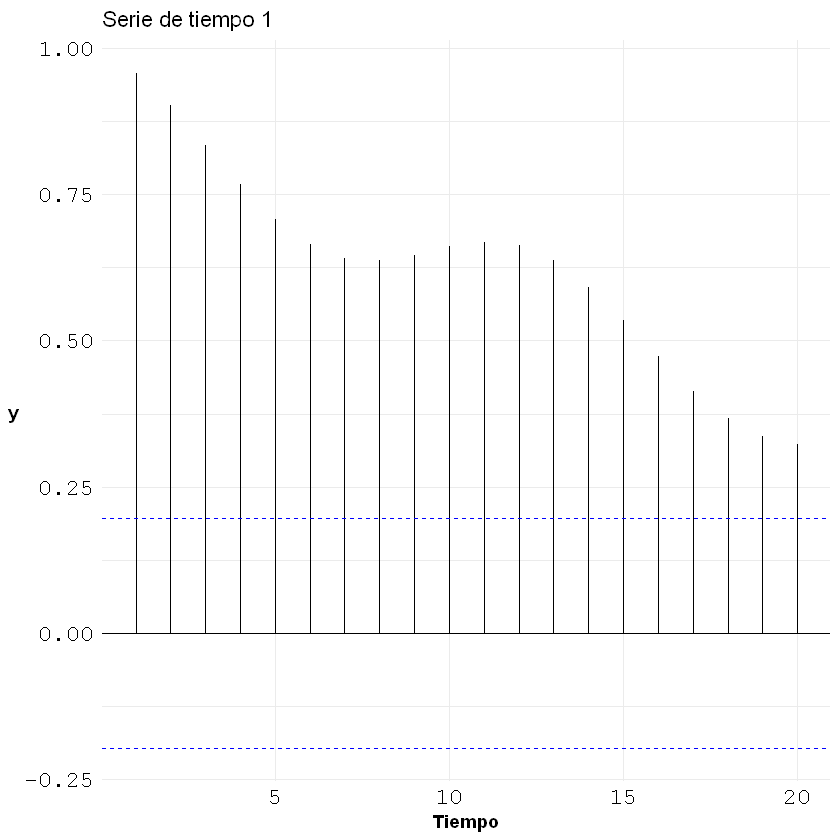
Gráfico: rendimientos.

plot(rendimientos, t = "h", xlab = "Tiempo", ylab = "Rendimientos", col = "#3b5998", lwd = 2)

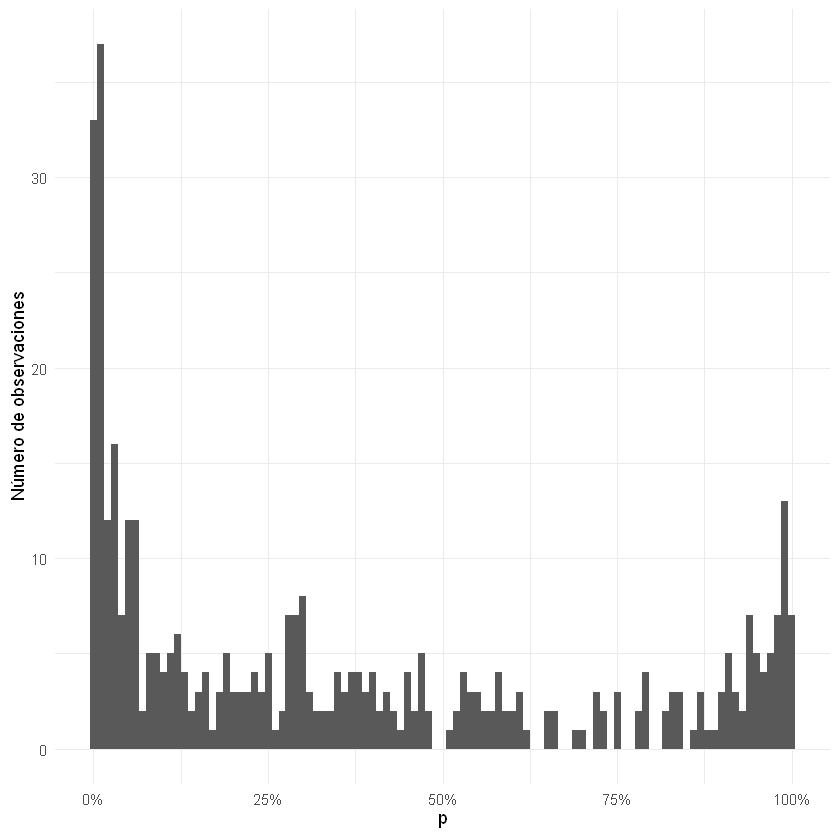
Gráfico: histograma de los rendimientos

hist(rendimientos, breaks = 60, col= "#3b5998", xlab = "Rendimientos", ylab = "Frecuencia", main = "Índice COLCAP", freq = F)

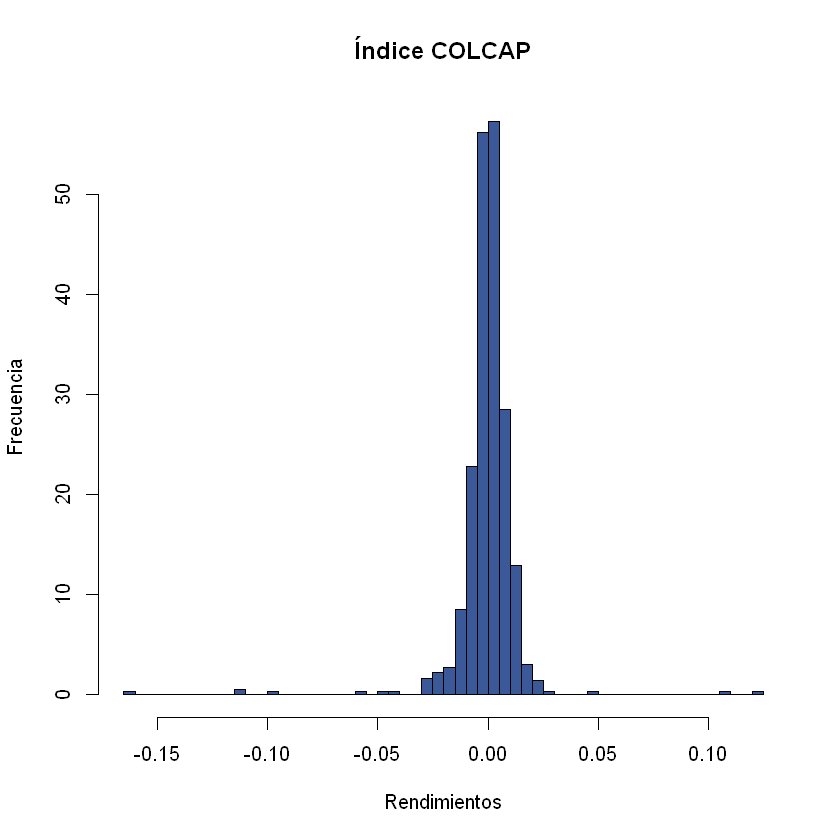
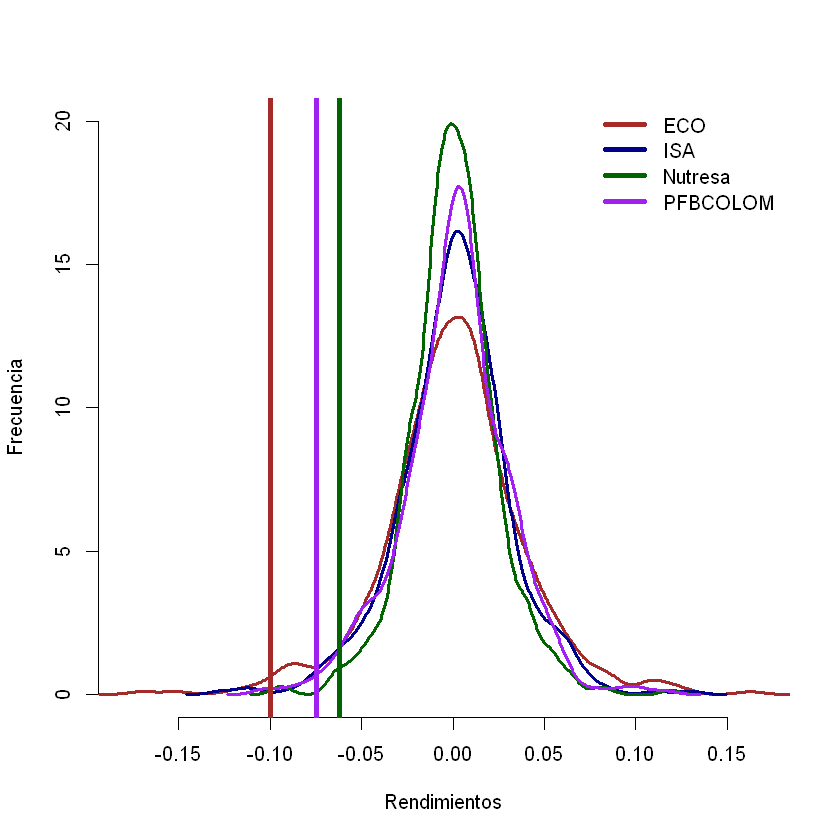
Gráfico: Histograma y distribución normal con \(\mu=0\).

hist(rendimientos, breaks = 60, col= "gray", border = "white", xlab = "Rendimientos", ylab = "Frecuencia", main = "Índice COLCAP", freq = F)
curve(dnorm(x, mean = 0, sd = volatilidad*sqrt(1)), add = T, lwd = 3, col = "#3b5998")

Gráfico: distribución normal con \(\mu=0\).

hist(rendimientos,col= "white", border = "white", xlab = "Rendimientos", ylab = "Frecuencia", main = NULL, freq = F, ylim = c(0, 30))
curve(dnorm(x, mean = 0, sd = volatilidad*sqrt(1)), add = T, lwd = 3, col = "#3b5998")
curve(dnorm(x, mean = 0, sd = volatilidad*sqrt(5)), add = T, lwd = 3, col = "firebrick3")
curve(dnorm(x, mean = 0, sd = volatilidad*sqrt(10)), add = T, lwd = 3, col = "forestgreen")
curve(dnorm(x, mean = 0, sd = volatilidad*sqrt(20)), add = T, lwd = 3)
legend("topright", c("Diaria", "Semanal", "15 días", "Mensual"), col = c("#3b5998", "firebrick3", "forestgreen", "black"), lty = c(1,1,1,1), lwd = 3, bty = "n")

Gráfico: distribución normal con \(\mu=0\) y percentiles.

hist(rendimientos,col= "white", border = "white", xlab = "Rendimientos", ylab = "Frecuencia", main = NULL, freq = F, ylim = c(0, 30))
curve(dnorm(x, mean = 0, sd = volatilidad*sqrt(1)), add = T, lwd = 3, col = "#3b5998")
curve(dnorm(x, mean = 0, sd = volatilidad*sqrt(5)), add = T, lwd = 3, col = "firebrick3")
curve(dnorm(x, mean = 0, sd = volatilidad*sqrt(10)), add = T, lwd = 3, col = "forestgreen")
curve(dnorm(x, mean = 0, sd = volatilidad*sqrt(20)), add = T, lwd = 3)
abline(v = -volatilidad*qnorm(0.99)*sqrt(1), lwd = 3, col = "#3b5998")
abline(v = -volatilidad*qnorm(0.99)*sqrt(5), lwd = 3, col = "firebrick3")
abline(v = -volatilidad*qnorm(0.99)*sqrt(10), lwd = 3, col = "forestgreen")
abline(v = -volatilidad*qnorm(0.99)*sqrt(20), lwd = 3)
legend("topright", c("Diaria", "Semanal", "15 días", "Mensual"), col = c("#3b5998", "firebrick3", "forestgreen", "black"), lty = c(1,1,1,1), lwd = 3, bty = "n")

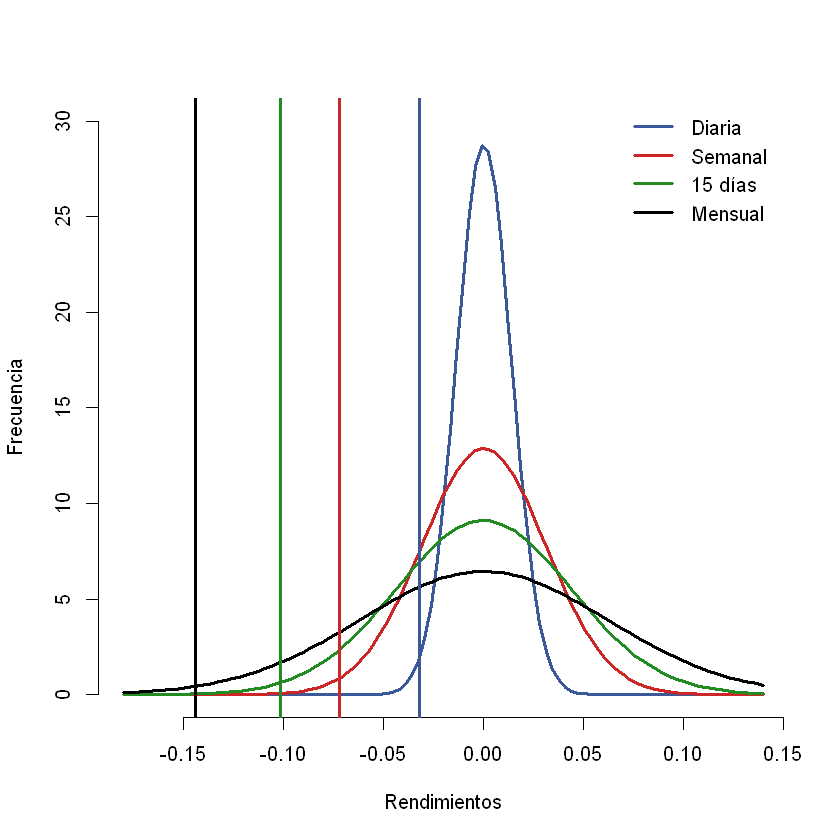
Gráfico: distribución normal con \(\mu\neq0\).

hist(rendimientos,col= "white", border = "white", xlab = "Rendimientos", ylab = "Frecuencia", main = NULL, freq = F, ylim = c(0, 30))
curve(dnorm(x, mean = rendimiento_esperado*1, sd = volatilidad*sqrt(1)), add = T, lwd = 3, col = "#3b5998")
curve(dnorm(x, mean = rendimiento_esperado*5, sd = volatilidad*sqrt(5)), add = T, lwd = 3, col = "firebrick3")
curve(dnorm(x, mean = rendimiento_esperado*10, sd = volatilidad*sqrt(10)), add = T, lwd = 3, col = "forestgreen")
curve(dnorm(x, mean = rendimiento_esperado*20, sd = volatilidad*sqrt(20)), add = T, lwd = 3)
abline(v = rendimiento_esperado*20, lwd = 3, lty = 1)
legend("topright", c("Diaria", "Semanal", "15 días", "Mensual"), col = c("#3b5998", "firebrick3", "forestgreen", "black"), lty = c(1,1,1,1), lwd = 3, bty = "n")