Repaso Álgebra Lineal#
Determinantes:#
Matrices \(2x2\):
El área del plano se llama Determinante.
El área es igual a \(4\times4=16\). Para matrices de orden 2 \((2x2)\) el Determinante se calcula multiplicando los valores de la diagonal principal y restando la multiplicación de la diagonal secundaria.
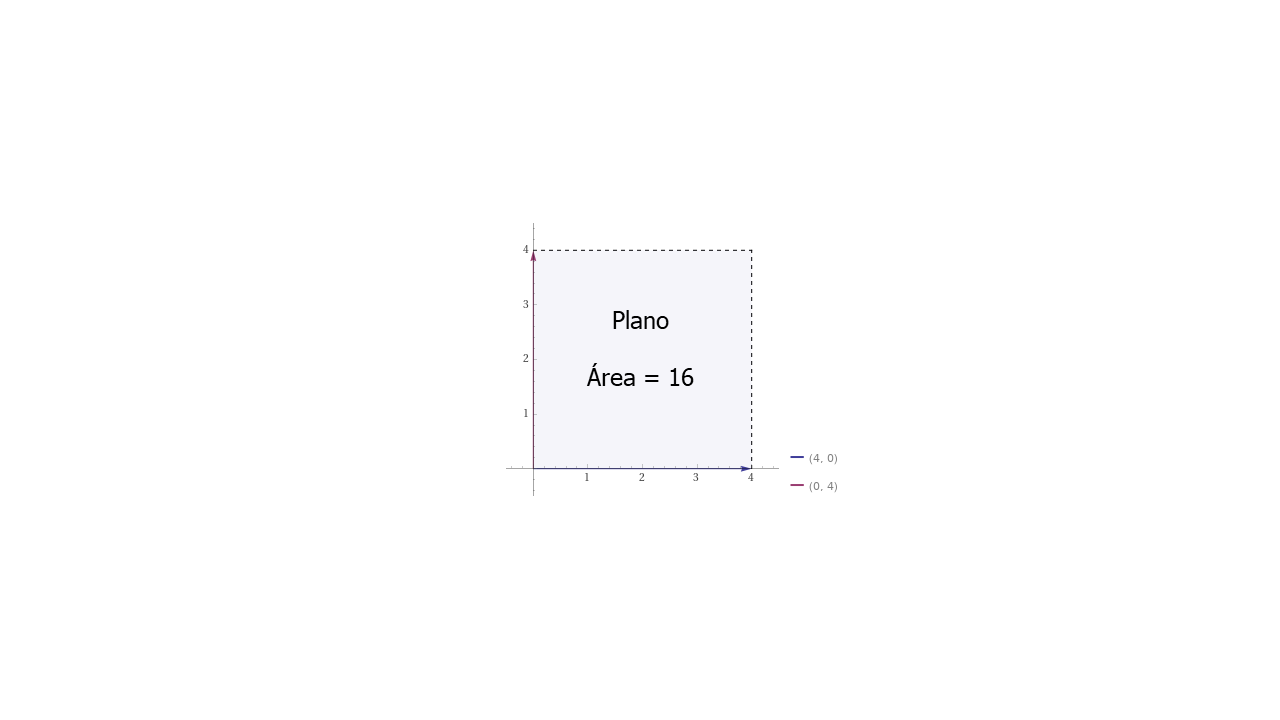
Plano#
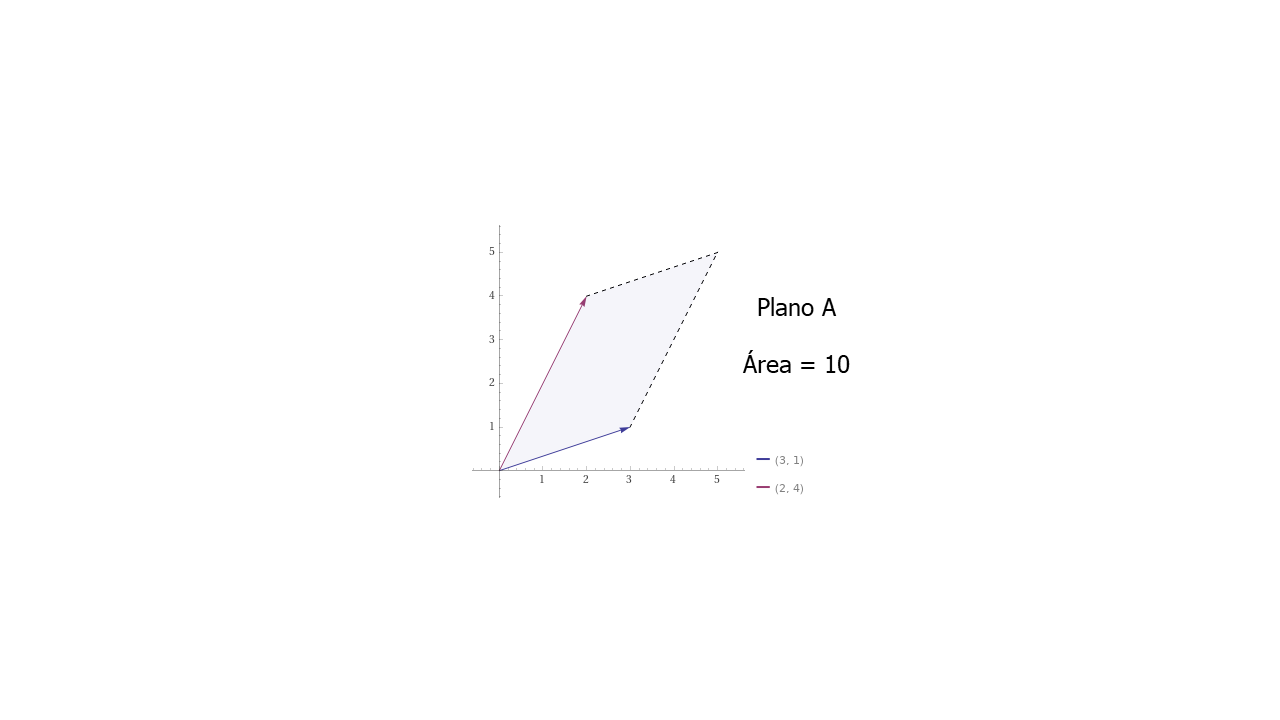
PlanoA#
Siendo \(A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\)
En ocasiones vemos que el Determinante se expresa en valor absoluto así \(det(A) = |A|\), pero también se puede expresar con el signo negativo. Esto ocurre si cambiamos el orden de los vectores.
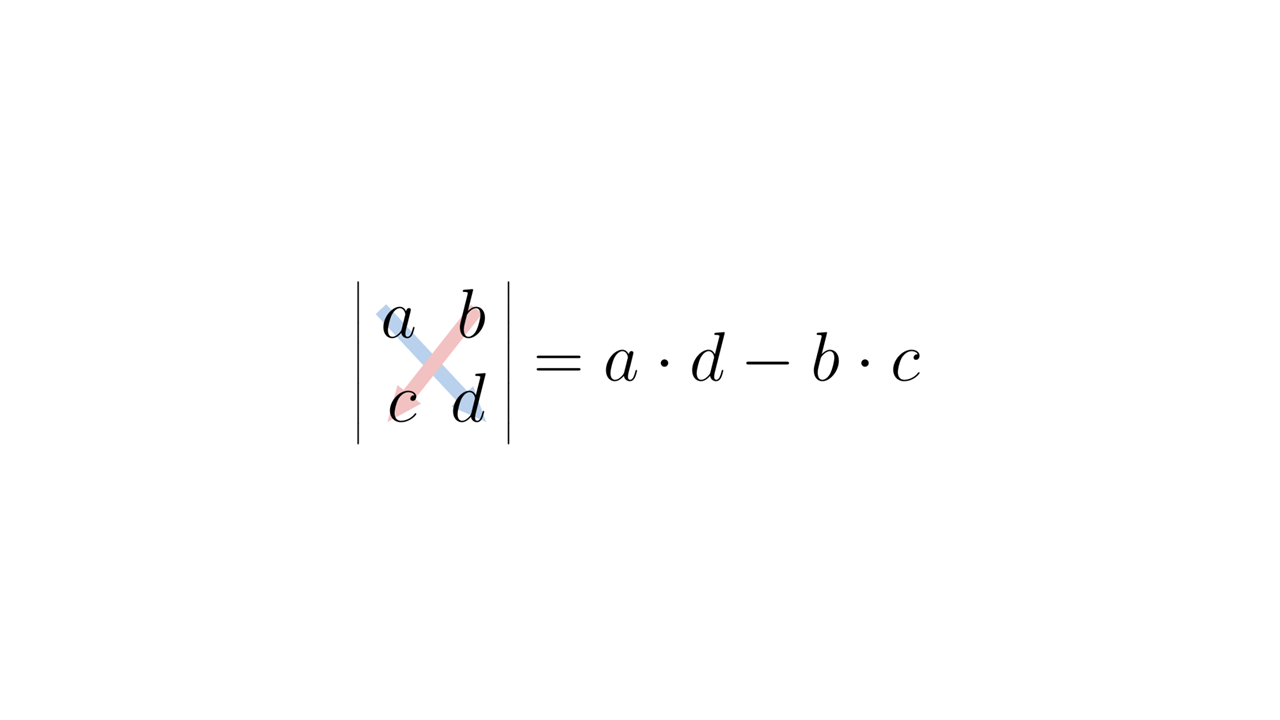
Determinante2x2#
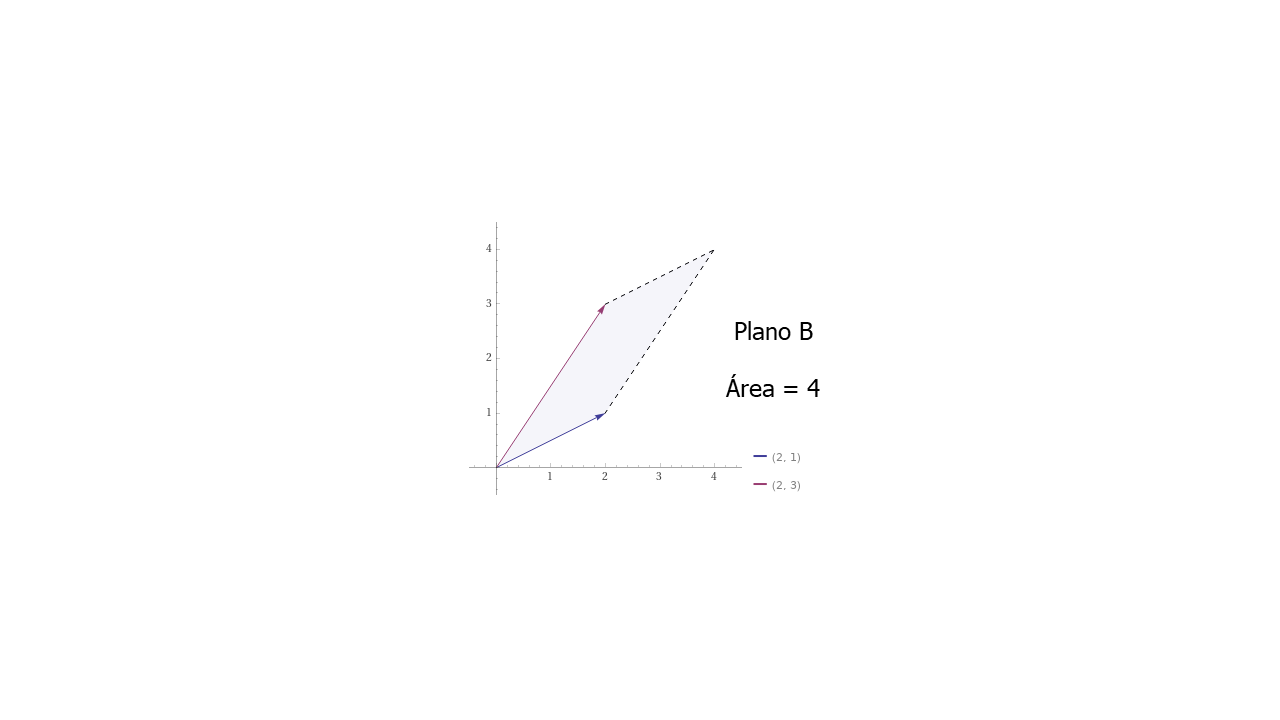
PlanoB#
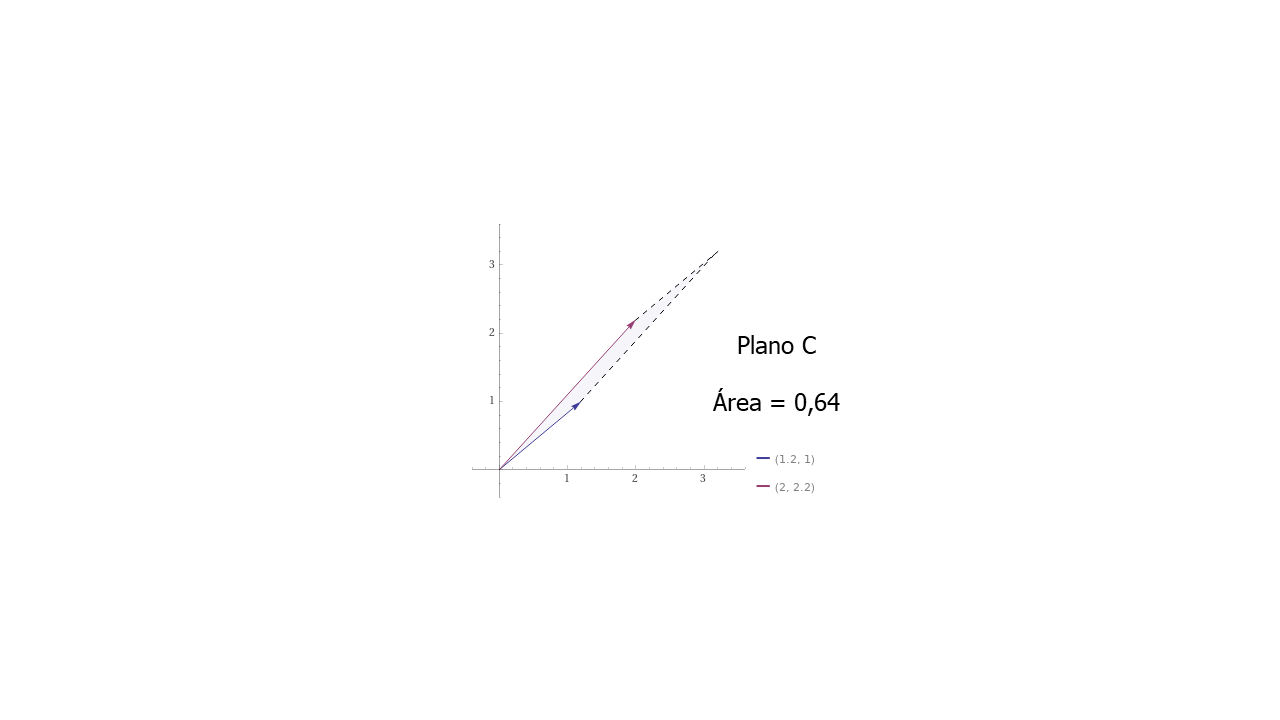
PlanoC#
Note que en los ejemplos de las matrices \(A\), \(B\) y \(C\) los valores de la diagonal principal disminuyen y se obtiene un Determinante menor. Es fácil intuir que un Determinante más pequeño, por ejemplo, igual a cero, el resultado es un solo vector. Este vector, más adelante se llamará Autovector.
Matrices \(3x3\):
Para matrices \(3\times3\) el Determinante (volumen, no área) es:
Siendo \(A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i\end{bmatrix}\)
Transformaciones lineales:#
Una matriz podría verse como una transformación lineal porque transforman linealmente los vectores unitarios (\(\hat{i}\), \(\hat{j}\)).
Los vectores unitarios conforman el siguiente plano:
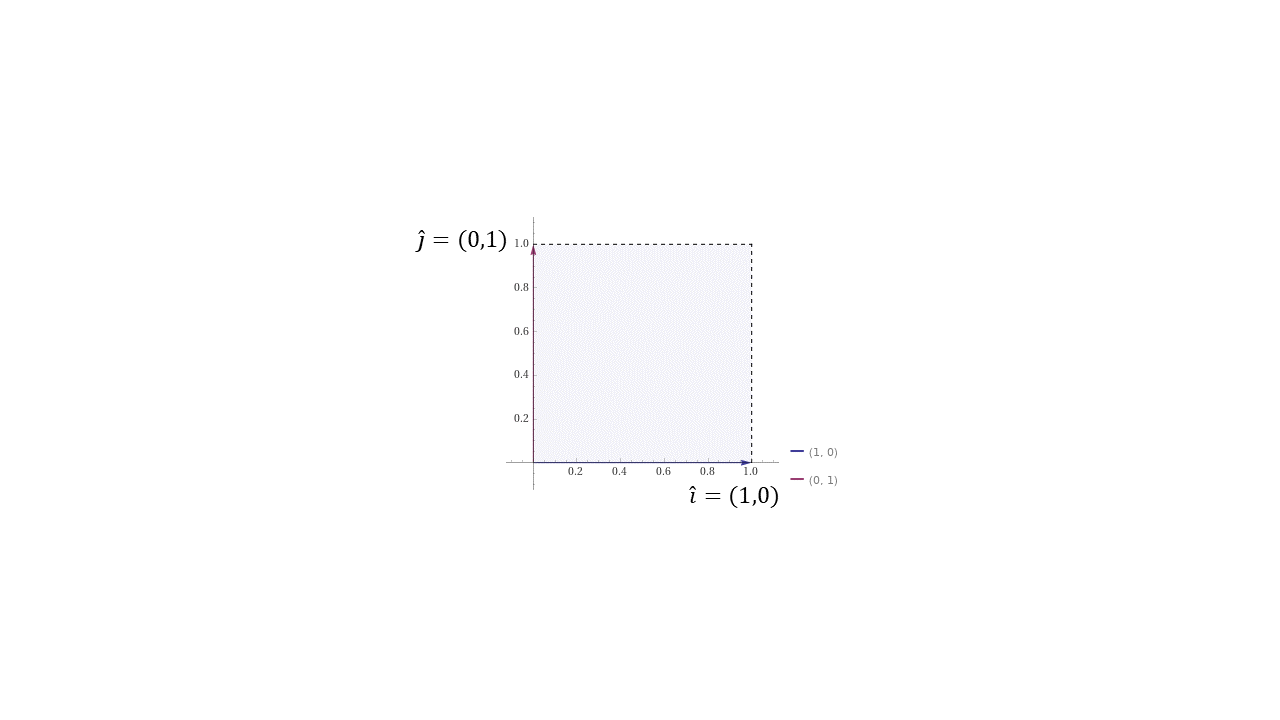
VectoresUnitarios#
Siendo \(A =\begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix}\), la transformación lineal de los dos vectores unitarios es la siguiente:
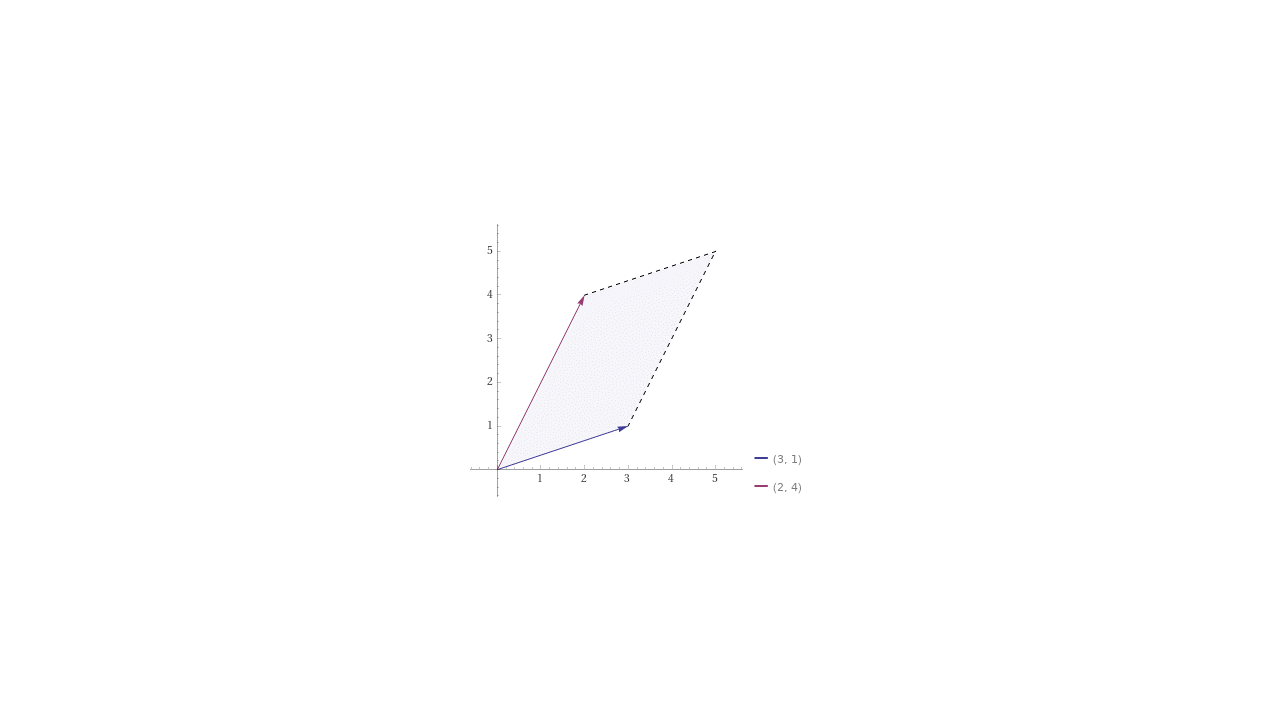
TransformaciónLineal#
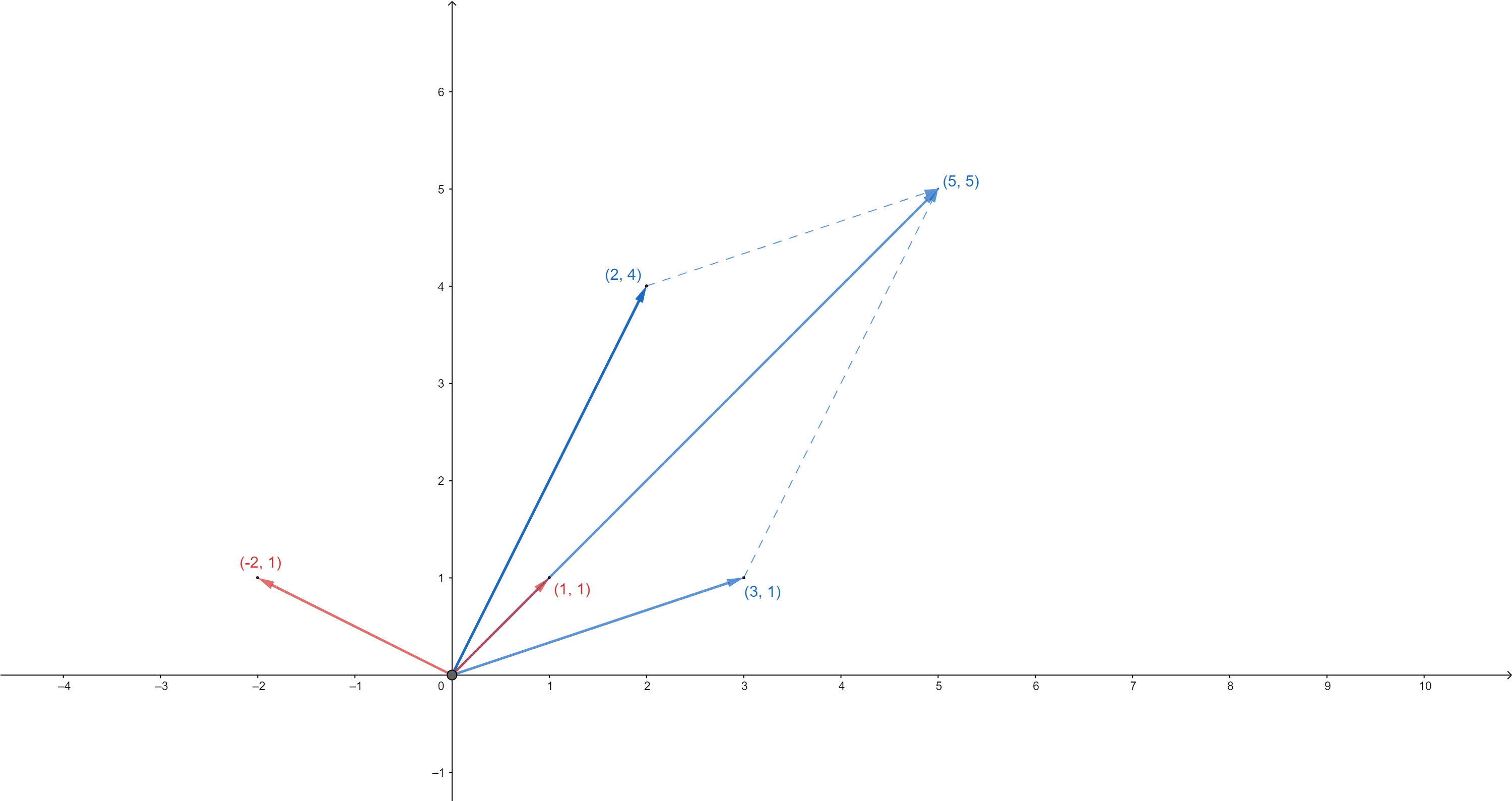
Analicemos la transformación que realizó la matriz \(A\) a tres vectores del plano de vectores unitarios:
El vector \(\begin{bmatrix} 1 \\ 0 \end{bmatrix}\) se transformó en el vector \(\begin{bmatrix} 3 \\ 1 \end{bmatrix}\). El vector nuevo tiene una dirección diferente que el inicial.
El vector \(\begin{bmatrix} 0 \\ 1 \end{bmatrix}\) se transformó en el vector \(\begin{bmatrix} 2 \\ 4 \end{bmatrix}\). El vector nuevo tiene una dirección diferente que el inicial.
El vector \(\begin{bmatrix} 1 \\ 1 \end{bmatrix}\) se transformó en el vector \(\begin{bmatrix} 5 \\ 5 \end{bmatrix}\). El vector nuevo sí conservó la dirección, pero tiene una magnitud diferente (es un vector escalado).
Al hacer la transformación lineal de \(A\), el vector transformado \(\begin{bmatrix} 5 \\ 5 \end{bmatrix}\) es el mismo vector \(\begin{bmatrix} 1 \\ 1 \end{bmatrix}\), pero con una magnitud de 5, es decir: \(\begin{bmatrix} 5 \\ 5 \end{bmatrix} = 5\begin{bmatrix} 1 \\ 1 \end{bmatrix}\). Así que el vector \(\begin{bmatrix} 1 \\ 1 \end{bmatrix}\) se llama Autovector o Eigenvector de la matriz \(A\) y el escalar 5 se llama Autovalor o Eigenvalor de la matriz \(A\).
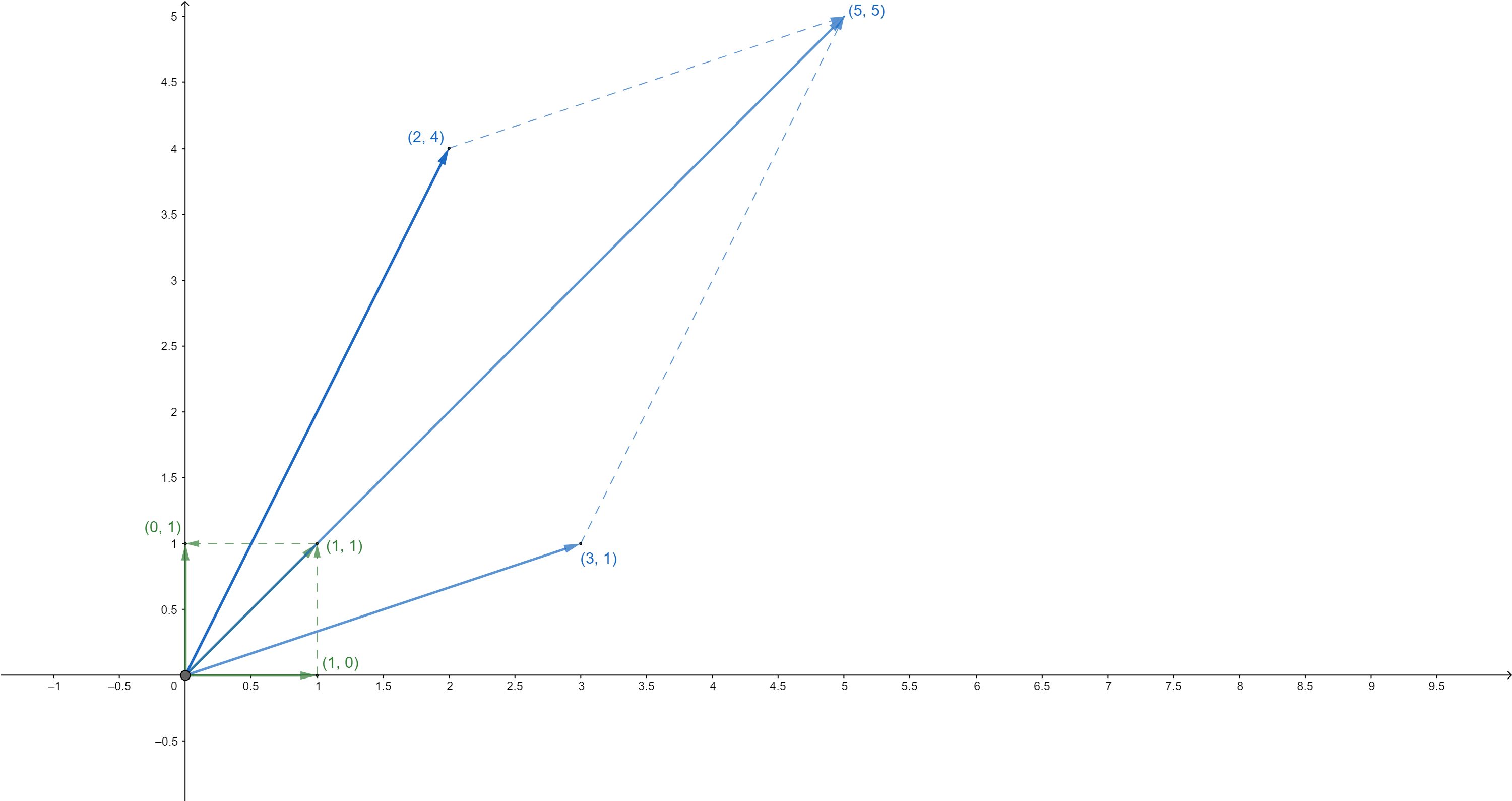
TransformaciónLineal.#
Autovalores y Autovectores:#
Con lo anterior podemos concluir que un Autovector \((x)\) es aquel que es transformado por una matriz y conserva su dirección, pero puede aumentar o disminuir de magnitud en \(\lambda\) veces. Por tanto, el escalar \(\lambda\) es un Autovalor. Lo anterior cumple la siguiente ecuación:
Donde,
\(A\): es una matriz del orden \(nxn\).
\(x\): es el Autovector o Eigenvector de \(A\).
\(\lambda\): es el Autovalor o Eigenvalor de \(A\). Es un escalar.
Para el ejemplo:
Para hallar \(x\) y \(\lambda\) matemáticamente se hace lo siguiente:
\(I\): es la matriz identidad.
\(det(A - \lambda I)=0\) es llamada ecuación característica.
Anteriormente, gráficamente habíamos restado solo los valores de la diagonal principal de la matriz \(A = \begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix}\), se había concluido que el Determinante se volvía cero y el vector resultante era \(\begin{bmatrix} 1 \\ 1 \end{bmatrix}\). Este vector es el Autovector de la matriz \(A\).
Entonces, \(\lambda\) es Autovalor de \(A\) si y solo si: \(det(A - \lambda I)) = 0\)
Para una matriz del orden \(nxn\) tendremos \(n\) Autovectores y \(n\) Autovalores. En el ejemplo anterior se mencionó un Autovector y un Autovalor, pero la solución completa es la siguiente:
Para estos dos Autovalores, los dos Autovectores son:
Para \(\lambda_1 = 2\), \(x_1=\begin{bmatrix} -2 \\ 1 \end{bmatrix}\)
Para \(\lambda_2 = 5\), \(x_2=\begin{bmatrix} 1 \\ 1 \end{bmatrix}\)
Los dos Autovectores son ortogonales, tienen un ángulo de 90°.
Autovectores#