SVR series de tiempo con lags#
import numpy as np
import pandas as pd
from sklearn.svm import SVR
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import scipy.stats as stats
from sklearn.model_selection import RandomizedSearchCV
import warnings
# Suprimir todas las advertencias
warnings.filterwarnings("ignore")
# Cargar los datos omitiendo la primera fila como encabezado y asignando nombres a las columnas
data = pd.read_csv("../Irradiance_mensual.csv", skiprows=1, header=None, names=["Fecha", "Irradiancia"])
# Convertir la columna 'Fecha' a datetime
data["Fecha"] = pd.to_datetime(data["Fecha"], format="%Y-%m")
# Set 'Fecha' as the index
data.set_index("Fecha", inplace=True)
# Cantidad de datos
n = data.shape[0]
print("Cantidad de datos:", n)
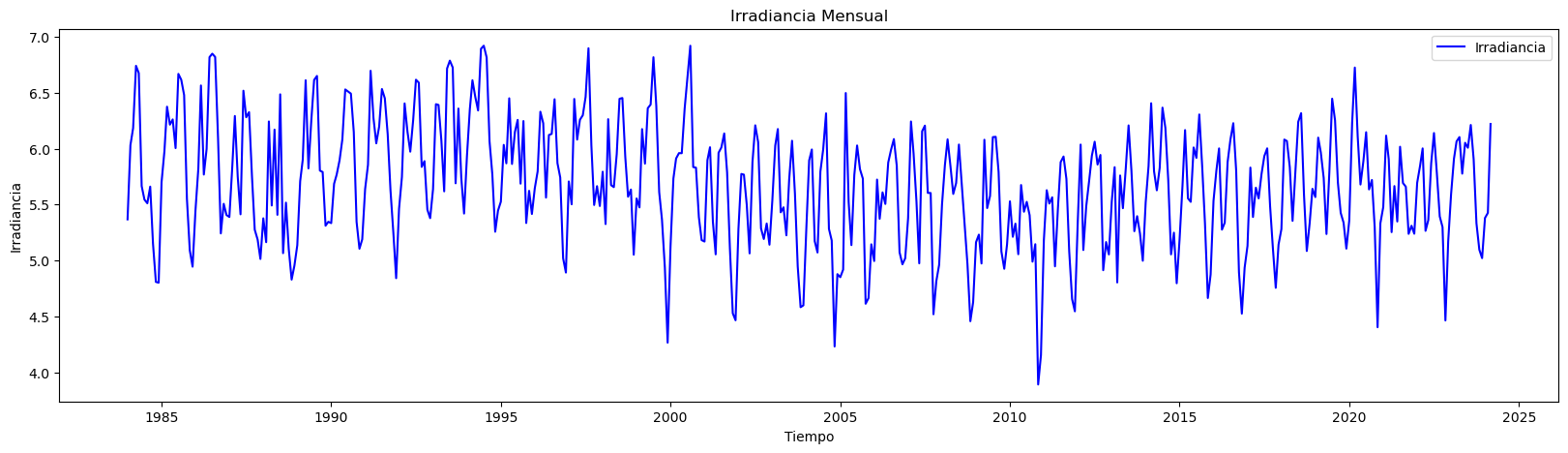
plt.figure(figsize=(20, 5)) # Establecer el tamaño del gráfico
plt.plot(data.index, data["Irradiancia"], label="Irradiancia", color="blue") # Dibujar los datos reales
plt.title("Irradiancia Mensual") # Título del gráfico
plt.xlabel("Tiempo") # Etiqueta del eje X
plt.ylabel("Irradiancia") # Etiqueta del eje Y
plt.legend() # Añadir leyenda para identificar las líneas
plt.show()
Cantidad de datos: 483
Lags de la serie de tiempo como variables de entrada:#
# Crear características de lags
n_lags = 12 # Número de lags que deseas utilizar
data_lags = data.copy()
for lag in range(1, n_lags + 1):
data_lags[f"Irradiancia_Lag_{lag}"] = data["Irradiancia"].shift(lag)
# Eliminar las filas con valores NaN resultantes de los lags
data_lags.dropna(inplace=True)
print(data_lags.head())
Irradiancia Irradiancia_Lag_1 Irradiancia_Lag_2 Fecha
1985-01-01 5.699355 4.802258 4.808667
1985-02-01 5.977500 5.699355 4.802258
1985-03-01 6.374194 5.977500 5.699355
1985-04-01 6.214000 6.374194 5.977500
1985-05-01 6.260645 6.214000 6.374194
Irradiancia_Lag_3 Irradiancia_Lag_4 Irradiancia_Lag_5 Fecha
1985-01-01 5.150323 5.660333 5.511290
1985-02-01 4.808667 5.150323 5.660333
1985-03-01 4.802258 4.808667 5.150323
1985-04-01 5.699355 4.802258 4.808667
1985-05-01 5.977500 5.699355 4.802258
Irradiancia_Lag_6 Irradiancia_Lag_7 Irradiancia_Lag_8 Fecha
1985-01-01 5.544516 5.665000 6.674194
1985-02-01 5.511290 5.544516 5.665000
1985-03-01 5.660333 5.511290 5.544516
1985-04-01 5.150323 5.660333 5.511290
1985-05-01 4.808667 5.150323 5.660333
Irradiancia_Lag_9 Irradiancia_Lag_10 Irradiancia_Lag_11 Fecha
1985-01-01 6.739667 6.182903 6.030690
1985-02-01 6.674194 6.739667 6.182903
1985-03-01 5.665000 6.674194 6.739667
1985-04-01 5.544516 5.665000 6.674194
1985-05-01 5.511290 5.544516 5.665000
Irradiancia_Lag_12
Fecha
1985-01-01 5.367742
1985-02-01 6.030690
1985-03-01 6.182903
1985-04-01 6.739667
1985-05-01 6.674194
# Separar características (X) y la variable objetivo (y)
X = data_lags.drop(columns=["Irradiancia"])
y = data_lags["Irradiancia"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=False, random_state=34)
# Crear escaladores para X e y
scaler_X = StandardScaler()
scaler_y = StandardScaler()
# Ajustar y transformar X_train, luego transformar X_test con el mismo escalador
X_train_scaled = scaler_X.fit_transform(X_train)
X_test_scaled = scaler_X.transform(X_test)
# Ajustar y transformar y_train, luego transformar y_test con el mismo escalador
y_train_scaled = scaler_y.fit_transform(y_train.values.reshape(-1, 1)).flatten()
y_test_scaled = scaler_y.transform(y_test.values.reshape(-1, 1)).flatten()
Optimización de Hiperparámetros:#
Los hiperparámetros como C, epsilon, y gamma pueden variar
en órdenes de magnitud, es decir, desde valores muy pequeños (por
ejemplo, 0.001) hasta valores muy grandes (por ejemplo, 1000). Usar un
rango logarítmico permite explorar de manera más efectiva valores
pequeños y grandes, capturando la sensibilidad del modelo a estos
parámetros.
np.logspace(-3, 3, 10)
array([1.00000000e-03, 4.64158883e-03, 2.15443469e-02, 1.00000000e-01,
4.64158883e-01, 2.15443469e+00, 1.00000000e+01, 4.64158883e+01,
2.15443469e+02, 1.00000000e+03])
# Definir el modelo SVR
svr = SVR()
# Definir el espacio de búsqueda de hiperparámetros
param_dist = {
"C": np.logspace(-3, 3, 10), # Valor de C en un rango logarítmico
"epsilon": np.logspace(-4, 1, 10), # Epsilon en un rango logarítmico
"kernel": ["linear", "rbf", "poly", "sigmoid"], # Diferentes kernels
"gamma": ["scale", "auto"] + list(np.logspace(-4, 1, 10)), # Gamma con opciones y un rango logarítmico
"degree": [2, 3, 4, 5], # Grados para el kernel polinomial
"coef0": [0.0, 0.1, 0.5, 1.0], # Coeficiente 0 para kernels polinomial y sigmoide
}
# Configurar RandomizedSearchCV
random_search = RandomizedSearchCV(
estimator=svr,
param_distributions=param_dist,
n_iter=30, # Número de combinaciones aleatorias a evaluar
scoring="neg_mean_squared_error", # Métrica de evaluación
cv=5, # Número de divisiones para la validación cruzada
verbose=2,
random_state=34,
n_jobs=-1, # Utilizar todos los núcleos disponibles
)
# Ajustar RandomizedSearchCV al conjunto de entrenamiento
random_search.fit(X_train_scaled, y_train_scaled)
Fitting 5 folds for each of 30 candidates, totalling 150 fits
RandomizedSearchCV(cv=5, estimator=SVR(), n_iter=30, n_jobs=-1,
param_distributions={'C': array([1.00000000e-03, 4.64158883e-03, 2.15443469e-02, 1.00000000e-01,
4.64158883e-01, 2.15443469e+00, 1.00000000e+01, 4.64158883e+01,
2.15443469e+02, 1.00000000e+03]),
'coef0': [0.0, 0.1, 0.5, 1.0],
'degree': [2, 3, 4, 5],
'epsilon': array([1.00000000e-04, 3.59381366e-04, 1.29154967e-03...
1.66810054e-02, 5.99484250e-02, 2.15443469e-01, 7.74263683e-01,
2.78255940e+00, 1.00000000e+01]),
'gamma': ['scale', 'auto', 0.0001,
0.00035938136638046257,
0.001291549665014884,
0.004641588833612782,
0.016681005372000592,
0.05994842503189409,
0.21544346900318845,
0.7742636826811278,
2.782559402207126, 10.0],
'kernel': ['linear', 'rbf', 'poly',
'sigmoid']},
random_state=34, scoring='neg_mean_squared_error',
verbose=2)
Si pones n_iter=40 ¿cuánto se demora en ejecutarse?
# Obtener los mejores hiperparámetros
best_params = random_search.best_params_
best_score = random_search.best_score_
print(f"Mejores hiperparámetros: {best_params}")
print(f"Mejor MSE: {best_score}")
Mejores hiperparámetros: {'kernel': 'rbf', 'gamma': 0.0001, 'epsilon': 0.05994842503189409, 'degree': 3, 'coef0': 0.1, 'C': 215.44346900318823}
Mejor MSE: -0.4132827538647449
# Usar el mejor modelo encontrado para hacer predicciones
best_model = random_search.best_estimator_
Análisis de los residuales:#
# Calcular los residuales sobre train
y_pred_train_scaled = random_search.predict(X_train_scaled)
y_pred_train = scaler_y.inverse_transform(y_pred_train_scaled.reshape(-1, 1))
residuals_train = y_train.values - y_pred_train.flatten()
# Hacer predicciones en el conjunto de entrenamiento
y_pred_train = best_model.predict(X_train_scaled)
# Desescalar las predicciones para obtener los valores originales
y_pred_train_descaled = scaler_y.inverse_transform(
y_pred_train.reshape(-1, 1)
).flatten()
# Calcular los residuales sobre el conjunto de entrenamiento
residuals_train = y_train.values - y_pred_train_descaled
# Configuración de la figura para los subplots
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(14, 6))
# Gráfico de valores predichos vs. valores reales
axs[0].scatter(y_pred_train_descaled, y_train.values, color="blue", alpha=0.5)
axs[0].plot(
[y_train.min(), y_train.max()], [y_train.min(), y_train.max()], "k--", lw=2
) # Línea diagonal ideal
axs[0].set_title("Valores Reales vs. Valores Predichos (Train)")
axs[0].set_xlabel("Valores Predichos")
axs[0].set_ylabel("Valores Reales")
# Gráfico de residuales
axs[1].scatter(y_train.index, residuals_train, color="purple", alpha=0.3)
axs[1].axhline(y=0, color="black", linestyle="--") # Línea en y=0 para referencia
axs[1].set_title("Gráfico de Residuales (Train)")
axs[1].set_xlabel("Fecha")
axs[1].set_ylabel("Residuales")
# Mejorar el layout para evitar solapamientos
plt.tight_layout()
# Mostrar la figura
plt.show()
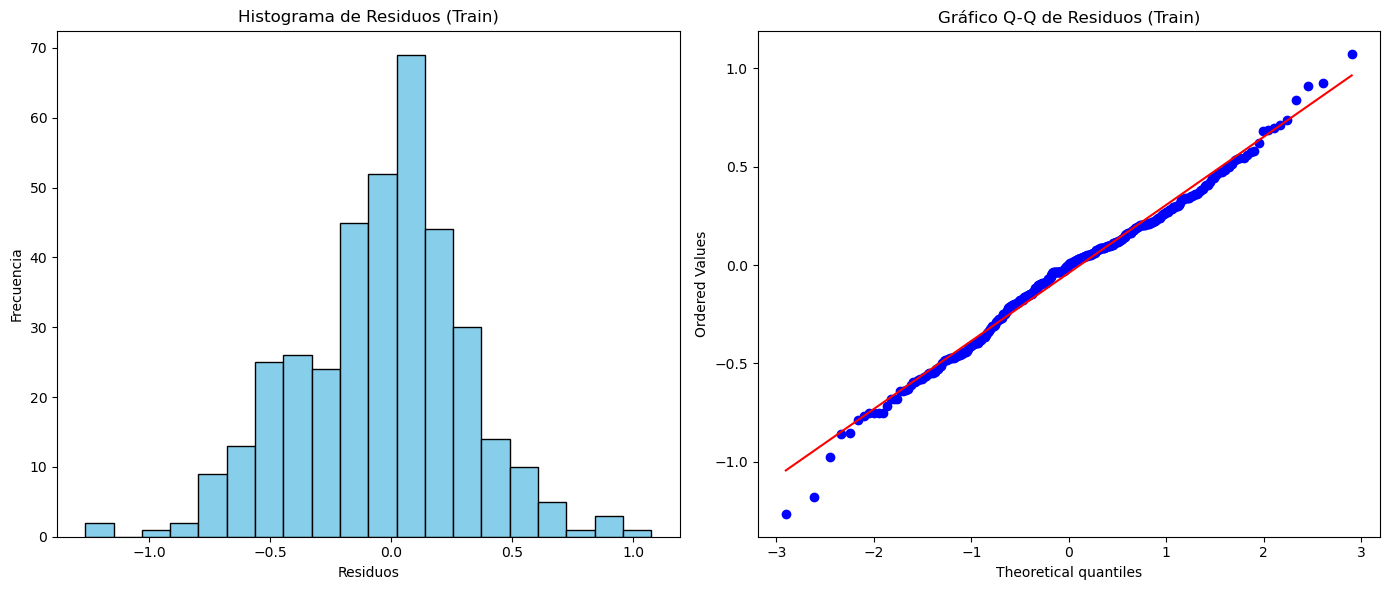
# Visualización del histograma de los residuos
plt.figure(figsize=(14, 6))
plt.subplot(1, 2, 1)
plt.hist(residuals_train, bins=20, color="skyblue", edgecolor="black")
plt.title("Histograma de Residuos (Train)")
plt.xlabel("Residuos")
plt.ylabel("Frecuencia")
# Visualización del gráfico Q-Q de los residuos
plt.subplot(1, 2, 2)
stats.probplot(residuals_train, dist="norm", plot=plt)
plt.title("Gráfico Q-Q de Residuos (Train)")
# Ajustar el diseño de la figura
plt.tight_layout()
# Mostrar la figura
plt.show()
Predicciones fuera de la muestra:#
# Preparar el punto de partida (última fila de X_test)
last_X = X_test.iloc[-1].values.reshape(1, -1)
# Número de pasos adelante para predecir
n_steps_ahead = 12 * 5
# Lista para almacenar las predicciones fuera de muestra
predictions_out_of_sample = []
for _ in range(n_steps_ahead):
# Hacer la predicción usando el último valor de X
pred = best_model.predict(last_X)
# Guardar la predicción
predictions_out_of_sample.append(pred[0])
# Crear la nueva entrada para la siguiente predicción utilizando los lags
new_X = np.roll(last_X, shift=-1) # Desplazar valores
new_X[0, -n_lags:] = pred # Actualizar con la nueva predicción
last_X = new_X.reshape(1, -1) # Reajustar la forma
# Crear un rango de fechas para las predicciones fuera de muestra
dates_out_of_sample = pd.date_range(
start=y_test.index[-1], periods=n_steps_ahead + 1, freq="M"
)[1:]
# Graficar las predicciones fuera de muestra
plt.figure(figsize=(10, 6))
plt.plot(y_test.index, y_test, label="Datos Reales (Test)")
plt.plot(
dates_out_of_sample,
predictions_out_of_sample,
label="Predicciones Fuera de Muestra",
color="red",
linestyle="--",
)
plt.title("Predicciones fuera de la muestra con SVR (con Lags)")
plt.xlabel("Fecha")
plt.ylabel("Valores Predichos")
plt.legend()
plt.show()