Ejemplo K-Means acciones

import yfinance as yf
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

Descargar precios de acciones con diferentes características.

acciones = [
    # 🟢 Acciones de bajo Beta (< 0.8) — defensivas
    'JNJ',   # Johnson & Johnson
    'PG',    # Procter & Gamble
    'KO',    # Coca-Cola
    'PEP',   # PepsiCo
    'WMT',   # Walmart

    # 🟡 Acciones de Beta cercano a 1 (≈ 0.9 - 1.1) — mercado promedio
    'AAPL',  # Apple
    'MSFT',  # Microsoft
    'V',     # Visa
    'MA',    # Mastercard
    'UNH',   # UnitedHealth

    # 🔴 Acciones de Beta alto (> 1.2) — más volátiles que el mercado
    'TSLA',  # Tesla
    'NVDA',  # Nvidia
    'META',  # Meta (Facebook)
    'AMZN',  # Amazon
    'NFLX',  # Netflix

    # 🔁 Adicionales mixtas para aumentar diversidad
    'GOOGL', # Alphabet (Google)
    'AMD',   # Advanced Micro Devices
    'CRM',   # Salesforce
    'BA',    # Boeing
    'NKE'    # Nike
]

indice = '^GSPC'  # S&P500

datos = yf.download(acciones + [indice], start='2020-07-01', end='2025-07-31', interval='1mo')['Close']
datos.dropna(inplace=True)

datos.describe()

/tmp/ipython-input-4028798923.py:33: FutureWarning:

YF.download() has changed argument auto_adjust default to True

[*******************100%*********************]  21 of 21 completed

Ticker	AAPL	AMD	AMZN	BA	CRM	GOOGL	JNJ	KO	MA	META	...	NFLX	NKE	NVDA	PEP	PG	TSLA	UNH	V	WMT	^GSPC
count	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000	...	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000
mean	168.308617	111.604426	157.696810	192.557214	234.247292	130.157316	148.377781	56.029760	398.977756	351.281432	...	555.438689	106.060138	53.068235	147.862061	141.179574	246.167060	444.539693	241.869441	56.422427	4591.564901
std	37.929745	32.599924	35.406763	31.330118	48.640246	32.428266	9.933564	8.197990	82.631459	165.833286	...	256.862147	26.134750	47.606693	17.024615	16.928581	67.619500	87.096899	50.515682	18.549608	813.091153
min	103.174950	60.060001	84.000000	121.080002	131.438263	72.843147	118.884293	40.592743	279.303253	92.651711	...	174.869995	55.738003	10.579878	111.810875	110.428253	95.384003	249.559998	173.635712	38.834503	3269.959961
25%	138.524826	85.519997	133.089996	171.820007	201.018555	103.111610	142.965118	50.373852	346.991180	252.285919	...	394.519989	88.180077	16.206354	132.809311	127.865395	201.880005	386.012939	206.614441	44.324265	4076.600098
50%	167.575745	102.900002	160.309998	194.190002	236.031754	131.928787	150.120636	56.363876	364.622589	316.861694	...	517.570007	104.602783	27.729069	152.459503	140.274231	240.080002	472.730499	225.510986	47.488297	4395.259766
75%	191.829468	137.179993	176.759995	212.009995	267.514771	154.275345	154.298798	59.936264	447.335114	473.209686	...	641.619995	124.794441	90.315811	159.898743	155.858002	282.160004	498.170746	269.519714	59.013657	5254.350098
max	249.534180	192.529999	237.679993	260.660004	340.623810	203.538895	163.539612	72.037811	584.808716	773.440002	...	1339.130005	159.513474	177.869995	175.766800	175.867126	404.600006	601.015320	363.944122	98.252411	6339.390137

8 rows × 21 columns

datos.info()

<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 61 entries, 2020-07-01 to 2025-07-01
Data columns (total 21 columns):
 #   Column  Non-Null Count  Dtype
---  ------  --------------  -----
 0   AAPL    61 non-null     float64
 1   AMD     61 non-null     float64
 2   AMZN    61 non-null     float64
 3   BA      61 non-null     float64
 4   CRM     61 non-null     float64
 5   GOOGL   61 non-null     float64
 6   JNJ     61 non-null     float64
 7   KO      61 non-null     float64
 8   MA      61 non-null     float64
 9   META    61 non-null     float64
 10  MSFT    61 non-null     float64
 11  NFLX    61 non-null     float64
 12  NKE     61 non-null     float64
 13  NVDA    61 non-null     float64
 14  PEP     61 non-null     float64
 15  PG      61 non-null     float64
 16  TSLA    61 non-null     float64
 17  UNH     61 non-null     float64
 18  V       61 non-null     float64
 19  WMT     61 non-null     float64
 20  ^GSPC   61 non-null     float64
dtypes: float64(21)
memory usage: 10.5 KB

Variables:

Se usaran indicadores financieros para agrupar a las acciones:

• Rendimiento medio mensual.

• Volatilidad mensual.

• Asimetría (Skewness).

• Curtosis.

• Coeficiente Beta: mide la sensibilidad del rendimiento de una acción frente a los movimientos del mercado, indicando cuánto tiende a variar la acción en relación con el índice de referencia.

def calcular_indicadores(serie_accion, serie_indice):
    retornos = serie_accion.pct_change().dropna()
    beta = np.cov(retornos, serie_indice.pct_change().dropna())[0, 1] / np.var(serie_indice.pct_change().dropna())
    return {
        'Retorno': retornos.mean(),
        'Volatilidad': retornos.std(),
        'Skewness': retornos.skew(),
        'Kurtosis': retornos.kurt(),
        'Beta': beta
    }

caracteristicas = []
for accion in acciones:
    caracteristicas.append(calcular_indicadores(datos[accion], datos[indice]))

df_indicadores = pd.DataFrame(caracteristicas, index=acciones)

df_indicadores.describe()

	Retorno	Volatilidad	Skewness	Kurtosis	Beta
count	20.000000	20.000000	20.000000	20.000000	20.000000
mean	0.016279	0.092425	0.051634	0.542926	1.153155
std	0.013544	0.041562	0.562000	1.361423	0.589540
min	0.001234	0.045147	-1.143828	-0.827875	0.392903
25%	0.008797	0.062848	-0.288276	-0.358967	0.615435
50%	0.012891	0.079984	0.123930	-0.230200	1.125788
75%	0.020063	0.119030	0.306697	1.171872	1.420759
max	0.058650	0.203409	1.035206	4.428854	2.369970

Matriz de correlación:

# Matriz de correlación entre las variables:
import seaborn as sns

plt.figure(figsize=(8, 6))
sns.heatmap(df_indicadores.corr(), annot=True, cmap='coolwarm', fmt=".2f", linewidths=.5)
plt.title('Mapa de Calor de Correlaciones de Indicadores')
plt.show()

Pair plot:

sns.pairplot(df_indicadores, diag_kind='kde')
plt.suptitle('Indicadores', y=1.02)
plt.show()

# Visualización 3D de los indicadores usando px.scatter_3d:
import plotly.express as px

fig = px.scatter_3d(
    df_indicadores,
    x='Retorno',
    y='Volatilidad',
    z='Skewness',
    opacity=0.7,
    title='Indicadores Financieros 3D'
)

fig.update_layout(
    scene=dict(
        xaxis_title='Retorno',
        yaxis_title='Volatilidad',
        zaxis_title='Skewness'
    )
)

fig.show()

fig = px.scatter_3d(
    df_indicadores,
    x='Retorno',
    y='Volatilidad',
    z='Skewness',
    color='Beta', # Para clasificar por Beta
    opacity=0.7,
    title='Indicadores Financieros 3D'
)

fig.update_layout(
    scene=dict(
        xaxis_title='Retorno',
        yaxis_title='Volatilidad',
        zaxis_title='Skewness'
    )
)

fig.show()

K-Means:

from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans, DBSCAN
from sklearn.metrics import silhouette_score, pairwise_distances_argmin_min
from scipy.cluster.hierarchy import dendrogram, linkage, fcluster

df_indicadores.columns

Index(['Retorno', 'Volatilidad', 'Skewness', 'Kurtosis', 'Beta'], dtype='object')

variables = ['Retorno', 'Volatilidad', 'Skewness', 'Kurtosis', 'Beta']

df = df_indicadores[variables]

scaler = StandardScaler()
X_scaled = scaler.fit_transform(df)

# Calcular WCSS para diferentes valores de K:
wcss = []
K = range(1, 10)
for k in K:
    kmeans = KMeans(n_clusters=k, random_state=34)
    kmeans.fit(X_scaled)
    wcss.append(kmeans.inertia_)

# Visualizar el método del codo
plt.figure(figsize=(8, 4))
plt.plot(K, wcss, "bo-")
plt.xlabel("Número de clústeres (K)")
plt.ylabel("WCSS")
plt.title("Método del Codo para determinar el número óptimo de clústeres")
plt.show()

!pip install kneed -q

# Seleccion "automatica" del punto de codo:

# !pip install kneed

from kneed import KneeLocator

kl = KneeLocator(
    range(1,10),
    wcss,
    curve="convex",
    direction="decreasing"
)

print(kl.elbow)

5

# Calcular la puntuación de la silueta para diferentes valores de K:
from sklearn.metrics import silhouette_score

silhouette_scores = []
K = range(2, 11)
for k in K:
    kmeans = KMeans(n_clusters=k, random_state=34)
    kmeans.fit(X_scaled)
    labels = kmeans.labels_
    score = silhouette_score(X_scaled, labels)
    silhouette_scores.append(score)

# Visualizar la puntuación de la silueta
plt.figure(figsize=(8, 4))
plt.plot(K, silhouette_scores, "bo-")
plt.xlabel("Número de clústeres (K)")
plt.ylabel("Puntuación de la Silueta")
plt.title("Método de la Silueta para determinar el número óptimo de clústeres")
plt.show()

Clusters = 3

k_base = 3

kmeans = KMeans(n_clusters=k_base, random_state=34)
df['Cluster_KMeans'] = kmeans.fit_predict(X_scaled)

# Valores de Inercia y Silueta:
inercia = kmeans.inertia_
silhouette = silhouette_score(X_scaled, df['Cluster_KMeans'])

print(f"Clusters: {k_base}")
print(f"Inercia: {inercia}")
print(f"Puntuación de la Silueta: {silhouette}")

Clusters: 3
Inercia: 43.04523400207732
Puntuación de la Silueta: 0.38199684578471965

sns.pairplot(df, hue='Cluster_KMeans', diag_kind='kde', palette='Set1')
plt.suptitle('Clustering K-Means', y=1.02)
plt.show()

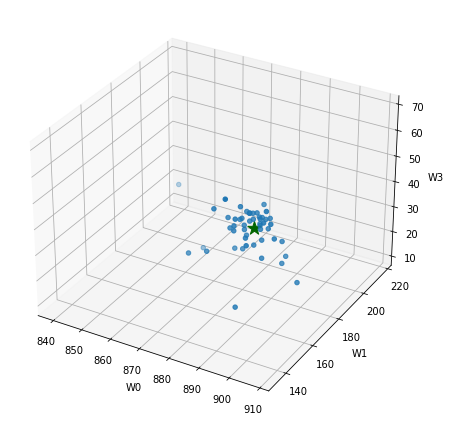
# Visualización 3D de los clusters usando px.scatter_3d:

fig = px.scatter_3d(
    df,
    x='Retorno',
    y='Volatilidad',
    z='Beta',
    color='Cluster_KMeans',
    opacity=0.7,
    title='Clustering K-Means 3D'
)

fig.update_layout(
    scene=dict(
        xaxis_title='Retorno',
        yaxis_title='Volatilidad',
        zaxis_title='Beta'
    )
)

fig.show()

from itertools import combinations
import plotly.graph_objects as go
from plotly.subplots import make_subplots
from plotly.express.colors import qualitative as qcolors

def plot_3d_combinations(df,
                         indicadores=('Retorno','Volatilidad','Skewness','Kurtosis','Beta'),
                         cluster_col='Cluster_KMeans',
                         rows=2,
                         marker_size=4,
                         opacity=0.8):
    # Combinaciones 3D
    combos = list(combinations(indicadores, 3))
    cols = int(np.ceil(len(combos)/rows))

    # Paleta discreta para clusters
    clusters = df[cluster_col].astype(str)
    cluster_vals = clusters.unique()
    color_map = {cl: qcolors.Plotly[i % len(qcolors.Plotly)] for i, cl in enumerate(sorted(cluster_vals))}

    # Lienzo con subplots 3D
    fig = make_subplots(
        rows=rows, cols=cols,
        specs=[[{'type': 'scene'} for _ in range(cols)] for _ in range(rows)],
        subplot_titles=[f"{x} vs {y} vs {z}" for (x,y,z) in combos]
    )

    # Añadir trazas por subplot y por cluster (para leyenda discreta)
    for i, (x, y, z) in enumerate(combos, start=1):
        r = (i-1)//cols + 1
        c = (i-1)%cols + 1

        for cl in sorted(cluster_vals):
            mask = clusters == cl
            fig.add_trace(
                go.Scatter3d(
                    x=df.loc[mask, x],
                    y=df.loc[mask, y],
                    z=df.loc[mask, z],
                    mode='markers',
                    name=f"Cluster {cl}",
                    legendgroup=f"Cluster {cl}",
                    showlegend=(i == 1),  # leyenda solo en el primer subplot
                    marker=dict(size=marker_size, opacity=opacity, color=color_map[cl]),
                    hovertemplate=f"{x}: %{{x}}<br>{y}: %{{y}}<br>{z}: %{{z}}<br>Cluster: {cl}<extra></extra>"
                ),
                row=r, col=c
            )

        # Títulos de ejes para cada escena
        scene_id = "scene" if i == 1 else f"scene{i}"
        fig.layout[scene_id].xaxis.title = x
        fig.layout[scene_id].yaxis.title = y
        fig.layout[scene_id].zaxis.title = z

    fig.update_layout(
        height=800, width=1700,
        title_text="Clustering K-Means 3D — Todas las combinaciones de indicadores",
        margin=dict(l=0, r=0, t=50, b=0)
    )
    fig.show()

plot_3d_combinations(df)

def graficar_clusters(df, metodo, var_x='Volatilidad', var_y='Retorno'):
    plt.figure(figsize=(10, 6))
    sns.scatterplot(
        data=df,
        x=var_x,
        y=var_y,
        hue=f'Cluster_{metodo}',
        palette='Set1',
        s=120
    )
    for i in range(len(df)):
        plt.text(df[var_x].iloc[i] + 0.002, df[var_y].iloc[i], df.index[i], fontsize=9)

    plt.title(f'Clustering por {metodo}: {var_y} vs {var_x}')
    plt.xlabel(var_x)
    plt.ylabel(var_y)
    plt.legend(title='Cluster')
    plt.grid(True)
    plt.show()

# Graficar cada método
graficar_clusters(df, 'KMeans')

# Clustering y variables en escala estandarizada:
labels = kmeans.labels_
X_scaled_df = pd.DataFrame(X_scaled, columns=df.iloc[:,:-1].columns)
X_scaled_df['Cluster_KMeans'] = labels

import plotly.graph_objects as go

# Columnas a usar
cols = ['Retorno','Volatilidad','Skewness','Kurtosis','Beta']

# Preparar datos y calcular promedio por cluster
tmp = X_scaled_df.copy()
tmp[cols] = tmp[cols].apply(pd.to_numeric, errors='coerce')
agg = tmp.groupby('Cluster_KMeans')[cols].mean().sort_index()

# Construir radar combinado
cats = cols + [cols[0]]
fig = go.Figure()

for cl, row in agg.iterrows():
    vals = row.tolist()
    fig.add_trace(go.Scatterpolar(
        r=vals + [vals[0]],
        theta=cats,
        name=f'Cluster {cl}',
        fill='toself',
        opacity=0.30
    ))

fig.update_layout(
    title='Radar combinado por cluster',
    template='plotly_white',
    polar=dict(radialaxis=dict(showline=False, gridcolor='lightgray'))
)

fig.show()

import math

def boxplots_por_cluster(df):
    """
    Genera boxplots para cada variable numérica en df agrupando por Cluster_KMeans,
    mostrando 3 gráficos por fila.

    Parámetros:
    -----------
    df : pandas.DataFrame
        DataFrame con las columnas numéricas y la columna 'Cluster_KMeans'.
    """

    # Variables numéricas (todas menos Cluster_KMeans)
    variables_numericas = [col for col in df.columns if col != 'Cluster_KMeans']

    # Número de filas necesarias (3 gráficos por fila)
    n_vars = len(variables_numericas)
    n_cols = 3
    n_rows = math.ceil(n_vars / n_cols)

    # Crear figura
    fig, axes = plt.subplots(n_rows, n_cols, figsize=(n_cols * 5, n_rows * 4))
    axes = axes.flatten()

    for i, col in enumerate(variables_numericas):
        sns.boxplot(
            data=df,
            x='Cluster_KMeans',
            y=col,
            hue='Cluster_KMeans',   # Para evitar el FutureWarning
            palette='Set2',
            legend=False,
            ax=axes[i]
        )
        axes[i].set_title(f'Boxplot de {col} por Cluster', fontsize=12)
        axes[i].set_xlabel('Cluster')
        axes[i].set_ylabel(col)

    # Ocultar ejes vacíos si sobran
    for j in range(i+1, len(axes)):
        axes[j].axis('off')

    plt.tight_layout()
    plt.show()

boxplots_por_cluster(df)

¿Cómo cambian los resultados con 3 clusters?

¿Cómo cambian los resultados con solo las variables Skewness y Kurtosis?

Analizar CMR con BA

¿Qué tiene de característico NFLX?

¿Es posible agrupar en un mismo clusters las acciones de baja volatilidad y rendimientos con las acciones más agresivas?