Ajuste SARIMA precio de electricidad#
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from scipy.stats import boxcox
from statsmodels.tsa.statespace.sarimax import SARIMAX
import statsmodels.api as sm
from scipy.stats import norm
Funciones#
def plot_serie_tiempo(
serie: pd.DataFrame,
nombre: str,
unidades: str = None,
columna: str = None,
fecha_inicio: str = None,
fecha_fin: str = None,
color: str = 'navy',
linewidth: float = 2,
num_xticks: int = 12,
estacionalidad: str = None, # 'diciembre', 'enero', 'semana', 'semestre', 'custom_month'
custom_month: int = None, # Si quieres marcar otro mes (ejemplo: 3 para marzo)
vline_label: str = None, # Etiqueta para la(s) línea(s) vertical(es)
hlines: list = None, # lista de valores horizontales a marcar
hlines_labels: list = None, # lista de etiquetas para líneas horizontales
color_estacion: str = 'darkgray', # color de las líneas estacionales
alpha_estacion: float = 0.3, # transparencia de líneas estacionales
color_hline: str = 'gray', # color de las líneas horizontales
alpha_hline: float = 0.7 # transparencia de líneas horizontales
):
"""
Gráfico elegante de serie de tiempo.
- Eje X alineado con la primera fecha real de la serie.
- Opcional: marcar estacionalidades (diciembres, semanas, semestres, mes personalizado) con etiqueta.
- Líneas horizontales con etiqueta opcional (legend).
"""
df = serie.copy()
if columna is None:
columna = df.columns[0]
if fecha_inicio:
df = df[df.index >= fecha_inicio]
if fecha_fin:
df = df[df.index <= fecha_fin]
# Asegura que el índice sea datetime y esté ordenado
df = df.sort_index()
df.index = pd.to_datetime(df.index)
plt.style.use('ggplot')
fig, ax = plt.subplots(figsize=(14, 6))
# Gráfica principal
ax.plot(df.index, df[columna], color=color, linewidth=linewidth, label=nombre)
ax.set_title(f"Serie de tiempo: {nombre}", fontsize=20, weight='bold',
color='black')
ax.set_xlabel("Fecha", fontsize=15, color='black')
ax.set_ylabel(unidades, fontsize=15, color='black')
ax.tick_params(axis='both', colors='black', labelsize=13)
for label in ax.get_xticklabels() + ax.get_yticklabels():
label.set_color('black')
# Limita el rango del eje X exactamente al rango de fechas de la serie (no corrido)
ax.set_xlim(df.index.min(), df.index.max())
# Ticks equidistantes en eje X, asegurando que empieza en la primera fecha
idx = df.index
if len(idx) > num_xticks:
ticks = np.linspace(0, len(idx)-1, num_xticks, dtype=int)
ticks[0] = 0 # asegúrate que arranque en la primera fecha
ticklabels = [idx[i] for i in ticks]
ax.set_xticks(ticklabels)
ax.set_xticklabels([pd.to_datetime(t).strftime('%b %Y') for t in ticklabels], rotation=0, color='black')
else:
ax.xaxis.set_major_formatter(mdates.DateFormatter('%b %Y'))
fig.autofmt_xdate(rotation=0)
# ==============================
# LÍNEAS VERTICALES: Estacionalidad (con etiqueta en leyenda si se desea)
# ==============================
vlines_plotted = False
if estacionalidad is not None:
if estacionalidad == 'diciembre':
fechas_mark = df[df.index.month == 12].index
elif estacionalidad == 'enero':
fechas_mark = df[df.index.month == 1].index
elif estacionalidad == 'semana':
fechas_mark = df[df.index.weekday == 0].index
elif estacionalidad == 'semestre':
fechas_mark = df[df.index.month.isin([6, 12])].index
elif estacionalidad == 'custom_month' and custom_month is not None:
fechas_mark = df[df.index.month == custom_month].index
else:
fechas_mark = []
for i, f in enumerate(fechas_mark):
# Solo pone la etiqueta una vez (la primera línea)
if not vlines_plotted and vline_label is not None:
ax.axvline(f, color=color_estacion, alpha=alpha_estacion, linewidth=2, linestyle='--', zorder=0, label=vline_label)
vlines_plotted = True
else:
ax.axvline(f, color=color_estacion, alpha=alpha_estacion, linewidth=2, linestyle='--', zorder=0)
# ==============================
# LÍNEAS HORIZONTALES OPCIONALES, con leyenda
# ==============================
if hlines is not None:
if hlines_labels is None:
hlines_labels = [None] * len(hlines)
for i, h in enumerate(hlines):
if hlines_labels[i] is not None:
ax.axhline(h, color=color_hline, alpha=alpha_hline, linewidth=1.5, linestyle='--', zorder=0, label=hlines_labels[i])
else:
ax.axhline(h, color=color_hline, alpha=alpha_hline, linewidth=1.5, linestyle='--', zorder=0)
# Coloca la leyenda solo si hay etiquetas
handles, labels = ax.get_legend_handles_labels()
if any(labels):
ax.legend(loc='best', fontsize=13, frameon=True)
ax.grid(True, alpha=0.4)
plt.tight_layout()
plt.show()
##################################################################################
def analisis_estacionariedad_full(
serie: pd.Series,
nombre: str = None,
lags: int = 24,
xtick_interval: int = 3
):
"""
Gráfica y análisis de estacionariedad para una serie de tiempo con múltiples transformaciones:
- Serie original
- Diferenciación
- Logaritmo
- Diferenciación del Logaritmo
- Raíz cuadrada
- Diferenciación de la raíz cuadrada
- Box-Cox (con corrimiento si hay valores <= 0)
- Diferenciación del Box-Cox
Para cada transformación se grafica:
- Serie transformada en el tiempo
- ACF
- PACF
- Resultado de la prueba ADF con interpretación
Args:
serie: Serie de tiempo (índice datetime, pandas.Series)
nombre: Nombre de la serie (para títulos)
lags: Número de rezagos para ACF/PACF
xtick_interval: Mostrar ticks en X cada este número de lags, incluyendo siempre el lag 1
Return:
dict con los resultados de la ADF para cada transformación
"""
if nombre is None:
nombre = serie.name if serie.name is not None else "Serie"
serie = serie.astype(float).copy()
serie_orig = serie.copy()
serie_diff = serie_orig.diff().dropna()
# Logaritmo
if (serie_orig <= 0).any():
log_ok = False
serie_log = pd.Series([np.nan]*len(serie_orig), index=serie_orig.index)
serie_log_diff = pd.Series([np.nan]*len(serie_orig), index=serie_orig.index)
else:
log_ok = True
serie_log = np.log(serie_orig)
serie_log_diff = serie_log.diff().dropna()
# Raíz cuadrada
if (serie_orig < 0).any():
sqrt_ok = False
serie_sqrt = pd.Series([np.nan]*len(serie_orig), index=serie_orig.index)
serie_sqrt_diff = pd.Series([np.nan]*len(serie_orig), index=serie_orig.index)
else:
sqrt_ok = True
serie_sqrt = np.sqrt(serie_orig)
serie_sqrt_diff = serie_sqrt.diff().dropna()
# Box–Cox
if (serie_orig <= 0).any():
shift_bc = 1 - serie_orig.min()
else:
shift_bc = 0.0
serie_bc_input = serie_orig + shift_bc
if (serie_bc_input <= 0).any():
bc_ok = False
serie_boxcox = pd.Series([np.nan]*len(serie_orig), index=serie_orig.index)
serie_boxcox_diff = pd.Series([np.nan]*len(serie_orig), index=serie_orig.index)
lambda_bc = np.nan
else:
bc_ok = True
bc_vals, lambda_bc = boxcox(serie_bc_input.values)
serie_boxcox = pd.Series(bc_vals, index=serie_orig.index)
serie_boxcox_diff = serie_boxcox.diff().dropna()
# --- Títulos actualizados ---
titulos = [
f"Serie original: {nombre}",
"Diferenciación",
"Logaritmo" + ("" if log_ok else " (no aplicable)"),
"Diferenciación del Logaritmo" + ("" if log_ok else " (no aplicable)"),
"Raíz cuadrada" + ("" if sqrt_ok else " (no aplicable)"),
"Diferenciación de la raíz cuadrada" + ("" if sqrt_ok else " (no aplicable)"),
"Box-Cox" + (f" (λ = {lambda_bc:.4f})" if bc_ok else " (no aplicable)"),
"Diferenciación del Box-Cox" + ("" if bc_ok else " (no aplicable)")
]
series = [
serie_orig,
serie_diff,
serie_log,
serie_log_diff,
serie_sqrt,
serie_sqrt_diff,
serie_boxcox,
serie_boxcox_diff
]
# --- ADF ---
resultados_adf = []
interpretaciones = []
for i, s in enumerate(series):
s_ = s.dropna()
if len(s_) < 5:
resultados_adf.append((np.nan, np.nan))
interpretaciones.append("No evaluable")
continue
regression_type = 'ct' if i in [0, 2, 4, 6] else 'c'
try:
adf_res = adfuller(s_, regression=regression_type, autolag='AIC')
estadistico = adf_res[0]
pvalue = adf_res[1]
except Exception:
estadistico = np.nan
pvalue = np.nan
resultados_adf.append((estadistico, pvalue))
interpretaciones.append("Estacionaria" if (pvalue is not None and pvalue < 0.05) else "No estacionaria")
# --- Gráficos ---
filas = len(series)
fig, axes = plt.subplots(filas, 3, figsize=(18, 4*filas), squeeze=False)
colores = ['black'] * filas
for fila in range(filas):
serie_fila = series[fila]
# Serie temporal
axes[fila, 0].plot(serie_fila, color=colores[fila], lw=1)
axes[fila, 0].set_title(titulos[fila], color='black')
axes[fila, 0].set_xlabel("Fecha", color='black')
if fila == 0:
ylabel = "Valor"
elif fila == 1:
ylabel = "Δ Valor"
elif fila == 2:
ylabel = "Log(Valor)"
elif fila == 3:
ylabel = "Δ Log(Valor)"
elif fila == 4:
ylabel = "√Valor"
elif fila == 5:
ylabel = "Δ √Valor"
elif fila == 6:
ylabel = "Box-Cox"
else:
ylabel = "Δ Box-Cox"
axes[fila, 0].set_ylabel(ylabel, color='black')
axes[fila, 0].grid(True, alpha=0.3)
axes[fila, 0].tick_params(axis='both', labelsize=11, colors='black')
adf_est, adf_p = resultados_adf[fila]
axes[fila, 0].text(
0.02, 0.85,
f"ADF: {adf_est:.2f}\np-valor: {adf_p:.4f}\n{interpretaciones[fila]}",
transform=axes[fila, 0].transAxes,
fontsize=11,
bbox=dict(facecolor='white', alpha=0.85),
color='black'
)
# ACF
try:
plot_acf(serie_fila.dropna(), lags=lags, ax=axes[fila, 1], zero=False, color=colores[fila])
except Exception:
axes[fila, 1].text(0.5, 0.5, "ACF no disponible", ha='center', va='center')
axes[fila, 1].set_title("ACF", color='black')
xticks = [1] + list(range(xtick_interval, lags + 1, xtick_interval))
axes[fila, 1].set_xticks(sorted(set(xticks)))
axes[fila, 1].tick_params(axis='both', labelsize=11, colors='black')
axes[fila, 1].set_xlabel("Lag", color='black')
# PACF
try:
plot_pacf(serie_fila.dropna(), lags=lags, ax=axes[fila, 2], zero=False, color=colores[fila])
except Exception:
axes[fila, 2].text(0.5, 0.5, "PACF no disponible", ha='center', va='center')
axes[fila, 2].set_title("PACF", color='black')
axes[fila, 2].set_xticks(sorted(set(xticks)))
axes[fila, 2].tick_params(axis='both', labelsize=11, colors='black')
axes[fila, 2].set_xlabel("Lag", color='black')
plt.tight_layout()
plt.show()
# --- Resumen ADF ---
adf_dict = {
titulos[i]: {
"estadístico ADF": resultados_adf[i][0],
"p-valor": resultados_adf[i][1],
"interpretación": interpretaciones[i],
"nota_boxcox": (
f"lambda Box-Cox = {lambda_bc:.4f}, shift aplicado = {shift_bc:.4f}"
if ("Box-Cox" in titulos[i] and bc_ok)
else ("Box-Cox no aplicable" if "Box-Cox" in titulos[i] and not bc_ok else None)
)
}
for i in range(filas)
}
return adf_dict
##################################################################################
def analisis_residuales(
residuals,
nombre: str = "Serie de tiempo",
lags: int = 24,
color_resid: str = "navy",
color_qq: str = "navy",
color_acf_pacf: str = "navy"
):
"""
Análisis gráfico de residuales:
- Residuales en el tiempo (toda la fila superior)
- Histograma + curva normal (izq), QQ-plot (der)
- ACF (izq), PACF (der) con bandas y barras color navy
"""
residuals = residuals[1:].dropna()
mu = residuals.mean()
sigma = residuals.std(ddof=1)
x = np.linspace(residuals.min(), residuals.max(), 400)
pdf = norm.pdf(x, loc=mu, scale=sigma)
fig = plt.figure(constrained_layout=True, figsize=(14, 11))
gs = fig.add_gridspec(3, 2, height_ratios=[1, 1, 1])
# 1. Residuales en el tiempo
ax_time = fig.add_subplot(gs[0, :])
ax_time.scatter(residuals.index, residuals, color=color_resid, alpha=0.7, s=20)
ax_time.axhline(0, ls="--", color="black")
ax_time.set_title(f"Residuales en el tiempo: {nombre}", color='black')
ax_time.set_xlabel("Tiempo", color='black')
ax_time.set_ylabel("Residual", color='black')
ax_time.tick_params(axis='both', labelsize=11, colors='black')
# 2. Histograma + curva Normal
ax_hist = fig.add_subplot(gs[1, 0])
ax_hist.hist(residuals, bins="auto", density=True, alpha=0.6, edgecolor="k", color="royalblue")
ax_hist.plot(x, pdf, lw=2, label=f"N({mu:.3f}, {sigma:.3f}²)", color="darkred")
ax_hist.set_title("Histograma residuaes y ajuste Normal", color='black')
ax_hist.set_xlabel("Residual", color='black')
ax_hist.set_ylabel("Densidad", color='black')
ax_hist.legend(fontsize=9)
ax_hist.grid(alpha=0.18)
ax_hist.tick_params(axis='both', labelsize=10, colors='black')
# 3. QQ-plot
ax_qq = fig.add_subplot(gs[1, 1])
qq = sm.qqplot(residuals, line='45', fit=True, ax=ax_qq, markerfacecolor=color_qq, markeredgecolor=color_qq, marker='o')
lines = ax_qq.get_lines()
if len(lines) >= 1:
lines[0].set_color(color_qq)
lines[0].set_marker('o')
lines[0].set_linestyle('None')
if len(lines) >= 2:
lines[1].set_color("black")
lines[1].set_linestyle("--")
ax_qq.set_title("Q-Q Plot de los residuales", color='black')
ax_qq.set_xlabel("Cuantiles teóricos (Normal)", color='black')
ax_qq.set_ylabel("Cuantiles de los residuales", color='black')
ax_qq.tick_params(axis='both', labelsize=10, colors='black')
for l in ax_qq.get_xticklabels() + ax_qq.get_yticklabels():
l.set_color('black')
# 4. ACF (usando color navy en barras y bandas)
ax_acf = fig.add_subplot(gs[2, 0])
sm.graphics.tsa.plot_acf(residuals, lags=lags, ax=ax_acf, zero=False, color=color_acf_pacf)
ax_acf.set_title("ACF de los residuales", color='black')
ax_acf.set_xlabel("Rezagos", color='black')
ax_acf.set_ylabel("Autocorrelación", color='black')
ax_acf.tick_params(axis='both', labelsize=10, colors='black')
# 5. PACF (usando color navy en barras y bandas)
ax_pacf = fig.add_subplot(gs[2, 1])
sm.graphics.tsa.plot_pacf(residuals, lags=lags, ax=ax_pacf, zero=False, color=color_acf_pacf)
ax_pacf.set_title("PACF de los residuales", color='black')
ax_pacf.set_xlabel("Rezagos", color='black')
ax_pacf.set_ylabel("Autocorrelación parcial", color='black')
ax_pacf.tick_params(axis='both', labelsize=10, colors='black')
plt.show()
return
##################################################################################
def analizar_ajuste_serie(
serie_original,
fitted_values,
results,
test,
n_forecast,
transformacion=None, # 'log', 'boxcox', 'sqrt', o None
lambda_bc=None, # solo si boxcox
nombre="Serie"
):
"""
Analiza el ajuste de un modelo y grafica ajuste+pronóstico sobre la serie original,
devolviendo predicciones revertidas a la escala original.
Args:
serie_original: Serie original (sin transformar, index datetime)
fitted_values: Serie de fittedvalues (en escala transformada)
results: Modelo ajustado de statsmodels (debe soportar .append, .get_forecast)
test: Serie de test (index datetime)
n_forecast: Períodos a pronosticar por fuera de la muestra
transformacion: 'log', 'boxcox', 'sqrt' o None
lambda_bc: Valor de lambda para boxcox (si aplica)
nombre: Nombre para los ejes y leyenda
Returns:
Diccionario con:
- y_pred_train, y_pred_test, forecasting_orig, lower_bt, upper_bt
- Fechas de pronóstico futuro: future_dates
"""
# Alinear índices por seguridad
fitted_values = fitted_values.reindex(serie_original.index.intersection(fitted_values.index))
test = test.copy()
# ----------- PRONÓSTICO EN TEST (fuera de muestra, recursivo) -----------
current_results = results
forecasted_test = []
lower_ci_test = []
upper_ci_test = []
for i in range(len(test)):
forecaster = current_results.get_forecast(steps=1)
forecast_mean_test = forecaster.predicted_mean.iloc[0]
ci_i_test = forecaster.conf_int(alpha=0.05).iloc[0]
forecasted_test.append(forecast_mean_test)
lower_ci_test.append(ci_i_test.iloc[0])
upper_ci_test.append(ci_i_test.iloc[1])
# Recursivo: alimentar el modelo con el valor real observado
current_results = current_results.append(endog=[test.iloc[i]], refit=False)
forecasted_test = pd.Series(forecasted_test, index=test.index, name='forecast_test')
lower_ci_test = pd.Series(lower_ci_test, index=test.index, name='lower_test')
upper_ci_test = pd.Series(upper_ci_test, index=test.index, name='upper_test')
# ----------- PRONÓSTICO FUTURO (n_forecast meses) -----------
current_results = results.append(endog=test, refit=False)
forecasting = []
lower_ci = []
upper_ci = []
for i in range(n_forecast):
forecaster = current_results.get_forecast(steps=1)
forecast_mean = forecaster.predicted_mean.iloc[0]
ci_i = forecaster.conf_int(alpha=0.05).iloc[0]
forecasting.append(forecast_mean)
lower_ci.append(ci_i.iloc[0])
upper_ci.append(ci_i.iloc[1])
current_results = current_results.append(endog=[forecast_mean], refit=False)
# Fechas futuras mensuales (puedes personalizar)
last_date = test.index[-1]
future_dates = pd.date_range(start=last_date + pd.offsets.MonthBegin(1),
periods=n_forecast, freq='MS')
forecasting = pd.Series(forecasting, index=future_dates, name='forecast')
lower_ci = pd.Series(lower_ci, index=future_dates, name='lower')
upper_ci = pd.Series(upper_ci, index=future_dates, name='upper')
# ----------- REVERSIÓN DE TRANSFORMACIÓN -----------
if transformacion == "log":
y_pred_train = np.exp(fitted_values)
y_pred_test = np.exp(forecasted_test)
forecasting_orig = np.exp(forecasting)
lower_bt = np.exp(lower_ci)
upper_bt = np.exp(upper_ci)
elif transformacion == "boxcox":
if lambda_bc is None:
raise ValueError("Debes indicar lambda_bc para la transformación Box-Cox")
y_pred_train = np.power((lambda_bc * fitted_values + 1), 1 / lambda_bc)
y_pred_test = np.power((lambda_bc * forecasted_test + 1), 1 / lambda_bc)
forecasting_orig = np.power((lambda_bc * forecasting + 1), 1 / lambda_bc)
lower_bt = np.power((lambda_bc * lower_ci + 1), 1 / lambda_bc)
upper_bt = np.power((lambda_bc * upper_ci + 1), 1 / lambda_bc)
elif transformacion == "sqrt":
y_pred_train = fitted_values ** 2
y_pred_test = forecasted_test ** 2
forecasting_orig = forecasting ** 2
lower_bt = lower_ci ** 2
upper_bt = upper_ci ** 2
elif transformacion is None or transformacion == "none":
y_pred_train = fitted_values
y_pred_test = forecasted_test
forecasting_orig = forecasting
lower_bt = lower_ci
upper_bt = upper_ci
else:
raise ValueError("Transformación no soportada. Usa 'log', 'boxcox', 'sqrt' o None.")
# ----------- GRÁFICO -----------
plt.figure(figsize=(12,6))
# Serie original
plt.plot(serie_original, label=nombre, color='black')
# Ajuste en train
plt.plot(y_pred_train, label='Ajuste en train', color='tab:blue')
# Ajuste en test
plt.plot(y_pred_test, label='Pronóstico en test', color='tab:green')
# Pronóstico futuro + IC
plt.plot(forecasting_orig, label='Pronóstico futuro', color='tab:red', linestyle='--')
plt.fill_between(future_dates, lower_bt.values, upper_bt.values, color='tab:red', alpha=0.2, label='IC 95%')
plt.title(f'Ajuste y pronóstico - {nombre}')
plt.xlabel('Tiempo')
plt.ylabel('Valor')
plt.legend()
plt.tight_layout()
plt.show()
# ----------- Devuelve resultados clave -----------
return {
'y_pred_train': y_pred_train,
'y_pred_test': y_pred_test,
'forecasting_orig': forecasting_orig,
'lower_bt': lower_bt,
'upper_bt': upper_bt,
'future_dates': future_dates
}
Precio de electricidad#
# Cargar el archivo
precio_electricidad = pd.read_csv("Precio_electricidad.csv")
# Corregir nombres de columnas si tienen espacios
precio_electricidad.columns = precio_electricidad.columns.str.strip()
# Convertir 'Fecha' a datetime y usar como índice
precio_electricidad['Fecha'] = pd.to_datetime(precio_electricidad['Fecha'])
precio_electricidad.set_index('Fecha', inplace=True)
# Ordenar por fecha por si acaso
precio_electricidad = precio_electricidad.sort_index()
# Establecer frecuencia explícita para evitar el warning de statsmodels
precio_electricidad.index.freq = precio_electricidad.index.inferred_freq
precio_electricidad.head()
| Precio | |
|---|---|
| Fecha | |
| 2000-01-01 | 36.539729 |
| 2000-02-01 | 39.885205 |
| 2000-03-01 | 35.568126 |
| 2000-04-01 | 44.957443 |
| 2000-05-01 | 33.848903 |
plot_serie_tiempo(
precio_electricidad,
nombre="Precio de electricidad",
columna='Precio',
unidades='COP/kWh',
estacionalidad='diciembre',
vline_label="Diciembre",
num_xticks = 14
)
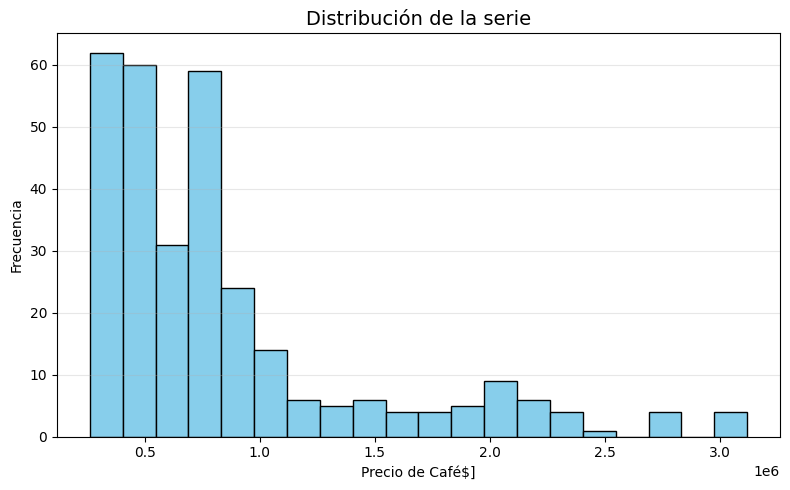
adf_resultados = analisis_estacionariedad_full(
precio_electricidad['Precio'],
nombre="Precio de electricidad",
lags=36,
xtick_interval=3
)
Transformación Box–Cox#
# Aplicar la transformación Box–Cox:
y_boxcox, lambda_bc = boxcox(precio_electricidad.iloc[:, 0])
# Convertir el resultado en pandas.Series
y_boxcox = pd.DataFrame(y_boxcox, index=precio_electricidad.index, columns=['Precio_boxcox'])
print(f"Lambda Box–Cox óptimo: {lambda_bc:.4f}")
print(y_boxcox.head())
Lambda Box–Cox óptimo: -0.3692
Precio_boxcox
Fecha
2000-01-01 1.991101
2000-02-01 2.013932
2000-03-01 1.983928
2000-04-01 2.043960
2000-05-01 1.970553
Conjunto de train y test:#
# Dividir en train y test (por ejemplo, 80% train, 20% test)
split = int(len(y_boxcox) * 0.8)
train, test = y_boxcox[:split], y_boxcox[split:]
# Graficar train y test:
plt.figure(figsize=(12, 5))
plt.plot(train, label='Train', color='navy')
plt.plot(test, label='Test', color='orange')
plt.title("Conjunto de train y test")
plt.xlabel("Fecha")
plt.ylabel("Valor")
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
import itertools
from statsmodels.tsa.statespace.sarimax import SARIMAX
Silenciar solo los warning:
import warnings
from statsmodels.tools.sm_exceptions import ConvergenceWarning
warnings.filterwarnings("ignore",
message="Non-invertible starting MA parameters",
category=UserWarning)
warnings.filterwarnings("ignore",
message="Non-stationary starting autoregressive parameters",
category=UserWarning)
warnings.filterwarnings("ignore", category=ConvergenceWarning)
Ajuste SARIMA#
El procedimiento auto-ARIMA seleccionó ARIMA(3,1,3) como especificación óptima bajo el criterio AIC. El examen de la ACF/PACF de la serie Box-Cox con d=1 muestra un pico estacional en \(s=12\) de magnitud moderada, compatible con estacionalidad mensual.
En consecuencia, es apropiado contrastar extensiones estacionales del modelo mediante \(SARIMA(3,1,3)(1,0,0)_{12}\), \(SARIMA(3,1,3)(0,0,1)_{12}\) y \(SARIMA(3,1,3)(1,0,1)_{12}\), comparando desempeño y diagnóstico de residuales.
SARIMA(3,1,3)(1,0,0,12)#
# Definir los parámetros del modelo ARIMA (p, d, q)
order = (3, 1, 3) # Puedes ajustar según el análisis de ACF y PACF
trend = 'n' # 'c' = constante, 't' = tendencia, 'ct' = constante + tendencia, 'n' = sin tendencia
seasonal_order = (1, 0, 0, 12) # Parámetros de la estacionalidad (P, D, Q, s)
# Ajustar el modelo con los datos de entrenamiento
model = SARIMAX(train, order=order, seasonal_order=seasonal_order, trend=trend)
results = model.fit()
# Mostrar resumen del modelo
print(results.summary())
SARIMAX Results
===========================================================================================
Dep. Variable: Precio_boxcox No. Observations: 232
Model: SARIMAX(3, 1, 3)x(1, 0, [], 12) Log Likelihood 411.133
Date: Fri, 07 Nov 2025 AIC -806.266
Time: 21:04:10 BIC -778.727
Sample: 01-01-2000 HQIC -795.159
- 04-01-2019
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 1.7560 0.137 12.859 0.000 1.488 2.024
ar.L2 -1.6882 0.149 -11.295 0.000 -1.981 -1.395
ar.L3 0.7459 0.101 7.368 0.000 0.547 0.944
ma.L1 -1.8682 0.147 -12.748 0.000 -2.155 -1.581
ma.L2 1.6910 0.209 8.077 0.000 1.281 2.101
ma.L3 -0.7611 0.110 -6.901 0.000 -0.977 -0.545
ar.S.L12 -0.0107 0.065 -0.165 0.869 -0.137 0.116
sigma2 0.0017 0.000 10.945 0.000 0.001 0.002
===================================================================================
Ljung-Box (L1) (Q): 0.17 Jarque-Bera (JB): 1.96
Prob(Q): 0.68 Prob(JB): 0.37
Heteroskedasticity (H): 1.63 Skew: 0.17
Prob(H) (two-sided): 0.03 Kurtosis: 3.30
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
Ajuste y pronóstico en la serie original#
fitted_values = results.fittedvalues
y_pred_train = np.power((lambda_bc * fitted_values + 1), 1 / lambda_bc)
y_pred = y_pred_train[1:]
y_real = precio_electricidad["Precio"][1:split]
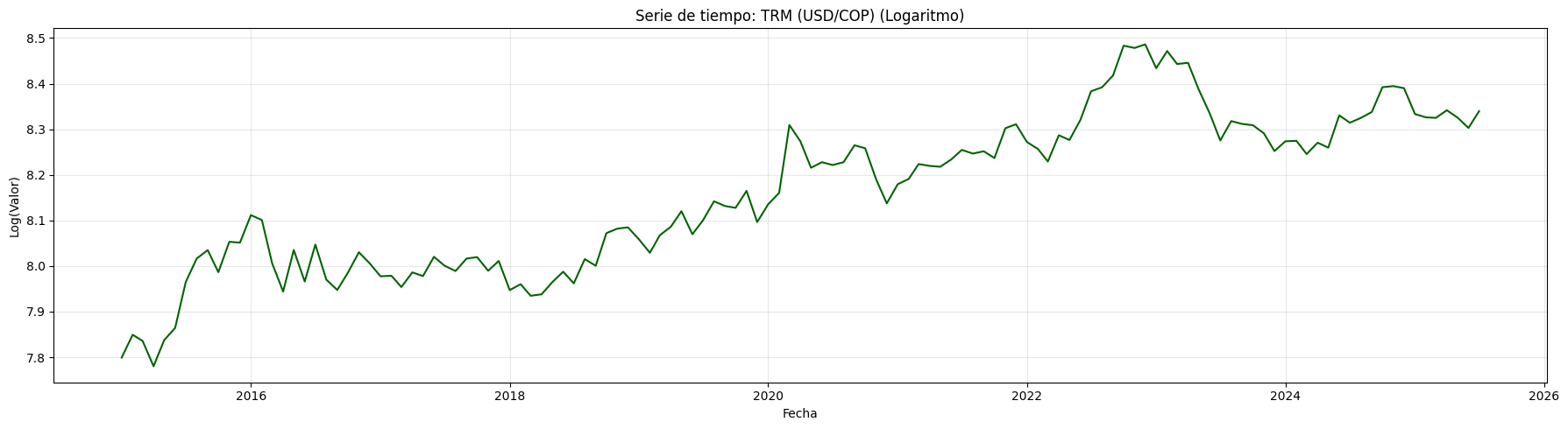
resultados = analizar_ajuste_serie(
precio_electricidad, # Serie original (sin transformar)
fitted_values, # Ajuste en train
results, # Modelo ajustado
test, # Datos test
n_forecast=12, # Periodos futuros
transformacion='boxcox', # 'log', 'boxcox', 'sqrt' o None
lambda_bc=lambda_bc, # Solo si es boxcox
nombre="Precio de electricidad"
)
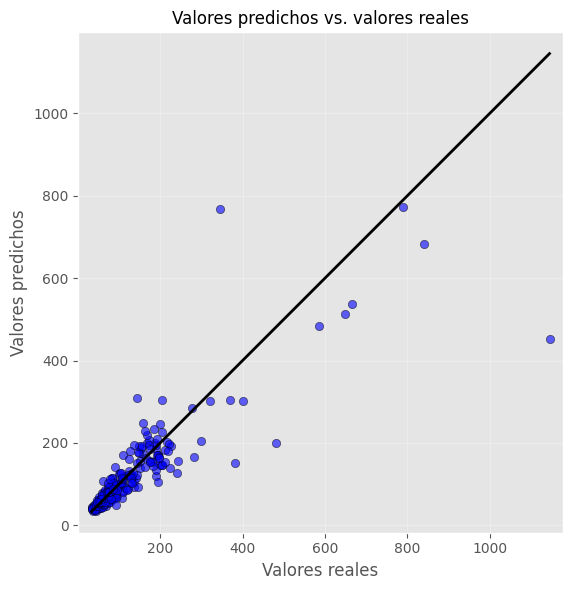
### Gráfico de valores predichos vs. valores reales
plt.figure(figsize=(6,6))
plt.scatter(y_real, y_pred, color='blue', alpha=0.6, edgecolor='k')
# Línea de identidad (y = x)
min_val = min(y_real.min(), y_pred.min())
max_val = max(y_real.max(), y_pred.max())
plt.plot([min_val, max_val], [min_val, max_val], color='black', lw=2)
plt.title("Valores predichos vs. valores reales", fontsize=12)
plt.xlabel("Valores reales")
plt.ylabel("Valores predichos")
plt.axis("equal") # asegura proporciones iguales para la diagonal
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()
Análisis de los residuales#
analisis_residuales(
results.resid, # Agregar los residuales
nombre="Precio de electricidad",
)
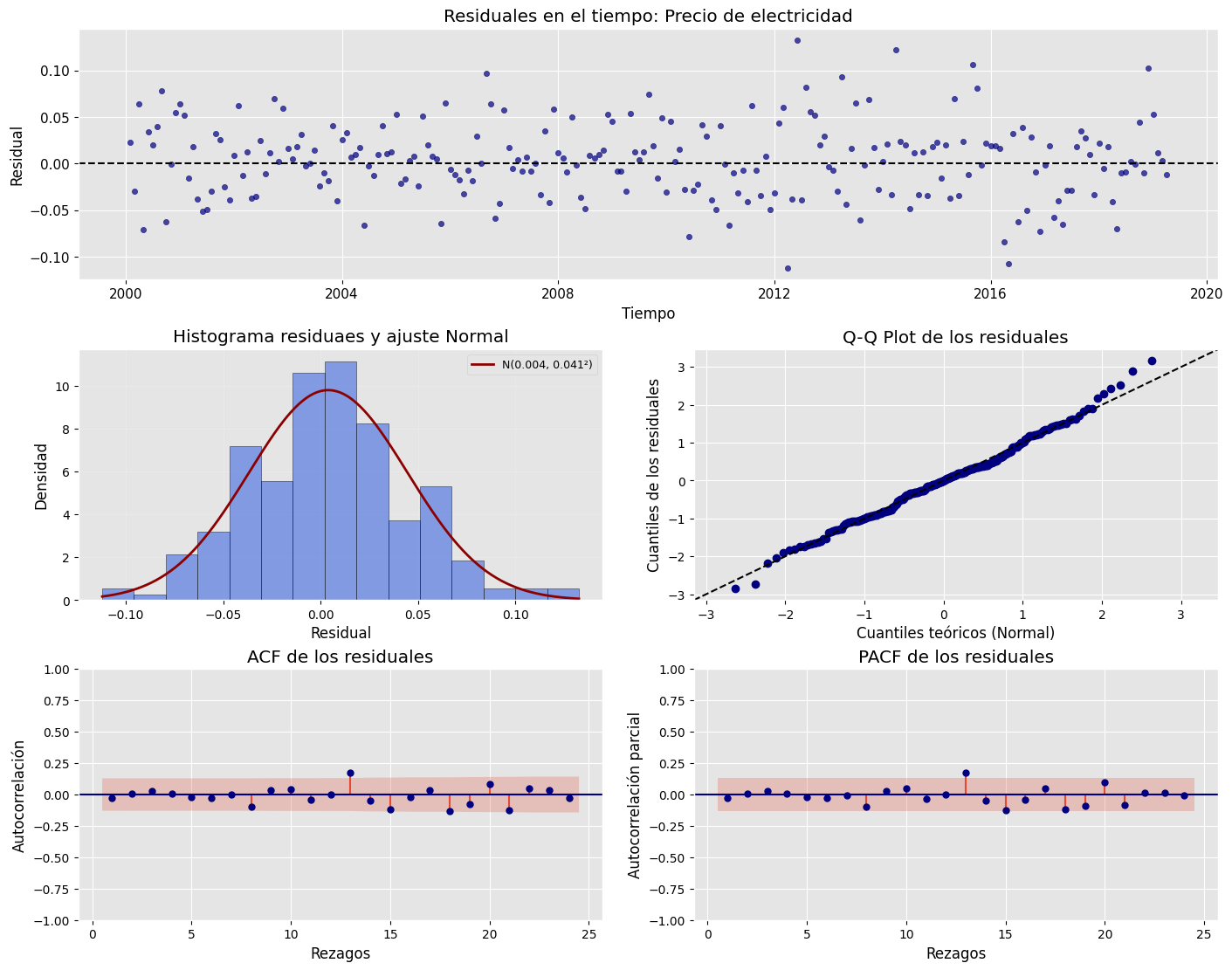
Se observa una ligera significancia en el rezago 13
SARIMA(3,1,3)(0,0,1,12)#
# Definir los parámetros del modelo ARIMA (p, d, q)
order = (3, 1, 3) # Puedes ajustar según el análisis de ACF y PACF
trend = 'n' # 'c' = constante, 't' = tendencia, 'ct' = constante + tendencia, 'n' = sin tendencia
seasonal_order = (0, 0, 1, 12) # Parámetros de la estacionalidad (P, D, Q, s)
# Ajustar el modelo con los datos de entrenamiento
model = SARIMAX(train, order=order, seasonal_order=seasonal_order, trend=trend)
results = model.fit()
# Mostrar resumen del modelo
print(results.summary())
SARIMAX Results
============================================================================================
Dep. Variable: Precio_boxcox No. Observations: 232
Model: SARIMAX(3, 1, 3)x(0, 0, [1], 12) Log Likelihood 411.683
Date: Fri, 07 Nov 2025 AIC -807.367
Time: 21:04:23 BIC -779.828
Sample: 01-01-2000 HQIC -796.259
- 04-01-2019
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 1.8172 0.088 20.761 0.000 1.646 1.989
ar.L2 -1.7691 0.098 -18.001 0.000 -1.962 -1.577
ar.L3 0.8035 0.069 11.710 0.000 0.669 0.938
ma.L1 -1.9417 0.096 -20.323 0.000 -2.129 -1.754
ma.L2 1.8184 0.150 12.130 0.000 1.525 2.112
ma.L3 -0.8393 0.081 -10.405 0.000 -0.997 -0.681
ma.S.L12 0.0113 0.063 0.180 0.857 -0.112 0.135
sigma2 0.0017 0.000 10.744 0.000 0.001 0.002
===================================================================================
Ljung-Box (L1) (Q): 0.17 Jarque-Bera (JB): 1.69
Prob(Q): 0.68 Prob(JB): 0.43
Heteroskedasticity (H): 1.62 Skew: 0.17
Prob(H) (two-sided): 0.04 Kurtosis: 3.26
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
Ajuste y pronóstico en la serie original#
fitted_values = results.fittedvalues
y_pred_train = np.power((lambda_bc * fitted_values + 1), 1 / lambda_bc)
y_pred = y_pred_train[1:]
y_real = precio_electricidad["Precio"][1:split]
resultados = analizar_ajuste_serie(
precio_electricidad, # Serie original (sin transformar)
fitted_values, # Ajuste en train
results, # Modelo ajustado
test, # Datos test
n_forecast=12, # Periodos futuros
transformacion='boxcox', # 'log', 'boxcox', 'sqrt' o None
lambda_bc=lambda_bc, # Solo si es boxcox
nombre="Precio de electricidad"
)
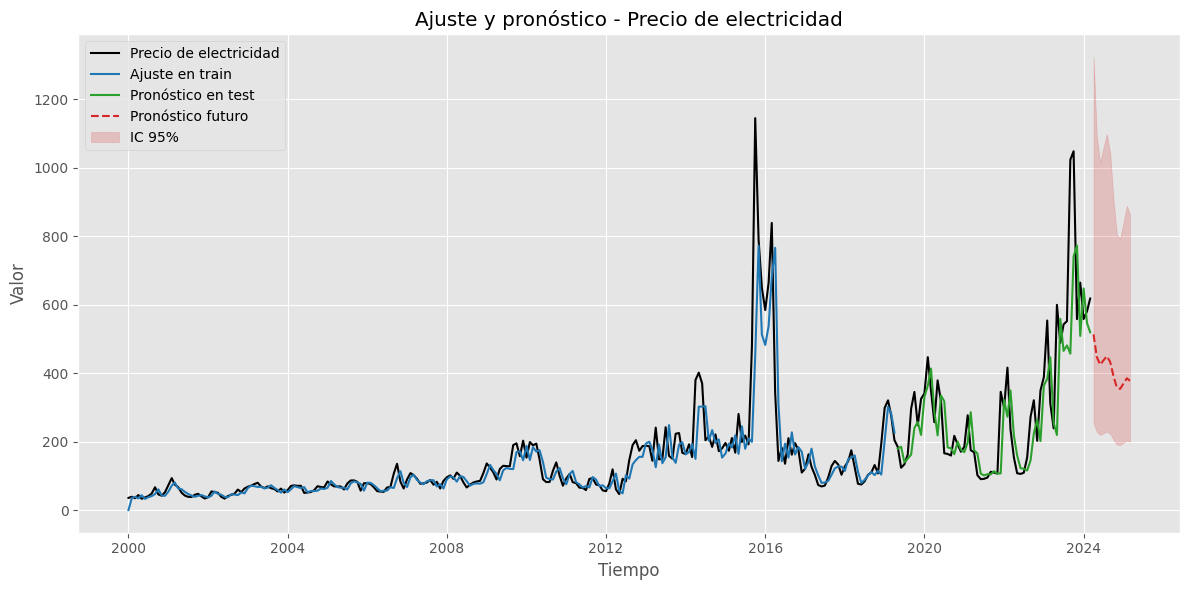
### Gráfico de valores predichos vs. valores reales
plt.figure(figsize=(6,6))
plt.scatter(y_real, y_pred, color='blue', alpha=0.6, edgecolor='k')
# Línea de identidad (y = x)
min_val = min(y_real.min(), y_pred.min())
max_val = max(y_real.max(), y_pred.max())
plt.plot([min_val, max_val], [min_val, max_val], color='black', lw=2)
plt.title("Valores predichos vs. valores reales", fontsize=12)
plt.xlabel("Valores reales")
plt.ylabel("Valores predichos")
plt.axis("equal") # asegura proporciones iguales para la diagonal
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()
Análisis de los residuales#
analisis_residuales(
results.resid, # Agregar los residuales
nombre="Precio de electricidad",
)
Se identifica una leve significancia en el rezago 13.
SARIMA(3,1,3)(1,0,1,12)#
# Definir los parámetros del modelo ARIMA (p, d, q)
order = (3, 1, 3) # Puedes ajustar según el análisis de ACF y PACF
trend = 'n' # 'c' = constante, 't' = tendencia, 'ct' = constante + tendencia, 'n' = sin tendencia
seasonal_order = (1, 0, 1, 12) # Parámetros de la estacionalidad (P, D, Q, s)
# Ajustar el modelo con los datos de entrenamiento
model = SARIMAX(train, order=order, seasonal_order=seasonal_order, trend=trend)
results = model.fit()
# Mostrar resumen del modelo
print(results.summary())
SARIMAX Results
============================================================================================
Dep. Variable: Precio_boxcox No. Observations: 232
Model: SARIMAX(3, 1, 3)x(1, 0, [1], 12) Log Likelihood 411.734
Date: Fri, 07 Nov 2025 AIC -805.469
Time: 21:04:32 BIC -774.487
Sample: 01-01-2000 HQIC -792.973
- 04-01-2019
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 1.8183 0.087 20.832 0.000 1.647 1.989
ar.L2 -1.7735 0.098 -18.106 0.000 -1.965 -1.581
ar.L3 0.8068 0.070 11.512 0.000 0.669 0.944
ma.L1 -1.9440 0.092 -21.073 0.000 -2.125 -1.763
ma.L2 1.8296 0.143 12.802 0.000 1.549 2.110
ma.L3 -0.8461 0.077 -10.997 0.000 -0.997 -0.695
ar.S.L12 0.2034 11.162 0.018 0.985 -21.674 22.080
ma.S.L12 -0.1974 11.149 -0.018 0.986 -22.048 21.653
sigma2 0.0016 0.000 9.858 0.000 0.001 0.002
===================================================================================
Ljung-Box (L1) (Q): 0.13 Jarque-Bera (JB): 1.69
Prob(Q): 0.72 Prob(JB): 0.43
Heteroskedasticity (H): 1.61 Skew: 0.17
Prob(H) (two-sided): 0.04 Kurtosis: 3.25
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
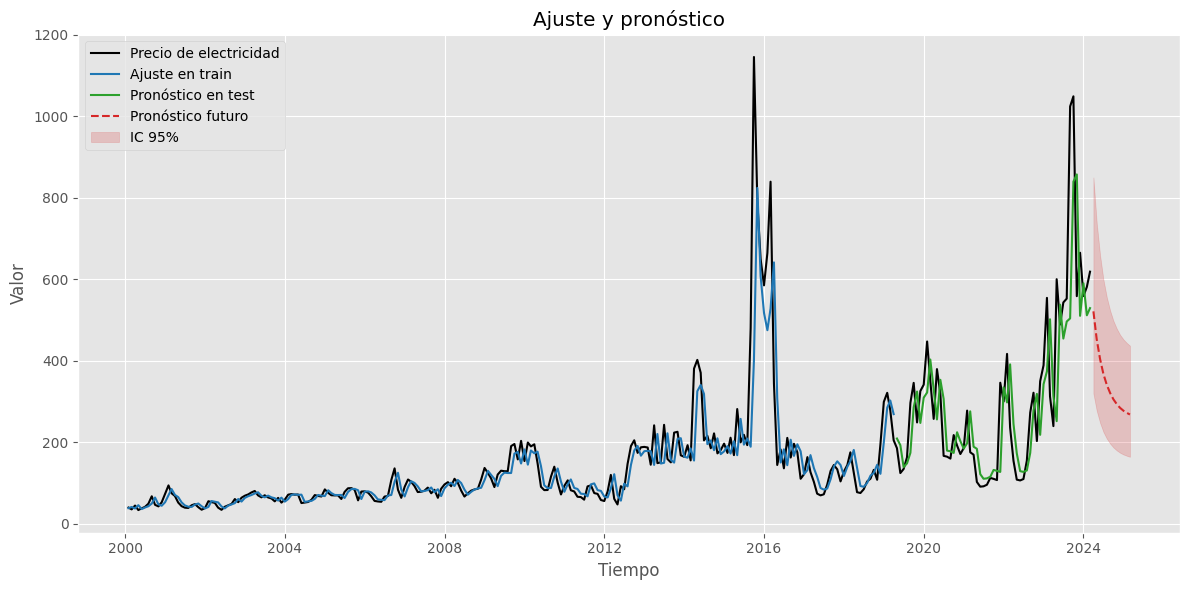
Ajuste y pronóstico en la serie original#
fitted_values = results.fittedvalues
y_pred_train = np.power((lambda_bc * fitted_values + 1), 1 / lambda_bc)
y_pred = y_pred_train[1:]
y_real = precio_electricidad["Precio"][1:split]
resultados = analizar_ajuste_serie(
precio_electricidad, # Serie original (sin transformar)
fitted_values, # Ajuste en train
results, # Modelo ajustado
test, # Datos test
n_forecast=12, # Periodos futuros
transformacion='boxcox', # 'log', 'boxcox', 'sqrt' o None
lambda_bc=lambda_bc, # Solo si es boxcox
nombre="Precio de electricidad"
)
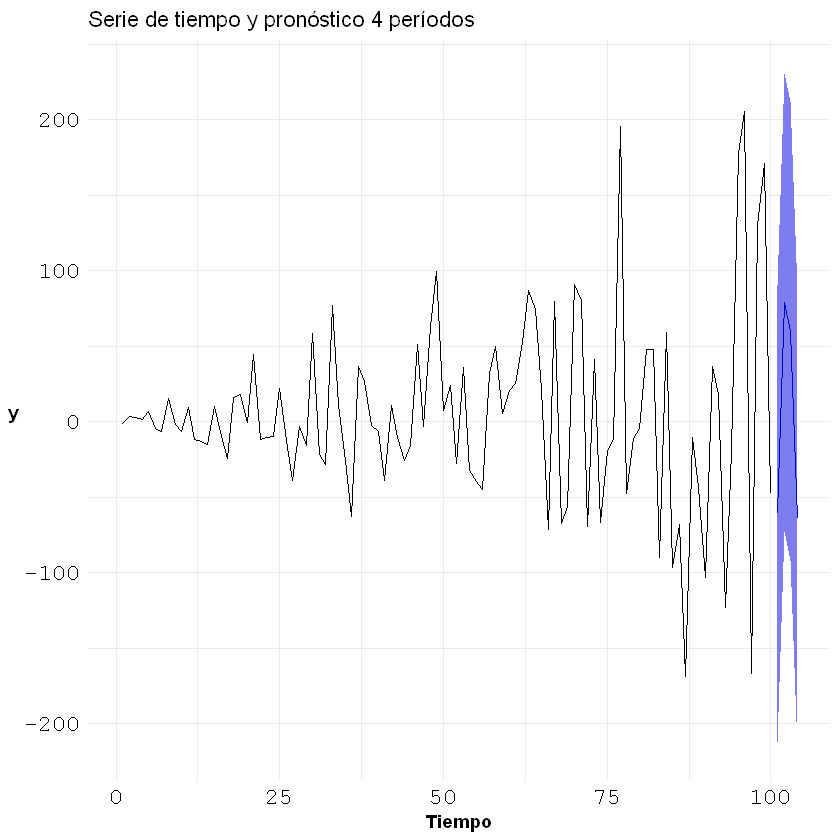
### Gráfico de valores predichos vs. valores reales
plt.figure(figsize=(6,6))
plt.scatter(y_real, y_pred, color='blue', alpha=0.6, edgecolor='k')
# Línea de identidad (y = x)
min_val = min(y_real.min(), y_pred.min())
max_val = max(y_real.max(), y_pred.max())
plt.plot([min_val, max_val], [min_val, max_val], color='black', lw=2)
plt.title("Valores predichos vs. valores reales", fontsize=12)
plt.xlabel("Valores reales")
plt.ylabel("Valores predichos")
plt.axis("equal") # asegura proporciones iguales para la diagonal
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()
Análisis de los residuales#
analisis_residuales(
results.resid, # Agregar los residuales
nombre="Precio de electricidad",
)
Se sigue observando una leve significancia en el rezago 13. Adicionalmente, el rezago 8 también muestra una significancia marginal. Por lo tanto, se ajustará el modelo SARIMA(8,1,8)(1,0,1,12) con el objetivo de que, en el análisis de los residuales, desaparezcan los rezagos significativos y así se logre un modelo que capture de manera adecuada toda la estructura temporal de la serie.
SARIMA(8,1,8)(1,0,1,12)#
# Definir los parámetros del modelo ARIMA (p, d, q)
order = (8, 1, 8) # Puedes ajustar según el análisis de ACF y PACF
trend = 'n' # 'c' = constante, 't' = tendencia, 'ct' = constante + tendencia, 'n' = sin tendencia
seasonal_order = (1, 0, 1, 12) # Parámetros de la estacionalidad (P, D, Q, s)
# Ajustar el modelo con los datos de entrenamiento
model = SARIMAX(train, order=order, seasonal_order=seasonal_order, trend=trend)
results = model.fit()
# Mostrar resumen del modelo
print(results.summary())
SARIMAX Results
============================================================================================
Dep. Variable: Precio_boxcox No. Observations: 232
Model: SARIMAX(8, 1, 8)x(1, 0, [1], 12) Log Likelihood 414.788
Date: Fri, 07 Nov 2025 AIC -791.577
Time: 21:04:43 BIC -726.171
Sample: 01-01-2000 HQIC -765.196
- 04-01-2019
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 -0.1067 0.326 -0.327 0.743 -0.745 0.532
ar.L2 -0.1240 0.275 -0.451 0.652 -0.663 0.415
ar.L3 -0.1392 0.271 -0.514 0.607 -0.669 0.391
ar.L4 0.0362 0.302 0.120 0.905 -0.557 0.629
ar.L5 -0.1889 0.214 -0.882 0.378 -0.609 0.231
ar.L6 0.0981 0.238 0.413 0.680 -0.368 0.564
ar.L7 0.2871 0.242 1.188 0.235 -0.187 0.761
ar.L8 -0.0163 0.287 -0.057 0.955 -0.578 0.546
ma.L1 -0.0245 0.318 -0.077 0.939 -0.647 0.598
ma.L2 -0.0313 0.275 -0.114 0.909 -0.570 0.507
ma.L3 -0.0238 0.292 -0.081 0.935 -0.596 0.549
ma.L4 -0.1544 0.300 -0.514 0.607 -0.743 0.434
ma.L5 0.1954 0.230 0.850 0.396 -0.255 0.646
ma.L6 -0.0797 0.256 -0.311 0.756 -0.582 0.422
ma.L7 -0.3733 0.264 -1.416 0.157 -0.890 0.143
ma.L8 -0.2459 0.309 -0.796 0.426 -0.851 0.359
ar.S.L12 0.2274 1.094 0.208 0.835 -1.918 2.372
ma.S.L12 -0.1559 1.139 -0.137 0.891 -2.389 2.077
sigma2 0.0015 0.000 10.084 0.000 0.001 0.002
===================================================================================
Ljung-Box (L1) (Q): 0.03 Jarque-Bera (JB): 0.35
Prob(Q): 0.87 Prob(JB): 0.84
Heteroskedasticity (H): 1.48 Skew: 0.09
Prob(H) (two-sided): 0.09 Kurtosis: 2.97
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
Ajuste y pronóstico en la serie original#
fitted_values = results.fittedvalues
y_pred_train = np.power((lambda_bc * fitted_values + 1), 1 / lambda_bc)
y_pred = y_pred_train[1:]
y_real = precio_electricidad["Precio"][1:split]
resultados = analizar_ajuste_serie(
precio_electricidad, # Serie original (sin transformar)
fitted_values, # Ajuste en train
results, # Modelo ajustado
test, # Datos test
n_forecast=12, # Periodos futuros
transformacion='boxcox', # 'log', 'boxcox', 'sqrt' o None
lambda_bc=lambda_bc, # Solo si es boxcox
nombre="Precio de electricidad"
)
### Gráfico de valores predichos vs. valores reales
plt.figure(figsize=(6,6))
plt.scatter(y_real, y_pred, color='blue', alpha=0.6, edgecolor='k')
# Línea de identidad (y = x)
min_val = min(y_real.min(), y_pred.min())
max_val = max(y_real.max(), y_pred.max())
plt.plot([min_val, max_val], [min_val, max_val], color='black', lw=2)
plt.title("Valores predichos vs. valores reales", fontsize=12)
plt.xlabel("Valores reales")
plt.ylabel("Valores predichos")
plt.axis("equal") # asegura proporciones iguales para la diagonal
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()
Análisis de los residuales#
analisis_residuales(
results.resid, # Agregar los residuales
nombre="Precio de electricidad",
)
Con este modelo, el análisis de los residuales confirma la ausencia de autocorrelaciones significativas, evidenciando un ajuste adecuado a la estructura temporal de la serie.