AR#
Modelos Autorregresivos AR(p)
Un modelo autorregresivo (AR) es un tipo de modelo de series de tiempo donde el valor actual de la serie depende de sus propios valores pasados más un término de error aleatorio. Se llaman autorregresivos porque la serie “se explica a sí misma” a partir de sus rezagos.
En términos simples:
\(y_t\): valor actual de la serie
\(\alpha\): constante o media ajustada \(\mu\)
\(\beta_t\) es la tendencia lineal en el tiempo
\(\phi_1, \phi_2, \dots, \phi_p\): coeficientes que indican cuánto pesa cada valor pasado
\(p\): número de rezagos que se usan (el “orden” del modelo)
\(\varepsilon_t\): error aleatorio o “ruido blanco” (media cero, varianza constante, no correlacionado)
AR(1): el caso más simple
En un AR(1) el valor actual depende solo del último valor pasado:
Si \(\phi_1\) es positivo y cercano a 1, la serie muestra mucha persistencia (los valores grandes suelen seguir a valores grandes).
Si \(\phi_1\) es negativo, la serie tiende a oscilar: un valor alto es seguido por uno bajo, y viceversa.
Si \(\phi_1 = 0\), el modelo se reduce a una serie de ruido blanco.
Este modelo es análogo a una regresión lineal simple, donde la variable dependiente es el valor actual y la variable explicativa es el valor inmediatamente anterior.
¿Para qué tipos de series de tiempo se usa?
Estacionarias en media y varianza (o que pueden hacerse estacionarias con transformaciones/ diferencias).
Sin tendencia ni estacionalidad fuerte (si existen, se suelen remover antes: diferenciar para tendencia; desestacionalizar o pasar a SARIMA).
Con memoria corta: el pasado cercano explica el presente y el efecto de choques se amortigua con el tiempo.
Propiedades básicas:
La media de la serie es constante si \(|\phi_1| < 1\).
La varianza es estable y finita bajo esa misma condición.
El efecto de un choque \(\varepsilon_t\) se diluye en el tiempo de manera exponencial.
AR(p): el caso general
Un AR(p) amplía la idea al permitir que el valor actual dependa de varios rezagos:
Es como una regresión múltiple, donde las variables explicativas son los últimos \(p\) valores de la serie. Cada coeficiente \(\phi_i\) indica cuánto influye el valor de la serie en el rezago \(i\).
Cómo se estiman los parámetros
El modelo se ajusta como una regresión:
Los residuos son:
Y se espera que se comporten como ruido blanco.
Los coeficientes se pueden estimar mediante mínimos cuadrados o máxima verosimilitud.
Analogía sencilla
Imagina que el clima de hoy depende de cómo fue el clima de los últimos días:
Si solo depende del día anterior, tenemos un AR(1).
Si además influye el clima de los últimos tres días, estamos en un AR(3).
El modelo AR “aprende” cuánto peso darle a cada día pasado para hacer una predicción del presente o del futuro.
Condición de estabilidad y el valor de φ
Para que un modelo AR(p) sea estacionario y estable, los parámetros deben cumplir ciertas condiciones.
En el caso de un AR(1):
La condición es:
¿Por qué?
Si \(|\phi_1| < 1\), los efectos de un choque \(\varepsilon_t\) se van diluyendo en el tiempo.
Ejemplo: si \(\phi_1 = 0.7\), un shock de 10 se convierte en 7 el siguiente periodo, luego 4.9, luego 3.43, y así sucesivamente hasta desaparecer.
Si \(|\phi_1| = 1\), el efecto no se disipa: tenemos una raíz unitaria. Esto corresponde a un paseo aleatorio, que no es estacionario porque la varianza crece sin límite.
Si \(|\phi_1| > 1\), los efectos de un shock se amplifican con el tiempo y la serie explota, volviéndose inestable.
Generalización al AR(p)
En un modelo AR(p):
la condición de estabilidad se expresa en términos del polinomio característico:
donde \(L\) es el operador rezago.
Para que el modelo sea estable, todas las raíces de este polinomio deben estar fuera del círculo unitario, es decir, deben tener un módulo mayor que 1.
Dicho de otra forma: ningún valor de \(L\) dentro del círculo unitario (radio 1 en el plano complejo) debe anular la ecuación.
Intuición del círculo unitario
El círculo unitario es una forma matemática de decir:
Dentro del círculo (\(|\phi| < 1\)): el proceso es estable, los choques se disipan.
En el borde (\(|\phi| = 1\)): el proceso tiene raíz unitaria, no es estacionario (ejemplo típico: paseo aleatorio).
Fuera del círculo (\(|\phi| > 1\)): el proceso explota, los choques se amplifican con el tiempo.
El operador rezago (lag operator)#
El operador rezago se denota por \(L\) y simplemente significa “llevar la serie un paso hacia atrás”.
Por definición:
y de manera general:
Es decir, aplicar \(L\) una vez es ir un periodo atrás, aplicarlo \(k\) veces es ir \(k\) periodos atrás.
Ejemplo sencillo
Supongamos una serie \(y_t\) con valores:
En \(t=5\), \(y_5 = 10\)
Aplicamos \(L\): \(L y_5 = y_4\)
Aplicamos \(L^2\): \(L^2 y_5 = y_3\)
El operador rezago funciona como una “máquina del tiempo” que desplaza la serie hacia el pasado.
Usando el rezago en modelos AR
Un AR(1):
se puede escribir con el operador rezago como:
Reordenando:
Generalización al AR(p)
El modelo:
usando el operador rezago queda:
El polinomio característico
La parte entre paréntesis se llama polinomio característico:
La condición de estabilidad es que las raíces de :math:`Phi(L)` estén fuera del círculo unitario, es decir, que tengan módulo mayor que 1.
Esto garantiza que los choques \(\varepsilon_t\) no se acumulen sino que se disipen con el tiempo.
Intuición final
El operador \(L\) es solo una forma compacta de escribir “rezagos”.
Gracias a \(L\), podemos representar un modelo AR(p) como un polinomio.
Revisar las raíces del polinomio nos dice si la serie es estable (estacionaria) o si tiene una raíz unitaria (paseo aleatorio) o incluso si explota.
👉 Así, el operador rezago no es un “truco raro”, sino una herramienta matemática que simplifica la escritura y el análisis de modelos autorregresivos.
Cómo determinar el orden p en un modelo AR(p)#
Elegir el número de rezagos \(p\) es una de las decisiones más importantes en los modelos autorregresivos.
Existen tres enfoques principales: ACF/PACF, criterios de información y validación de residuales.
1. Análisis visual con ACF y PACF
ACF (Función de Autocorrelación):
Muestra cómo se correlaciona la serie con sus propios rezagos.
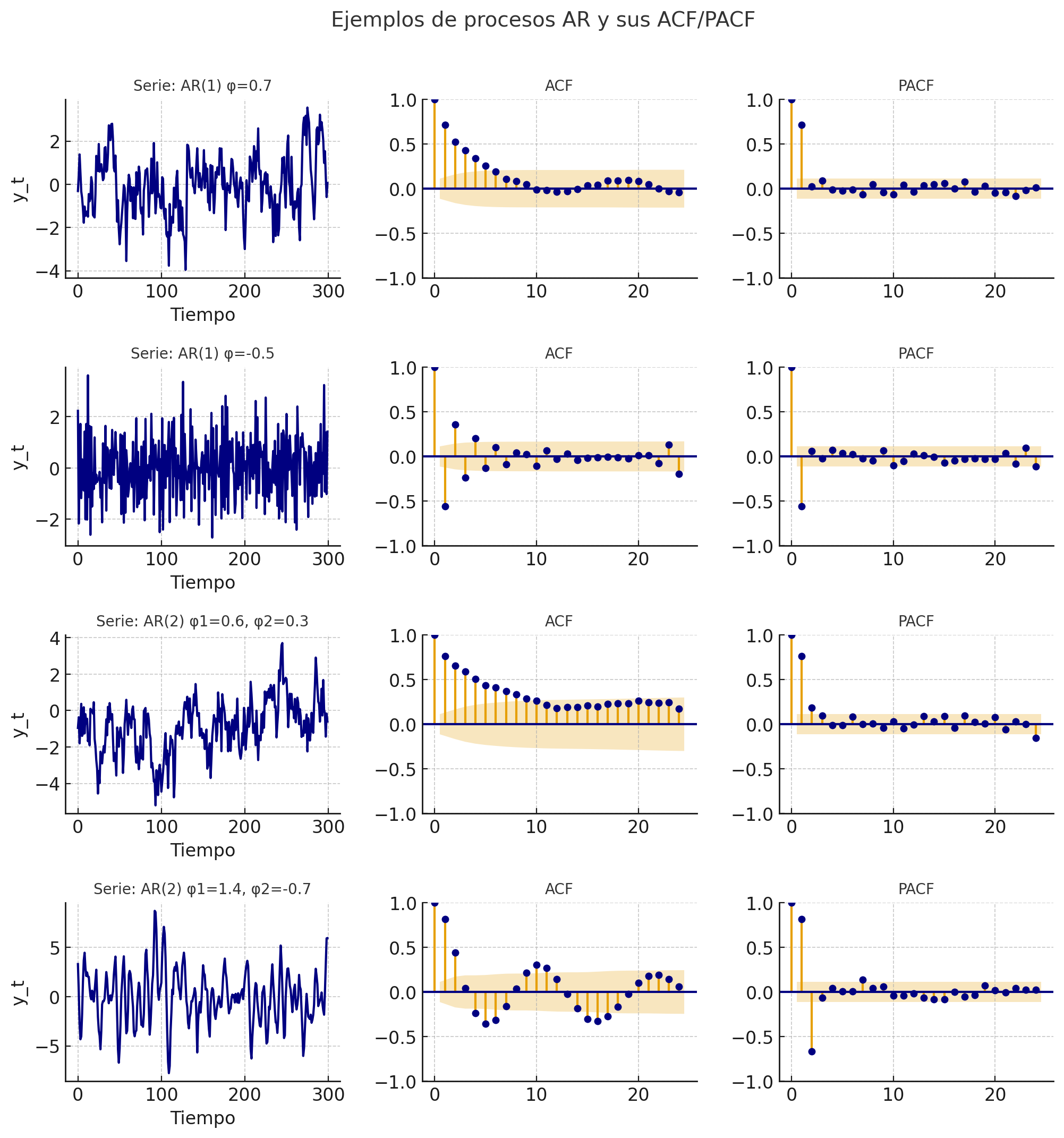
En un AR(p), la ACF no corta bruscamente; en cambio, decae de forma gradual (exponencial u oscilante). Un modelo AR(p) (autorregresivo) se caracteriza por tener una dependencia del pasado que se disipa gradualmente en el tiempo. Por eso, en teoría, la ACF de un proceso AR(p) no corta bruscamente, sino que decae suavemente (a veces de forma exponencial, a veces oscilando).
PACF (Función de Autocorrelación Parcial):
Mide la correlación entre \(y_t\) y \(y_{t-k}\) eliminando la influencia de los rezagos intermedios.
En un AR(p), la PACF muestra un corte brusco después del rezago \(p\).
Es decir: los primeros \(p\) rezagos aparecen significativos, y los demás son aproximadamente cero.
Ejemplo:
PACF con picos significativos en \(lag=1\) y \(lag=2\), pero no después → sugiere un AR(2).
ACF que decae lentamente confirma que el modelo es de tipo AR.
Cómo se comporta la ACF en diferentes casos:
Tipo de proceso |
Patrón en ACF |
Patrón en PACF |
|---|---|---|
AR(1) |
Decae exponencialmente u oscilando (según signo de φ₁) |
Corte brusco en lag 1 |
AR(2) |
Decaimiento suave u oscilante |
Corte en lag 2 |
MA(q) |
Corte brusco en lag q |
Decae lentamente |
ARMA(p,q) |
ACF y PACF decaen suavemente |
Ninguna corta bruscamente |
Ruido blanco |
Sin autocorrelación (todas ≈ 0) |
Sin autocorrelación (todas ≈ 0) |
Casos especiales donde la ACF no “decae lentamente”
Cuando los coeficientes AR son negativos:
La ACF oscila alrededor de cero (patrón de dientes de sierra) en lugar de decaer de manera monótona.
Ejemplo: AR(1) con φ₁ = –0.7 → alterna correlaciones positivas y negativas.
Cuando hay raíces complejas en un AR(2):
La ACF muestra ondas amortiguadas: un patrón oscilatorio que se atenúa con el tiempo.
No es “lento” en el sentido clásico, pero sigue siendo un decaimiento amortiguado.
Cuando el proceso no es estacionario:
Si \(|\phi| ≥ 1\), la ACF no decae (permanece alta o diverge).
Esto indica una raíz unitaria (paseo aleatorio), no un proceso AR estacionario.
2. Criterios de información (AIC, BIC)
Se ajustan modelos con distintos valores de \(p\) y se comparan criterios estadísticos:
AIC (Akaike Information Criterion)
BIC (Bayesian Information Criterion)
Regla: elegir el modelo que minimice estos valores.
El AIC suele preferir modelos más grandes (menos penalización).
El BIC es más estricto (prefiere modelos más simples).
Esto permite refinar la elección sugerida por ACF/PACF.
3. Validación de residuales
Después de elegir \(p\) con PACF o criterios de información:
Revisar los residuales del modelo: deben parecer ruido blanco.
ACF de residuales: no debe mostrar autocorrelación.
Prueba de Ljung–Box: no debe rechazar la hipótesis de independencia.
Si los residuales muestran autocorrelación → probablemente falten rezagos, aumentar \(p\).
Si el modelo parece sobreajustado (parámetros no significativos o \(p\) demasiado grande) → reducir \(p\).
4. Reglas empíricas adicionales
Series cortas (n < 50): conviene mantener \(p\) pequeño (ej. 1–3).
Series largas: se puede probar valores mayores de \(p\), pero un límite práctico es \(\sqrt{n}\) rezagos como máximo a evaluar.
Método |
Qué ob servar |
Patrón esperado en un AR(p) |
Cómo usarlo para elegir p |
|---|---|---|---|
ACF (Autocorrelación) |
Corre lación entre :math :y_t y r ezagos |
Decae lentamente (exponencial u oscilante), no corta bruscamente |
Confirma que la serie es de tipo AR |
PACF (Autocorrelación parcial) |
Corre lación d irecta entre :math :y_t y :ma th:y_ {t-k} elim inando r ezagos inter medios |
Corte brusco en el rezago p (los primeros p lags son significativos, luego ≈ 0) |
El último rezago significativo indica el valor de p |
Criterios de información (AIC, BIC) |
C alidad del ajuste pena lizada por compl ejidad |
Se comparan distintos modelos AR(p) |
Elegir el modelo con menor AIC/BIC; BIC suele ser más conservador |
Diagnóstico de residuales |
ACF y p ruebas estadí sticas sobre resi duales |
Residuales deben parecer ruido blanco |
Si hay autocorrelación → aumentar p; si hay sobreajuste → reducir p |
Reglas empíricas |
Lo ngitud de la serie :ma th:n |
p pequeño en series cortas; máximo práctico ≈ \(\sqrt{n}\) |
Limita el rango de búsqueda para p |
Ejemplos_AR#
Pronóstico con modelos AR#
El objetivo del pronóstico con un modelo autorregresivo AR(p) es estimar el valor futuro de la serie usando sus propios rezagos recientes. Partimos del modelo ajustado:
donde \(\varepsilon_t\) es ruido blanco.
1. Pronóstico a 1 paso adelante
El pronóstico en \(t+1\) dado lo observado hasta \(t\) es la esperanza condicional:
Es lineal en los últimos \(p\) valores observados.
Si el modelo incluye media \(\mu\) en vez de intercepto, puede escribirse como:
\[\hat y_{t+1\mid t} = \hat\mu + \hat\phi_1 (y_t-\hat\mu) + \cdots + \hat\phi_p (y_{t-p+1}-\hat\mu)\]
2. Pronóstico multi-paso (h pasos)
Para \(h \ge 2\) el pronóstico es recursivo: se sustituyen los valores futuros desconocidos por sus pronósticos previos.
Ejemplo AR(1):
En general:
Para AR(p), el mismo principio aplica pero usando la ecuación del modelo:
Para construir \(\hat y_{t+h\mid t}\) se usan \(y_{t},\dots,y_{t-p+1}\) y, cuando haga falta, \(\hat y_{t+1\mid t},\dots,\hat y_{t+h-1\mid t}\).
3. Incertidumbre del pronóstico e intervalos
La varianza del error de pronóstico crece con :math:`h` y se aproxima a la varianza incondicional del proceso cuando el modelo es estable.
Representación MA(\(\infty\)):
Varianza del error a \(h\) pasos:
Caso AR(1):
Intervalo de pronóstico aproximado al nivel \((1-\alpha)\):
4. Procedimiento práctico paso a paso
Preparación
Asegurar estacionariedad en media y varianza.
Remover tendencia y estacionalidad si existen (diferencias, desestacionalización, log).
Identificación de \(p\)
Leer ACF y PACF.
Comparar AIC y BIC en varios AR(p).
Estimación
Ajustar el AR(p) por mínimos cuadrados o máxima verosimilitud.
Verificar estabilidad (raíces fuera del círculo unitario).
Diagnóstico
Residuales ~ ruido blanco (ACF/PACF de residuales, Ljung–Box).
Q–Q plot si se requiere normalidad para inferencia.
Pronóstico
Generar \(\hat y_{t+h\mid t}\) de forma recursiva.
Calcular intervalos de pronóstico con la varianza correspondiente.
Evaluación fuera de muestra
Backtesting con ventana rodante o expansiva.
Métricas: MAE, RMSE, MAPE, MSE.
Comparar con benchmarks simples: promedio, naïve, random walk, SES.
5. Intuiciones útiles
A medida que \(h\) aumenta, el pronóstico converge a la media del proceso estacionario.
Un \(\phi\) cercano a 1 implica persistencia alta y, por tanto, intervalos más anchos para horizontes largos.
En AR(2) con raíces complejas, los pronósticos presentan oscilaciones amortiguadas hacia la media.
Si hay autocorrelación remanente en residuales, el modelo tiende a subestimar la incertidumbre del pronóstico.
Pronóstico in-sample y out-of-sample#
Cuando ajustamos un modelo AR(p), podemos evaluar su capacidad de pronóstico de dos formas distintas:
in-sample (dentro de la muestra) y out-of-sample (fuera de la muestra).
1. Pronóstico in-sample (dentro de la muestra)
Corresponde a los valores ya observados que el modelo intenta reconstruir o explicar dentro del periodo usado para entrenar el modelo.
Se calculan los valores ajustados usando los mismos datos del entrenamiento.
Permiten evaluar qué tan bien el modelo reproduce la dinámica del pasado.
Propósito:
Evaluar el ajuste interno del modelo (goodness of fit).
Indicadores comunes:
\(R^2\) o coeficiente de determinación.
Error medio cuadrático (MSE) o raíz del error cuadrático medio (RMSE).
Análisis visual: comparación entre serie observada y serie ajustada.
Limitación:
Un modelo puede tener un ajuste excelente in-sample y, aun así, fallar al predecir el futuro → riesgo de sobreajuste (overfitting).
2. Pronóstico out-of-sample (fuera de la muestra)
Corresponde a valores futuros no usados en la estimación del modelo.
Se usa para evaluar la capacidad predictiva real.
Se realiza sobre un conjunto de prueba (test) separado del entrenamiento.
Los valores pasados de \(y_t\) pueden provenir de datos reales o de pronósticos previos (pronóstico recursivo).
Mide qué tan bien el modelo generaliza a datos nuevos.
Propósito:
Evaluar la capacidad de pronóstico genuina, no el ajuste histórico.
Métricas comunes:
RMSE (Root Mean Squared Error)
MSE (Mean Squared Error)
MAE (Mean Absolute Error)
MAPE (Error porcentual absoluto medio)
3. Ejemplo conceptual
Suponemos que tenemos una serie de 120 meses.
Período |
Uso |
Descripción |
|---|---|---|
Mes 1 – 100 |
Entrenamiento |
Se usa para estimar el modelo (in-sample) |
Mes 101 – 120 |
Prueba |
Se usa para evaluar pronóstico futuro (out-of-sample) |
Ajustas el modelo AR(p) con los primeros 100 meses.
Calculas los valores ajustados \(\hat y_t\) → in-sample.
Realizas pronósticos recursivos para los meses 101 a 120 → out-of-sample.
Comparas con los valores reales \(y_{101}, \dots, y_{120}\).
4. Evaluación conjunta
Tipo de pronóstico |
Datos usados |
Propósito |
Riesgos |
Métricas |
|---|---|---|---|---|
In-sample |
Datos de e ntrenamiento |
Verificar ajuste interno |
Sobr eajuste (modelo de masiado co mplejo) |
R², MSE, RMSE, MAE, MAPE |
Out-of-sample |
Datos de prueba (no vistos) |
Evaluar capacidad p redictiva real |
V arianza alta o mala general ización |
R², MSE, RMSE, MAE, MAPE |
5. Buenas prácticas
Siempre separar los datos en entrenamiento y prueba (por ejemplo, 80/20).
Validar con pronóstico recursivo.
Un modelo útil no es el que mejor ajusta el pasado, sino el que predice mejor el futuro.
Comparar los errores out-of-sample con un modelo naïve (por ejemplo, \(y_{t+1} = y_t\)).
Si el AR(p) no mejora al modelo naïve → no agrega valor predictivo.
6. Visualización típica
Gráfico de la serie observada, con:
Datos reales (entrenamiento + prueba).
Pronóstico in-sample (ajuste).
Pronóstico out-of-sample (proyección futura).
Intervalo de confianza.
7. Conclusión
In-sample: mide qué tan bien el modelo explica el pasado.
Out-of-sample: mide qué tan bien el modelo predice el futuro.
Ambos deben analizarse juntos:
Buen ajuste in-sample + mal desempeño out-of-sample → sobreajuste.
Mal ajuste in-sample + buen desempeño out-of-sample → modelo más robusto.
En series de tiempo, el verdadero test de un modelo AR no es qué tan bien ajusta la historia, sino qué tan creíblemente anticipa lo que aún no ha ocurrido.
¿Intercepto o media en un modelo AR(p)?#
1. Forma con intercepto Un modelo AR(p) puede escribirse como:
Aquí, \(\alpha\) es el intercepto.
Esta forma es útil cuando se está estimando directamente por regresión (ej. mínimos cuadrados) porque se trata como una constante más.
2. Forma centrada en la media
donde \(\mu\) es la media de la serie.
En este caso no se incluye \(\alpha\) explícitamente, porque ya está absorbida en la media.
3. Relación entre intercepto y media
Si trabajas con intercepto:
Siempre que \(1 - \phi_1 - \cdots - \phi_p \neq 0\) (condición de estacionariedad).
4. ¿Cuándo usar cada forma?
Intercepto (\(\alpha\)):
Cuando el modelo se estima con métodos de regresión lineal directamente.
Es la forma más común en la práctica computacional.
Los paquetes de software (
statsmodels,R, etc.) suelen reportar \(\alpha\).
Media (\(\mu\)):
Cuando quieres interpretar el modelo en términos de la tendencia de largo plazo.
Útil para entender hacia dónde converge el pronóstico cuando el horizonte \(h \to \infty\) (siempre converge a \(\mu\)).
En textos teóricos se usa porque facilita derivar propiedades (media, varianza, covarianza).
5. Intuición
El intercepto \(\alpha\) es una “constante de ajuste” en la ecuación de regresión.
La media \(\mu\) es el “punto de equilibrio” del proceso: el valor al que los pronósticos tienden con el tiempo.
Estimación de parámetros en un modelo AR(p)#
Existen tres métodos principales para estimar los parámetros \(\alpha, \phi_1, \dots, \phi_p\).
1. Estimación por Mínimos Cuadrados (OLS)
Se reescribe el AR(p) como una regresión lineal múltiple:
Se estima minimizando la suma de cuadrados de los residuos:
Es equivalente a un modelo de regresión estándar con \(y_t\) como variable dependiente y sus rezagos como explicativas.
Ventajas:
Sencillo y directo.
Bien implementado en cualquier software estadístico.
Consistente y eficiente si \(\varepsilon_t\) es ruido blanco gaussiano.
Limitación:
Puede no ser tan eficiente si los residuos no son normales.
2. Estimación por Máxima Verosimilitud (MLE)
Asume que \(\varepsilon_t \sim N(0,\sigma_\varepsilon^2)\).
La función de verosimilitud es el producto de las densidades normales de los residuos.
En práctica, se trabaja con la log-verosimilitud:
Maximizar \(\ell(\theta)\) es equivalente a minimizar la suma de cuadrados de los residuos si se asume normalidad.
Por eso, en un AR puro, el MLE y OLS producen estimadores muy similares.
Ventajas:
Permite construir intervalos de confianza y pruebas de hipótesis bajo supuestos normales.
Es la base para comparar modelos usando AIC/BIC.
Limitación:
Requiere normalidad de los errores para ser eficiente.
3. Estimación por Yule–Walker
Se basa en las ecuaciones de autocorrelación del proceso AR(p):
Estas forman un sistema lineal que relaciona los coeficientes \(\phi_i\) con las autocorrelaciones muestrales \(\hat\rho_k\).
Resolviendo el sistema se obtienen los estimadores de Yule–Walker.
Ventajas:
Fácil de calcular.
Útil como estimador inicial para otros métodos (ej. en algoritmos iterativos).
Rápido computacionalmente.
Limitación:
Puede ser menos eficiente que OLS/MLE en muestras pequeñas.
Depende fuertemente de la calidad de las estimaciones de autocorrelación.
Comparación de los métodos
Método |
Supuestos clave |
Ventajas principales |
Lim itaciones |
|---|---|---|---|
OLS |
Errores no correlacionados |
Sencillo, intuitivo |
Menos eficiente si no hay n ormalidad |
MLE |
Errores normales iid |
Permite inferencia estadística (intervalos, tests) y selección por AIC/BIC |
Computaci onalmente más exigente |
** Yule–Walker** |
Estacionariedad |
Rápido, útil para inicialización |
Menos eficiente en muestras pequeñas |
Evaluación de la significancia de los parámetros en un modelo AR(p)#
Una vez estimado el modelo:
cada parámetro \(\phi_i\) y el intercepto \(\alpha\) tienen un estimador \(\hat\phi_i\) y un error estándar \(SE(\hat\phi_i)\).
1. Prueba t individual
La forma más común de evaluar la significancia de cada parámetro es mediante la prueba z:
Hipótesis:
\(H_0\): \(\phi_i = 0\) (el rezago \(i\) no tiene efecto significativo)
\(H_1\): \(\phi_i \neq 0\) (el rezago sí tiene efecto)
Criterio de decisión:
Si \(|z_i| > z_{\text{crítico}}\) o el valor p < 0,05 → se rechaza \(H_0\).
Es decir, el coeficiente \(\phi_i\) es significativo.
Como referencia:
Si \(|z| > 1.96\) → significativo al 5%
Si \(|z| > 2.58\) → significativo al 1%
Interpretación:
Un parámetro significativo indica que ese rezago aporta información predictiva sobre \(y_t\).
Un parámetro no significativo puede eliminarse para simplificar el modelo.
2. Error estándar y significancia práctica
Aunque un coeficiente sea estadísticamente significativo (valor p < 0.05), también se evalúa su magnitud:
Si \(\phi_i\) es muy pequeño, su influencia práctica puede ser mínima.
En modelos con muchos rezagos, eliminar coeficientes pequeños y no significativos mejora la parsimonia.
3. Prueba conjunta (Wald o F)
También se puede evaluar si varios parámetros a la vez son iguales a cero:
Esto se puede hacer con una prueba F (en OLS) o Wald test (en MLE).
Si se rechaza \(H_0\), el conjunto de rezagos aporta información significativa al modelo.
4. Valores p y tabla resumen
Los paquetes estadísticos (por ejemplo, statsmodels en Python)
entregan una tabla con:
Parámetro |
Coeficiente |
Error estándar |
Valor t |
Valor p |
Significancia |
|---|---|---|---|---|---|
\(\alpha\) |
0.502 |
0.091 |
5.49 |
0.000 |
*** |
\(\phi_1\) |
0.634 |
0.084 |
7.56 |
0.000 |
*** |
\(\phi_2\) |
-0.213 |
0.092 |
-2.31 |
0.022 |
** |
… |
… |
… |
… |
… |
… |
Los asteriscos indican niveles de significancia:
***p < 0.01 (muy significativo)**p < 0.05 (significativo)*p < 0.10 (marginal)nsno significativo
5. Cuándo preocuparse por la significancia
Si muchos coeficientes no son significativos → probablemente \(p\) es demasiado grande (sobreajuste).
Si todos son significativos → el modelo capta bien la dinámica.
Si solo los primeros rezagos son significativos → se puede reducir el orden a ese nivel.
6. Precaución: correlación entre rezagos
En modelos con rezagos cercanos (por ejemplo, AR(6)), puede existir colinealidad entre los valores pasados.
Esto aumenta los errores estándar y puede hacer que algunos coeficientes no parezcan significativos, aunque el modelo global sí lo sea.
Por eso también se usa el AIC/BIC y el diagnóstico de residuales para validar el modelo completo, no solo los valores p individuales.
7. Resumen práctico
Paso |
Qué se evalúa |
Herramienta |
Interpretación |
|---|---|---|---|
1 |
Significancia individual de \(\phi_i\) |
Prueba t, valor p |
Si p < 0.05, el rezago es relevante |
2 |
Significancia conjunta de varios \(\phi_i\) |
Prueba F o Wald |
Evalúa si los rezagos en conjunto explican la serie |
3 |
Parsimonia del modelo |
AIC/BIC y residuos |
Confirmar que no hay sobreajuste |
4 |
Multicolinealidad |
Revisar correlaciones entre rezagos |
Si alta, puede afectar las t |
Intervalos de confianza en los modelos AR#
Cuando ajustamos un modelo autorregresivo con statsmodels, en la
tabla de resultados aparecen dos columnas adicionales Las columnas
[0.025, 0.975] representan los límites inferior y superior del
intervalo de confianza al 95% para cada parámetro estimado.
1. ¿Qué es un intervalo de confianza?
Un intervalo de confianza (IC) indica el rango de valores dentro del cual se espera que se encuentre el valor real del parámetro poblacional, con una probabilidad determinada (habitualmente 95%).
Formalmente, para cada parámetro \(\hat{\phi_i}\):
donde:
\(\hat{\phi_i}\) → coeficiente estimado,
\(SE(\hat{\phi_i})\) → error estándar del coeficiente,
\(1.96\) → valor crítico de la distribución normal estándar para un 95% de confianza.
2. Interpretación práctica
El intervalo [0.025, 0.975] muestra el rango en el que se encuentra el valor verdadero del parámetro con 95% de confianza.
Si el intervalo no contiene el valor 0, se concluye que el parámetro es estadísticamente significativo.
Si el intervalo incluye 0, no se puede afirmar que el efecto sea distinto de cero.
3. Interpretación geométrica
El punto central del intervalo es el coeficiente estimado.
El ancho del intervalo depende del error estándar:
Intervalo estrecho → estimación precisa.
Intervalo ancho → estimación incierta (poca información en los datos).