Taller N° 1: VaR método Delta-Normal o varianzas-covarianzas#
Portafolio de inversión conformado por las siguientes acciones:
Facebook, Inc. (FB).
The Coca-Cola Company (KO).
Kellogg Company (K).
Ford Motor Company (F).
McDonald’s Corporation (MCD).
Utilizar una base de datos de precios diarios desde primero de abril de 2018 hasta el 21 de abril de 2020.
Importar datos desde Yahoo Finance.#
library(quantmod)
library(tseries)
La fecha final debe ser el 22 de abril de 2020 para que descargue hasta el 21 de abril de 2020.
FB = get.hist.quote(instrument = "FB", start = as.Date("2018-04-01"), end = as.Date("2020-04-22"), quote = "AdjClose")
time series starts 2018-04-02
time series ends 2020-04-21
KO = get.hist.quote(instrument = "KO", start = as.Date("2018-04-01"), end = as.Date("2020-04-22"), quote = "AdjClose")
time series starts 2018-04-02
time series ends 2020-04-21
K = get.hist.quote(instrument = "K", start = as.Date("2018-04-01"), end = as.Date("2020-04-22"), quote = "AdjClose")
time series starts 2018-04-02
time series ends 2020-04-21
F = get.hist.quote(instrument = "F", start = as.Date("2018-04-01"), end = as.Date("2020-04-22"), quote = "AdjClose")
time series starts 2018-04-02
time series ends 2020-04-21
MCD = get.hist.quote(instrument = "MCD", start = as.Date("2018-04-01"), end = as.Date("2020-04-22"), quote = "AdjClose")
time series starts 2018-04-02
time series ends 2020-04-21
Matriz de precios.#
precios = merge(FB, KO, K, F, MCD)
precios = ts(precios)
print(head(precios))
Adjusted.FB Adjusted.KO Adjusted.K Adjusted.F Adjusted.MCD
[1,] 155.39 39.61916 58.16813 9.572072 149.2148
[2,] 156.11 40.27839 58.39851 9.827681 151.7503
[3,] 155.10 41.07690 59.83614 9.986334 153.0085
[4,] 159.34 41.22546 59.49516 10.003963 155.1088
[5,] 157.20 40.77978 59.20026 9.854123 152.5544
[6,] 157.93 40.69621 59.42144 9.915821 152.5355
dim(precios)
- 518
- 5
Se cargaron cinco acciones cada una con 518 precios.
Número de acciones.#
acciones = ncol(precios)
acciones
Matriz de rendimientos.#
rendimientos = diff(log(precios))
dim(rendimientos)
- 517
- 5
Hay 517 rendimientos por acción.
\(S_0:\)Precio actual de cada acción.#
s = tail(precios,1)
s = as.numeric(s)
s
- 170.800003
- 44.971439
- 64.949127
- 4.77
- 176.403854
Número de acciones del portafolio de inversión.#
numero_acciones = c(2000, 5000, 2000, 10000, 1000)
numero_acciones
- 2000
- 5000
- 2000
- 10000
- 1000
Valor de mercado de cada acción.#
valor_mercado_acciones = numero_acciones*s
valor_mercado_acciones
- 341600.006
- 224857.195
- 129898.254
- 47700
- 176403.854
Valor de mercado del portafolio de inversión.#
valor_portafolio = sum(valor_mercado_acciones)
valor_portafolio
Proporciones de inversión.#
proporciones = valor_mercado_acciones/valor_portafolio
proporciones
- 0.371119073553745
- 0.244288034029758
- 0.141123298694348
- 0.0518219540327339
- 0.191647639689415
sum(proporciones)
\(\mu:\) Rendimiento esperado de cada acción.#
rendimientos_esperados = apply(rendimientos,2,mean)
print(rendimientos_esperados)
Adjusted.FB Adjusted.KO Adjusted.K Adjusted.F Adjusted.MCD
0.0001828921 0.0002450962 0.0002132818 -0.0013472019 0.0003237701
\(\sigma:\)Volatilidad de cada acción.#
volatilidades = apply(rendimientos,2,sd)
print(volatilidades)
Adjusted.FB Adjusted.KO Adjusted.K Adjusted.F Adjusted.MCD
0.02415253 0.01563877 0.01749543 0.02410755 0.01889120
Matriz varianzas-covarianzas.#
covarianzas = cov(rendimientos)
print(covarianzas)
Adjusted.FB Adjusted.KO Adjusted.K Adjusted.F Adjusted.MCD
Adjusted.FB 5.833447e-04 0.0001283637 6.003732e-05 2.767284e-04 2.073812e-04
Adjusted.KO 1.283637e-04 0.0002445710 1.304011e-04 1.783455e-04 1.617992e-04
Adjusted.K 6.003732e-05 0.0001304011 3.060901e-04 9.705185e-05 8.338021e-05
Adjusted.F 2.767284e-04 0.0001783455 9.705185e-05 5.811738e-04 2.592786e-04
Adjusted.MCD 2.073812e-04 0.0001617992 8.338021e-05 2.592786e-04 3.568773e-04
Coeficientes de correlación.#
correlaciones = cor(rendimientos)
print(correlaciones)
Adjusted.FB Adjusted.KO Adjusted.K Adjusted.F Adjusted.MCD
Adjusted.FB 1.0000000 0.3398420 0.1420804 0.4752675 0.4545139
Adjusted.KO 0.3398420 1.0000000 0.4766003 0.4730496 0.5476644
Adjusted.K 0.1420804 0.4766003 1.0000000 0.2301051 0.2522777
Adjusted.F 0.4752675 0.4730496 0.2301051 1.0000000 0.5693170
Adjusted.MCD 0.4545139 0.5476644 0.2522777 0.5693170 1.0000000
Rendimientos del portafolio de inversión.#
rendimientos_portafolio=vector()
for(i in 1:nrow(rendimientos)){
rendimientos_portafolio[i] = sum(rendimientos[i,]*proporciones)
}
Rendimiento esperado del portafolio de inversión#
rendimiento_esperado_portafolio = mean(rendimientos_portafolio)
rendimiento_esperado_portafolio
Volatilidad del portafolio de inversión#
volatilidad_portafolio = sd(rendimientos_portafolio)
volatilidad_portafolio
Volatilidad del portafolio a partir de la matriz de varianzas-covarianzas#
volatilidad_portafolio = sqrt(sum(t(proporciones)%*%covarianzas*proporciones))
volatilidad_portafolio
Preguntas#
Una semana tiene 5 días bursátiles.
Un mes tiene 20 días bursátiles.
Un año tiene 250 días bursátiles.
Un mes tiene 4 semanas.
Un año tiene 52 semanas.
1. Con un nivel de confianza del 95%, ¿Cuál es el VaR (sin promedios) semanal de la acción de FB en términos monetarios?#
NC = 0.95
t = 5
VaR_individuales_sin_promedios = valor_mercado_acciones*volatilidades*qnorm(NC)*sqrt(t)
VaR_individuales_sin_promedios[1]
2. Con un nivel de confianza del 95%, ¿Cuál es el VaR (sin promedios) semanal de la acción de F en términos monetarios?#
NC = 0.95
t = 5
VaR_individuales_sin_promedios = valor_mercado_acciones*volatilidades*qnorm(NC)*sqrt(t)
VaR_individuales_sin_promedios[4]
3. Con un nivel de confianza del 99%, ¿Cuál es el VaR (sin promedios) semanal de la acción de MCD en términos monetarios?#
NC = 0.99
t = 5
VaR_individuales_sin_promedios = valor_mercado_acciones*volatilidades*qnorm(NC)*sqrt(t)
VaR_individuales_sin_promedios[5]
4. Con un nivel de confianza del 99%, ¿Cuál es el VaR (sin promedios) semanal de la acción de K en términos monetarios?#
NC = 0.99
t = 5
VaR_individuales_sin_promedios = valor_mercado_acciones*volatilidades*qnorm(NC)*sqrt(t)
VaR_individuales_sin_promedios[3]
5. Con un nivel de confianza del 99%, ¿Cuál es el VaR (sin promedios) semanal del portafolio de inversión en términos monetarios?#
NC = 0.99
t = 5
VaR_portafolio_sin_promedios = sqrt(sum(t(VaR_individuales_sin_promedios)%*%correlaciones*VaR_individuales_sin_promedios))
VaR_portafolio_sin_promedios
6. Con un nivel de confianza del 99%, ¿Cuál es el VaR (sin promedios) diario de la acción F en términos monetarios?#
NC = 0.99
t = 1
VaR_individuales_sin_promedios = valor_mercado_acciones*volatilidades*qnorm(NC)*sqrt(t)
VaR_individuales_sin_promedios[1]
7. Con un nivel de confianza del 99%, ¿Cuál es el VaR (sin promedios) diario de la acción KO en términos monetarios?#
NC = 0.99
t = 1
VaR_individuales_sin_promedios = valor_mercado_acciones*volatilidades*qnorm(NC)*sqrt(t)
VaR_individuales_sin_promedios[2]
8. Con un nivel de confianza del 97,5%, ¿Cuál es el VaR (sin promedios) diario del portafolio de inversión en términos monetarios?#
NC = 0.975
t = 1
VaR_portafolio_sin_promedios = sqrt(sum(t(VaR_individuales_sin_promedios)%*%correlaciones*VaR_individuales_sin_promedios))
VaR_portafolio_sin_promedios
9. Con un nivel de confianza del 99%, ¿Cuál es el VaR (con promedios) semanal de la acción KO en términos monetarios?#
NC = 0.99
t = 5
VaR_individuales_con_promedios = valor_mercado_acciones*abs(rendimientos_esperados*t+qnorm(1-NC,sd=volatilidades*sqrt(t)))
VaR_individuales_con_promedios[2]
10. Con un nivel de confianza del 95%, ¿Cuál es el VaR (con promedios) mensual de la acción F en términos monetarios?#
NC = 0.95
t = 20
VaR_individuales_con_promedios = valor_mercado_acciones*abs(rendimientos_esperados*t+qnorm(1-NC,sd=volatilidades*sqrt(t)))
VaR_individuales_con_promedios[4]
11. Con un nivel de confianza del 99%, ¿Cuál es el VaR (con promedios) mensual del portafolio de inversión en términos monetarios?#
NC = 0.99
t = 20
VaR_portafolio_con_promedios = sqrt(sum(t(VaR_individuales_con_promedios)%*%correlaciones*VaR_individuales_con_promedios))
VaR_portafolio_con_promedios
12. Con un nivel de confianza del 98%, ¿Cuál es el VaR (con promedios) mensual del portafolio de inversión en términos monetarios?#
NC = 0.98
t = 20
VaR_portafolio_con_promedios = sqrt(sum(t(VaR_individuales_con_promedios)%*%correlaciones*VaR_individuales_con_promedios))
VaR_portafolio_con_promedios
13. Con un nivel de confianza del 99%, ¿Cuál es el Beneficios por Diversificación (BD) diario del portafolio de inversión en términos monetarios?#
Nota: usar el método de VaR (sin promedios).
NC = 0.99
t = 1
VaR_individuales_sin_promedios = valor_mercado_acciones*volatilidades*qnorm(NC)*sqrt(t)
VaR_portafolio_sin_promedios = sqrt(sum(t(VaR_individuales_sin_promedios)%*%correlaciones*VaR_individuales_sin_promedios))
suma_VaR_individuales_sin_promedios = sum(VaR_individuales_sin_promedios)
BD_sin_promedios=suma_VaR_individuales_sin_promedios-VaR_portafolio_sin_promedios
BD_sin_promedios
14. Con un nivel de confianza del 99%, ¿Cuál es el Beneficios por Diversificación (BD) diario del portafolio de inversión en términos monetarios?#
Nota: usar el método de VaR (con promedios).
NC = 0.99
t = 1
VaR_individuales_con_promedios = valor_mercado_acciones*abs(rendimientos_esperados*t+qnorm(1-NC,sd=volatilidades*sqrt(t)))
VaR_portafolio_con_promedios = sqrt(sum(t(VaR_individuales_con_promedios)%*%correlaciones*VaR_individuales_con_promedios))
suma_VaR_individuales_con_promedios = sum(VaR_individuales_con_promedios)
BD_con_promedios = suma_VaR_individuales_con_promedios-VaR_portafolio_con_promedios
BD_con_promedios
Gráficos#
Precios de las acciones.#
plot(precios, col = "darkblue", lwd = 2, xlab = "Tiempo", main = "Precios")
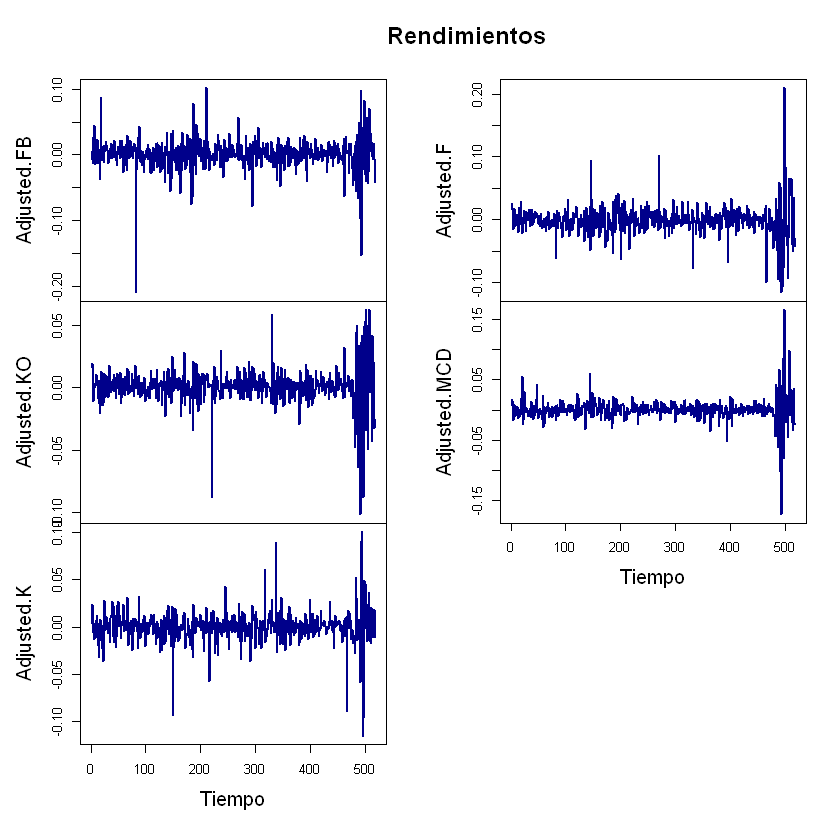
Rendimientos de las acciones.#
plot(rendimientos, col = "darkblue", lwd = 2, xlab = "Tiempo", main = "Rendimientos")