Volatilidad EWMA#

Importar datos#

datos = read.csv("Tres acciones.csv", sep=";", dec=",", header = T)

Matriz de precios#

precios = datos[,-1]

nombres = colnames(precios)
nombres
  1. 'ECO'
  2. 'PFBCOLOM'
  3. 'ISA'
acciones = ncol(precios)
acciones
3
precios = ts(precios)

Matriz de rendimientos#

rendimientos = diff(log(precios))

Gráfico de los rendimientos#

plot(rendimientos, main = "Rendimientos")
../../../_images/output_11_010.png

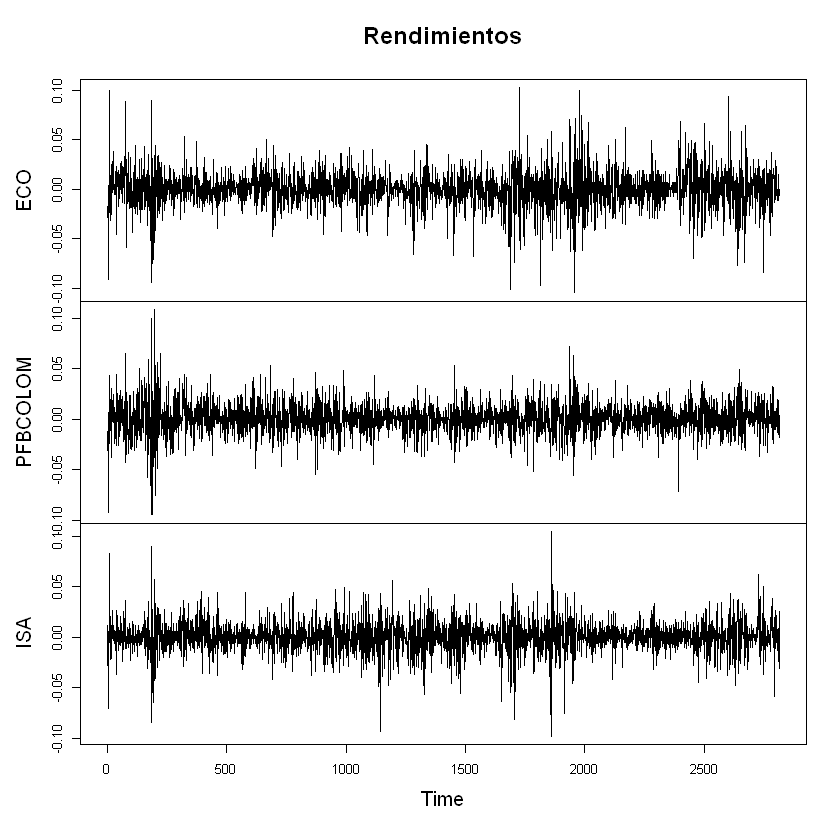
Volatilidad de cada acción#

Esta forma de calcular la volatilidad también se llama volatilidad histórica. Cada uno de los rendimientos tiene igual peso para la volatilidad.

volatilidades = apply(rendimientos, 2, sd)
print(volatilidades)

       ECO   PFBCOLOM        ISA
0.01862871 0.01583774 0.01556859

Volatilidad EWMA#

Varianza:

\[\sigma^2_t = \lambda \sigma^2_{t-1}+(1-\lambda)r^2_{t-1}\]

Volatilidad EWMA:

\[\sigma_t = \sqrt{\lambda \sigma^2_{t-1}+(1-\lambda)r^2_{t-1}}\]

\(\sigma_t:\) volatilidad en el período t.

\(\sigma^2_{t-1}:\) varianza del período \(t - 1\).

\(r^2_{t-1}:\) cuadrado de la rentabilidad del período \(t - 1\).

\(\lambda:\) Factor de decaimiento (decay factor). Es una constante y \(0 < \lambda < 1\). También llamada constante de suavizado.

Lambda determina los pesos que se aplican a las observaciones y la cantidad efectiva de datos que se utilizarán. Mientras más pequeño sea lambda, mayor peso tienen los datos recientes.

1

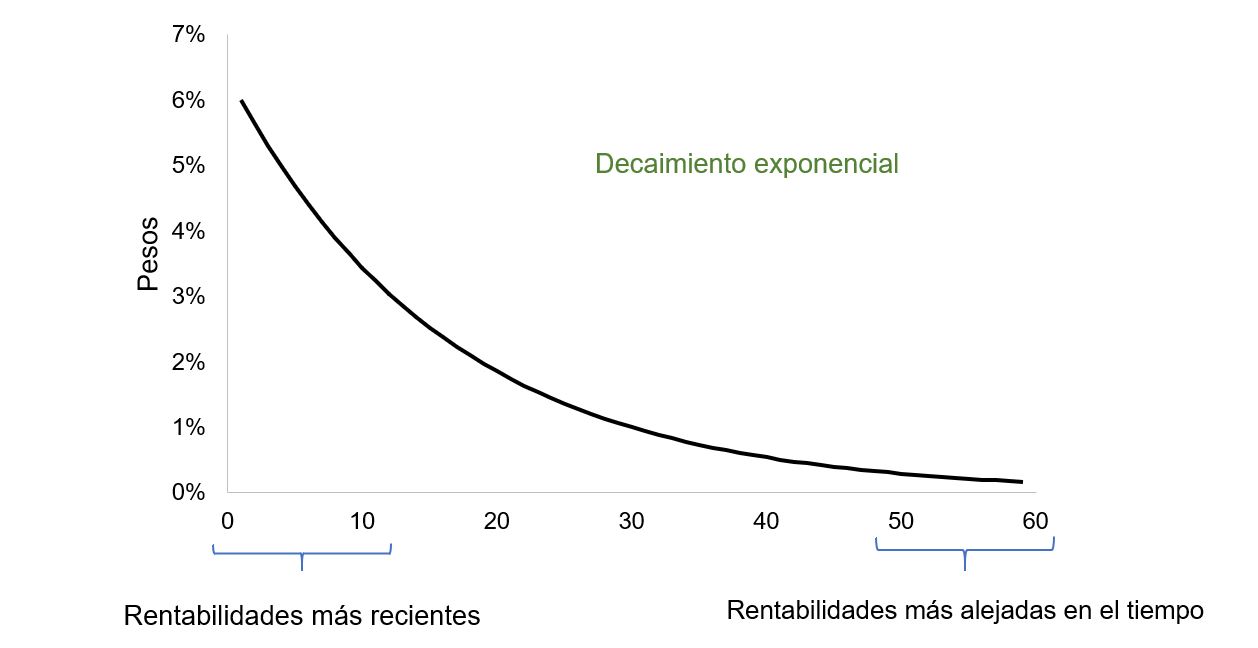
1#

Recomendaciones de J. P. Morgan: Riskmetrics

  • \(\lambda = 0,94\) para rendimientos diarios.

  • \(\lambda = 0,97\) para rendimientos mensuales.

numero_rendimientos = nrow(rendimientos)
numero_rendimientos
2815

Se utilizará lambda igual a 0.94. Este valor es recomendado para frecuencias diarias.

lambda = 0.94

Se calculará la volatilidad EWMA para cada período por cada acción. El primer período tendra un valor igual a cero. Por tanto, en el segundo ciclo for se empezará a partir de la segunda fila, porque en la primera se especificará que será igual a cero.

volatilidad_EWMA = matrix(, numero_rendimientos, acciones) # Matriz para calcular volatilidad EWMA para cada período por acción.

volatilidad_EWMA[1,] = 0 # La primera fila de la matriz anterior tendrá como valor semilla igual a cero.

for(j in 1:acciones){

    for(i in 2:numero_rendimientos){

        volatilidad_EWMA[i, j] = sqrt((1 - lambda)*rendimientos[i - 1, j]^2 + lambda*volatilidad_EWMA[i - 1, j]^2)

}
}

En el código anterior, debido a que la volatilidad EWMA es recursiva, la volatilidad del período actual depende del rendimiento y de la volatilidad EWMA del período anterior \(t - 1\). Por esto, se utiliza [i - 1] para indicar que se utiliza el valor del período anterior.

print(head(volatilidad_EWMA))
print(tail(volatilidad_EWMA))

            [,1]        [,2]        [,3]
[1,] 0.000000000 0.000000000 0.000000000
[2,] 0.004335493 0.006201571 0.006740513
[3,] 0.008140972 0.009685775 0.007133887
[4,] 0.009827886 0.009515765 0.009480782
[5,] 0.017128395 0.009307423 0.010199546
[6,] 0.017135220 0.012592325 0.014240597
              [,1]       [,2]       [,3]
[2810,] 0.01467410 0.01202480 0.01661564
[2811,] 0.01431925 0.01191950 0.01623989
[2812,] 0.01393615 0.01239107 0.01587858
[2813,] 0.01356672 0.01277761 0.01549780
[2814,] 0.01315342 0.01238892 0.01627948
[2815,] 0.01285754 0.01204027 0.01749096

Volatilidad EWMA de cada acción#

El último valor corresponde a la volatilidad EWMA de cada acción.

vol_EWMA = tail(volatilidad_EWMA, 1)
print(vol_EWMA)

              [,1]       [,2]       [,3]
[2815,] 0.01285754 0.01204027 0.01749096

colnames(vol_EWMA) = nombres # se renombran las columnas con los nombres de las acciones.
print(vol_EWMA)

               ECO   PFBCOLOM        ISA
[2815,] 0.01285754 0.01204027 0.01749096

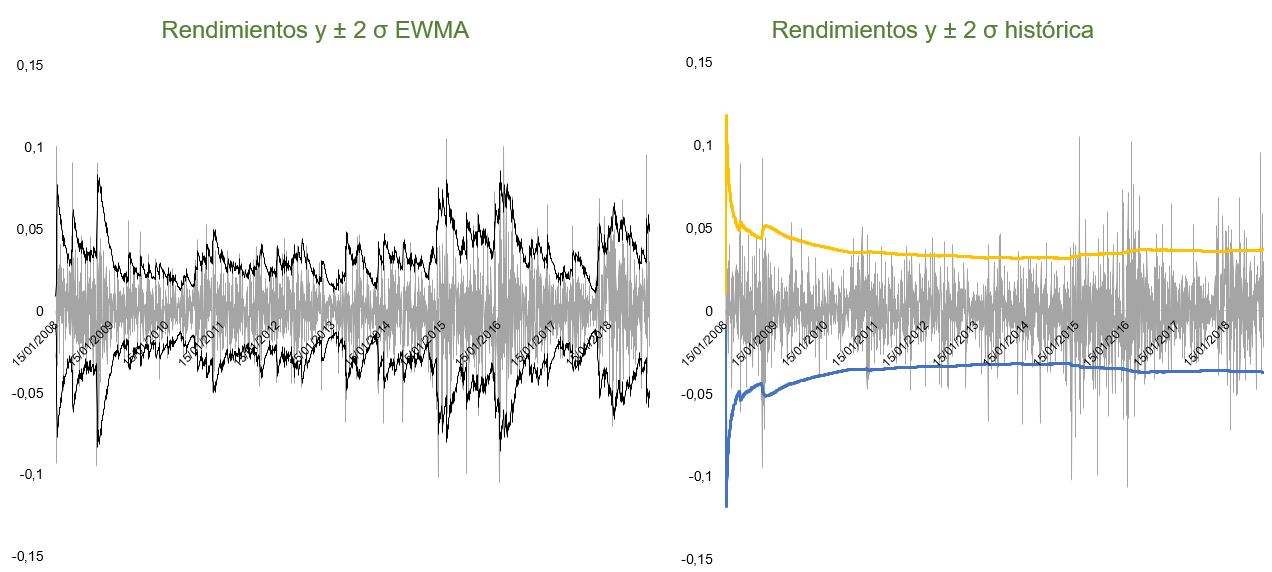
Volatilidad EWMA:

  • ECO: 1,29% diaria.

  • PFBCOLOM: 1,20% diaria.

  • ISA: 1,75% diaria.

Volatilidad histórica de cada acción#

Anteriormente se habían calculado.

print(volatilidades)

       ECO   PFBCOLOM        ISA
0.01862871 0.01583774 0.01556859

Volatilidad histórica:

  • ECO: 1,86% diaria.

  • PFBCOLOM: 1,84% diaria.

  • ISA: 1,56% diaria.

2

2#