Métricas para Evaluación de Modelos de Clasificación#
Cuando entrenamos un modelo de clasificación, no basta con ver si “acierta” o “falla”.
Necesitamos métricas que nos digan qué tan bueno es el modelo y en qué se equivoca.
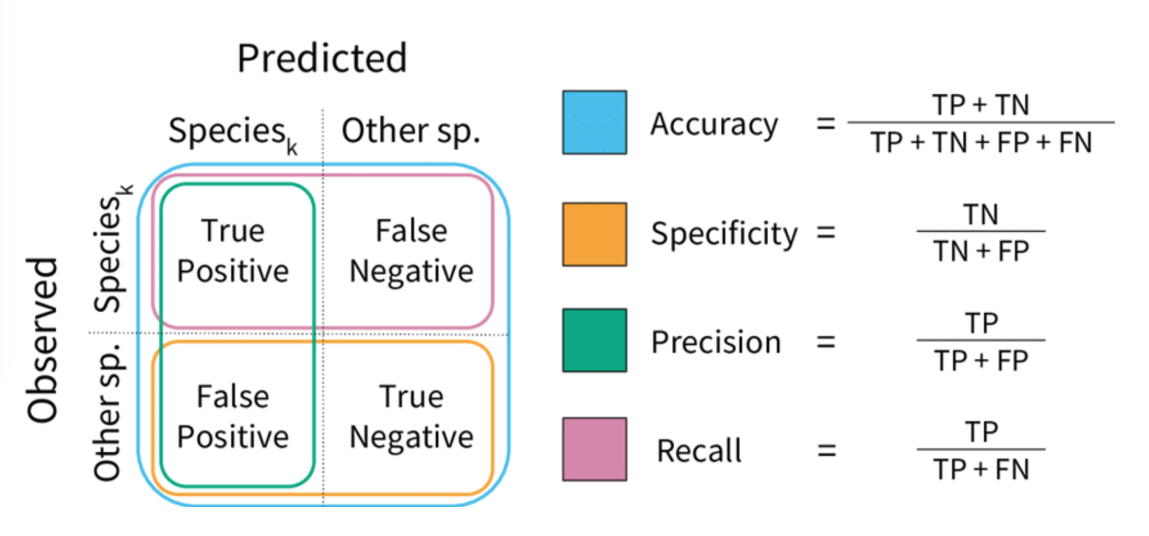
Estas métricas se basan en una tabla muy importante: la matriz de confusión.
Matriz de Confusión#
La matriz de confusión compara lo que el modelo predijo con la realidad.
Imagina que queremos clasificar si un cliente pagará un préstamo (sí = 1, no = 0).
Predicho Positivo |
Predicho Negativo |
|
|---|---|---|
Real Positivo |
TP (Verdadero Positivo) |
FN (Falso Negativo) |
Real Negativo |
FP (Falso Positivo) |
TN (Verdadero Negativo) |
TP: el cliente realmente pagó, y el modelo predijo que sí.
TN: el cliente no pagó, y el modelo predijo que no.
FP: el cliente no pagó, pero el modelo predijo que sí (error grave para el banco).
FN: el cliente pagó, pero el modelo predijo que no.
Ejemplo intuitivo:
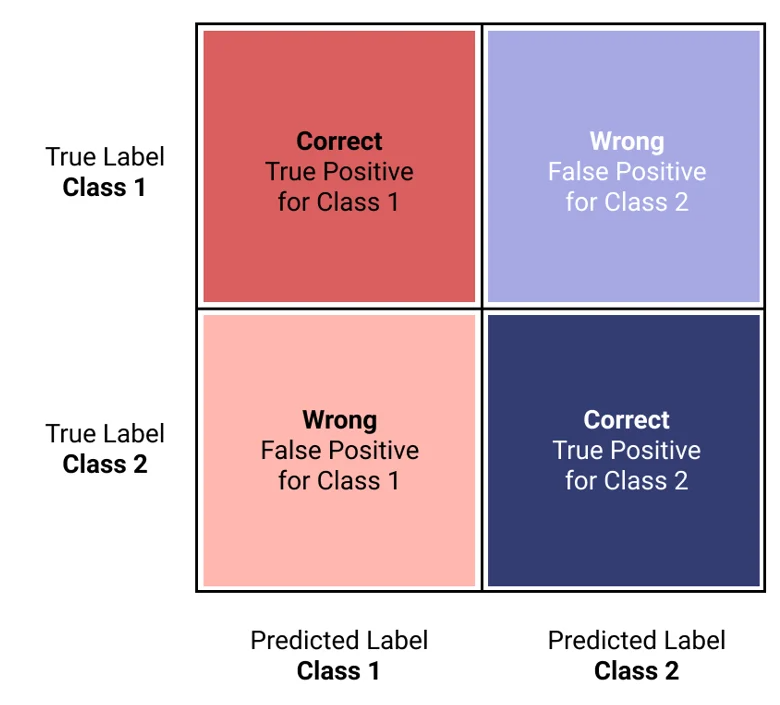
Un clasificador perfecto tendría solo TP y TN, es decir, solo valores en la diagonal de la matriz.
\(TP\) son los verdaderos positivos (True Positives) (correcto). La clase es positiva (clase 1) y el clasificador la reconoce correctamente como tal (verdadero positivo).
\(TN\) son los verdaderos negativos (True Negatives) (correcto). La clase es negativa (clase 0) y el clasificador la reconoce correctamente como tal (verdadero negativo).
\(FP\) son los falsos positivos (False Positives) (mal clasificado). La clase es negativa, pero el clasificador la etiqueta como positiva (falso positivo). Es un 0 clasificado como 1.
\(FN\) on los falsos negativos (False Negatives) (mal clasificado). La clase es positiva, pero el clasificador la etiqueta como negativa (falso negativo). Es un 1 clasificado como 0.
Cada fila en una matriz de confusión representa una clase real, mientras que cada columna representa una clase predicha.
MatrizConfusion#
MatrizConfusion2#
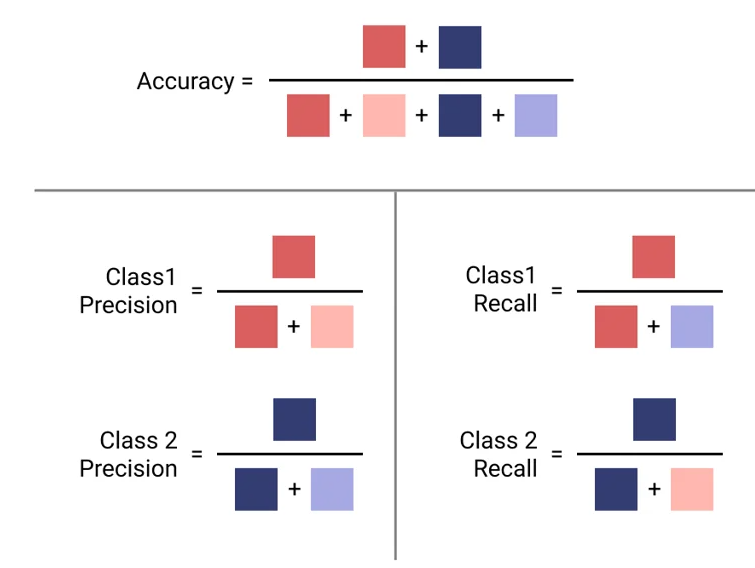
Accuracy (Exactitud)#
La exactitud es la métrica más conocida: mide qué porcentaje de veces acertó el modelo.
Fácil de interpretar.
Puede engañar si hay clases desbalanceadas.
La tasa de error de un clasificador (E) es la frecuencia de errores cometidos por el clasificador sobre un conjunto dado, es decir, la tasa de error es 1 menos Accuracy.
Ejemplo:
Si el 95% de los clientes paga el préstamo, un modelo que siempre predice “sí paga” tendrá 95% de accuracy, ¡pero no sirve para detectar morosos!
Precisión (Precision)#
👉 Mide qué proporción de los que el modelo predijo como positivos son realmente positivos.
De todos los que el modelo “metió al grupo positivo” (predicción) ¿cuántos eran verdaderos (gatos) y negativos (perros) (FP)? Se ve afectada por los Falsos Positivos: cuantos más Falsos Positivos haya, más baja será la precisión.
👉 Prefiero acusar poco, pero casi siempre con razón.
Evita dar “falsas alarmas”.
Importante cuando los falsos positivos son costosos.
Ejemplo:
En recomendaciones de productos en un e-commerce, preferimos que las sugerencias sean pocas pero correctas.
La precisión es la proporción de verdaderos positivos entre el total de predicciones positivas. Indica qué tan preciso es el modelo al predecir la clase positiva. En otras palabras, la precisión mide la exactitud de las predicciones positivas realizadas por el modelo.
La precisión se utiliza típicamente junto con otra métrica llamada recall, también conocida como sensibilidad o tasa de verdaderos positivos (TPR).
Recall o Sensibilidad#
👉 Mide qué proporción de los positivos reales fueron identificados correctamente como positivos.
De todos los gatos reales que había en la base de datos, ¿a cuántos logró encontrar el modelo y cuántos se le escaparon (FN)? Se ve afectado por los escapados (FN): cuantos más gatos se le escapen al modelo, más bajo será el recall.
👉 Prefiero casi no perder ningún gato (pocos FN), aunque me equivoque más marcando perros cómo gatos (FP).
Un FN puede encarecer crédito; un FN puede dejar sin ayuda a quien la necesita.
Evita “dejar pasar” casos importantes.
Importante cuando los falsos negativos son costosos.
Ejemplo:
En fraude financiero, es mejor atrapar a casi todos los fraudes (alto recall), aunque algunas transacciones legítimas sean marcadas como sospechosas.
La tensión entre Precisión y Recall#
Bajar el umbral de decisión: el modelo predice más positivos → sube el recall pero baja la precisión.
Subir el umbral de decisión: el modelo es más estricto → sube la precisión pero baja el recall.
Esto se llama trade-off entre precisión y recall.
La sensibilidad o recall es la proporción de verdaderos positivos entre el total de positivos reales. Mide la capacidad del modelo para identificar correctamente las instancias de la clase positiva.
A menudo es conveniente combinar la precisión y el recall en una sola métrica llamada F score, especialmente si necesitas una forma sencilla de comparar dos clasificadores. El F score es la media armónica de la precisión y el recall.
Ejemplos de aplicación para alto recall
Detección de Fraude: Si estás desarrollando un sistema para detectar fraudes en transacciones financieras, podrías preferir un alto recall. Es decir, quieres capturar todos los casos posibles de fraude, incluso si esto significa tener algunos falsos positivos (transacciones no fraudulentas clasificadas como fraudulentas).
Diagnóstico Médico: En un sistema de diagnóstico médico para detectar una enfermedad grave, podrías preferir un alto recall para asegurarte de que la mayoría de los casos de la enfermedad sean detectados, incluso si hay algunos falsos positivos. De manera similar, un diagnóstico médico incorrecto es a menudo más costoso que no tener diagnóstico, pero un diagnóstico incorrecto puede resultar en elegir un tratamiento que haga más daño que bien.
Por otro lado, en algunos casos la precisión es más importante que el recall. Por ejemplo, cuando compras algo en un sitio web, a menudo aparece un mensaje como: “Los clientes que compraron X también compraron Y”. En este contexto, el valor del recall no es tan importante porque no es crucial que el sistema identifique todos los artículos que los clientes podrían querer. Lo fundamental es que los clientes estén satisfechos con las recomendaciones que reciben. Si las recomendaciones son precisas y relevantes, los clientes estarán más inclinados a considerar y aceptar estas sugerencias. De lo contrario, si las recomendaciones son inexactas o irrelevantes, los clientes las ignorarán en el futuro, disminuyendo la efectividad del sistema de recomendaciones.
F1 Score#
El F1 Score combina precisión y recall en una sola métrica.
Es la media armónica de ambas:
Útil cuando hay clases desbalanceadas.
Solo será alto si ambos (precisión y recall) son altos.
La puntuación F1 es la media armónica de la precisión y la sensibilidad. Es útil cuando se necesita un equilibrio entre precisión y sensibilidad. Es especialmente útil en contextos donde no solo es importante capturar la mayor cantidad de instancias positivas posibles (recall), sino también asegurarse de que las predicciones positivas sean correctas (precisión).
El clasificador solo obtendrá una alta F score si tanto el recall como la precisión son altos.
El F score favorece a los clasificadores que tienen precisión y recall similares. Esto no siempre es lo que deseas: en algunos contextos te importa más la precisión, y en otros contextos realmente te importa el recall. Por ejemplo, si entrenas un clasificador para detectar videos que sean seguros para niños, probablemente prefieras un clasificador que rechace muchos buenos videos (bajo recall) pero mantenga solo los seguros (alta precisión), en lugar de un clasificador que tenga un recall mucho mayor pero permita que aparezcan algunos videos realmente inapropiados en tu producto (en tales casos, incluso podrías querer agregar una revisión humana para verificar la selección de videos del clasificador) (Géron, 2019).
Por otro lado, supongamos que entrenas un clasificador para detectar ladrones en imágenes de vigilancia: probablemente esté bien si tu clasificador tiene solo un 30% de precisión siempre y cuando tenga un 99% de recall (claro, los guardias de seguridad recibirán algunas alertas falsas, pero casi todos los ladrones serán atrapados).
Desafortunadamente, no puedes tener ambos al mismo tiempo: aumentar la precisión reduce el recall, y viceversa. Esto se llama la compensación entre precisión y recall.
Especificidad#
La especificidad es lo opuesto al recall, pero aplicada a la clase negativa.
👉 Mide qué proporción de los negativos reales fueron identificados correctamente como negativos.
De todos los perros reales que había en la base de datos, ¿a cuántos logró reconocer el modelo como perros y cuántos se le colaron en el grupo de gatos (FP)? Se ve afectada por los colados (FP): cuantos más perros se metan por error como gatos, más baja será la especificidad.
Se usa mucho en medicina junto con el recall.
Curva Precisión / Recall#
Si movemos el umbral de decisión del modelo, la precisión y el recall cambian.
Umbral bajo:
Alta recall (detecta casi todos los positivos).
Baja precisión (muchos falsos positivos).
Umbral alto:
Alta precisión.
Baja recall (se escapan muchos positivos).
Visualización: una curva que muestra la relación entre precisión y recall según el umbral.
Muy útil cuando la clase positiva es rara (por ejemplo, fraude bancario).
Metricas#
Metricas_2#
Metricas_2_1#
Curva ROC y AUC-ROC#
La curva ROC (Receiver Operating Characteristic) grafica:
Eje Y: Recall (TPR). Representa a los gatos encontrados correctamente por el modelo, Verdaderos Positivos.
Eje X: Tasa de falsos positivos (FPR = 1 - Specificity). Representa a los Falsos Positivos (perros que el modelo metió por error como gatos).
Cada punto de la curva ROC muestra un umbral de decisión diferente. A medida que bajo el umbral, el modelo detecta más gatos (↑ Recall), pero también deja entrar más perros colados (FP) (↑ FPR).
El AUC (Área Bajo la Curva ROC) mide la capacidad global del modelo para distinguir entre clases. Resume en un solo número qué tan bien el modelo separa gatos vs perros:
AUC = 1: modelo perfecto.
AUC = 0.5: modelo aleatorio.
Un AUC de 0,80 significa que, si tomas un gato y un perro al azar, hay un 80% de probabilidad de que el modelo le asigne mayor score al gato que al perro. Significa que el modelo diferencia bastante bien entre gatos y perros, aunque todavía se le cuelan algunos perros y se le escapan algunos gatos en ciertos umbrales.
Ejemplo financiero: comparar diferentes modelos de scoring crediticio y elegir el que mejor separa buenos de malos pagadores.
La AUC-ROC mide la capacidad del modelo para distinguir entre clases, representando el área bajo la curva ROC. Esta curva grafica la tasa de verdaderos positivos contra la tasa de falsos positivos en diferentes umbrales de decisión. La FPR es la proporción de instancias negativas clasificadas incorrectamente como positivas, y es igual a 1 menos la especificidad (tasa de verdaderos negativos).
Una curva ROC ideal se aleja lo más posible de la línea punteada de un clasificador aleatorio, dirigiéndose hacia la esquina superior izquierda. Un clasificador perfecto tiene una AUC-ROC de 1, mientras que uno aleatorio tiene una AUC-ROC de 0.5.
La elección entre la curva ROC y la curva precisión/recall depende del contexto: se prefiere la curva precisión/recall cuando la clase positiva es rara o cuando los falsos positivos son más importantes que los falsos negativos; en otros casos, se usa la curva ROC.
CurvaROC#
Resumen:#
Matriz de confusión: la base de todas las métricas.
Accuracy: bueno si las clases están balanceadas.
Precisión: importante cuando FP son costosos (ej. dar un préstamo a alguien riesgoso).
Recall: importante cuando FN son costosos (ej. no detectar un fraude).
F1 Score: balance entre precisión y recall.
Especificidad: detección de la clase negativa.
Curva PR: útil en clases desbalanceadas.
Curva ROC y AUC: visión global de la capacidad del modelo.
Ejemplo: cuando una métrica “alta” es engañosa (Fraude y Medicina)#
En problemas desbalanceados (pocos positivos), una métrica alta puede dar una falsa sensación de buen desempeño.
A continuación, dos casos didácticos con matrices de confusión, cálculo de métricas y conclusión práctica.
Caso 1: Detección de fraudes (clase positiva = fraude)#
Contexto: 10 000 transacciones, solo 100 son fraude (1%).
Modelo A (ingenuo): siempre predice “no fraude”.
Matriz de confusión (Modelo A):
Predicho Positivo |
Predicho Negativo |
|
|---|---|---|
Real Positivo |
0 |
100 |
Real Negativo |
0 |
9 900 |
Accuracy: ((0 + 9 900) / 10 000 = 0.990) (99%)
Precision: indefinida (no predice positivos) → por convención 0
Recall (Sensibilidad): (0 / (0 + 100) = 0) (0%)
Conclusión: la accuracy es altísima (99%), pero el modelo no detecta ningún fraude (recall = 0%).
Métrica que importa aquí: Recall (y también PR-AUC) porque perder fraudes (FN) es costoso.
Modelo B (más útil): detecta 80 de 100 fraudes, pero comete 200 falsos positivos.
Matriz de confusión (Modelo B):
Predicho Positivo |
Predicho Negativo |
|
|---|---|---|
Real Positivo |
80 |
20 |
Real Negativo |
200 |
9 700 |
Accuracy: ((80 + 9 700) / 10 000 = 0.978) (97.8%) ← menor que antes
Precision: (80 / (80 + 200) = 0.286) (28.6%)
Recall: (80 / (80 + 20) = 0.80) (80%)
F1: (2·(0.286·0.80)/(0.286+0.80) ≈ 0.421) (42.1%)
Conclusión: aunque la accuracy bajó (de 99% a 97.8%), el modelo B es mucho mejor para el objetivo: captura el 80% de los fraudes.
Qué mirar: en fraude, prioriza Recall (no perder fraudes) y F1 / PR-AUC sobre Accuracy.
Caso 2: Tamizaje en medicina (clase positiva = enfermedad)#
Contexto: 5 000 pacientes; 250 tienen la enfermedad (5%).
Modelo C (muy “conservador”): solo marca positivos cuando está casi seguro.
Matriz de confusión (Modelo C):
Predicho Positivo |
Predicho Negativo |
|
|---|---|---|
Real Positivo |
100 |
150 |
Real Negativo |
50 |
4 700 |
Accuracy: ((100 + 4 700) / 5 000 = 0.96) (96%)
Precision: (100 / (100 + 50) = 0.667) (66.7%) ← alta
Recall: (100 / (100 + 150) = 0.40) (40%) ← baja
Conclusión: la precisión es alta, pero el modelo deja pasar 60% de los casos enfermos (FN altos).
Riesgo clínico: pacientes no detectados pueden no recibir tratamiento oportuno.
Qué mirar: en tamizaje, prioriza Recall (sensibilidad). Ajusta el umbral para incrementar recall, aunque baje la precisión, y compénsalo con segunda prueba (confirmatoria) para filtrar falsos positivos.
Lecciones clave (qué métrica usar según el objetivo)#
Fraude, seguridad, salud pública, fallas críticas: prioriza Recall (evitar FN). Complementa con F1 y PR-AUC.
Recomendadores, moderación estricta, contenido infantil: prioriza Precision (evitar FP). Ajusta umbral y considera revisión humana.
Clases balanceadas y costo de error similar: Accuracy puede ser útil, pero siempre verifica la matriz de confusión.
Desbalance severo: prefiere PR-AUC sobre ROC-AUC y reporta Precision/Recall a múltiples umbrales.