Funciones de activación

En una red neuronal, las funciones de activación determinan cómo se combinan y transforman las señales que llegan a cada neurona.

Son las encargadas de introducir no linealidad en el modelo, permitiendo que la red aprenda relaciones complejas entre las variables de entrada y salida.

Sin funciones de activación, la red se comportaría como una simple combinación lineal de las entradas,

sin importar cuántas capas tuviera.

Esto limitaría su capacidad de representación, ya que una secuencia de transformaciones lineales sigue siendo lineal.

Propósito principal:

• Introducir no linealidad para que la red pueda aprender patrones más complejos.

• Controlar la escala y la dirección de la señal que se propaga.

• Afectar el flujo del gradiente durante el entrenamiento, influyendo en la velocidad y estabilidad del aprendizaje.

Ejemplo general:

La salida de una neurona se calcula como:

\(y = f(Wx + b)\)

donde:

• \(W\) son los pesos,

• \(x\) es el vector de entradas,

• \(b\) es el sesgo (bias),

• \(f\) es la función de activación.

Intuición:

Las funciones de activación actúan como “filtros” que deciden qué señales pasan y cuáles no.

Su elección afecta directamente la capacidad de la red para aprender, la rapidez del entrenamiento

y la estabilidad del descenso del gradiente.

Las funciones de activación controlan la información que pasa a través de la red (forward pass).

Las redes neuronales artificiales son capaces de aprender relaciones no lineales gracias a la combinación de funciones de activación no lineales en las múltiples capas.

Las funciones de activación más usadas son sigmoide, ReLU y tangente hiperbólica (tanh), pero existen muchas más y cada vez aparecen nuevas variaciones.

Importancia de la Derivada en las Funciones de Activación

Las funciones de activación no solo transforman las salidas de las neuronas,

también determinan cómo fluye el gradiente durante el entrenamiento.

En el descenso del gradiente, los pesos se actualizan según:

\(W^{(nextStep)} = W - \eta \times \frac{\partial}{\partial W} MSE(W)\)

Aquí, la derivada de la función de activación forma parte de la cadena de derivadas que se calculan en la retropropagación del error (backpropagation).

Por qué la derivada es importante:

• Si la derivada es grande, los pesos cambian bruscamente → el aprendizaje puede volverse inestable (explosión del gradiente).

• Si la derivada es muy pequeña, los pesos apenas cambian → el modelo deja de aprender (desvanecimiento del gradiente).

Explosión del gradiente:

Ocurre cuando las derivadas se multiplican y crecen exponencialmente al retropropagar el error.

Esto hace que los pesos aumenten sin control, generando oscilaciones o pérdida de convergencia.

Desvanecimiento del gradiente:

Sucede cuando las derivadas son menores que 1 y se multiplican muchas veces hacia atrás,

volviéndose casi cero en capas profundas.

El resultado es que las capas iniciales dejan de actualizarse.

Ejemplos:

• Funciones como sigmoide o tanh pueden causar desvanecimiento del gradiente porque su pendiente se aplana en los extremos.

• Funciones como ReLU o SELU reducen este problema al mantener derivadas más grandes y estables.

Funciones de Activación en Keras

1. Sigmoide:

La función sigmoide convierte cualquier valor real en un número entre 0 y 1, lo que la hace útil para representar probabilidades en modelos de clasificación.

Definición:

\(\sigma(x) = \frac{1}{1 + e^{-x}}\)

Su forma es una curva en “S”, donde los valores grandes de \(x\) se acercan a 1 y los valores muy negativos se acercan a 0.

En la sigmoide todas las activaciones son positivas. Entonces, cuando las neuronas de una capa alimentan a la siguiente, todas las entradas siguientes son del mismo signo (positivas).

Esto genera dos efectos negativos:

• Desbalance en los gradientes: el promedio de las salidas nunca es 0, lo que provoca un sesgo en la retropropagación.

• Gradientes más pequeños: al no haber cancelaciones entre positivos y negativos, los gradientes se acumulan con un mismo signo y tienden a disminuir rápidamente en magnitud.

Derivada:

\(\sigma'(x) = \sigma(x) \times (1 - \sigma(x))\)

La derivada indica qué tanto cambia la salida cuando cambia la entrada.

En la sigmoide, la pendiente es mayor alrededor de 0 y casi nula en los extremos, lo que puede causar el problema del desvanecimiento del gradiente.

Relación con el descenso del gradiente:

En el proceso de entrenamiento, los pesos se actualizan según:

\(W^{(nextStep)} = W - \eta \times \frac{\partial}{\partial W} MSE(W)\)

Cuando se usa la sigmoide, la derivada \(\sigma'(x)\) forma parte de ese gradiente.

Si la pendiente es muy pequeña (valores saturados), el gradiente se vuelve casi cero y el aprendizaje se vuelve lento.

Intuición:

La sigmoide “suaviza” la salida y ayuda a representar probabilidades,

pero si las activaciones son muy altas o bajas, el modelo aprende más despacio porque el gradiente deja de propagarse eficazmente.

En Keras: "sigmoid"

import numpy as np
import matplotlib.pyplot as plt

sigmoid = lambda z: 1 / (1 + np.exp(-z))

z = np.linspace(-10, 10, 1000)

plt.figure(dpi=100)
plt.plot(z, sigmoid(z));

Derivada:

\[\frac{\partial \sigma(z)}{\partial z} = \sigma(z)(1-\sigma(z))\]

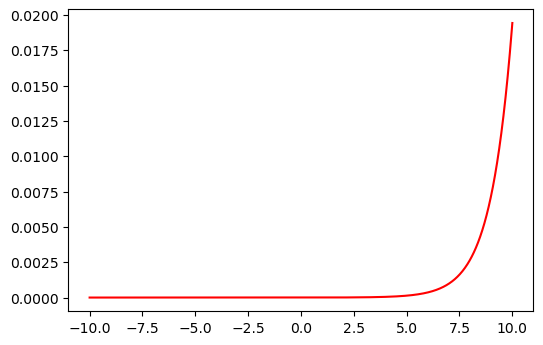
dsigmoid = sigmoid(z) * (1 - sigmoid(z))

plt.figure(dpi=100)
plt.plot(z, dsigmoid, "r-");

2. Tangente hiperbólica:

La tangente hiperbólica (tanh) es una función de activación que transforma los valores reales en un rango entre -1 y 1.

Definición:

\(tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}\)

Su forma es una curva en “S”, similar a la sigmoide, pero centrada en cero.

Esto permite que las salidas puedan ser negativas o positivas, lo cual mejora la propagación del gradiente en redes profundas.

En tanh las neuronas pueden tener activaciones positivas o negativas. El resultado es que las entradas a la siguiente capa están centradas alrededor de 0, es decir, la red tiene valores tanto positivos como negativos balanceados. Las derivadas (que se multiplican durante el backpropagation) tienen valores más equilibrados.

Derivada:

\(tanh'(x) = 1 - tanh^2(x)\)

La derivada es máxima en el centro (cuando \(x \approx 0\)) y disminuye hacia los extremos, donde la función se satura.

Relación con el descenso del gradiente:

En el proceso de actualización de los pesos:

\(W^{(nextStep)} = W - \eta \times \frac{\partial}{\partial W} MSE(W)\)

la derivada de la función de activación forma parte del gradiente.

Cuando \(tanh(x)\) está saturada (muy cerca de -1 o 1), su derivada es pequeña y el gradiente se atenúa, ralentizando el aprendizaje.

Intuición:

La función tanh suele ser preferida frente a la sigmoide porque su salida está centrada en cero, lo que hace que el descenso del gradiente sea más eficiente y estable, aunque también puede sufrir el problema del desvanecimiento del gradiente en valores extremos.

En Keras: "tanh"

\[tanh(z) = \frac{sinh(z)}{cosh(z)}=\frac{exp^z-exp^{-z}}{exp^z+exp^{-z}}\]

tanh = lambda z: (np.exp(z) - np.exp(-z)) / (np.exp(z) + np.exp(-z))

plt.figure(dpi=100)
plt.plot(z, tanh(z));

Derivada:

\[\frac{\partial \tanh(z)}{\partial z} = 1-tan(z)^2\]

dtanh = 1 - tanh(z) ** 2

plt.figure(dpi=100)
plt.plot(z, dtanh, "r-");

3. ReLU:

La ReLU es la función de activación más usada en redes neuronales profundas por su sencillez y eficiencia.

Definición:

\(ReLU(x) = \begin{cases} 0, & \text{si } x < 0 \\ x, & \text{si } x \ge 0 \end{cases}\)

La ReLU deja pasar los valores positivos tal como son y anula los negativos.

Esto introduce no linealidad sin saturar los gradientes como la sigmoide o la tanh.

Derivada:

\(ReLU'(x) = \begin{cases} 0, & \text{si } x < 0 \\ 1, & \text{si } x \ge 0 \end{cases}\)

Durante el descenso del gradiente, la derivada determina cómo se ajustan los pesos:

\(W^{(nextStep)} = W - \eta \times \frac{\partial}{\partial W} MSE(W)\)

Con ReLU, los gradientes se mantienen grandes cuando \(x > 0\), acelerando el aprendizaje,

mientras que en \(x < 0\) se detiene la actualización (gradiente cero).

Intuición:

ReLU actúa como un “interruptor” que activa solo las neuronas con salidas positivas,

haciendo el modelo más eficiente y reduciendo el riesgo de desvanecimiento del gradiente,

aunque puede causar el problema de las neuronas muertas cuando muchas entradas son negativas.

En Keras: "relu"

\[ReLU(z) = max(z,0)\]

ReLU (Rectified Linear Units) es la función de activación más utilizada en el aprendizaje profundo.

• Mejor propagación del gradiente: menos problemas de fuga de gradiente en comparación con las funciones de activación sigmoide y thanh.

• Cálculo eficiente: ya que solo es comparación, suma y multiplicación.

• Presenta varias unidades (neuronas) inactivas porque arroja valores de cero en gran parte de la curva.

• Tiene otra gran ventaja en que no tiene valor de salida máximo lo que ayuda a reducir algunos problemas durante el Gradient Descent.

Desventaja:

• Es diferenciable en cualquier valor, pero no en 0, el valor de la derivada en este punto puede elegirse arbitrariamente a ser 0 o 1.

• Cuando \(z=0\), la pendiente cambia abruptamente, lo que puede ocasionar que el Gradient Descent rebote.

• Debido a que no tiene límite superior, es infinito, conduce a veces a nodos inutilizables.

relu = lambda z: np.maximum(z, 0)

plt.figure(dpi=100)
plt.plot(z, relu(z));

Derivada:

• Si \(z<0\):

\[\frac{\partial ReLU(z)}{\partial z} = 0\]

• Si \(z>0\):

\[\frac{\partial ReLU(z)}{\partial z} = 1\]

drelu = (z > 0) * 1

plt.figure(dpi=100)
plt.plot(z, drelu, "r-");

4. ELU:

La ELU es una mejora de la ReLU que permite valores negativos suaves en lugar de ceros,

lo que ayuda a mantener activas más neuronas y reduce el problema del gradiente desapareciente.

Definición:

\(ELU(x, \alpha) = \begin{cases} x, & \text{si } x \ge 0 \\ \alpha \left(e^{x} - 1\right), & \text{si } x < 0 \end{cases}\)

donde \(\alpha\) controla cuánto se extiende la parte negativa (típicamente \(\alpha = 1\)).

Derivada:

\(ELU'(x, \alpha) = \begin{cases} 1, & \text{si } x \ge 0 \\ ELU(x, \alpha) + \alpha, & \text{si } x < 0 \end{cases}\)

Durante el descenso del gradiente, los pesos se actualizan con:

\(W^{(nextStep)} = W - \eta \times \frac{\partial}{\partial W} MSE(W)\)

En este proceso, la derivada de ELU mantiene un flujo continuo del gradiente,

permitiendo que las neuronas con valores negativos sigan ajustando sus pesos,

a diferencia de ReLU, donde el gradiente se anula por completo en \(x < 0\).

Intuición:

ELU actúa como una ReLU suavizada:

• Para \(x > 0\), se comporta igual que ReLU (lineal).

• Para \(x < 0\), usa una curva exponencial que evita que las neuronas mueran.

El resultado es un aprendizaje más estable y rápido gracias a una propagación de gradientes más fluida.

En Keras: "elu"

• Si \(z>0\):

\[ELU(z) = z\]

• Si \(z<=0\):

\[ELU(z) = \alpha(exp^z-1)\]

alpha = 1.5

def elu(x):
    if x > 0:
        return x
    else:
        return alpha * (np.exp(x) - 1)

elu = [elu(z) for z in np.linspace(-10, 10, 1000)]

plt.figure(dpi=100)
plt.plot(z, elu);

Derivada:

• Si \(z>0\):

\[\frac{\partial ELU(z)}{\partial z} = 1\]

• Si \(z<=0\):

\[\frac{\partial ELU(z)}{\partial z} = \alpha exp(z)\]

def delu(x):
    if x > 0:
        return 1
    else:
        return alpha * np.exp(x)

delu = [delu(z) for z in np.linspace(-10, 10, 1000)]

plt.figure(dpi=100)
plt.plot(z, delu, "r-");

5. SELU:

La SELU es una función de activación autorreguladora que mantiene automáticamente la media y la varianza de las activaciones,

lo que ayuda a que la red se mantenga estable durante el entrenamiento.

Definición:

\(SELU(x) = \lambda \begin{cases} x, & \text{si } x \ge 0 \\ \alpha (e^{x} - 1), & \text{si } x < 0 \end{cases}\)

donde los valores típicos son \(\lambda = 1.0507\) y \(\alpha = 1.67326\).

Derivada:

\(SELU'(x) = \lambda \begin{cases} 1, & \text{si } x \ge 0 \\ \alpha e^{x}, & \text{si } x < 0 \end{cases}\)

Durante el descenso del gradiente, la actualización de los pesos sigue la regla:

\(W^{(nextStep)} = W - \eta \times \frac{\partial}{\partial W} MSE(W)\)

Gracias a sus constantes \(\lambda\) y \(\alpha\),

SELU normaliza las activaciones internamente, reduciendo la necesidad de técnicas adicionales como batch normalization.

Intuición:

SELU combina las ventajas de ELU y la normalización automática:

• Aumenta la estabilidad del entrenamiento.

• Evita que los gradientes desaparezcan o exploten.

• Mantiene la media cercana a 0 y la varianza alrededor de 1.

En Keras: "selu"

• Si \(z>0\):

\[SELU(z) = \lambda z\]

• Si \(z<=0\):

\[SELU(z) = \lambda\alpha(exp^z-1)\]

Donde \(\alpha=1.67326324\) y \(\lambda=1.05070098\) son constantes predefinidas.

SELU (Scaled Exponencial Linear Unit) es otra variación de ReLU.

Podría resolver el problema de la fuga y explosión del gradiente con una red compuesta exclusivamente con capas con esta función de activación. La salida de cada capa tendrá a conservar la media cero y desviación estándar de 1.

Desventaja:

• Solo para redes neuronales compuestas por capas densas. Puede que no funcione para redes neuronales convolucionales.

• Los pesos de cada capa oculta deben inicializarse mediante la inicialización normal de LeCun.

• Las variables de entrada (inputs) deben estar normalizadas con media 0 y desviación estándar 1.

alpha = 1.67326324
LAMBDA = 1.05070098

def selu(x):
    if x >= 0:
        return LAMBDA * x
    else:
        return LAMBDA * alpha * (np.exp(x) - 1)

selu = [selu(z) for z in np.linspace(-10, 10, 1000)]

plt.figure(dpi=100)
plt.plot(selu);

Derivada:

• Si \(z>0\):

\[\frac{\partial SELU(z)}{\partial z} = \lambda\]

• Si \(z<=0\):

\[\frac{\partial SELU(z)}{\partial z} = \lambda\alpha exp^z\]

def dselu(x):
    if x > 0:
        return LAMBDA
    else:
        return LAMBDA * alpha * np.exp(x)

dselu = [dselu(z) for z in np.linspace(-10, 10, 1000)]

plt.figure(dpi=100)
plt.plot(z, dselu, "r-");

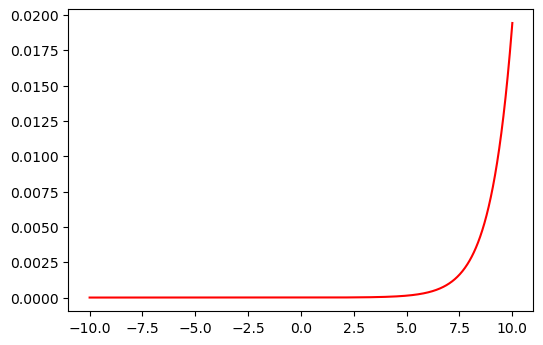
6. Softmax:

La Softmax se utiliza principalmente en la capa de salida de redes neuronales de clasificación multiclase.

Convierte un vector de valores reales en un vector de probabilidades que suman 1.

Definición:

\(Softmax(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{K} e^{z_j}}\)

donde \(z_i\) es la salida del modelo para la clase \(i\) y \(K\) es el número total de clases.

Cada valor \(e^{z_i}\) se normaliza dividiéndolo entre la suma de todas las exponenciales,

haciendo que el resultado esté entre 0 y 1 y se interprete como una probabilidad.

Derivada:

La derivada de Softmax es una matriz (Jacobiano) que refleja cómo cambia cada probabilidad con respecto a cada entrada:

\(\frac{\partial Softmax(z_i)}{\partial z_j} = Softmax(z_i) \times (\delta_{ij} - Softmax(z_j))\)

donde \(\delta_{ij}\) es 1 si \(i = j\) y 0 en caso contrario.

Relación con el descenso del gradiente:

En la etapa de entrenamiento, los pesos se actualizan según:

\(W^{(nextStep)} = W - \eta \times \frac{\partial}{\partial W} MSE(W)\)

Cuando se usa Softmax junto con la entropía cruzada como función de pérdida,

la derivada se simplifica, lo que acelera y estabiliza el descenso del gradiente.

Intuición:

Softmax convierte las salidas del modelo en probabilidades interpretables.

Resalta la clase más probable y atenúa las demás,

permitiendo que el modelo aprenda distribuciones de probabilidad en lugar de valores arbitrarios.

En Keras: "softmax"

\[s(z) = \frac{exp^z}{\sum{exp^z}}\]

softmax = lambda z: np.exp(z) / sum(np.exp(z))

plt.figure(dpi=100)
plt.plot(z, softmax(z));

Derivada:

\[\frac{\partial s(z)}{\partial z} = s(z)(1-s(z))\]

dsoftmax = softmax(z) * (1 - softmax(z))

plt.figure(dpi=100)
plt.plot(z, dsoftmax, "r-");