Frontera Eficiente#
#!pip install yfinance
import yfinance as yf
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
# Quitar advertencias (warming):
import warnings
warnings.filterwarnings("ignore")
# Descargar acciones: KO, TSLA, WMT y FDX.
# Definir qué acciones descargar y las fechas:
stocks = ["KO", "TSLA", "WMT", "FDX"]
start = "2019-12-01" # Fecha inicial para descargar
end = "2025-01-01" # Fecha final para descargar
# Descargar los datos desde Yahoo Finance: datos mensuales.
data = yf.download(["KO", "TSLA", "WMT", "FDX"], start=start, end=end, interval="1mo")[
"Close"].dropna()
# Cálculo de los rendimientos: mensuales.
returns_stocks = data.pct_change().dropna()
# Rendimientos esperados:
returns_stocks_mean = returns_stocks.mean()
# Volatilidades: mensuales
volatility = returns_stocks.std()
# Correlaciones:
correlation = returns_stocks.corr()
# Descargar la tasa libre de riesgo (rendimiento de los T-Bills a 3 meses)
t_bill_rate_data = yf.download("^IRX", start=start, end=end, interval="1mo")[
"Close"].dropna()
# La tasa viene en porcentaje, la convertimos a decimal
t_bill_rate = t_bill_rate_data / 100
# Rendimiento esperado anual de Rf:
Rf = t_bill_rate.mean()
# Rf mensual:
Rf = (1 + Rf) ** (1 / 12) - 1
# Indicador Sharpe:
sharpe_ratio = (returns_stocks_mean - Rf[0]) / volatility
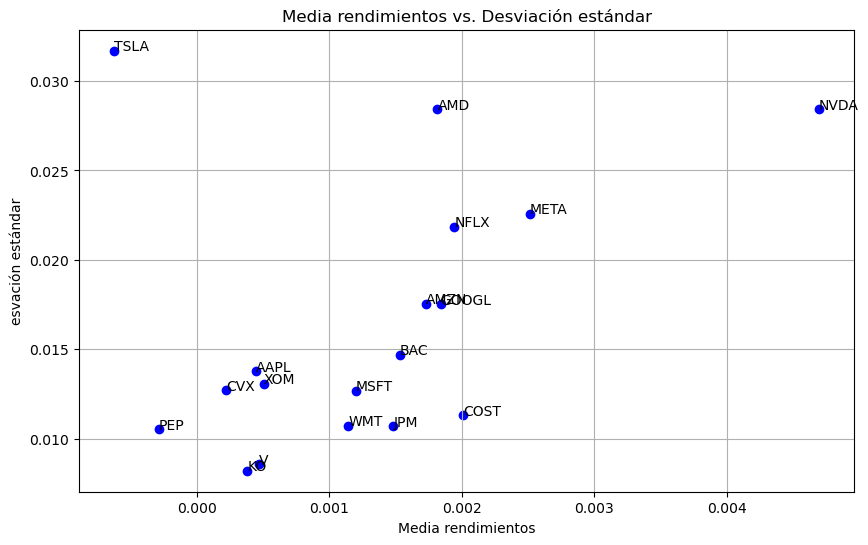
# Gráfico scatter de volatilidad Vs. Rendimiento de las acciones con los nombres de cada una:
plt.figure(figsize=(8, 4))
for stock in stocks:
plt.scatter(volatility[stock], returns_stocks_mean[stock], label=stock)
# Etiquetar cada punto con el nombre de la acción
plt.annotate(
stock,
(volatility[stock], returns_stocks_mean[stock]),
textcoords="offset points",
xytext=(0, 10),
ha="center",
)
plt.xlabel("Volatilidad")
plt.ylabel("Rendimiento Esperado")
plt.title("Volatilidad Vs. Rendimiento de las Acciones")
plt.legend()
plt.grid(True)
plt.show()
[*******************100%*********************] 4 of 4 completed [*******************100%*********************] 1 of 1 completed
# Verificar cantidad de datos:
print("\nCantidad de datos acciones: \n", data.shape)
# Rendimientos esperados:
print("\n Rendimientos esperados acciones: \n", returns_stocks_mean)
# Volatilidades:
print("\n Volatilidades acciones: ", volatility)
# Correlaciones:
print("\n Correlaciones acciones e índice: \n", correlation)
# Tasa libre de riesgo: mensual
print("\n Tasa libre de riesgo mensual:", Rf[0])
# Indicador Sharpe:
print("\n Indicador Sharpe: \n", sharpe_ratio)
Cantidad de datos acciones:
(62, 4)
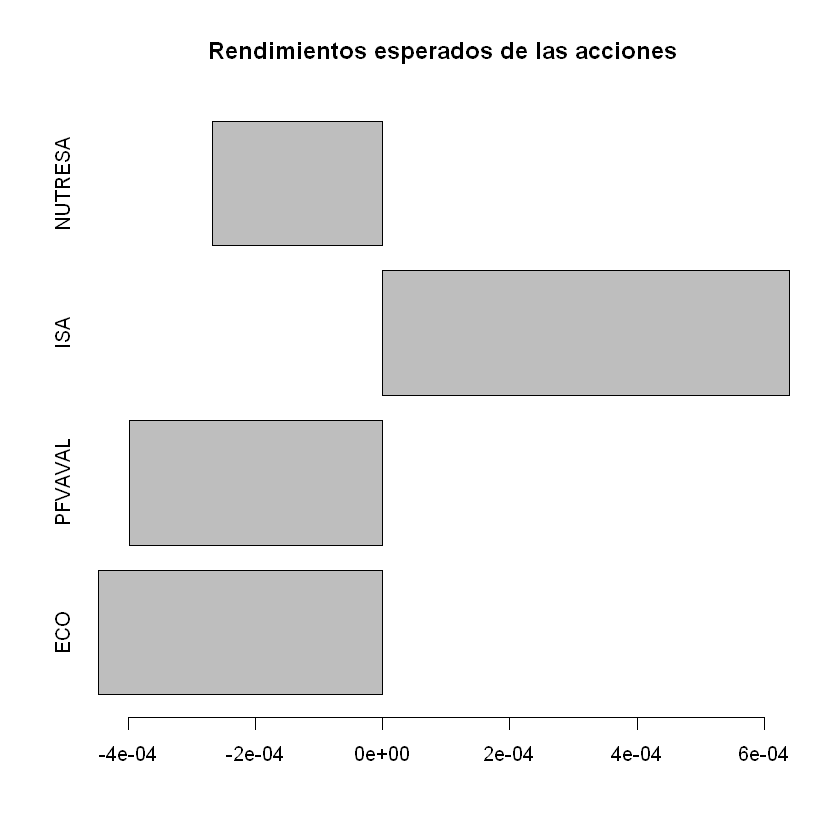
Rendimientos esperados acciones:
FDX 0.014518
KO 0.003734
TSLA 0.065867
WMT 0.016545
dtype: float64
Volatilidades acciones: FDX 0.103461
KO 0.054229
TSLA 0.219861
WMT 0.056346
dtype: float64
Correlaciones acciones e índice:
FDX KO TSLA WMT
FDX 1.000000 0.439545 0.328314 0.273771
KO 0.439545 1.000000 0.138847 0.354995
TSLA 0.328314 0.138847 1.000000 0.256786
WMT 0.273771 0.354995 0.256786 1.000000
Tasa libre de riesgo mensual: 0.001796736557855283
Indicador Sharpe:
FDX 0.122962
KO 0.035725
TSLA 0.291410
WMT 0.261746
dtype: float64
Frontera Eficiente:#
Simulación de portafolios aleatorios:
# Número de simulaciones de portafolios
num_portfolios = 10000
# Inicializar listas para almacenar métricas de portafolios
port_returns = []
port_volatility = []
port_sharpe = []
port_weights = []
# Matriz de covarianza mensual
cov_matrix = returns_stocks.cov()
np.random.seed(42)
for _ in range(num_portfolios):
# Generar pesos aleatorios y normalizarlos para que sumen 1
weights = np.random.random(len(stocks))
weights /= np.sum(weights)
# Calcular rendimiento del portafolio
port_ret = np.sum(weights * returns_stocks.mean())
# Calcular volatilidad del portafolio
port_vol = np.sqrt(np.dot(weights.T, np.dot(cov_matrix, weights)))
# Calcular el Sharpe Ratio
sharpe_ratio = (port_ret - Rf[0]) / port_vol
# Guardar resultados
port_returns.append(port_ret)
port_volatility.append(port_vol)
port_sharpe.append(sharpe_ratio)
port_weights.append(weights)
# Crear DataFrame con los resultados
portfolios = pd.DataFrame(
{"Return": port_returns, "Volatility": port_volatility, "Sharpe Ratio": port_sharpe}
)
# Identificar el portafolio con el máximo Sharpe Ratio
max_sharpe_idx = portfolios["Sharpe Ratio"].idxmax()
optimal_portfolio = portfolios.iloc[max_sharpe_idx]
# Identificar el portafolio con la mínima volatilidad
min_vol_idx = portfolios["Volatility"].idxmin()
min_vol_portfolio = portfolios.iloc[min_vol_idx]
Graficar la Frontera Eficiente:
plt.figure(figsize=(10, 6))
plt.scatter(
portfolios["Volatility"],
portfolios["Return"],
c=portfolios["Sharpe Ratio"],
cmap="viridis",
alpha=0.7,
)
plt.colorbar(label="Sharpe Ratio")
plt.scatter(
optimal_portfolio["Volatility"],
optimal_portfolio["Return"],
c="red",
marker="*",
s=200,
label="Máx Sharpe Ratio",
)
plt.scatter(
min_vol_portfolio["Volatility"],
min_vol_portfolio["Return"],
c="blue",
marker="D",
s=100,
label="Mínima Volatilidad",
)
for stock in stocks:
plt.scatter(volatility[stock], returns_stocks_mean[stock], label=stock)
# Etiquetar cada punto con el nombre de la acción
plt.annotate(
stock,
(volatility[stock], returns_stocks_mean[stock]),
textcoords="offset points",
xytext=(0, 10),
ha="center",
)
plt.xlabel("Volatilidad")
plt.ylabel("Retorno Esperado")
plt.title("Frontera Eficiente de Markowitz")
plt.legend()
plt.grid(True)
plt.show()
Frontera Eficiente con PyPortfolioOpt:#
#!pip install PyPortfolioOpt -q
from pypfopt import EfficientFrontier, risk_models, expected_returns, plotting
# Calcular la matriz de covarianzas a returns_stocks:
cov_matrix = risk_models.sample_cov(
returns_stocks, returns_data=True, frequency=1
) # frequency=1 para que no lo convierta en el tiempo
# cov_matrix es la matriz de Covarianzas-Varianzas
# Crear el objeto EfficientFrontier y optimizar para maximizar el Sharpe Ratio
ef = EfficientFrontier(returns_stocks_mean, cov_matrix)
sharpe_weights = ef.max_sharpe(
risk_free_rate=Rf[0]
) # Para encontrar el portafolio tangencial
cleaned_weights = ef.clean_weights() # Para aproximar las cifras
print("Portafolio óptimo Sharpe:")
for stock, weight in cleaned_weights.items():
print(f"{stock}: {weight:.2%}")
# Mostrar la performance del portafolio óptimo
performance = ef.portfolio_performance(verbose=True, risk_free_rate=Rf[0])
Portafolio óptimo Sharpe:
FDX: 0.00%
KO: 0.00%
TSLA: 23.51%
WMT: 76.49%
Expected annual return: 2.8%
Annual volatility: 7.5%
Sharpe Ratio: 0.35
# Portafolio de Mínima Varianza:
ef_min = EfficientFrontier(returns_stocks_mean, cov_matrix)
min_weights = ef_min.min_volatility()
min_weights = ef_min.clean_weights()
# Extraer métricas del portafolio de mínima varianza
ret_min, vol_min, sharpe_min = ef_min.portfolio_performance(
risk_free_rate=Rf[0], verbose=True)
print("Portafolio de Mínima Varianza:")
for stock, weight in min_weights.items():
print(f"{stock}: {weight:.2%}")
Expected annual return: 1.0%
Annual volatility: 4.5%
Sharpe Ratio: 0.18
Portafolio de Mínima Varianza:
FDX: 0.13%
KO: 52.87%
TSLA: 0.00%
WMT: 47.00%
plt.figure(figsize=(10, 6))
# Crear una nueva instancia de EfficientFrontier para graficar la frontera
ef_plot = EfficientFrontier(returns_stocks_mean, cov_matrix)
plotting.plot_efficient_frontier(ef_plot, points=100, risk_free_rate=Rf[0])
# Graficar cada acción individualmente
for stock in stocks:
plt.scatter(volatility[stock], returns_stocks_mean[stock], label=stock)
plt.annotate(
stock,
(volatility[stock], returns_stocks_mean[stock]),
textcoords="offset points",
xytext=(0, 10),
ha="center",
)
# Agregar el portafolio de Sharpe
plt.scatter(
performance[1],
performance[0],
marker="*",
color="r",
s=100,
label="Portafolio Sharpe",
)
# Agregar el portafolio de mínima varianza (marcador "X" azul)
plt.scatter(
vol_min, ret_min, marker="X", color="b", s=100, label="Portafolio Min. Varianza"
)
plt.title("Frontera Eficiente")
plt.xlabel("Volatilidad")
plt.ylabel("Rendimiento esperado")
plt.legend()
plt.grid(True)
plt.show()