Conformación portafolio de inversión

Importar datos.

datos = read.csv("Cuatro acciones 2020.csv", sep=";", dec=",", header = T)

Matriz de precios.

precios = datos[,-1]

nombres = colnames(precios)
nombres
  1. 'ECO'
  2. 'PFVAVAL'
  3. 'ISA'
  4. 'NUTRESA'
acciones = ncol(precios)
acciones
4
precios = ts(precios)

Matriz de rendimientos.

rendimientos = diff(log(precios))

Coeficientes de correlación

correlacion = cor(rendimientos)
correlacion
A matrix: 4 × 4 of type dbl
ECOPFVAVALISANUTRESA
ECO1.00000000.65131610.15313170.3337626
PFVAVAL0.65131611.00000000.23085010.3305836
ISA0.15313170.23085011.00000000.4572004
NUTRESA0.33376260.33058360.45720041.0000000

Rendimientos esperado de cada acción.

rendimientos_esperados = apply(rendimientos, 2, mean)
rendimientos_esperados
ECO
-0.000447181465559539
PFVAVAL
-0.000398326704447035
ISA
0.000639854532799824
NUTRESA
-0.000268043266851791

Gráfico comparación rendimientos esperados de las acciones

barplot(rendimientos_esperados, horiz = T, main="Rendimientos esperados de las acciones")
../../_images/output_15_02.png

Volatilidad de cada acción.

volatilidades = apply(rendimientos, 2, sd)
volatilidades
ECO
0.0319324424190137
PFVAVAL
0.0285577211893029
ISA
0.0237292026947701
NUTRESA
0.0140104740592151

Gráfico comparación volatilidades de las acciones

barplot(volatilidades,horiz = T, main="Volatilidades de las acciones")
../../_images/output_19_04.png

Portafolio N° 1

Los portafolios de inversión se conforman con la compra de acciones. Los inversionistas invierten su dinero en adquirir cierta cantidad de acciones. Se tendrá el supuesto que sólo se realizan operaciones de compra y no operaciones de venta en corto.

Para determinar la composición exacta del portafolio de inversión se debe multiplicar la cantidad de acciones compradas por el último precio de mercado.

El número de acciones por cada activo financiera está representado por el vector numero_acciones y el último precio de mercado por s. La letra viene del nombre precio spot. Para determinar el valor de mercado de cada una de las acciones se hará la multiplicación: numero_acciones*s, lo cual se llamará valor_mercado_acciones.

De esta manera, el valor de mercado del portafolio, valor_portafolio, será la suma del valor de mercado de cada una de las acciones. Por último, la conformación del portafolio de inversión estará representada por las proporciones de inversión que tenga cada una de las acciones.

Último precio de las acciones

s = tail(precios, 1)
s = as.numeric(s)
s
  1. 2220
  2. 955
  3. 18000
  4. 22500

La acción de ECO tiene un precio 2.220 COP, PFAVAL de 955 COP, ISA de 18.000 COP y NUTRESA de 22.500 COP.

Número de acciones portafolio N° 1

Supongamos que se en el portafolio de inversión se realizaron las siguientes compras:

ECO: 150.000 acciones.

PFAVAL: 300.000 acciones.

ISA: 40.000 acciones.

NUTRESA: 70.000 acciones.

numero_acciones = c(150000,300000,40000,70000)
numero_acciones
  1. 150000
  2. 3e+05
  3. 40000
  4. 70000

Valor de mercado de las acciones portafolio N° 1

valor_mercado_acciones = numero_acciones*s
valor_mercado_acciones
  1. 3.33e+08
  2. 286500000
  3. 7.2e+08
  4. 1.575e+09

Lo invertido en ECO tiene un valor de 333.000.000 COP, en PFAVAL de 286.500.000 COP, en ISA de 720.000.000 COP y NUTRESA de 157.500.000

Valor de mercado portafolio de inversión portafolio N° 1

valor_portafolio = sum(valor_mercado_acciones)
valor_portafolio
2914500000

El portafolio de inversión tiene un valor de mercado de 2.914.500.000 COP.

Proporciones de inversión portafolio N° 1

proporciones = valor_mercado_acciones/valor_portafolio
proporciones
  1. 0.114256304683479
  2. 0.0983015954709213
  3. 0.24704065877509
  4. 0.540401441070509

La conformación del portafolio de inversión es la siguiente, aproximadamente:

ECO: 11,43%

PFAVAL: 9,83%

ISA: 24,70%

NUTRESA: 54,04%

La suma de las proporciones de inversión debe dar 100% porque se tiene el supuesto que se invierte todo el dinero disponible y no se realizan ventas en corto. Con las ventas en corto el porcentaje sería más del 100% porque se estaría apalancado.

sum(proporciones)
1
\[\sum_{i=1}^n w_i=1\]

Gráfica de proporciones de inversión portafolio N° 1

pie(proporciones, nombres, main="Proporciones de inversión portafolio N° 1", col=c("darkgreen","darkblue","darkgray","darkred"))
../../_images/output_41_02.png

Rendimientos del portafolio de inversión N° 1

El rendimiento del portafolio de inversión es el promedio ponderado de cada uno de los rendimientos de las acciones por los porcentajes de las proporciones de inversión.

\[R_P=\sum_{i=1}^nw_iR_i\]
rendimientos_portafolio = vector()

for(i in 1:nrow(rendimientos)){

  rendimientos_portafolio[i] = sum(rendimientos[i,]*proporciones)

}

head(rendimientos_portafolio, 10)
  1. -0.00674979626464658
  2. 0.00989168735951183
  3. 0.00382908516429467
  4. 0.00690563441971709
  5. -0.00182090582806878
  6. 0.0161071689440197
  7. 0.00338501947733235
  8. 0.014328020875826
  9. 0.00356937173801299
  10. 0.0071767045753624

Rendimiento esperado del portafolio de inversión N° 1

rendimiento_esperado_portafolio = mean(rendimientos_portafolio)
rendimiento_esperado_portafolio
-7.70303347164522e-05

El rendimiento esperado del portafolio de inversión es de -0,00007703% diario.

Volatilidad del portafolio de inversión portafolio N° 1

volatilidad_portafolio = sd(rendimientos_portafolio)
volatilidad_portafolio
0.0146098313397769

La volatilidad del portafolio de inversión es de 1,46% diaria.

Gráfico comparación rendimientos esperados con portafolio N° 1

barplot(c(rendimientos_esperados, rendimiento_esperado_portafolio), horiz = T, main = "Rendimientos esperados de las acciones\n y del portafolio de inversión N° 1")
../../_images/output_54_02.png

Gráfico comparación volatilidades con portafolio N° 1

barplot(c(volatilidades,volatilidad_portafolio), horiz = T, main = "Volatilidades de las acciones\n y del portafolio de inversión N° 1")
../../_images/output_56_0.png

Portafolio N° 2

Por practicidad, se hace análisis de los portafolios de inversión a partir de las proporciones de inversión sin tener en cuenta la cantidad de acciones en cada activo. Esto se hace como una aproximación a los porcentajes de inversión reales.

proporciones = c(0.20,0.30,0.15,0.35)
proporciones
  1. 0.2
  2. 0.3
  3. 0.15
  4. 0.35
sum(proporciones)
1

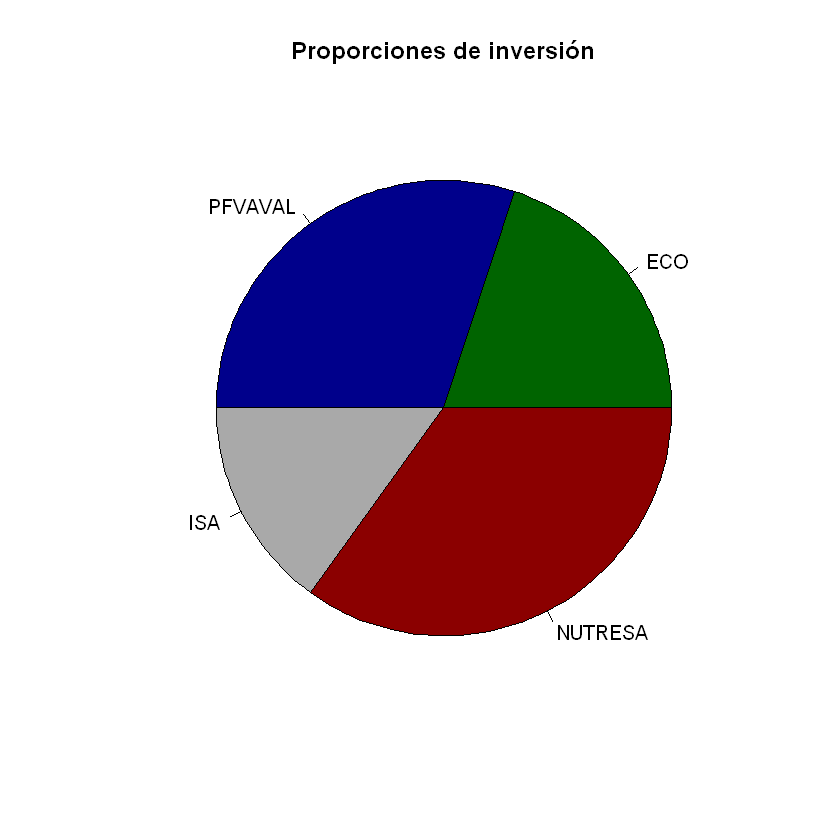
Gráfica de proporciones de inversión portafolio N° 2

pie(proporciones, nombres, main="Proporciones de inversión", col = c("darkgreen","darkblue","darkgray","darkred"))
../../_images/output_62_01.png

Rendimientos del portafolio de inversión portafolio N° 2

rendimientos_portafolio=vector()

for(i in 1:nrow(rendimientos)){

  rendimientos_portafolio[i] = sum(rendimientos[i,]*proporciones)

}

Rendimiento esperado del portafolio de inversión N° 2

rendimiento_esperado_portafolio = mean(rendimientos_portafolio)
rendimiento_esperado_portafolio
-0.000206771267924171

El rendimiento esperado del portafolio de inversión es de -0,0207% diario.

Volatilidad del portafolio de inversión portafolio N° 1

volatilidad_portafolio = sd(rendimientos_portafolio)
volatilidad_portafolio
0.0175458696925969

La volatilidad del portafolio de inversión es de 1,75% diaria.

Gráfico comparación rendimientos esperados con portafolio N° 2

barplot(c(rendimientos_esperados,rendimiento_esperado_portafolio), horiz = T, main="Rendimientos esperados de las acciones\n y del portafolio de inversión N° 2")
../../_images/output_72_02.png

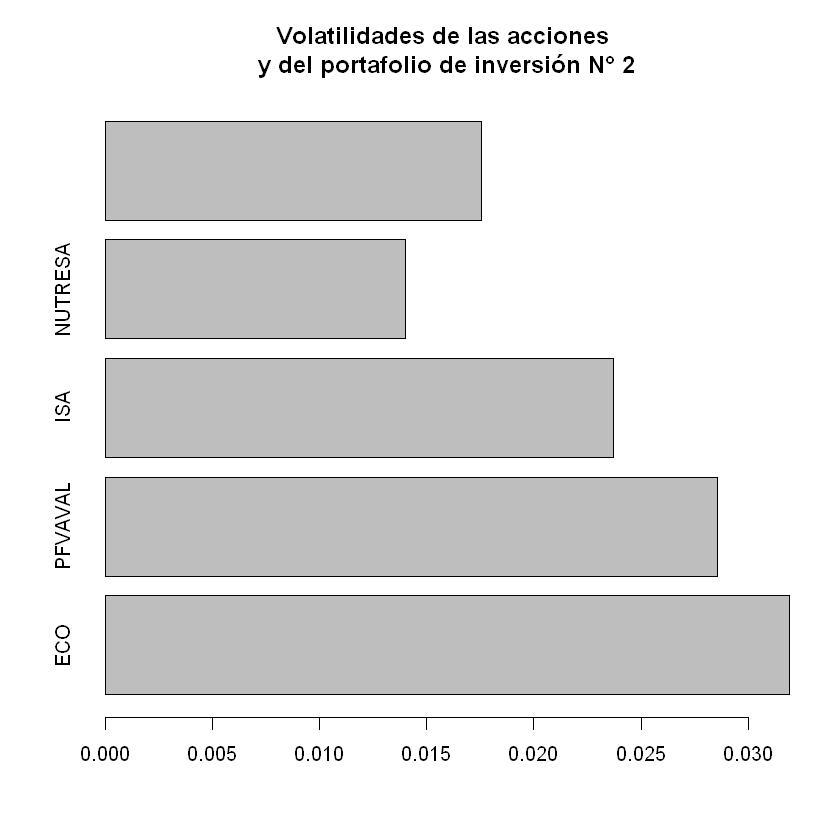
Gráfico comparación volatilidades con portafolio N° 2

barplot(c(volatilidades,volatilidad_portafolio), horiz = T, main="Volatilidades de las acciones\n y del portafolio de inversión N° 2")
../../_images/output_74_0.png