Ejercicio reducción de dimensionalidad#

Encuesta Anual Manufacturera – EAM - 2021:#

Datos del DANE: Encuesta Anual Manufacturera – EAM - 2021

Variables:#

  • c4r4c9t: Personal ocupado mujeres

  • c4r4c10t: Personal ocupado hombres

  • c3r10c3: Costos y gastos en personal

  • c3r31c2: Intereses préstamos

  • c3r35c3: Total costos y gastos

  • c5r1c4: Consumo energía

  • c7r10c2: Inversiones en Activos Fijos

  • ACTIVFI: Activos Fijos

  • VALORVEN: Ventas

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA

# Cargar el archivo Excel
data = pd.read_excel("EAM_ANONIMIZADA_2021.xlsx")

# Definir un diccionario que mapea los nombres de las columnas originales a los nuevos nombres
columns_mapping = {
    "c4r4c9t": "Personal ocupado mujeres",
    "c4r4c10t": "Personal ocupado hombres",
    "c3r10c3": "Costos y gastos en personal",
    "c3r31c2": "Intereses préstamos",
    "c3r35c3": "Total costos y gastos",
    "c5r1c4": "Consumo energía",
    "c7r10c2": "Inversiones en Activos Fijos",
    "ACTIVFI": "Activos Fijos",
    "VALORVEN": "Ventas",
}

# Seleccionar las columnas deseadas y renombrarlas usando el diccionario
df = data[list(columns_mapping.keys())].rename(columns=columns_mapping)

# Mostrar las primeras filas del dataframe extraído para confirmar la operación
df.head()
Personal ocupado mujeres Personal ocupado hombres Costos y gastos en personal Intereses préstamos Total costos y gastos Consumo energía Inversiones en Activos Fijos Activos Fijos Ventas
0 6 5 228676 0 80309 17376 0 85550 741558
1 133 20 5811645 1433181 14197654 1196407 3690937 20528507 45837888
2 20 7 554205 509 310002 181255 0 683547 1365834
3 14 20 791070 5167 5870197 27616 18091 18091 9456199
4 18 11 582746 50 2349122 72065 267544 449380 3239329 
# Verificar la existencia de valores NaN en el dataframe extraído
df.isna().sum()

Personal ocupado mujeres        0
Personal ocupado hombres        0
Costos y gastos en personal     0
Intereses préstamos             0
Total costos y gastos           0
Consumo energía                 0
Inversiones en Activos Fijos    0
Activos Fijos                   0
Ventas                          0
dtype: int64

Análisis de los datos:#

# Generar un análisis descriptivo de las variables extraídas
analysis = df.describe()

# Mostrar el análisis descriptivo
analysis
Personal ocupado mujeres Personal ocupado hombres Costos y gastos en personal Intereses préstamos Total costos y gastos Consumo energía Inversiones en Activos Fijos Activos Fijos Ventas
count 7138.000000 7138.000000 7.138000e+03 7.138000e+03 7.138000e+03 7.138000e+03 7.138000e+03 7.138000e+03 7.138000e+03
mean 33.745167 61.694172 4.155579e+06 4.932111e+05 1.409134e+07 2.333911e+06 2.145846e+06 3.108843e+07 4.500835e+07
std 71.751628 110.951738 1.104522e+07 5.805060e+06 8.136519e+07 1.397313e+07 1.942048e+07 3.076136e+08 1.893239e+08
min 0.000000 0.000000 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
25% 4.000000 8.000000 3.851698e+05 0.000000e+00 2.753795e+05 2.995825e+04 0.000000e+00 5.382692e+05 1.317152e+06
50% 11.000000 22.000000 1.051176e+06 2.096300e+04 1.123743e+06 1.217630e+05 3.148450e+04 2.168256e+06 4.563190e+06
75% 32.000000 64.000000 3.508761e+06 1.486320e+05 5.471251e+06 7.007225e+05 5.622830e+05 1.056892e+07 2.251448e+07
max 1322.000000 1507.000000 3.859138e+08 2.987014e+08 2.406595e+09 4.235338e+08 7.868389e+08 1.325022e+10 5.610902e+09 
# Calcular la matriz de correlación
correlation_matrix = df.corr()

# Crear un heatmap de la matriz de correlación usando seaborn
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, fmt=".2f", cmap="coolwarm", cbar=True)
plt.title("Matriz de Correlación de las Variables Extraídas")
plt.show()
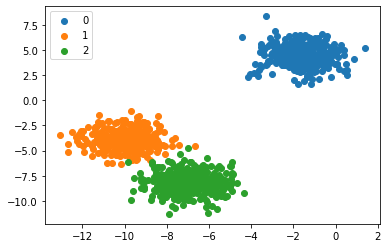
../../../_images/output_10_03.png 
# Pairplot
sns.pairplot(df)
plt.suptitle("Pairplot", y=1.02)
plt.show()
../../../_images/output_11_03.png

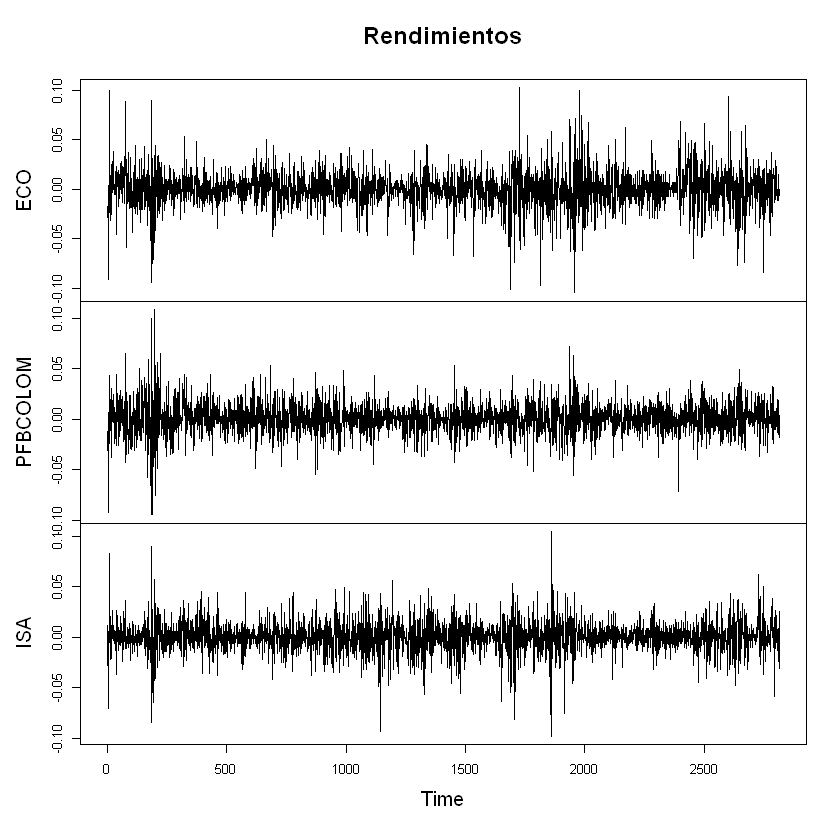
Datos atípicos:#

# Función para eliminar los outliers usando el método IQR
def remove_outliers(df):
    Q1 = df.quantile(0.25)
    Q3 = df.quantile(0.75)
    IQR = Q3 - Q1
    lower_bound = Q1 - 1.5 * IQR
    upper_bound = Q3 + 1.5 * IQR
    return df[~((df < lower_bound) | (df > upper_bound)).any(axis=1)]


# Eliminar los outliers
cleaned_df = remove_outliers(df)
print(f"Se eliminaron {len(df) - len(cleaned_df)} filas con outliers.")
print(f"El nuevo tamaño del dataframe es: {cleaned_df.shape}")

Se eliminaron 2247 filas con outliers.
El nuevo tamaño del dataframe es: (4891, 9)

# Calcular la matriz de correlación
correlation_matrix = cleaned_df.corr()

# Crear un heatmap de la matriz de correlación usando seaborn
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, fmt=".2f", cmap="coolwarm", cbar=True)
plt.title("Matriz de Correlación de las Variables Extraídas")
plt.show()
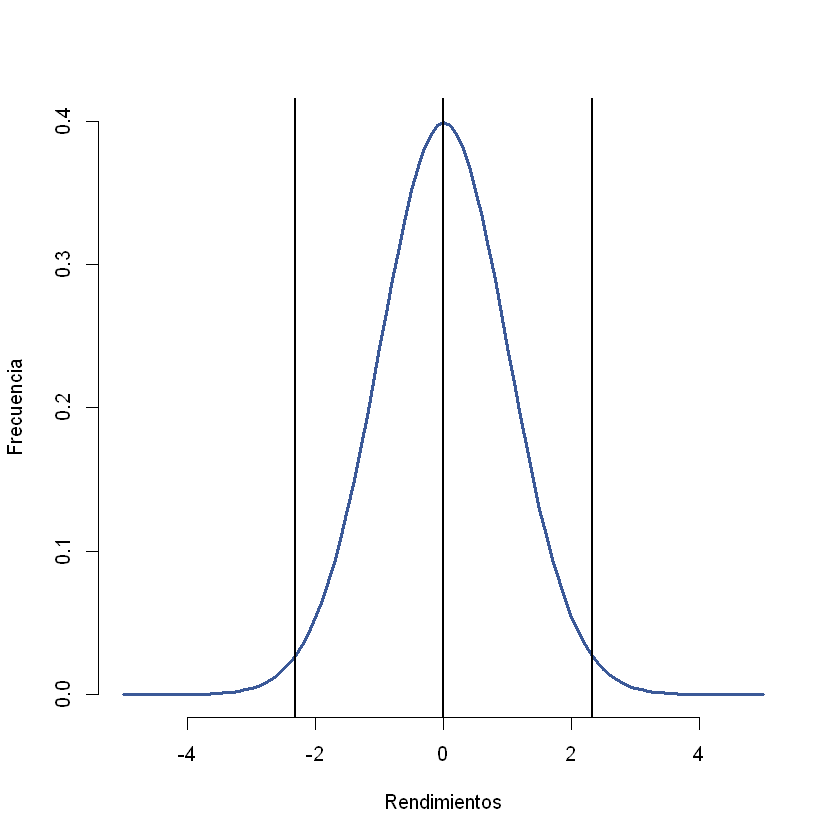
../../../_images/output_14_02.png 
# Pairplot
sns.pairplot(cleaned_df)
plt.suptitle("Pairplot", y=1.02)
plt.show()
../../../_images/output_15_03.png

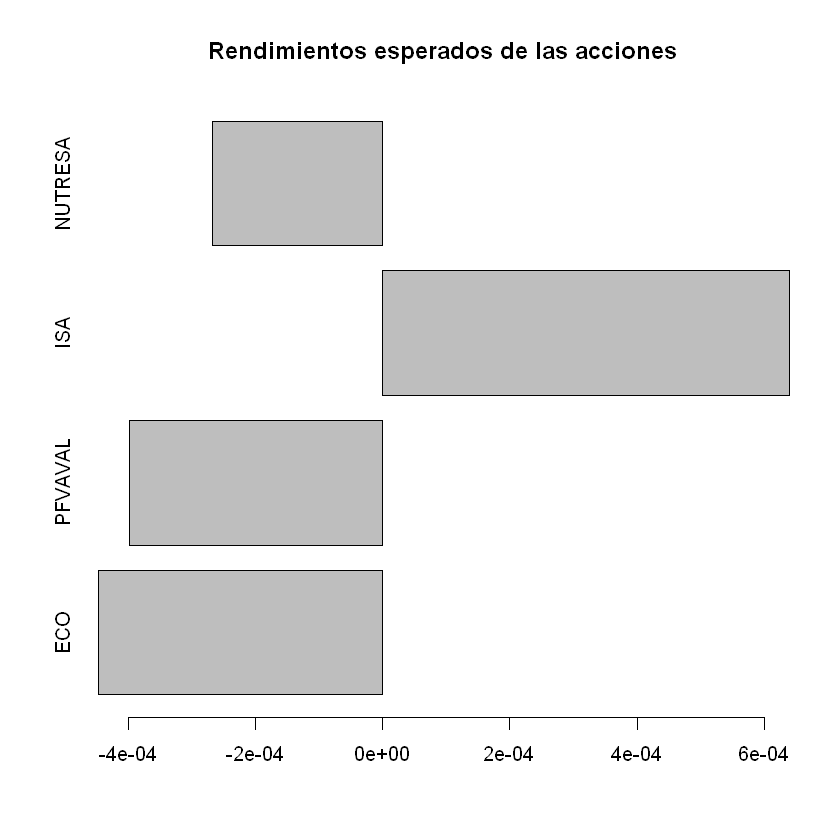
Estandarización de variables:#

scaler = StandardScaler()
scaled_data = scaler.fit_transform(cleaned_df)

scaled_data.shape[1]

9

PCA:#

# Aplicación de PCA estándar
pca = PCA()
pca.fit(scaled_data)

# Cálculo de las varianzas explicadas
explained_variance = pca.explained_variance_ratio_

print("Varianza explicada por cada componente principal:")
print(explained_variance)

# Cálculo de la varianza explicada acumulada
explained_variance_cum = np.cumsum(pca.explained_variance_ratio_)

# Visualización del gráfico de varianza explicada
plt.figure(figsize=(8, 6))
plt.plot(
    range(1, len(explained_variance_cum) + 1),
    explained_variance_cum,
    marker="o",
    linestyle="--",
)
plt.xlabel("Número de Componentes Principales")
plt.ylabel("Varianza Explicada Acumulada")
plt.title("Gráfico de Varianza Explicada Acumulada")
plt.grid()
plt.show()

Varianza explicada por cada componente principal:
[0.52251946 0.09461587 0.082243   0.07885179 0.06430531 0.05538482
 0.04890064 0.0406377  0.01254142]
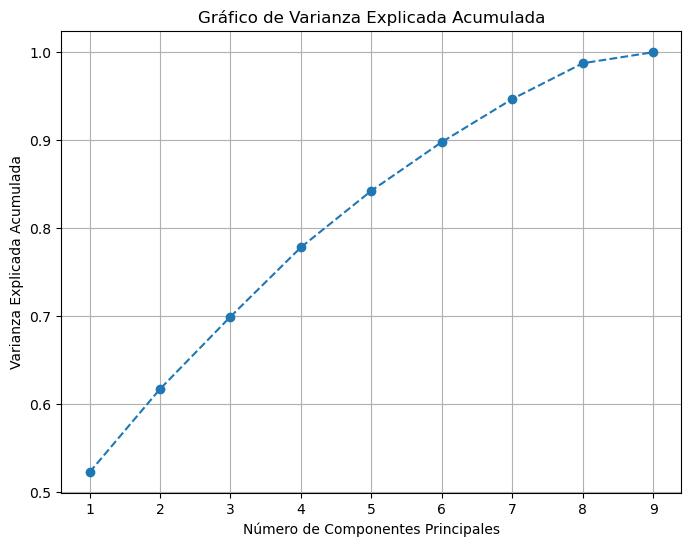
../../../_images/output_20_12.png

Con 4 Componentes Principales, varianza explicada:

explained_variance_cum[3]

0.778230124161743

Con 4 Componentes se logra explicar el 77,8% de la varianza total.

# Aplicación de PCA estándar
num_components = 4
pca = PCA(n_components=num_components)
X_pca = pca.fit_transform(scaled_data)

# Obtener las cargas de las variables originales (matriz de rotación)
rotation_matrix = pd.DataFrame(
    pca.components_.T,
    columns=[f"PC{i+1}" for i in range(num_components)],
    index=cleaned_df.columns,
)

# Mostrar la matriz de rotación
print(rotation_matrix)

                                   PC1       PC2       PC3       PC4
Personal ocupado mujeres      0.288507 -0.589885 -0.206510  0.401413
Personal ocupado hombres      0.383266  0.103472 -0.233956 -0.041429
Costos y gastos en personal   0.412412 -0.158810 -0.191314  0.159284
Intereses préstamos           0.263162 -0.433097  0.339110 -0.741836
Total costos y gastos         0.348081 -0.137960  0.156678  0.027073
Consumo energía               0.305263  0.457126 -0.414624 -0.214545
Inversiones en Activos Fijos  0.270031  0.261610  0.728942  0.406090
Activos Fijos                 0.330204  0.353372  0.130284 -0.194323
Ventas                        0.366382  0.085015 -0.078930  0.109665

# Cantidad de empresas y Componentes Principales
X_pca.shape

(4891, 4)

# Convert X_pca to a pandas DataFrame
X_pca_df = pd.DataFrame(X_pca)

# Calculate the correlation matrix
correlation_matrix = X_pca_df.corr()

# Create a heatmap of the correlation matrix using seaborn
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, fmt=".2f", cmap="coolwarm", cbar=True)
plt.title("Matriz de Correlación de las Variables Extraídas")
plt.show()
../../../_images/output_27_01.png 
# Obtener las cargas de las variables originales
loadings = pca.components_.T * np.sqrt(pca.explained_variance_)

# Función para crear el biplot
def biplot(score, coeff, pc_x=0, pc_y=1, labels=None, ax=None):
    xs = score[:, pc_x]
    ys = score[:, pc_y]
    n = coeff.shape[0]
    scalex = 1.0 / (xs.max() - xs.min())
    scaley = 1.0 / (ys.max() - ys.min())
    ax.scatter(xs * scalex, ys * scaley, c="blue")
    for i in range(n):
        ax.arrow(0, 0, coeff[i, pc_x], coeff[i, pc_y], color="r", alpha=0.5)
        if labels is None:
            ax.text(
                coeff[i, pc_x] * 1.15,
                coeff[i, pc_y] * 1.15,
                "Var" + str(i + 1),
                color="g",
                ha="center",
                va="center",
            )
        else:
            ax.text(
                coeff[i, pc_x] * 1.15,
                coeff[i, pc_y] * 1.15,
                labels[i],
                color="g",
                ha="center",
                va="center",
            )

    ax.set_xlabel(f"Componente Principal {pc_x+1}")
    ax.set_ylabel(f"Componente Principal {pc_y+1}")
    ax.grid()


# Crear subplots para cada par de componentes principales
combinations = [
    (i, j) for i in range(num_components) for j in range(i + 1, num_components)
]
num_plots = len(combinations)
cols = 2
rows = (num_plots // cols) + (num_plots % cols)

fig, axs = plt.subplots(rows, cols, figsize=(20, rows * 10 / cols))

for ax, (pc_x, pc_y) in zip(axs.flatten(), combinations):
    biplot(X_pca, loadings, pc_x, pc_y, list(cleaned_df.columns), ax=ax)
    ax.set_title(f"Biplot de las Componentes Principales {pc_x+1} vs {pc_y+1}")

# Eliminar subplots vacíos si hay
if num_plots % cols != 0:
    for i in range(num_plots, rows * cols):
        fig.delaxes(axs.flatten()[i])

plt.tight_layout()
plt.show()
../../../_images/output_28_0.png

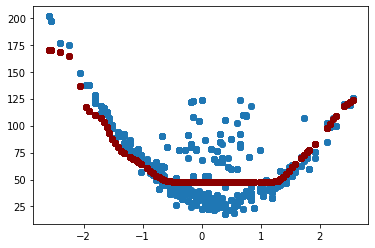
Análisis:#

Las variables con las mayores cargas en PC1, ordenadas de mayor a menor, son:

  • Costos y gastos en personal.

  • Personal ocupado hombres.

  • Ventas.

En el primer biplot, estas tres variables muestran el mayor desplazamiento en el eje PC1.

Las tres variables con las cargas más bajas en PC1 son Personal ocupado mujeres, Inversiones en Activos Fijos e Intereses préstamos. En el Biplot, estas variables se representan con el menor desplazamiento horizontal.

Para PC2, se deben observar los desplazamientos verticales. Las variables con las mayores cargas en valor absoluto son Personal ocupado mujeres e Intereses préstamos, ambas con cargas negativas. Esto se refleja en el primer Biplot como un desplazamiento hacia abajo.

PC1 está positivamente correlacionado con todas las variables, ya que todas tienen una carga positiva.

Estos puntos también se pueden analizar utilizando la matriz de rotación.

# Mostrar la matriz de rotación
print(rotation_matrix)

                                   PC1       PC2       PC3       PC4
Personal ocupado mujeres      0.288507 -0.589885 -0.206510  0.401413
Personal ocupado hombres      0.383266  0.103472 -0.233956 -0.041429
Costos y gastos en personal   0.412412 -0.158810 -0.191314  0.159284
Intereses préstamos           0.263162 -0.433097  0.339110 -0.741836
Total costos y gastos         0.348081 -0.137960  0.156678  0.027073
Consumo energía               0.305263  0.457126 -0.414624 -0.214545
Inversiones en Activos Fijos  0.270031  0.261610  0.728942  0.406090
Activos Fijos                 0.330204  0.353372  0.130284 -0.194323
Ventas                        0.366382  0.085015 -0.078930  0.109665