Optimizadores#
Keras tiene varios algoritmos para optimizar el entrenamiento de la red neuronal artificial aquí.
optimizer =: por defecto usa "rmsprop".
Los algoritmos son: "sgd", "rmsprop", "adam", "AdamW",
"Adadelta", "Adagrad", "Adamax", entre otros.
Esto métodos se aplican al Gradiente Descendente y tienen diferentes maneras de optimizar los parámetros de la red neuronal.
Gradiente Descendente Estocástico#
keras.optimizers.SGD(
learning_rate=0.01,
momentum=0.0,
nesterov=False,
)
El descenso del gradiente estocástico es una técnica para entrenar modelos ajustando los pesos paso a paso con el fin de minimizar el error.
A diferencia del descenso del gradiente clásico, que usa todos los datos para calcular el gradiente, el método estocástico utiliza solo un ejemplo o un pequeño conjunto de ejemplos (mini-batch) en cada iteración.
Esto hace que el aprendizaje sea más rápido, aunque un poco más ruidoso, lo que puede ayudar a escapar de mínimos locales y encontrar mejores soluciones.
Intuición:
Cada paso del SGD es como dar pasos cortos cuesta abajo en una montaña, pero viendo solo una parte del terreno.
Aunque el camino es ruidoso, normalmente se llega al valle (mínimo) mucho más rápido.
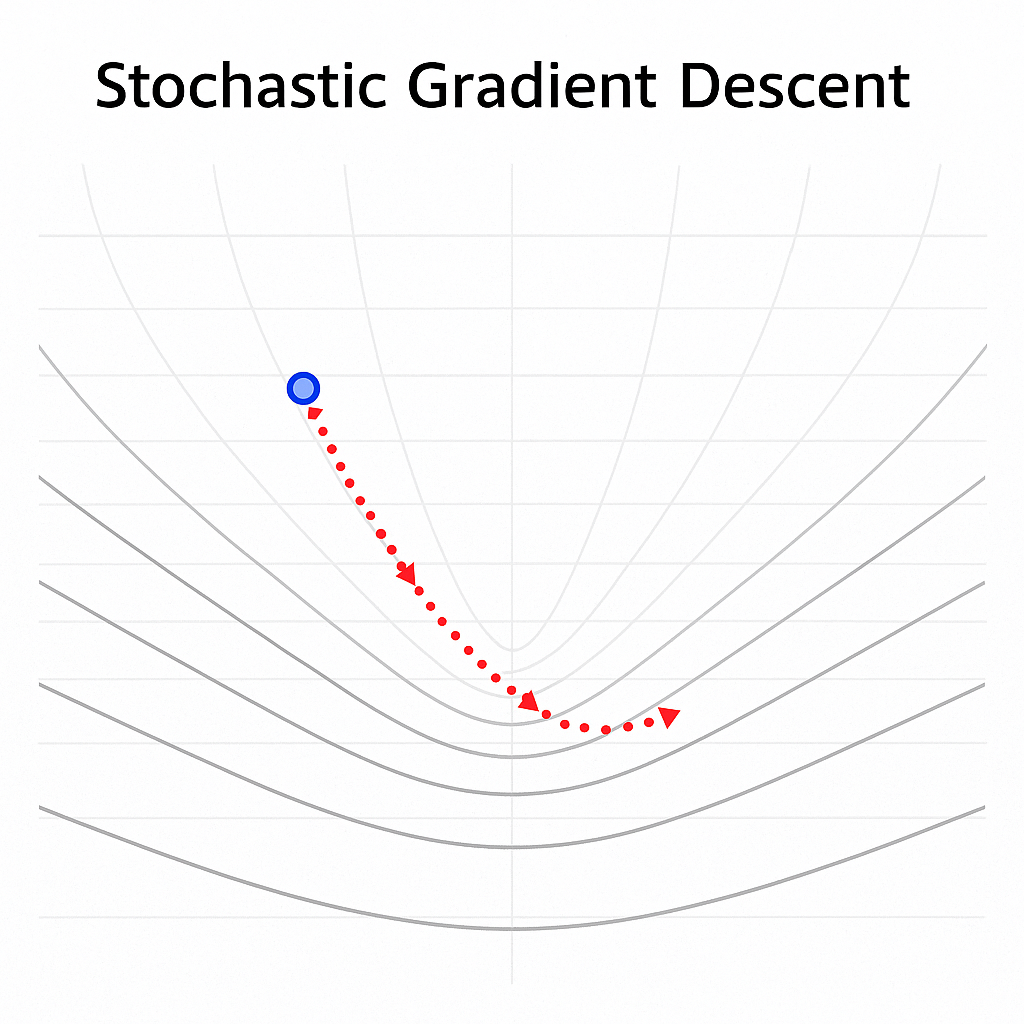
SGD#
Gradiente Descendente Estocástico con Momentum (SGD + Momentum)
El SGD con momentum mejora el descenso del gradiente estocástico al agregar una “inercia” o memoria del movimiento anterior.
La idea es que, en lugar de mover los pesos solo en función del gradiente actual, se tenga en cuenta también la dirección acumulada de los gradientes previos.
Esto permite que el aprendizaje sea más estable y rápido, especialmente cuando la superficie de error tiene muchas oscilaciones.
Ecuaciones:
\(v^{(nextStep)} = \mu \times v - \eta \times \frac{\partial}{\partial W} MSE(W)\)
\(W^{(nextStep)} = W + v^{(nextStep)}\)
donde:
\(\eta\) es la tasa de aprendizaje (learning rate).
\(\mu\) es el factor de momentum (por ejemplo, 0.9).
\(v\) es la “velocidad” acumulada del gradiente.
Intuición:
El momentum actúa como una bola rodando cuesta abajo: mantiene velocidad en direcciones consistentes y suaviza los cambios bruscos, ayudando a llegar al mínimo más rápido y con menos oscilaciones.
Momentum:
Momentum#
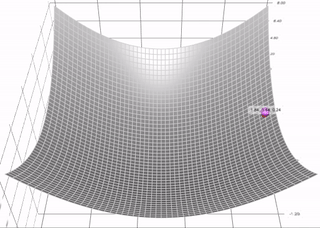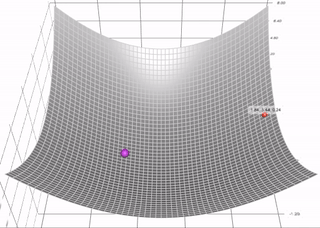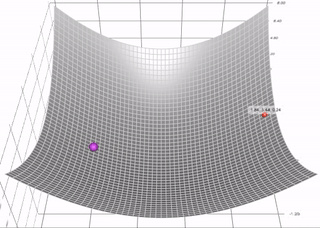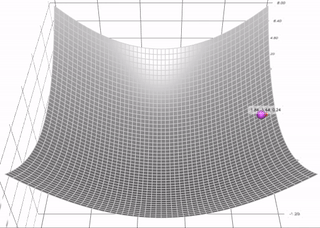
El método del Descenso del Gradiente estándar realiza pasos pequeños y regulares por la pendiente de la función de costo, por lo que el algoritmo tarda en llegar al fondo de la función, en cambio, Momentum realiza una aceleración para llegar al fondo de la función más rápido, es decir, comienza lentamente, pero rápidamente toma impulso hasta que finalmente alcanza cierta velocidad.
El método del Descenso del Gradiente tradicional no considera los gradientes anteriores, si el gradiente local es pequeño, va muy lentamente, en cambio, Momentum sí tiene en cuenta los gradientes anteriores en cada iteración, en otras palabras, el gradiente se usa para la aceleración, no para la velocidad.
El algoritmo introduce un nuevo hiperparámetro \(\mu\) llamado momentum, que por defecto se establece en 0 indicando alta fricción (como la fricción de una superficie) y 1 para sin fricción, un valor de momentum de 0,9 es bueno.
Este impulso en el Descenso del Gradiente permite que Momentum escape de las mesetas mucho más rápido que el Descenso del Gradiente.
Cuando las entradas a la red neuronal tienen escalas diferentes, la función de costo tendrá la forma de un tazón alargado. En esta forma el Descenso del Gradiente descenderá rápido por la pendiente empinada, pero luego se volverá lento al descender por el valle. Por el contrario, Momentum rodará por el valle cada vez más rápido hasta llegar al fondo que el óptimo.
Las capas superiores de las redes neuronales profundan a menudo terminan teniendo entradas con escalas diferentes, por lo que usar Optimización Momentum ayuda mucho.
Este optimizador también ayuda a superar los óptimos locales.
El único inconveniente de la Momentum es que agrega otro hiperparámetro para ajustar. Sin embargo, el valor de momentum de \(0,9\) suele funcionar bien en la práctica y casi siempre va más rápido que el descenso de gradiente normal.
nesterov:
SGD(learning_rate=0.01, momentum=0.9, nesterov=True)
Esto activa el llamado Nesterov momentum (Nesterov Accelerated Gradient).
La idea intuitiva que puedes enseñar es:
El momentum clásico mira el gradiente en la posición actual.
Nesterov es un poquito más “listo”: antes de calcular el gradiente, “predice” hacia dónde estaría el peso si aplicara la velocidad, y evalúa el gradiente allí.
Dicho de otra forma:
Te adelantas con tu inercia.
Calculas el gradiente en esa posición adelantada.
Usas ese gradiente corregido para decidir el ajuste.
RMSProp#
keras.optimizers.RMSprop(
learning_rate=0.001,
rho=0.9,
momentum=0.0,
epsilon=1e-07,
)
RMSProp (Root Mean Square Propagation) es un optimizador que ajusta automáticamente la tasa de aprendizaje para cada peso del modelo, dependiendo de la magnitud reciente de sus gradientes.
El RMSProp con momentum combina dos ideas:
Ajusta automáticamente la tasa de aprendizaje para cada peso (RMSProp).
Añade un componente de inercia que acumula la dirección de los gradientes (momentum).
Esto permite que el entrenamiento sea más rápido y estable, evitando oscilaciones cuando los gradientes son grandes y acelerando cuando son pequeños.
En palabras sencillas:
Si un peso tiene gradientes grandes → se le da un paso más pequeño.
Si un peso tiene gradientes pequeños → se le da un paso más grande.
Esto evita que el entrenamiento “salte” o “explote” cuando algunos parámetros tienen gradientes mucho más grandes que otros.
Ecuaciones:
\(S^{(nextStep)} = \rho \times S + (1 - \rho) \times \left( \frac{\partial}{\partial W} MSE(W) \right)^2\)
\(v^{(nextStep)} = \mu \times v - \frac{\eta}{\sqrt{S^{(nextStep)} + \varepsilon}} \times \frac{\partial}{\partial W} MSE(W)\)
\(W^{(nextStep)} = W + v^{(nextStep)}\)
donde:
\(\eta\) es la tasa de aprendizaje (learning rate).
\(\rho\) controla el promedio móvil de los gradientes al cuadrado (≈ 0.9).
\(\mu\) es el factor de momentum (≈ 0.9).
\(\varepsilon\) evita divisiones por cero (≈ 1e-7).
Intuición:
RMSProp ajusta el tamaño del paso según la magnitud de los gradientes recientes, mientras que el momentum suaviza la trayectoria, como una bola que rueda cuesta abajo con impulso.
Adam:#
keras.optimizers.Adam(
learning_rate=0.001,
beta_1=0.9,
beta_2=0.999,
epsilon=1e-07,
)
Adam con Momentum
El Adam (Adaptive Moment Estimation) es un optimizador que combina las ventajas del momentum y de RMSProp.
Utiliza dos promedios móviles:
Uno del gradiente (dirección promedio, como el momentum).
Otro del gradiente al cuadrado (magnitud promedio, como RMSProp).
Así, ajusta automáticamente la velocidad y la dirección del aprendizaje para cada peso, haciendo el entrenamiento más rápido y estable.
Ecuaciones:
\(m^{(nextStep)} = \beta_1 \times m + (1 - \beta_1) \times \frac{\partial}{\partial W} MSE(W)\)
\(v^{(nextStep)} = \beta_2 \times v + (1 - \beta_2) \times \left( \frac{\partial}{\partial W} MSE(W) \right)^2\)
\(\hat{m} = \frac{m^{(nextStep)}}{1 - \beta_1^t}\)
\(\hat{v} = \frac{v^{(nextStep)}}{1 - \beta_2^t}\)
\(W^{(nextStep)} = W - \frac{\eta}{\sqrt{\hat{v}} + \varepsilon} \times \hat{m}\)
donde:
\(\eta\) es la tasa de aprendizaje.
\(\beta_1\) y \(\beta_2\) controlan el promedio de los gradientes (≈ 0.9 y 0.999).
\(\varepsilon\) evita divisiones por cero (≈ 1e-7).
Intuición:
Otros optimizadores#
Los siguientes métodos son variaciones o extensiones del descenso del gradiente que buscan mejorar la velocidad y estabilidad del entrenamiento.
Cada uno ajusta de forma diferente la tasa de aprendizaje y la forma en que se actualizan los pesos.
Opt imizador |
Idea principal |
Ve ntajas |
Des ventajas |
Parámetros clave |
|---|---|---|---|---|
AdamW |
Variante de Adam que separa c orrectamente el weight decay (decaimiento de pesos) de la a ctualización del gradiente. |
Mejor regular ización, evita que los pesos crezcan de masiado. |
Requiere ajustar el valor de de caimiento. |
\(\eta\), :m ath:beta_1, :m ath:beta_2, :math: varepsilon, weight decay |
Adagrad* |
Ajusta aut omáticamente la tasa de aprendizaje dividiendo por la raíz de la suma acumulada de gradientes al cuadrado. |
Ideal para datos d ispersos ( sparse). |
El learning rate se vuelve muy pequeño con el tiempo. |
\(\eta\), :math :varepsilon |
** Adadelta** |
Extiende Adagrad limitando la acumulación del cuadrado de gradientes, usando una media móvil. |
No necesita tasa de apr endizaje inicial fija. |
Puede ser menos estable en redes profundas. |
\(\rho\), :math :varepsilon |
Adamax |
Variante de Adam que usa la norma infinito en lugar de la norma cuadrada de los gradientes. |
Más robusto frente a gr adientes grandes o r uidosos. |
Puede converger más lento que Adam. |
\(\eta\), :m ath:beta_1, :m ath:beta_2, :math :varepsilon |
Estos optimizadores adaptativos son variantes de Adam o Adagrad.
AdamW → mejora la regularización.
Adadelta → simplifica el ajuste de la tasa de aprendizaje.
Adagrad → útil para datos dispersos.
Adamax → versión estable de Adam ante gradientes extremos.
Momentum#
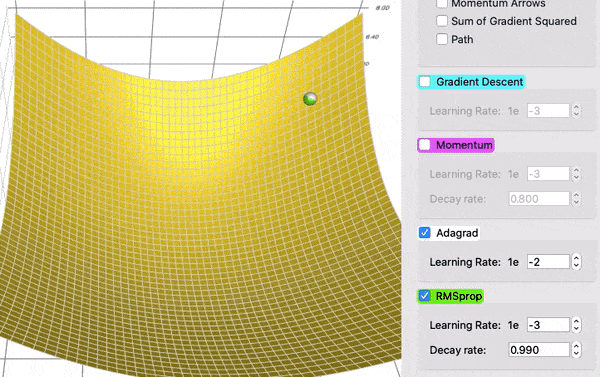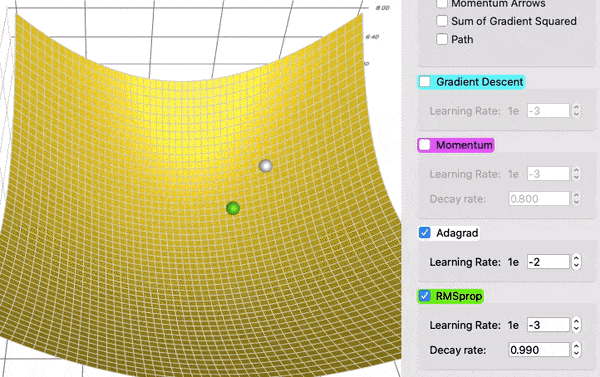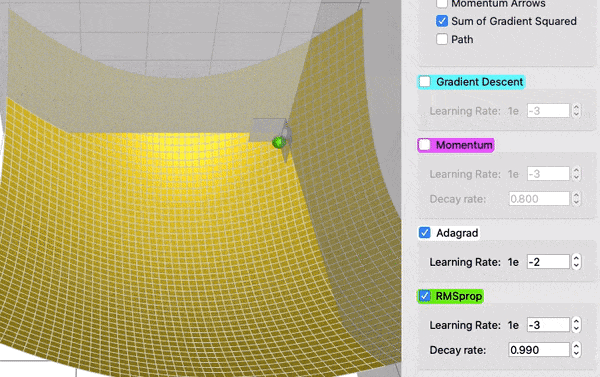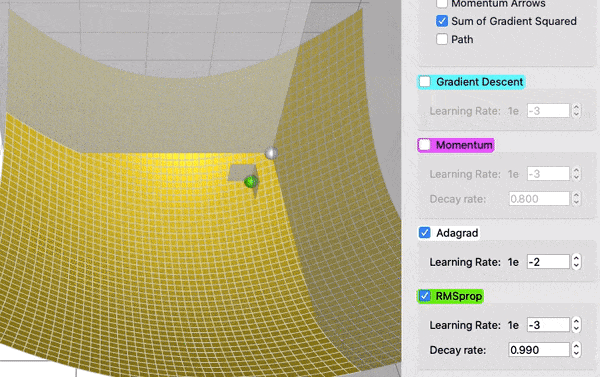
RMSProp#
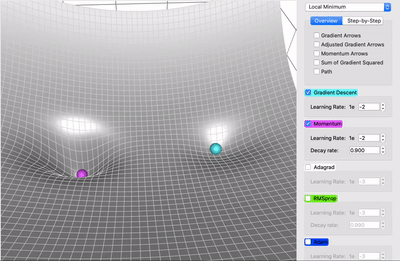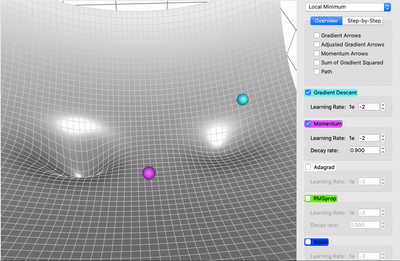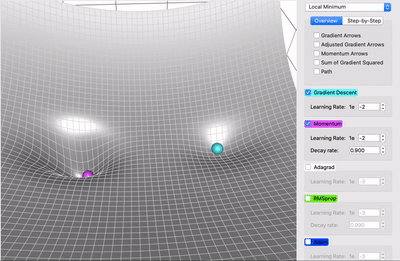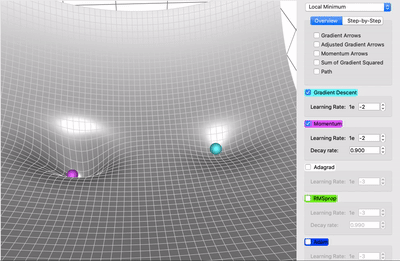
Optimizadores_3#
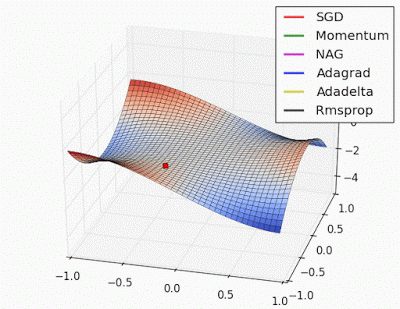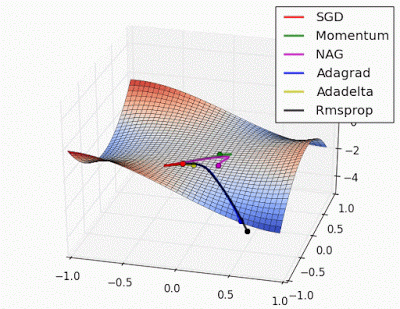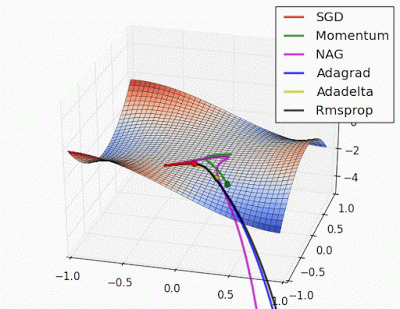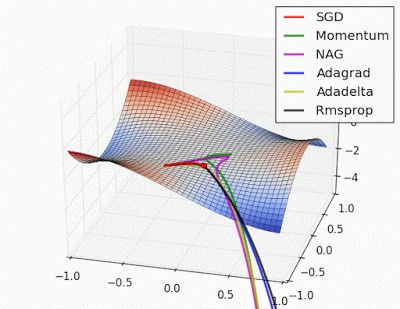
Optimizadores#
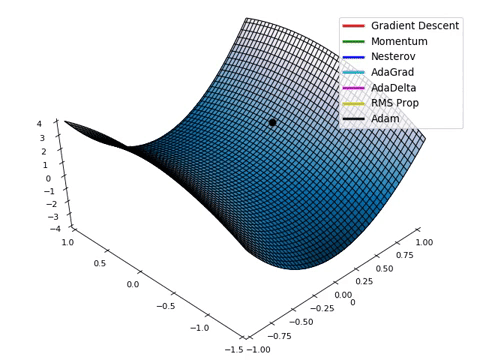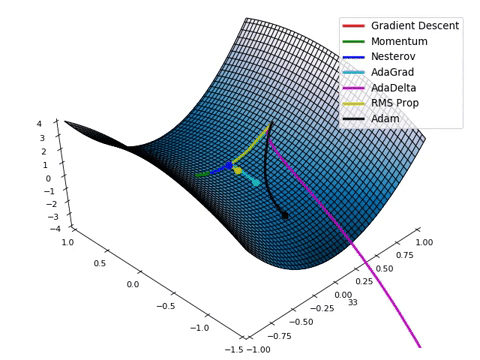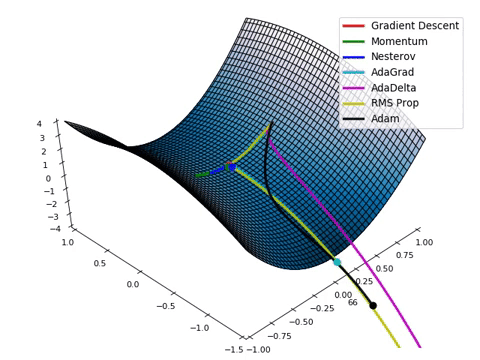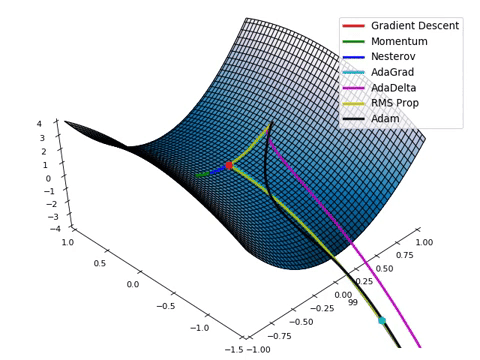
Optimizadores_2#