Ejercicio PCA - acciones

import yfinance as yf
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

Descargar precios de acciones con diferentes características.

acciones = [
    # 🟢 Acciones de bajo Beta (< 0.8) — defensivas
    'JNJ',   # Johnson & Johnson
    'PG',    # Procter & Gamble
    'KO',    # Coca-Cola
    'PEP',   # PepsiCo
    'WMT',   # Walmart

    # 🟡 Acciones de Beta cercano a 1 (≈ 0.9 - 1.1) — mercado promedio
    'AAPL',  # Apple
    'MSFT',  # Microsoft
    'V',     # Visa
    'MA',    # Mastercard
    'UNH',   # UnitedHealth

    # 🔴 Acciones de Beta alto (> 1.2) — más volátiles que el mercado
    'TSLA',  # Tesla
    'NVDA',  # Nvidia
    'META',  # Meta (Facebook)
    'AMZN',  # Amazon
    'NFLX',  # Netflix

    # 🔁 Adicionales mixtas para aumentar diversidad
    'GOOGL', # Alphabet (Google)
    'AMD',   # Advanced Micro Devices
    'CRM',   # Salesforce
    'BA',    # Boeing
    'NKE'    # Nike
]

indice = '^GSPC'  # S&P500

datos = yf.download(acciones + [indice], start='2020-07-01', end='2025-07-31', interval='1mo')['Close']
datos.dropna(inplace=True)

datos.describe()

/tmp/ipython-input-4028798923.py:33: FutureWarning: YF.download() has changed argument auto_adjust default to True
  datos = yf.download(acciones + [indice], start='2020-07-01', end='2025-07-31', interval='1mo')['Close']
[*******************100%*********************]  21 of 21 completed

Ticker	AAPL	AMD	AMZN	BA	CRM	GOOGL	JNJ	KO	MA	META	...	NFLX	NKE	NVDA	PEP	PG	TSLA	UNH	V	WMT	^GSPC
count	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000	...	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000	61.000000
mean	168.308615	111.604426	157.696810	192.557214	234.247294	130.157316	149.466882	56.029760	398.977761	351.281430	...	555.438689	106.611316	53.068235	149.308490	141.179571	246.167060	444.539696	241.869444	56.422426	4591.564901
std	37.929746	32.599924	35.406763	31.330118	48.640246	32.428267	10.006478	8.197990	82.631453	165.833288	...	256.862147	26.270569	47.606693	17.191153	16.928583	67.619500	87.096891	50.515680	18.549609	813.091153
min	103.174973	60.060001	84.000000	121.080002	131.438278	72.843140	119.756897	40.592751	279.303253	92.651718	...	174.869995	56.027664	10.579879	112.904655	110.428238	95.384003	249.559998	173.635727	38.834499	3269.959961
25%	138.524902	85.519997	133.089996	171.820007	201.018570	103.111603	144.014450	50.373863	346.991150	252.285919	...	394.519989	88.638336	16.206352	134.108490	127.865417	201.880005	386.012970	206.614471	44.324261	4076.600098
50%	167.575714	102.900002	160.309998	194.190002	236.031769	131.928772	151.222504	56.363876	364.622620	316.861664	...	517.570007	105.146385	27.729065	153.950912	140.274200	240.080002	472.730499	225.511032	47.488297	4395.259766
75%	191.829453	137.179993	176.759995	212.009995	267.514801	154.275345	155.431381	59.936260	447.335083	473.209625	...	641.619995	125.442932	90.315811	161.462906	155.858002	282.160004	498.170715	269.519684	59.013657	5254.350098
max	249.534180	192.529999	237.679993	260.660004	340.623810	203.538910	164.740005	72.037811	584.808716	773.440002	...	1339.130005	160.342422	177.869995	177.486206	175.867111	404.600006	601.015259	363.944122	98.252411	6339.390137

8 rows × 21 columns

datos.info()

<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 61 entries, 2020-07-01 to 2025-07-01
Data columns (total 21 columns):
 #   Column  Non-Null Count  Dtype
---  ------  --------------  -----
 0   AAPL    61 non-null     float64
 1   AMD     61 non-null     float64
 2   AMZN    61 non-null     float64
 3   BA      61 non-null     float64
 4   CRM     61 non-null     float64
 5   GOOGL   61 non-null     float64
 6   JNJ     61 non-null     float64
 7   KO      61 non-null     float64
 8   MA      61 non-null     float64
 9   META    61 non-null     float64
 10  MSFT    61 non-null     float64
 11  NFLX    61 non-null     float64
 12  NKE     61 non-null     float64
 13  NVDA    61 non-null     float64
 14  PEP     61 non-null     float64
 15  PG      61 non-null     float64
 16  TSLA    61 non-null     float64
 17  UNH     61 non-null     float64
 18  V       61 non-null     float64
 19  WMT     61 non-null     float64
 20  ^GSPC   61 non-null     float64
dtypes: float64(21)
memory usage: 10.5 KB

Variables:

Se usaran indicadores financieros para agrupar a las acciones:

• Rendimiento medio mensual.

• Volatilidad mensual.

• Asimetría (Skewness).

• Curtosis.

• Coeficiente Beta: mide la sensibilidad del rendimiento de una acción frente a los movimientos del mercado, indicando cuánto tiende a variar la acción en relación con el índice de referencia.

def calcular_indicadores(serie_accion, serie_indice):
    retornos = serie_accion.pct_change().dropna()
    beta = np.cov(retornos, serie_indice.pct_change().dropna())[0, 1] / np.var(serie_indice.pct_change().dropna())
    return {
        'Retorno': retornos.mean(),
        'Volatilidad': retornos.std(),
        'Skewness': retornos.skew(),
        'Kurtosis': retornos.kurt(),
        'Beta': beta
    }

caracteristicas = []
for accion in acciones:
    caracteristicas.append(calcular_indicadores(datos[accion], datos[indice]))

df_indicadores = pd.DataFrame(caracteristicas, index=acciones)

df_indicadores.describe()

	Retorno	Volatilidad	Skewness	Kurtosis	Beta
count	20.000000	20.000000	20.000000	20.000000	20.000000
mean	0.016279	0.092425	0.051634	0.542927	1.153155
std	0.013544	0.041562	0.562000	1.361422	0.589540
min	0.001234	0.045147	-1.143828	-0.827875	0.392903
25%	0.008797	0.062848	-0.288277	-0.358962	0.615435
50%	0.012891	0.079984	0.123930	-0.230196	1.125789
75%	0.020063	0.119030	0.306699	1.171872	1.420758
max	0.058650	0.203409	1.035206	4.428854	2.369970

Matriz de correlación:

# Matriz de correlación entre las variables:
import seaborn as sns

plt.figure(figsize=(8, 6))
sns.heatmap(df_indicadores.corr(), annot=True, cmap='coolwarm', fmt=".2f", linewidths=.5)
plt.title('Mapa de Calor de Correlaciones de Indicadores')
plt.show()

PCA:

# Escalado de datos:
from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_scaled = scaler.fit_transform(df_indicadores)

from sklearn.decomposition import PCA

# Aplicación de PCA estándar
pca = PCA()
pca.fit(X_scaled)

# Cálculo de las varianzas explicadas
explained_variance = pca.explained_variance_ratio_

print("Varianza explicada por cada componente principal:")
print(explained_variance)

# Cálculo de la varianza explicada acumulada
explained_variance_cum = np.cumsum(pca.explained_variance_ratio_)

# Visualización del gráfico de varianza explicada
plt.figure(figsize=(8, 6))
plt.plot(
    range(1, len(explained_variance_cum) + 1),
    explained_variance_cum,
    marker="o",
    linestyle="--",
)
plt.xlabel("Número de Componentes Principales")
plt.ylabel("Varianza Explicada Acumulada")
plt.title("Gráfico de Varianza Explicada Acumulada")
plt.grid()
plt.show()

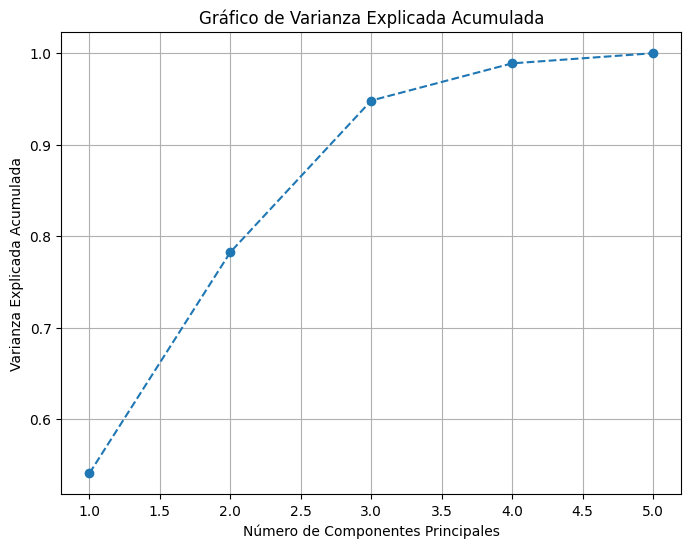
Varianza explicada por cada componente principal:
[0.54110558 0.24154776 0.16562478 0.04064715 0.01107473]

Cargas:

El análisis de cargas factoriales muestra que la Componente 1 está fuertemente asociada con retorno, volatilidad y beta, lo que sugiere que esta dimensión captura principalmente la dinámica conjunta entre rendimiento y riesgo sistemático de los activos.

Por su parte, la Componente 2 presenta una elevada correlación con asimetría y curtosis, aunque en el caso de la curtosis la relación es de signo inverso. Esto indica que esta componente refleja patrones de distribución no normales en los retornos (asimetrías y concentraciones de probabilidad en las colas).

En conjunto, las dos primeras componentes explican aproximadamente el 78% de la varianza total de los datos, lo cual evidencia una representación adecuada de la estructura de las variables originales. De esta manera, las cinco variables se encuentran bien representadas en las dos primeras dimensiones.

Cabe resaltar que en la Componente 3, tanto la asimetría como la curtosis exhiben una correlación positiva de magnitud moderada, lo que sugiere la existencia de un factor adicional que captura ciertos rasgos residuales de la forma de la distribución.

loadings = pca.components_.T * np.sqrt(pca.explained_variance_)
loadings_df = pd.DataFrame(
    loadings,
    columns=[f"PC{i+1}" for i in range(df_indicadores.shape[1])],
    index=df_indicadores.columns,
)
loadings_df

	PC1	PC2	PC3	PC4	PC5
Retorno	0.856260	0.063447	-0.457865	0.324702	-0.018812
Volatilidad	0.987746	-0.052716	0.090212	-0.197655	-0.164328
Skewness	0.212222	0.805643	0.584004	0.131967	-0.007552
Kurtosis	0.324036	-0.780401	0.559344	0.159228	0.019692
Beta	0.994516	0.080084	-0.002253	-0.163293	0.174601

Componentes: 2

# Aplicación de PCA estándar
num_components = 2
pca = PCA(n_components=num_components)
X_pca = pca.fit_transform(X_scaled)

# Varianza explicada:
explained_variance_ratio = pca.explained_variance_ratio_
cumulative_variance = np.cumsum(explained_variance_ratio)
cumulative_variance

array([0.54110558, 0.78265334])

Matríz de rotación:

rotation_matrix = pd.DataFrame(
    pca.components_.T,
    columns=[f"PC{i+1}" for i in range(num_components)],
    index=df_indicadores.columns,
)

print(rotation_matrix)

                  PC1       PC2
Retorno      0.507389  0.056272
Volatilidad  0.585304 -0.046753
Skewness     0.125755  0.714526
Kurtosis     0.192012 -0.692138
Beta         0.589315  0.071027

Cargas de las variables:

loadings = pca.components_.T * np.sqrt(pca.explained_variance_)
loadings_df = pd.DataFrame(
    loadings,
    columns=[f"PC{i+1}" for i in range(num_components)],
    index=df_indicadores.columns,
)
loadings_df

	PC1	PC2
Retorno	0.856260	0.063447
Volatilidad	0.987746	-0.052716
Skewness	0.212222	0.805643
Kurtosis	0.324036	-0.780401
Beta	0.994516	0.080084

Cálculo de la matriz de proyección:

projected_data = X_scaled @ pca.components_.T
projected_df = pd.DataFrame(
    projected_data,
    columns=[f"PC{i+1}" for i in range(num_components)],
    index=df_indicadores.index,
)
projected_df

	PC1	PC2
JNJ	-2.009927	0.571023
PG	-1.862686	0.698475
KO	-1.628735	-0.195235
PEP	-1.904777	0.749386
WMT	-1.077136	-0.514352
AAPL	-0.340766	0.870143
MSFT	-0.463062	0.726591
V	-0.846577	0.742175
MA	-0.636976	0.384738
UNH	-1.443072	-2.101111
TSLA	4.017179	0.810890
NVDA	3.314539	0.545678
META	0.854471	-1.035090
AMZN	-0.003152	0.022272
NFLX	1.473487	-3.536336
GOOGL	-0.469659	-0.278302
AMD	1.848918	1.107993
CRM	0.695677	0.488226
BA	1.065754	-0.027128
NKE	-0.583498	-0.030033

X_pca

array([[-2.00992661e+00,  5.71023056e-01],
       [-1.86268621e+00,  6.98474566e-01],
       [-1.62873530e+00, -1.95235456e-01],
       [-1.90477735e+00,  7.49385720e-01],
       [-1.07713606e+00, -5.14352008e-01],
       [-3.40766071e-01,  8.70143063e-01],
       [-4.63062470e-01,  7.26590620e-01],
       [-8.46576773e-01,  7.42174674e-01],
       [-6.36975870e-01,  3.84738442e-01],
       [-1.44307229e+00, -2.10111131e+00],
       [ 4.01717943e+00,  8.10889523e-01],
       [ 3.31453916e+00,  5.45678433e-01],
       [ 8.54470784e-01, -1.03509043e+00],
       [-3.15242929e-03,  2.22716935e-02],
       [ 1.47348699e+00, -3.53633606e+00],
       [-4.69659069e-01, -2.78301948e-01],
       [ 1.84891788e+00,  1.10799255e+00],
       [ 6.95676720e-01,  4.88225688e-01],
       [ 1.06575383e+00, -2.71275852e-02],
       [-5.83498308e-01, -3.00332323e-02]])

plt.figure(figsize=(10, 6))

# Gráfico de las observaciones (acciones)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c='blue')

# Etiquetas de las observaciones (acciones)
for i, label in enumerate(df_indicadores.index):
    plt.annotate(label, (X_pca[i, 0], X_pca[i, 1]),
                 fontsize=8, alpha=0.7)

# Añadir las cargas (loadings) como flechas rojas
for i, var in enumerate(df_indicadores.columns):
    plt.arrow(0, 0, loadings[i, 0], loadings[i, 1],
              color='crimson', alpha=0.8,
              head_width=0.05, length_includes_head=True)
    plt.text(loadings[i, 0]*1.4, loadings[i, 1]*1.1, var,
             color='crimson', ha='center', va='center', fontsize=9)

# Configuración del gráfico
plt.title('PCA de Indicadores Financieros (Biplot)')
plt.xlabel(f'Componente Principal 1 ({explained_variance_ratio[0]*100:.1f}%)')
plt.ylabel(f'Componente Principal 2 ({explained_variance_ratio[1]*100:.1f}%)')
plt.axhline(0, color='gray', lw=1)
plt.axvline(0, color='gray', lw=1)
plt.grid(True)
plt.tight_layout()
plt.show()

Dato nuevo:

# Nueva acción:
new_data = yf.download(["DIS"], start='2020-07-01', end='2025-07-31', interval='1mo')['Close']
new_data.dropna(inplace=True)

/tmp/ipython-input-1044502549.py:2: FutureWarning: YF.download() has changed argument auto_adjust default to True
  new_data = yf.download(["DIS"], start='2020-07-01', end='2025-07-31', interval='1mo')['Close']
[*******************100%*********************]  1 of 1 completed

# Calcular indicadores con la misma función:
indicadores_new = calcular_indicadores(new_data["DIS"], datos[indice])

# Convertir a DataFrame para que tenga el mismo formato:
df_new = pd.DataFrame([indicadores_new], index=["DIS"])
df_new

	Retorno	Volatilidad	Skewness	Kurtosis	Beta
DIS	0.00573	0.104237	0.635961	-0.016636	1.59273

# Escalar con el scaler ya entrenado en tus datos originales:
X_new_scaled = scaler.transform(df_new)

# Proyectar en el espacio PCA ya entrenado:
X_new_pca = pca.transform(X_new_scaled)

print(f"Coordenadas de {"DIS"} en PC1 y PC2:", X_new_pca)

Coordenadas de DIS en PC1 y PC2: [[0.2691755  1.04981175]]

plt.figure(figsize=(10, 6))
plt.scatter(X_pca[:, 0], X_pca[:, 1], c='blue', label='Acciones originales')

for i, label in enumerate(df_indicadores.index):
    plt.annotate(label, (X_pca[i, 0], X_pca[i, 1]), fontsize=8, alpha=0.7)

# Nueva acción
plt.scatter(X_new_pca[0, 0], X_new_pca[0, 1], c='darkgreen', marker='X', s=110, label=df_new.index[0])
plt.annotate(df_new.index[0], (X_new_pca[0, 0], X_new_pca[0, 1]), fontsize=9, color='red')

# Flechas de cargas (asumiendo 'loadings' ya calculado)
for i, var in enumerate(df_indicadores.columns):
    plt.arrow(0, 0, loadings[i, 0], loadings[i, 1],
              color='crimson', alpha=0.8, head_width=0.05, length_includes_head=True)
    plt.text(loadings[i, 0]*1.4, loadings[i, 1]*1.1, var,
             color='crimson', ha='center', va='center', fontsize=9)

plt.title('PCA de Indicadores Financieros (con nueva acción)')
plt.xlabel(f'PC1 ({explained_variance_ratio[0]*100:.1f}%)')
plt.ylabel(f'PC2 ({explained_variance_ratio[1]*100:.1f}%)')
plt.axhline(0, color='gray', lw=1); plt.axvline(0, color='gray', lw=1)
plt.legend(); plt.grid(True); plt.tight_layout(); plt.show()

Advertencia:

Al aplicar PCA con menos componentes que las variables originales, el inverse_transform no recupera los datos originales, sino una aproximación que conserva solo la varianza capturada por esas componentes.

K-Means:

from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans, DBSCAN
from sklearn.metrics import silhouette_score, pairwise_distances_argmin_min
from scipy.cluster.hierarchy import dendrogram, linkage, fcluster

# Calcular WCSS para diferentes valores de K:
wcss = []
K = range(1, 10)
for k in K:
    kmeans = KMeans(n_clusters=k, random_state=34)
    kmeans.fit(X_pca)
    wcss.append(kmeans.inertia_)

# Visualizar el método del codo
plt.figure(figsize=(8, 4))
plt.plot(K, wcss, "bo-")
plt.xlabel("Número de clústeres (K)")
plt.ylabel("WCSS")
plt.title("Método del Codo para determinar el número óptimo de clústeres")
plt.show()

# Calcular la puntuación de la silueta para diferentes valores de K:
from sklearn.metrics import silhouette_score

silhouette_scores = []
K = range(2, 11)
for k in K:
    kmeans = KMeans(n_clusters=k, random_state=34)
    kmeans.fit(X_pca)
    labels = kmeans.labels_
    score = silhouette_score(X_scaled, labels)
    silhouette_scores.append(score)

# Visualizar la puntuación de la silueta
plt.figure(figsize=(8, 4))
plt.plot(K, silhouette_scores, "bo-")
plt.xlabel("Número de clústeres (K)")
plt.ylabel("Puntuación de la Silueta")
plt.title("Método de la Silueta para determinar el número óptimo de clústeres")
plt.show()

Clusters = 3

k_base = 3

kmeans = KMeans(n_clusters=k_base, random_state=34)
df_indicadores_copy = df_indicadores.copy()
df_indicadores_copy['Cluster_KMeans'] = kmeans.fit_predict(X_pca)

# Valores de Inercia y Silueta:
inercia = kmeans.inertia_
silhouette = silhouette_score(X_pca, df_indicadores_copy['Cluster_KMeans'])

print(f"Clusters: {k_base}")
print(f"Inercia: {inercia}")
print(f"Puntuación de la Silueta: {silhouette}")

Clusters: 3
Inercia: 25.062446862137296
Puntuación de la Silueta: 0.4597279703983844

def graficar_clusters(df, metodo, var_x='Volatilidad', var_y='Retorno'):
    plt.figure(figsize=(10, 6))
    sns.scatterplot(
        data=df,
        x=var_x,
        y=var_y,
        hue=f'Cluster_{metodo}',
        palette='Set1',
        s=120
    )
    for i in range(len(df)):
        plt.text(df[var_x].iloc[i] + 0.002, df[var_y].iloc[i], df.index[i], fontsize=9)

    plt.title(f'Clustering por {metodo}: {var_y} vs {var_x}')
    plt.xlabel(var_x)
    plt.ylabel(var_y)
    plt.legend(title='Cluster')
    plt.grid(True)
    plt.show()

# Graficar cada método
graficar_clusters(df_indicadores_copy, 'KMeans')

# Clustering y variables en escala estandarizada:
labels = kmeans.labels_
X_scaled_df = pd.DataFrame(X_scaled, columns=df_indicadores_copy.iloc[:,:-1].columns)
X_scaled_df['Cluster_KMeans'] = labels

import plotly.graph_objects as go

# Columnas a usar
cols = ['Retorno','Volatilidad','Skewness','Kurtosis','Beta']

# Preparar datos y calcular promedio por cluster
tmp = X_scaled_df.copy()
tmp[cols] = tmp[cols].apply(pd.to_numeric, errors='coerce')
agg = tmp.groupby('Cluster_KMeans')[cols].mean().sort_index()

# Construir radar combinado
cats = cols + [cols[0]]
fig = go.Figure()

for cl, row in agg.iterrows():
    vals = row.tolist()
    fig.add_trace(go.Scatterpolar(
        r=vals + [vals[0]],
        theta=cats,
        name=f'Cluster {cl}',
        fill='toself',
        opacity=0.30
    ))

fig.update_layout(
    title='Radar combinado por cluster',
    template='plotly_white',
    polar=dict(radialaxis=dict(showline=False, gridcolor='lightgray'))
)

fig.show()