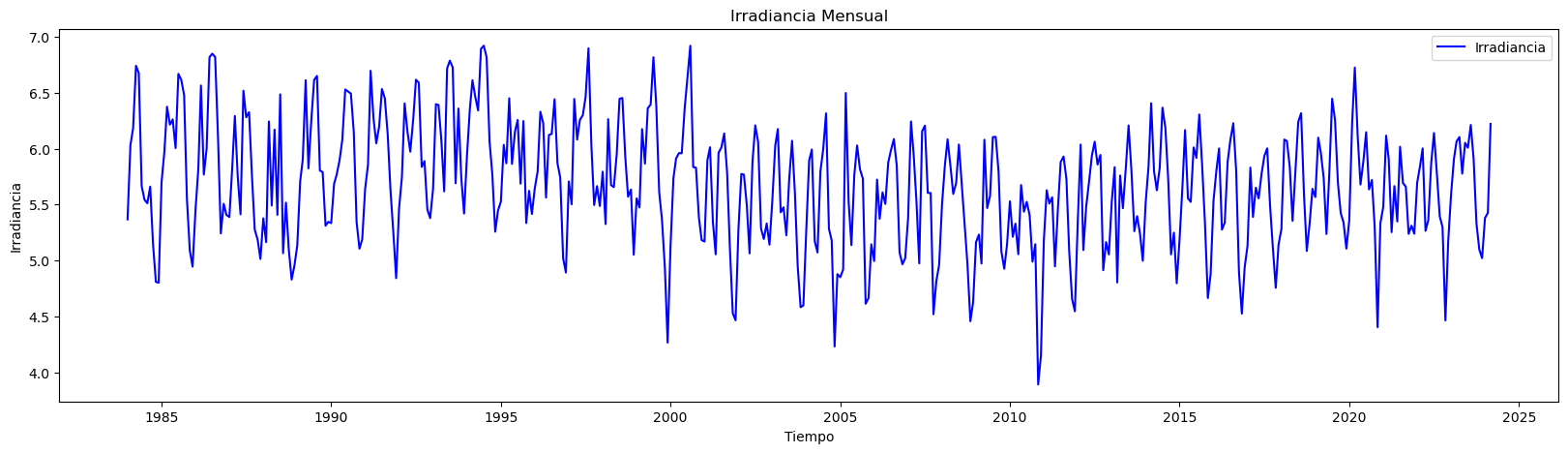
SVR para series de tiempo#
import numpy as np
import pandas as pd
from sklearn.svm import SVR
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
import matplotlib.pyplot as plt
import scipy.stats as stats
import seaborn as sns
import warnings
# Suprimir todas las advertencias
warnings.filterwarnings("ignore")
# Cargar los datos omitiendo la primera fila como encabezado y asignando nombres a las columnas
data = pd.read_csv("../Irradiance_mensual.csv", skiprows=1, header=None, names=["Fecha", "Irradiancia"])
# Convertir la columna 'Fecha' a datetime
data["Fecha"] = pd.to_datetime(data["Fecha"], format="%Y-%m")
# Set 'Fecha' as the index
data.set_index("Fecha", inplace=True)
# Cantidad de datos
n = data.shape[0]
print("Cantidad de datos:", n)
plt.figure(figsize=(20, 5)) # Establecer el tamaño del gráfico
plt.plot(
data.index, data["Irradiancia"], label="Irradiancia", color="blue"
) # Dibujar los datos reales
plt.title("Irradiancia Mensual") # Título del gráfico
plt.xlabel("Tiempo") # Etiqueta del eje X
plt.ylabel("Irradiancia") # Etiqueta del eje Y
plt.legend() # Añadir leyenda para identificar las líneas
plt.show()
Cantidad de datos: 483
Conjunto de Train y Test y escalado de datos:#
Las características (X) y la variable objetivo (y) deben
escalarse por separado utilizando StandardScaler o cualquier otro
método de escalado. Esto se debe a que las características y la variable
objetivo pueden tener diferentes unidades y rangos de valores.
Es crucial que los parámetros de escalado (media y desviación estándar)
sean calculados solo en los datos de entrenamiento (X_train y
y_train) para evitar fugas de información. El conjunto de prueba
(X_test y y_test) debe ser transformado usando los mismos
parámetros obtenidos del conjunto de entrenamiento.
# Definir características (X) y objetivo (y)
X = data[["Irradiancia"]] # Usar la irradiancia como característica
y = data["Irradiancia"] # Usar la irradiancia también como objetivo
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=False)
Usar shuffle=False al dividir los datos es crucial cuando se trabaja
con series de tiempo porque mantiene el orden temporal de los datos.
Con shuffle=True los datos, pierdes esta secuencia temporal, lo que
significa que podrías tener valores en el conjunto de prueba que
cronológicamente preceden a valores en el conjunto de entrenamiento, lo
que no tiene sentido para un modelo predictivo.
# Graficar X_train y X_test
plt.figure(figsize=(14, 7))
# Graficar X_train
plt.plot(X_train.index, X_train.values, label="X_train", color="blue")
# Graficar X_test
plt.plot(X_test.index, X_test.values, label="X_test", color="green")
plt.title("Conjunto de entrenamiento y prueba")
plt.xlabel("Fecha")
plt.ylabel("Irradiancia")
plt.legend()
plt.show()
# Crear una figura y ejes
fig, (ax_box, ax_hist) = plt.subplots(2, figsize=(10, 6), gridspec_kw={"height_ratios": (0.15, 0.85)})
# Gráfico de caja en la parte superior
sns.boxplot(data=[X_train, X_test], ax=ax_box, orient="h", palette="Set2")
ax_box.set(yticklabels=["Train", "Test"], xlabel=None)
ax_box.tick_params(left=False)
# Histograma de densidad en la parte inferior
sns.histplot(X_train, ax=ax_hist, kde=True, palette="Set2", label="Train", alpha=0.6)
sns.histplot(X_test, ax=ax_hist, kde=True, palette="Set1", label="Test", alpha=0.6)
# Mostrar la leyenda y el gráfico
ax_hist.legend()
plt.show()
# Crear escaladores para X e y
scaler_X = StandardScaler()
scaler_y = StandardScaler()
# Ajustar y transformar X_train, luego transformar X_test con el mismo escalador
X_train_scaled = scaler_X.fit_transform(X_train)
X_test_scaled = scaler_X.transform(X_test)
# Ajustar y transformar y_train, luego transformar y_test con el mismo escalador
y_train_scaled = scaler_y.fit_transform(y_train.values.reshape(-1, 1)).flatten()
y_test_scaled = scaler_y.transform(y_test.values.reshape(-1, 1)).flatten()
El uso de .flatten() en el contexto del código tiene como objetivo
convertir una matriz 2D en un arreglo 1D.
Cuando se utiliza StandardScaler para escalar los datos, el método
fit_transform() devuelve una matriz 2D, incluso si los datos
originales consisten en una sola columna. Por ejemplo, si y_train es
un vector con forma (n_samples,), después de aplicar
scaler_y.fit_transform(y_train.reshape(-1, 1)), se obtiene una
matriz con forma (n_samples, 1). Sin embargo, algunos modelos o
funciones en Python, como el SVR de scikit-learn, esperan que los datos
de salida (objetivo) estén en un formato de arreglo 1D, es decir, con
forma (n_samples,).
SVR:#
# Crear el modelo SVR
svr = SVR(kernel="rbf", C=1e3, epsilon=0.1)
# Entrenar el modelo con los datos de entrenamiento escalados
svr.fit(X_train_scaled, y_train_scaled)
SVR(C=1000.0)
Evaluación del modelo:#
Sobre conjunto de entrenamiento:
Se usa .inverse_transform para volver a las unidades originales
(desescalar).
# Predicciones en el conjunto de entrenamiento
y_pred_scaled_train = svr.predict(X_train_scaled)
# Transformar las predicciones a la escala original: desescalar
y_pred_train = scaler_y.inverse_transform(y_pred_scaled_train.reshape(-1, 1)).flatten()
# Calcular MAE
mae_train = mean_absolute_error(y_train, y_pred_train)
# Calcular MSE
mse_train = mean_squared_error(y_train, y_pred_train)
# Calcular RMSE
rmse_train = np.sqrt(mean_squared_error(y_train, y_pred_train))
# Calcular R^2
r2_train = r2_score(y_train, y_pred_train)
# Mostar métricas
print("Métricas en el conjunto de entrenamiento:")
print("Mean Absolute Error (MAE):", mae_train)
print("Mean Squared Error (MSE):", mse_train)
print("Root Mean Squared Error (RMSE):", rmse_train)
print("R² Score:", r2_train)
Métricas en el conjunto de entrenamiento:
Mean Absolute Error (MAE): 0.03976956453866239
Mean Squared Error (MSE): 0.0018272615089242122
Root Mean Squared Error (RMSE): 0.04274647949158167
R² Score: 0.9941573087931465
Sobre conjunto de prueba:
# Predicciones en el conjunto de prueba
y_pred_scaled = svr.predict(X_test_scaled)
# Transformar las predicciones a la escala original: desescalar
y_pred = scaler_y.inverse_transform(y_pred_scaled.reshape(-1, 1))
# Calcular MAE
mae = mean_absolute_error(y_test, y_pred)
# Calcular MSE
mse = mean_squared_error(y_test, y_pred)
# Calcular RMSE
rmse = np.sqrt(mse)
# Calcular R² Score
r2 = r2_score(y_test, y_pred)
# Mostrar las métricas
print("Métricas en el conjunto de entrenamiento:")
print(f"Mean Absolute Error (MAE): {mae}")
print(f"Mean Squared Error (MSE): {mse}")
print(f"Root Mean Squared Error (RMSE): {rmse}")
print(f"R² Score: {r2}")
Métricas en el conjunto de entrenamiento:
Mean Absolute Error (MAE): 0.03907725352485998
Mean Squared Error (MSE): 0.001825688634054782
Root Mean Squared Error (RMSE): 0.04272807781839457
R² Score: 0.9906490284012837
# Gráfica de resultados
plt.figure(figsize=(14, 7))
plt.plot(y_test.index, y_test.values, label="Test", color="green")
plt.plot(y_test.index, y_pred, label="Predicted", linestyle="--", color="red")
plt.title("Ajuste modelo SVR")
plt.xlabel("Fecha")
plt.ylabel("Irradiancia")
plt.legend()
plt.show()
Análisis de los residuales:#
# Calcular los residuales sobre train
y_pred_train_scaled = svr.predict(X_train_scaled)
y_pred_train = scaler_y.inverse_transform(y_pred_train_scaled.reshape(-1, 1))
residuals_train = y_train.values - y_pred_train.flatten()
# Configuración de la figura para los subplots
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(14, 6))
# Gráfico de valores predichos vs. valores reales
axs[0].scatter(y_pred_train.flatten(), y_train.values, color="blue", alpha=0.5)
axs[0].plot(
[y_train.min(), y_train.max()], [y_train.min(), y_train.max()], "k--", lw=2
) # Línea diagonal ideal
axs[0].set_title("Valores Reales vs. Valores Predichos")
axs[0].set_xlabel("Valores Predichos")
axs[0].set_ylabel("Valores Reales")
# Gráfico de residuales
axs[1].scatter(y_train.index, residuals_train, color="purple", alpha=0.3)
axs[1].axhline(y=0, color="black", linestyle="--") # Línea en y=0 para referencia
axs[1].set_title("Gráfico de Residuales")
axs[1].set_xlabel("Fecha")
axs[1].set_ylabel("Residuales")
# Mejorar el layout para evitar solapamientos
plt.tight_layout()
# Mostrar la figura
plt.show()
# Visualización del histograma de los residuos
plt.figure(figsize=(14, 6))
plt.subplot(1, 2, 1)
plt.hist(residuals_train, bins=20, color="skyblue", edgecolor="black")
plt.title("Histograma de Residuos")
plt.xlabel("Residuos")
plt.ylabel("Frecuencia")
# Visualización del gráfico Q-Q de los residuos
plt.subplot(1, 2, 2)
stats.probplot(residuals_train, dist="norm", plot=plt)
plt.title("Gráfico Q-Q de Residuos")
# Ajustar el diseño de la figura
plt.tight_layout()
# Mostrar la figura
plt.show()
Predicciones fuera de la muestra:#
# Último valor de X_test_scaled
last_X = X_test_scaled[-1].reshape(1, -1)
last_X
array([[0.94242876]])
# Número de pasos adelante para predecir
n_steps_ahead = 12 * 5
# Array para almacenar las predicciones fuera de muestra
predictions_out_of_sample = []
for _ in range(n_steps_ahead):
# Hacer la predicción usando el último valor de X
pred_scaled = svr.predict(last_X)
# Desescalar la predicción para obtener el valor original
pred = scaler_y.inverse_transform(pred_scaled.reshape(-1, 1)).flatten()[0]
# Guardar la predicción desescalada
predictions_out_of_sample.append(pred)
# Crear la nueva entrada para la siguiente predicción
last_X = scaler_X.transform(np.array([[pred]])) # Escalar la nueva entrada
# Convertir las predicciones fuera de muestra en un array de numpy
predictions_out_of_sample = np.array(predictions_out_of_sample)
# Asegúrate de que los índices de tiempo estén en formato de fechas
dates_out_of_sample = pd.date_range(
start=y_test.index[-1], periods=n_steps_ahead + 1, freq="M"
)[1:]
# Gráfico de las predicciones fuera de muestra
plt.figure(figsize=(10, 6))
plt.plot(y_train.index, y_train, label="Train")
plt.plot(y_test.index, y_test, label="Test")
plt.plot(
dates_out_of_sample,
predictions_out_of_sample,
label="Predicciones fuera de la muestra",
color="red",
linestyle="--",
)
plt.title("Predicciones fuera de la muestra con SVR")
plt.xlabel("Fecha")
plt.ylabel("Irradiancia")
plt.legend()
plt.show()