CNN para series de tiempo#
Las mismas propiedades que hacen que las CNN sobresalgan en el área de visión también las hacen muy relevantes para el procesamiento de secuencias debido a que el tiempo se puede tratar como una dimensión espacial, como la altura o el ancho de una imagen en 2D. Además, las pequeñas redes 1D pueden ofrecer una alternativa rápida a las RNN para tareas simples como la clasificación de texto y en el pronóstico de series temporales.
Capa convolucional 1D para datos secuenciales:#
En las CNN, se extraen fragmentos de la imagen en 2D y se le aplica una transformación idéntica a cada patch, de la misma forma, se puede usar una capa convolucional de 1 dimensión, extrayendo subsecuencias de una secuencia más grande.
1D-CNN#
En el ejemplo anterior se procesan secuencias con 1D-CNN utilizando ventanas de convolución de tamaño 5. Con esto se debería poder aprender palabras o fragmentos de palabras de 5 caracteres o de menor longitud y se debería poder reconocer estas palabras en cualquier contexto en una secuencia de entrada. Por lo tanto, una 1D-CNN a nivel de carácter puede aprender sobre la morfología de las palabras.
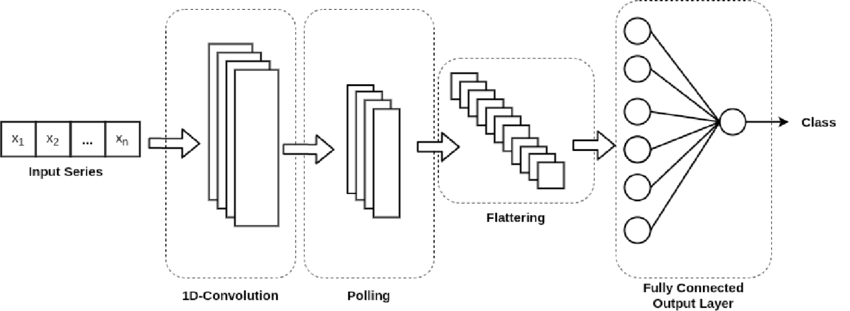
CNN-ts#
Con Keras se puede usar una CNN con la capa Conv1D la cual tiene una
interface similar a una capa Conv2D. Esta toma como entrada un
Tensor 3D con la forma (samples, time_step, features) y retorna un
tensor 3D de forma similar. La ventana de convolución es una ventana de
una dimensión sobre el eje temporal.
Capas de convolución Conv1D de Keras que usaremos para series de
tiempo
aquí
Se debe especificar la cantidad de kernels o filtros de esta capa con el
argumento filters= y el tamaño de cada filtro con el argumento
kernel_size=. Por defecto strides=1 y padding="valid".
"valid" significa que no hace padding, pero se puede especificar
"same" para que la salida tenga la misma dimensión que la entrada.
La función de activación se especifica con activation=.
Si se agrega en la primera capa oculta Conv1D, se debe especificar
input_shape=. Esto es lo que el modelo espera como entrada para cada
muestra (sample) en términos de la cantidad de pasos de tiempo (time
step) y la cantidad de características (features). Estamos trabajando
con una serie univariante, por lo que el número de features es uno, para
una variable. El número de pasos de tiempo como entrada es el número que
elegimos al preparar nuestro conjunto de datos como argumento para la
función split sequence(). La forma de entrada para cada muestra se
especifica en el argumento de forma de entrada en la definición de la
primera capa oculta. Casi siempre tenemos múltiples muestras, por lo
tanto, el modelo esperará que el componente de entrada de los datos de
entrenamiento tenga las dimensiones o la forma:
[samples, time_step, features].
La CNN en realidad no considera que los datos tengan pasos de tiempo, sino que los trata como una secuencia sobre la cual se pueden realizar operaciones de lectura convolucionales, como una imagen unidimensional.
Capa de MaxPooling 1D para datos secuenciales:#
La capa de Keras para para el agrupamiento máximo o Max-pooling para
datos secuenciales se llama MaxPooling1D
aquí
Por defecto pool_size=2.
El argumento strides= especifica cuánto se mueve la ventana de
agrupación para cada paso de agrupación. Por defecto es igual que
pool_size si no se especifica.
El argumento padding= tiene dos opciones: "valid" para no hacer
padding o "same" para que la salida tenga la misma dimensión que la
entrada.
Código:#
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import yfinance as yf
from sklearn.preprocessing import StandardScaler
import warnings # Para ignorar mensajes de advertencia
warnings.filterwarnings("ignore")
Descargar datos desde Yahoo Finance:#
tickers = ["ES=F"]
ohlc = yf.download(tickers, period="max")
print(ohlc.tail())
[*******************100%*********************] 1 of 1 completed
Open High Low Close Adj Close Volume
Date
2022-08-29 4024.00 4064.00 4006.75 4031.25 4031.25 1963446
2022-08-30 4035.75 4072.75 3964.50 3987.50 3987.50 2555455
2022-08-31 3987.25 4018.25 3953.00 3956.50 3956.50 2366488
2022-09-01 3958.00 3971.25 3903.50 3968.75 3968.75 2212034
2022-09-02 3967.50 4019.25 3906.00 3924.50 3924.50 2212034
df = ohlc["Adj Close"].dropna(how="all")
df.tail()
Date
2022-08-29 4031.25
2022-08-30 3987.50
2022-08-31 3956.50
2022-09-01 3968.75
2022-09-02 3924.50
Name: Adj Close, dtype: float64
df = np.array(df[:, np.newaxis])
df.shape
(5551, 1)
plt.figure(figsize=(10, 6))
plt.plot(df)
plt.show()
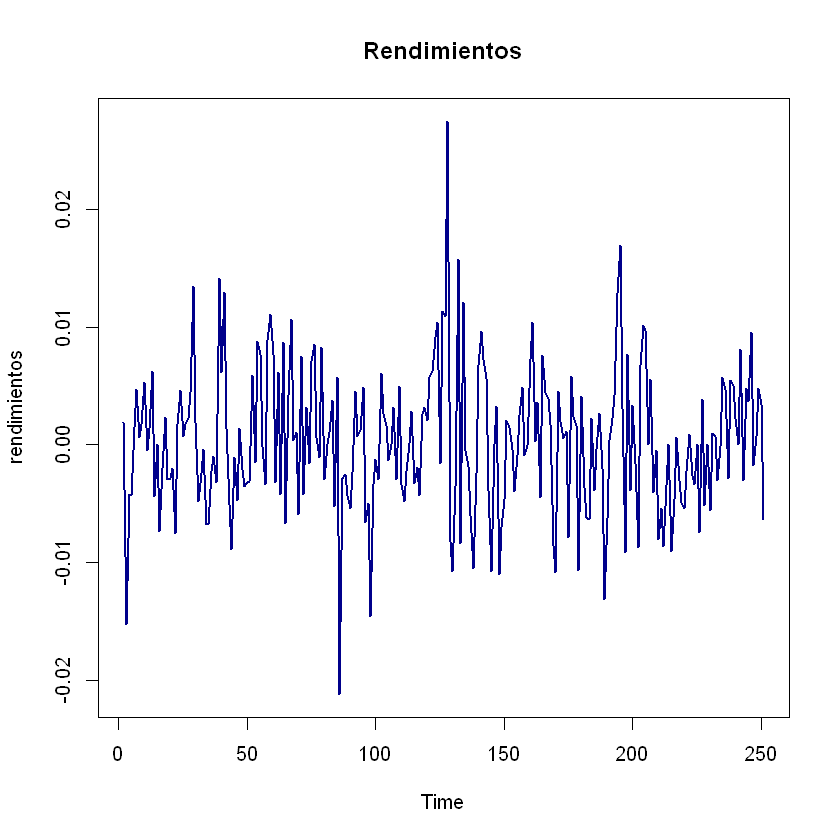
Conjunto de train y test:#
time_test = 0.10
train = df[: int(len(df) * (1 - time_test))]
test = df[int(len(df) * (1 - time_test)) :]
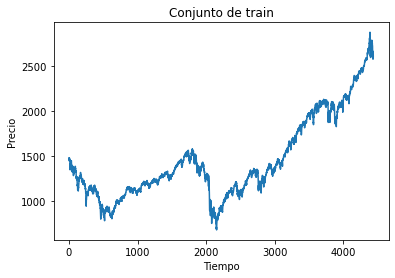
plt.plot(train)
plt.xlabel("Tiempo")
plt.ylabel("Precio")
plt.title("Conjunto de train")
plt.show()
plt.plot(test)
plt.xlabel("Tiempo")
plt.ylabel("Precio")
plt.title("Conjunto de test")
plt.show()
Función para conformar el dataset para datos secuenciales:
def split_sequence(sequence, time_step):
X, y = list(), list()
for i in range(len(sequence)):
end_ix = i + time_step
if end_ix > len(sequence) - 1:
break
seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
X.append(seq_x)
y.append(seq_y)
return np.array(X), np.array(y)
time_step = 10
X_train, y_train = split_sequence(train, time_step)
X_test, y_test = split_sequence(test, time_step)
X_train.shape
(4985, 10, 1)
X_test.shape
(546, 10, 1)
Arquitectura de la red con CNN:#
El siguiente ejemplo tendrá dos capas de convolución, pero solo se
aplica pooling a la salida de la segunda capa Conv1D. Se podría
agregar pooling a la salida de cada capa de convolución. Luego, se
agrega una capa Flatten para conectar la red neuronal artificial.
Esta RNA solo tiene una capa oculta, pero se podrían agregar varias
capas ocultas. Es común agregar capas Dropout en la RNA porque se
usan muchas neuronas y así evitar el overfitting.
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Conv1D
from keras.layers import MaxPooling1D
from keras.layers import Flatten
model = Sequential()
model.add(Conv1D(filters=64, kernel_size=2, activation='relu', input_shape=(time_step,1))) # Capa convolucional 1
model.add(Conv1D(filters=32, kernel_size=2, activation='relu')) # Capa convolucional 2
model.add(MaxPooling1D(pool_size=2)) # Max-Pooling
model.add(Flatten()) # Capa Flatten
model.add(Dense(50, activation='relu'))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')
history = model.fit(
X_train,
y_train,
validation_data=(X_test, y_test),
epochs=30,
batch_size=32,
verbose=0
)
Evaluación del desempeño:#
rmse = model.evaluate(X_test, y_test, verbose=0) ** 0.5
rmse
61.185935883992165
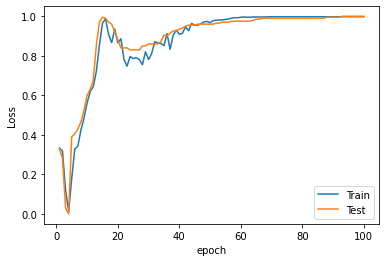
plt.plot(range(1, len(history.epoch) + 1), history.history["loss"], label="Train")
plt.plot(range(1, len(history.epoch) + 1), history.history["val_loss"], label="Test")
plt.xlabel("epoch")
plt.ylabel("Loss")
plt.legend();
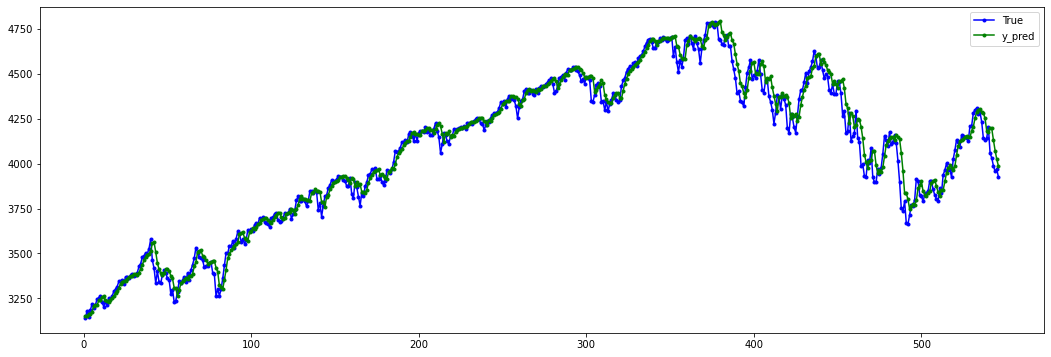
Predicción del modelo:#
y_pred = model.predict(X_test, verbose=0)
y_pred[0:5]
array([[3153.7463],
[3153.6313],
[3162.04 ],
[3164.2183],
[3173.7153]], dtype=float32)
plt.figure(figsize=(18, 6))
plt.plot(
range(1, len(X_test) + 1),
test[time_step:, :],
color="b",
marker=".",
linestyle="-",
label="True"
)
plt.plot(
range(1, len(X_test) + 1),
y_pred,
color="g",
marker=".",
linestyle="-",
label="y_pred"
)
plt.legend();
Predicción fuera de la muestra:#
predictions = []
time_prediction = 20 # cantidad de predicciones fuera de la muestra
first_sample = df[-time_step:, 0] # última muestra dentro de la serie de tiempo
current_batch = first_sample[np.newaxis] # Transformación en muestras y time step
current_batch = np.reshape(current_batch, (1, time_step, 1)) # Transformación en 3D
for i in range(time_prediction):
current_pred = model.predict(current_batch, verbose=0)[0]
# Guardar la predicción
predictions.append(current_pred)
# Actualizar el lote para incluir ahora la predicción y soltar el primer valor (primer time step)
current_batch = np.append(current_batch[:, 1:], [[current_pred]])[np.newaxis]
current_batch = np.reshape(current_batch, (1, time_step, 1)) # Transformación en 3D
plt.figure(figsize=(10, 6))
plt.plot(
range(1, len(df[-100:, 0]) + 1),
df[-100:, 0],
color="b",
marker=".",
linestyle="-",
label="True"
)
plt.plot(
range(len(df[-100:, 0]) + 1, len(df[-100:, 0]) + len(predictions) + 1),
predictions,
color="g",
marker=".",
linestyle="-",
label="y_pred fuera de la muestra"
)
plt.legend();