Autocorrelación Parcial-PACF#
La Función de Autocorrelación Parcial (PACF) mide la correlación directa entre los valores de una serie de tiempo separados por \(k\) periodos, eliminando el efecto de los rezagos intermedios.
Mientras que la ACF muestra la relación total (directa e indirecta) entre \(y_t\) y \(y_{t-k}\), la PACF muestra sólo la parte directa entre esos dos puntos.
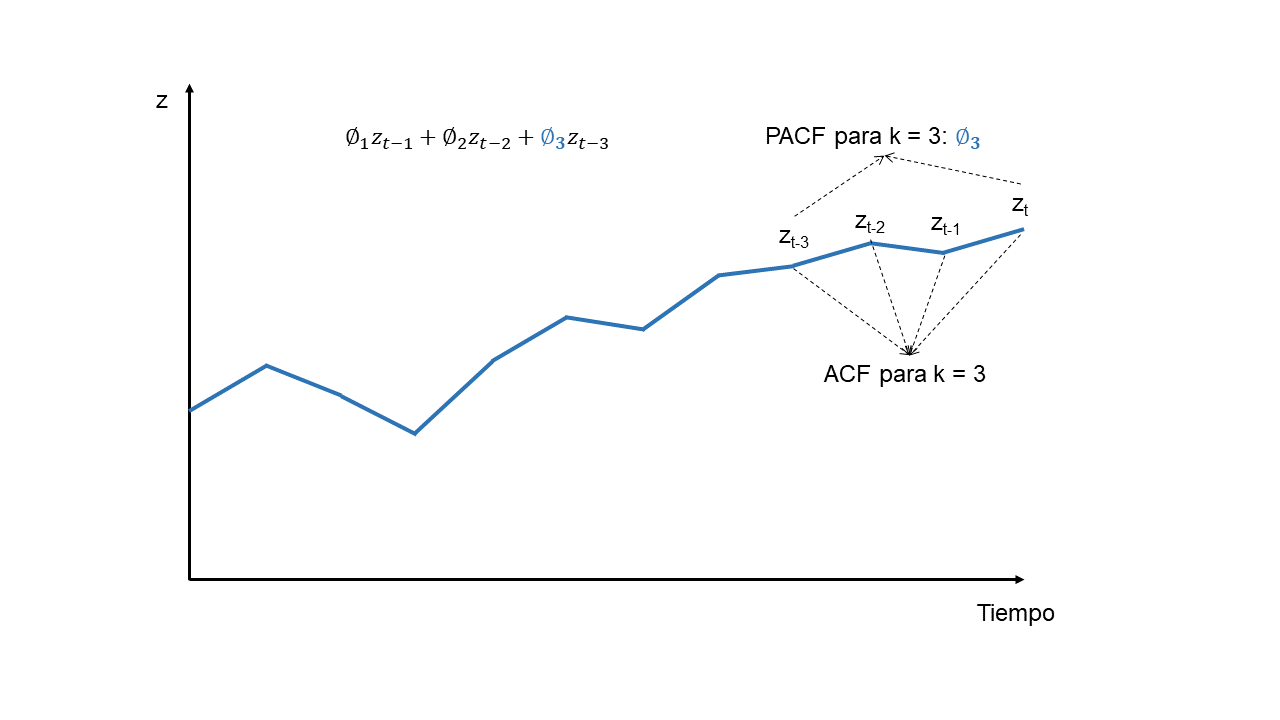
PACFvsACF#
Motivación: ¿Por qué necesitamos la PACF?
En procesos autorregresivos (AR), los valores pasados afectan al presente, pero también entre sí.
La ACF no distingue entre la influencia directa y la indirecta: por ejemplo, la correlación entre \(y_t\) y \(y_{t-2}\) incluye la influencia de \(y_{t-1}\) como “puente”.
La PACF elimina ese “efecto puente” y mide la correlación neta entre \(y_t\) y \(y_{t-k}\).
Definición formal:
El coeficiente de autocorrelación parcial en el lag \(k\) (\(\phi_{kk}\)) es la correlación entre \(y_t\) y \(y_{t-k}\) condicionada a los valores intermedios \(y_{t-1}, y_{t-2}, ..., z_{t-k+1}\).
Es el último coeficiente del modelo AR(\(k\)) estimado por regresión múltiple.
¿Cómo se interpreta la PACF?
En un proceso AR(p), la PACF es significativa solo hasta el rezago :math:`p` y para lags mayores cae rápidamente a cero.
Por eso, el número de rezagos significativos en la PACF indica el orden :math:`p` de un modelo AR(p).
La ACF es mejor para identificar el orden \(q\) de un MA(q), la PACF es clave para determinar el \(p\) de un AR(p).
Comparación ACF vs PACF
ACF |
PACF |
|
|---|---|---|
Mide |
Correlación total (directa + indirecta) |
Correlación directa |
Útil para |
Identificar orden MA(q) |
Identificar orden AR(p) |
Patrón AR |
Caída exponencial o lenta |
Corte brusco después de lag p |
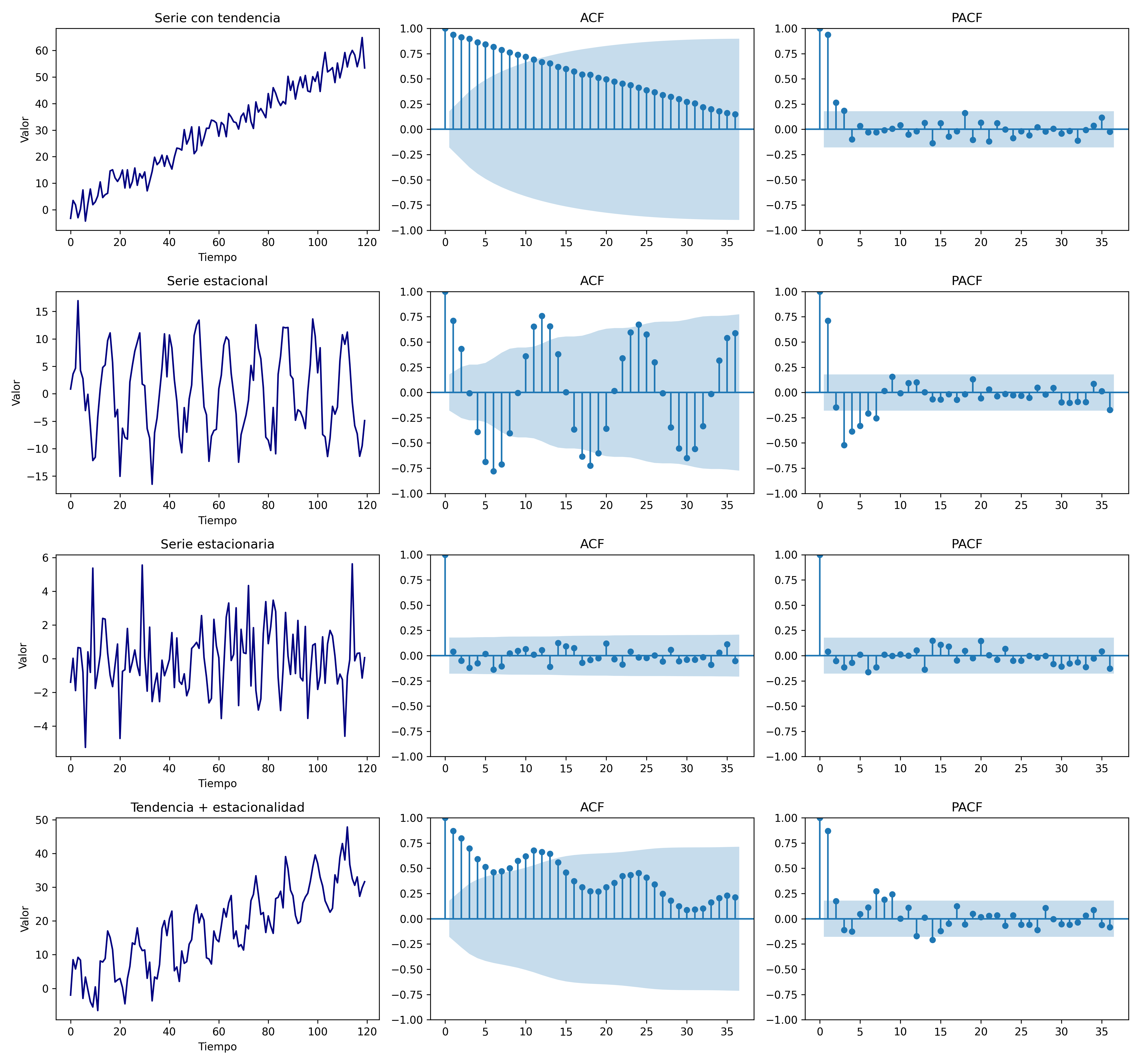
acf_pacf_series#
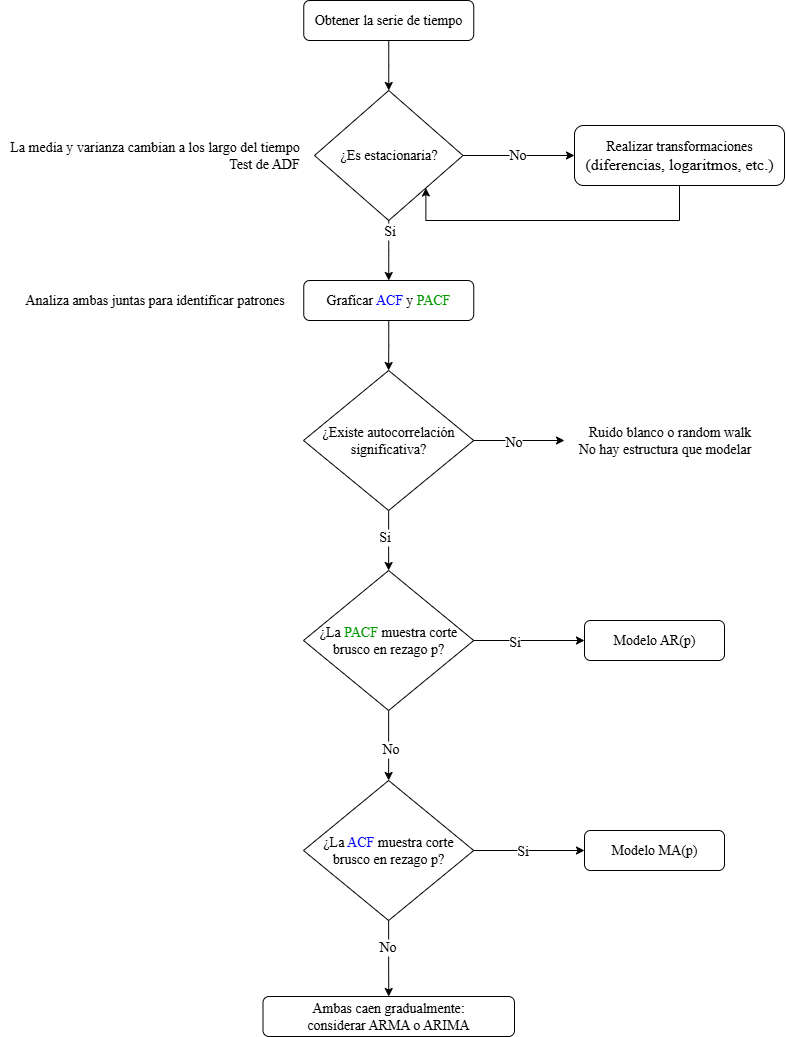
Diagrama_ACF_PACF#
** Serie / Mod elo** |
ACF |
PACF |
Mo delo Su geri do |
Patrón visual clave |
|---|---|---|---|---|
Ruido b lanco |
Todos los rezagos dentro de la franja, no significativos |
Todos los rezagos dentro de la franja, no si gnificativos |
Nin guno / P aseo a leat orio |
No hay correlaciones, ni en ACF ni en PACF |
AR(p) |
Decae gradualmente (exponencial u oscilante) |
Corte brusco en lag p (s ignificativo hasta p, luego cero) |
A R(p) |
PACF con corte brusco; ACF decae lento |
MA(q) |
Corte brusco en lag q (significativo hasta q, luego cero) |
Decae gradualmente |
M A(q) |
ACF con corte brusco; PACF decae lento |
ARMA (p,q) |
Ambas decaen gradualmente (sin cortes bruscos) |
Ambas decaen gradualmente |
A RMA( p,q) |
Tanto ACF como PACF decaen lento/oscilar sin corte claro |
Esta ciona lidad pura |
Picos periódicos en múltiplos del periodo |
Picos o patrones oscilantes en múltiplos del periodo |
SA RIMA |
ACF y PACF con picos fijos (ej. cada 12 lags si mensual) |
Tend encia |
ACF decae muy lentamente, rara vez cerca de cero |
PACF s ignificativa solo en primeros lags, luego dispersión |
Apl icar di fere ncia |
ACF con caída lenta; indica no estacionariedad |
Tend encia y Esta ciona lidad |
ACF con caída lenta y picos periódicos |
PACF con corte brusco y patrones oscilantes |
Dif eren ciar y mod elar es taci onal idad |
Combinación de patrones de tendencia y estacionalidad en ACF y PACF |
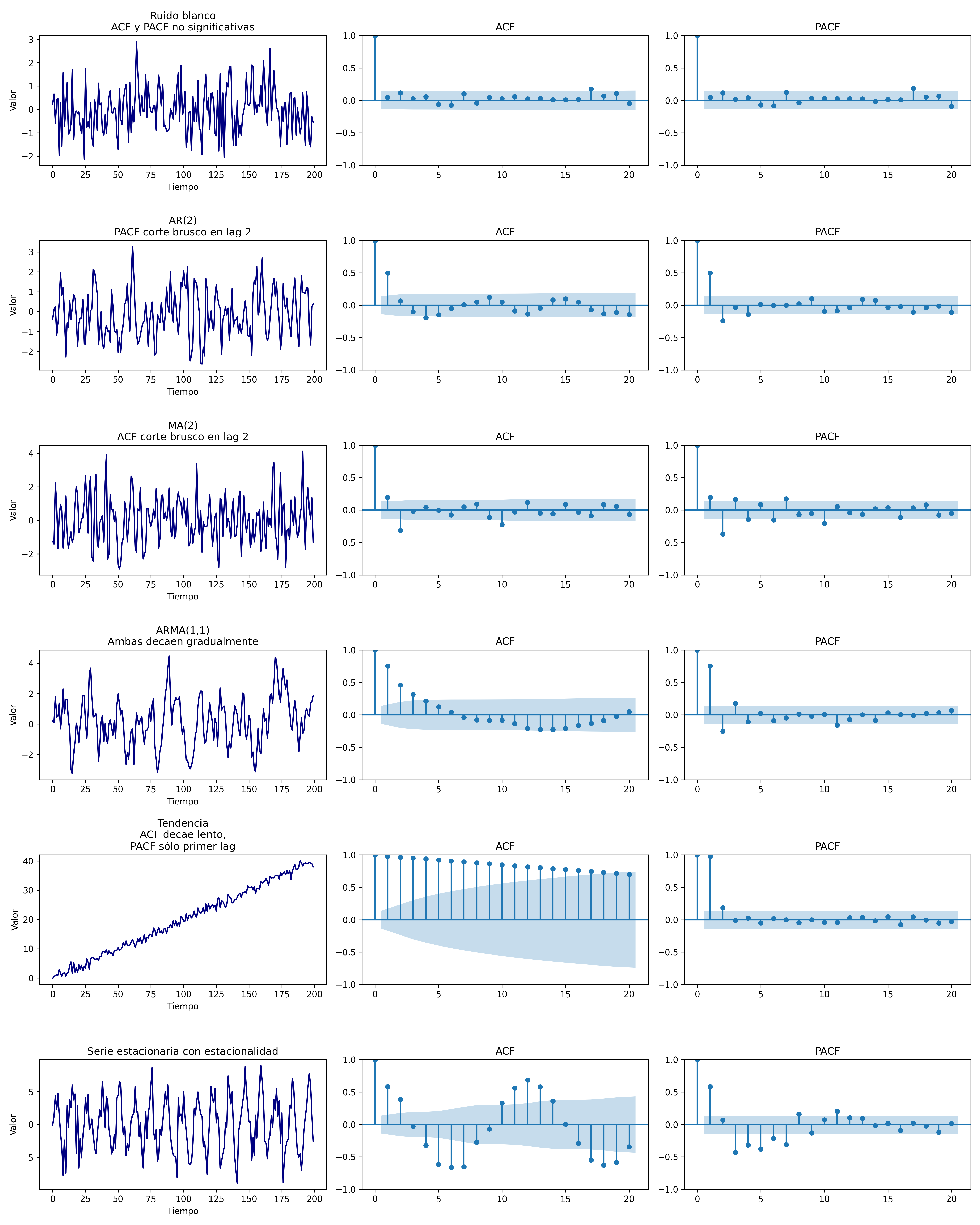
Gráficos_ACF_PACF#