Ejemplo pronóstico serie de tiempo#

En este ejemplo se hará el pronóstico a una serie de tiempo con una Red Neuronal Artificial Feedforward.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import yfinance as yf
import warnings

warnings.filterwarnings("ignore")

import tensorflow as tf

print(tf.__version__)

2.18.0

# Cargar los datos omitiendo la primera fila como encabezado y asignando nombres a las columnas
data = pd.read_csv("Irradiance_mensual.csv", skiprows=1, header=None,
                   names=["Fecha", "Irradiancia"])

# Convertir la columna 'Fecha' a datetime
data["Fecha"] = pd.to_datetime(data["Fecha"], format="%Y-%m")

# Set 'Fecha' as the index
data.set_index("Fecha", inplace=True)

plt.figure(figsize=(20, 5))  # Establecer el tamaño del gráfico
plt.plot(data.index, data["Irradiancia"], label="Irradiancia", color="blue")  # Dibujar los datos reales
plt.title("Irradiancia Mensual")  # Título del gráfico
plt.xlabel("Tiempo")  # Etiqueta del eje X
plt.ylabel("Irradiancia")  # Etiqueta del eje Y
plt.legend()  # Añadir leyenda para identificar las líneas
plt.show()

Pasos para el procesamiento de los datos antes de la Red Neuronal Artificial:

Conjunto de Train y Test.
Escalado de los datos: con Train se escala Test.
Creación de lags: los lags serán las X de entrada al modelo.

Conjunto de Train y Test:#

La división del dataset no debe hacerse igual que los problemas de regresión o clasificación, en este caso la secuencia de los datos es muy importante.

Los primeros datos, que son los más lejanos se usan como conjunto de train y los más reciente como conjunto de test.

En caso de dividir el dataset en tres conjuntos: train, validation y test, el conjunto de test siempre tiene los datos más recientes.

# Conjunto de test igual al último 20% de los datos:
test_size = int(len(data) * 0.2)
train, test = data[:-test_size], data[-test_size:]

# Graficar train y test:
plt.figure(figsize=(20, 5))
plt.plot(train.index, train["Irradiancia"], label="Train", color="blue")
plt.plot(test.index, test["Irradiancia"], label="Test", color="green")
plt.title("Conjunto de Train y Test")
plt.xlabel("Tiempo")
plt.ylabel("Irradiancia")
plt.legend()
plt.show()

La función train_test_split es útil para dividir arrays en subconjuntos. Sin embargo, en series temporales no se recomienda mezclar el orden de los datos (no hacer un shuffle), ya que se rompe la secuencia temporal. Por tanto, indicar shuffle=False.

# Usando librería de sklearn:
from sklearn.model_selection import train_test_split

train, test = train_test_split(data, test_size=0.2, shuffle=False)

Escalado de datos:#

from sklearn.preprocessing import MinMaxScaler

scaler = MinMaxScaler()
train_scaled = scaler.fit_transform(train)
test_scaled = scaler.transform(test)

# Graficar train_scaled y test_scaled:
plt.figure(figsize=(20, 5))
plt.plot(train.index, train_scaled, label="Train Scaled", color="blue")
plt.plot(test.index, test_scaled, label="Test Scaled", color="green")
plt.title("Conjunto de Train y Test Escalados")
plt.xlabel("Tiempo")
plt.ylabel("Irradiancia Escalada")
plt.legend()
plt.show()

Creación de los lags:#

# Función para crear los lags con entradas los valores y la cantidad de lags:
def prepare_data(precio, n_lags):
    X = []
    y = []
    for i in range(n_lags, len(precio)):

        lag_features = precio[i - n_lags : i, 0]  # Extraemos el vector de lags
        X.append(lag_features)
        # El target es el valor en la posición actual
        y.append(precio[i, 0])

    # Convertimos las listas a numpy.ndarray
    X = np.array(X)
    y = np.array(y)

    return X, y

lags = 3
X_train, y_train = prepare_data(train_scaled, lags)
X_test, y_test = prepare_data(test_scaled, lags)

print("Primeras 7 filas de train_scaled")
print(train_scaled[:7])
print("Primeras 7 filas de X_train")
print(X_train[:7])
print("Primeras 7 filas de y_train")
print(y_train[:7])

Primeras 7 filas de train_scaled
[[0.48740815]
 [0.70646554]
 [0.75676137]
 [0.94073235]
 [0.91909811]
 [0.58563094]
 [0.54581954]]
Primeras 7 filas de X_train
[[0.48740815 0.70646554 0.75676137]
 [0.70646554 0.75676137 0.94073235]
 [0.75676137 0.94073235 0.91909811]
 [0.94073235 0.91909811 0.58563094]
 [0.91909811 0.58563094 0.54581954]
 [0.58563094 0.54581954 0.53484075]
 [0.54581954 0.53484075 0.58408894]]
Primeras 7 filas de y_train
[0.94073235 0.91909811 0.58563094 0.54581954 0.53484075 0.58408894
 0.41556642]

print("Primeras 7 filas de test_scaled")
print(test_scaled[:7])
print("Primeras 7 filas de X_test")
print(X_test[:7])
print("Primeras 7 filas de y_test")
print(y_test[:7])

Primeras 7 filas de test_scaled
[[0.69685772]
 [0.45709393]
 [0.47749527]
 [0.65689354]
 [0.72275912]
 [0.77125762]
 [0.63123019]]
Primeras 7 filas de X_test
[[0.69685772 0.45709393 0.47749527]
 [0.45709393 0.47749527 0.65689354]
 [0.47749527 0.65689354 0.72275912]
 [0.65689354 0.72275912 0.77125762]
 [0.72275912 0.77125762 0.63123019]
 [0.77125762 0.63123019 0.33157341]
 [0.63123019 0.33157341 0.20916178]]
Primeras 7 filas de y_test
[0.65689354 0.72275912 0.77125762 0.63123019 0.33157341 0.20916178
 0.34457741]

print("Forma de X_train:", X_train.shape)
print("Forma de y_train:", y_train.shape)
print("Forma de X_test:", X_test.shape)
print("Forma de y_test:", y_test.shape)
print("Forma de serie de tiempo", data.shape)

Forma de X_train: (383, 3)
Forma de y_train: (383,)
Forma de X_test: (94, 3)
Forma de y_test: (94,)
Forma de serie de tiempo (483, 1)

Red Neuronal Artificial en Keras:#

from keras.models import Sequential
from keras.layers import Dense

# Creación del modelo:

model = Sequential()
model.add(Dense(22, activation="tanh", input_shape=(X_train.shape[1],)))
model.add(Dense(22, activation="tanh"))
model.add(Dense(1))
model.compile(optimizer="adam", loss="mse")

model.summary()

Model: "sequential"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type)                         ┃ Output Shape                ┃         Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ dense (Dense)                        │ (None, 22)                  │              88 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_1 (Dense)                      │ (None, 22)                  │             506 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_2 (Dense)                      │ (None, 1)                   │              23 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘

 Total params: 617 (2.41 KB)

 Trainable params: 617 (2.41 KB)

 Non-trainable params: 0 (0.00 B)

Primera capa: Hay tres variables de entrada (3 lags) que van para 22 neuronas. Los parámetros son: 22 * 3 + 22. El último 22 es el Bias (uno por cada neurona). Para un total de 88 pesos o parámetros entrenables.

Segunda capa: De la primera capa que tiene 22 neuronas salen 22 variables. Los parámetros son: 22 * 22 + 22 = 506 parámetros entrenables.

Tercera capa: De la primera capa que tiene 22 neuronas salen 22 variables y cómo esta capa sólo tiene una neurona, entonces, los parámetros entrenables son: 22 + 1 = 23.

# Entrenamiento del modelo:

history = model.fit(
    X_train,
    y_train,
    epochs=200,
    batch_size=64,
    validation_data=(X_test, y_test),
    verbose=0,
)

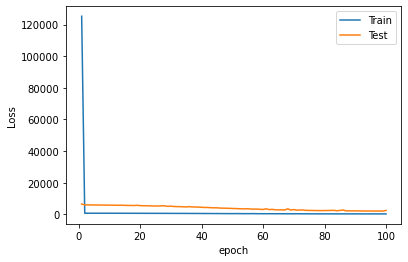
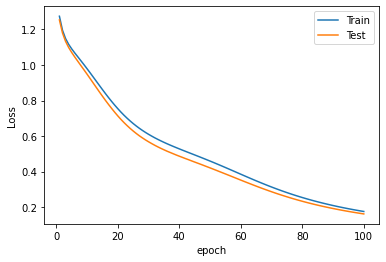
# Gráfica de Loss:

plt.plot(history.history["loss"], label="Train Loss")
plt.plot(history.history["val_loss"], label="Test Loss")
plt.title("Loss del Modelo")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend()
plt.show()

# Pronóstico sobre X_train y X_test:

y_train_pred = model.predict(X_train, verbose=0)
y_test_pred = model.predict(X_test, verbose=0)

# Devolver el escalado:
y_train_pred_real = scaler.inverse_transform(y_train_pred)
y_test_pred_real = scaler.inverse_transform(y_test_pred)

plt.figure(figsize=(20, 5))
plt.plot(train.index, train["Irradiancia"], label="Train", color="blue")
plt.plot(test.index, test["Irradiancia"], label="Test", color="green")
plt.plot(
    train[lags : train.shape[0]].index,
    y_train_pred_real,
    label="Train Pred",
    color="red",
)
plt.plot(
    test[lags : test.shape[0]].index, y_test_pred_real, label="Test Pred", color="red"
)
plt.axvline(
    x=train.index[-1], color="gray", linestyle="--", label="Inicio del Pronóstico"
)
plt.title("Conjunto de Train y Test")
plt.xlabel("Tiempo")
plt.ylabel("Irradiancia")
plt.legend()
plt.show()

# Evaluación del desempeño con MSE y R cuadrado:

from sklearn.metrics import mean_squared_error, r2_score

mse_train = mean_squared_error(train_scaled[lags:], y_train_pred)
mse_test = mean_squared_error(test_scaled[lags:], y_test_pred)
r2_train = r2_score(y_train, y_train_pred)
r2_test = r2_score(y_test, y_test_pred)

print("MSE Train:", mse_train)
print("MSE Test:", mse_test)
print("R cuadrado Train:", r2_train)
print("R cuadrado Test:", r2_test)

MSE Train: 0.020247441976006437
MSE Test: 0.014151724339594702
R cuadrado Train: 0.4093973100254159
R cuadrado Test: 0.34461958292064365

Análisis de Residuales:#

# Cálculo de los residuales:

residuals = y_train - y_train_pred.flatten()

# Gráfico de los residuales:
plt.scatter(
    train[lags : train.shape[0]].index, residuals, label="Residuos", color="blue"
)
plt.axhline(0, color="red", linestyle="--", label="Media de los Residuos")
plt.xlabel("Tiempo")
plt.ylabel("Residuos")
plt.legend()
plt.show()

# Prueba de normalidad de los residuales:

from scipy.stats import shapiro

stat, p = shapiro(residuals)

# Decir explícitamente si es normal o no:
alpha = 0.05
if p > alpha:
    print("Los residuales son normales (no se rechaza H0)")
else:
    print("Los residuales no son normales (se rechaza H0)")

Los residuales son normales (no se rechaza H0)

Pronóstico por fuera de la muestra:#

Una vez que el modelo ha sido entrenado y los residuales son satisfactorios, es posible realizar pronósticos más allá de los datos disponibles (pronóstico fuera de la muestra).

Este proceso se lleva a cabo de manera recursiva: se toma como punto de partida los últimos datos conocidos, los cuales se ingresan en la red entrenada para generar una predicción. Luego, el valor pronosticado se incorpora como una nueva entrada en el modelo para calcular el siguiente punto, y así sucesivamente.

n_forecast = 12 * 5  # Cantidad de fechas a pronosticar.

current_input = X_test[-1:]  # Se empieza con el últimos datos del conjunto de Test.

forecasted = []
predictions_out = []

for i in range(n_forecast):

    # Se predice el siguiente valor y se añade un residuo aleatorio
    next_value = (model.predict(current_input, verbose=0)[:, 0]
        + np.random.choice(residuals.flatten(), size=1, replace=True)[0])

    forecasted.append(next_value)

    # Actualizamos la entrada: desplazamos los lags y colocamos el valor predicho al final
    current_input = np.roll(current_input, -1)
    current_input[0, -1] = next_value

# Convertir la lista de predicciones a un array de forma (n_forecast, 1)
predictions_out = np.array(forecasted).reshape(-1, 1)

# Se devuelve el escalado a los valores pronosticados:
predictions_out = scaler.inverse_transform(predictions_out).flatten()

# Graficar el pronóstico por fuera de la muestra

forecast_index = pd.date_range(start=data.index[-1], periods=n_forecast + 1, freq="M")[
    1:
]  # Creación de las fechas futuras empezando desde el final de Test y frecuencia mensual


plt.figure(figsize=(20, 5))
plt.plot(train.index, train["Irradiancia"], label="Train", color="blue")
plt.plot(test.index, test["Irradiancia"], label="Test", color="green")
plt.plot(
    train[lags : train.shape[0]].index,
    y_train_pred_real,
    label="Train Pred",
    color="red",
)
plt.plot(
    test[lags : test.shape[0]].index, y_test_pred_real, label="Test Pred", color="red"
)
plt.axvline(
    x=train.index[-1], color="gray", linestyle="--", label="Inicio del Pronóstico"
)
plt.axvline(
    x=forecast_index[0],
    color="gray",
    linestyle="--",
    label="Inicio del Pronóstico Fuera de la Muestra",
)
plt.plot(
    forecast_index,
    predictions_out,
    label="Pronóstico por Fuera de Muestra",
    color="black",
)
plt.title("Conjunto de Train y Test")
plt.xlabel("Tiempo")
plt.ylabel("Irradiancia")
plt.legend()
plt.show()

Ejemplo pronóstico serie de tiempo

Contents