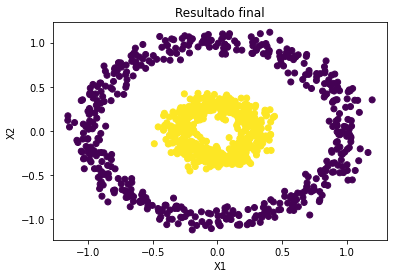
LSTM

Problema de Short-Term Memory:

Debido a las transformaciones que experimentan los datos cuando atraviesan una RNN, se pierde algo de información en cada paso de tiempo. Después de un tiempo, el estado de la RNN prácticamente no contiene rastro de las primeras entradas. Para abordar este problema, se han introducido varios tipos de celdas con memoria a largo plazo (Long Term). Han tenido tanto éxito que las celdas básicas ya no se usan mucho. La más popular de estas celdas de memoria a largo plazo: la celda LSTM.

LSTM cells:

La celda de memoria a corto y largo plazo (LSTM - Long Short-Term Memory) fue propuesta en 1997 y fue mejorada gradualmente a lo largo de los años por varios investigadores. Las celdas LSTM funcionará mucho mejor; el entrenamiento convergerá más rápido y detectará dependencias a largo plazo en los datos.

En Keras, simplemente puede usar la capa LSTM en lugar de la capa SimpleRNN:

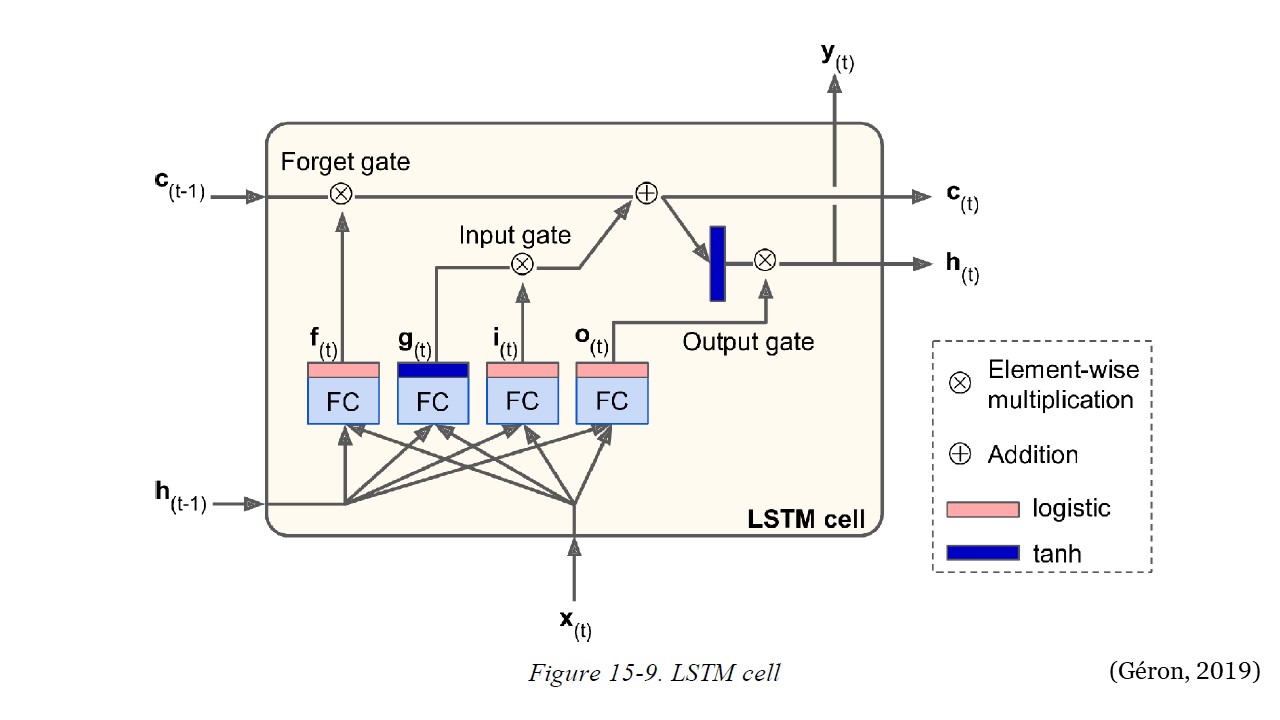
La arquitectura de LSTM se muestra en la siguiente figura. Si no mira lo que hay dentro de la caja, la celda LSTM se ve exactamente como una celda normal, excepto que su estado se divide en dos vectores: \(h_{(t)}\) y \(c_{(t)}\) (“c” significa “celda”). Puede pensar en \(h_{(t)}\) como el estado a corto plazo y en \(c_{(t)}\) como el estado a largo plazo.

LSTM

LSTM

La red aprende qué debe almacenar, qué desechar y qué leer del estado a largo plazo (\(c_{(t-1)}\)). El estado de largo plazo pasa por la red de izquierda a derecha y puede ver que primero pasa por una compuerta de olvido (forget gate), eliminando algunas memorias y luego agrega algunas memorias nuevas a través de la operación de suma que agrega las memorias que fueron seleccionadas por una puerta de entrada (input gate). Luego, el resultado \(c_{(t)}\) se envía directamente, sin más transformaciones.

De los anterior, en cada time step se eliminan algunos recuerdos y se agregan otros. Adicionalmente, después de la operación suma, el estado a largo plazo pasa por la función tanh, y luego el resultado es filtrado por la compuerta de salida (output gate). Esto produce el estado a corto plazo \(h_{(t)}\) que es igual a la salida de la celda para este time step, \(y_{(t)}\).

Nuevos recuerdos:

Los nuevos recuerdos vienen de la siguiente manera: primero, el vector de entradas \(x_{(t)}\) y el estado a corto plazo anterior \(h_{(t-1)}\) alimentan cuatro compuertas diferentes completamente conectadas. Estas compuertas tienen el siguiente propósito:

  • La compuerta principal es la que genera la salida \(g_{(t)}\). Esta compuerta analiza las entradas \(x_{(t)}\) y el estado a corto plazo anterior \(h_{(t-1)}\). Si la salida de esta compuerta es importante, se almacena en el estado a largo plazo.

  • Las otras tres compuertas son controladoras. Cada una tiene la función de activación logística (sigmoide) y las salidas van de 0 a 1. Estas tres salidas alimentan a operaciones de multiplicación, por lo que, si emiten 0, cierran la compuerta, o la abren si arrojan 1. Estas son las tres compuertas:

    • Compuerta de olvido (controlada por \(f_{(t)}\) - “f” de “forgot”): controla qué partes del estado a largo plazo (\(c_{(t-1)}\)) deben borrarse.

    • Compuerta de entrada (controlada por \(i_{(t)}\) - “i” de “input”): controla qué partes de \(g_{(t)}\) deben agregarse al estado a largo plazo (\(c_{(t-1)}\)).

    • Compuerta de salida (controlada por \(o_{(t)}\) - “o” de “output”): controla qué partes del estado a largo plazo (\(c_{(t-1)}\)) deben leerse y enviarse en este time step, tanto a \(h_{(t)}\) como a \(y_{(t)}\).

En resumen, una celda LSTM puede aprender a reconocer una entrada importante (ese es el papel de la puerta de entrada - input gate), almacenarla en el estado a largo plazo, conservarla durante el tiempo que sea necesario (ese es el papel de la puerta de olvido - forget gate) y extraerlo cuando sea necesario. Esto explica por qué estas celdas han tenido un éxito sorprendente al capturar patrones a largo plazo en series temporales, textos extensos, grabaciones de audio y más.

Las siguientes ecuaciones resumen cómo calcular el estado a largo plazo de la celda, su estado a corto plazo y su salida en cada time step para una sola instancia:

\[i_{(t)} = \sigma\left(W_{xi}^TX(t)+W_{hi}^Th_{(t-1)}+b_i\right)\]
\[f_{(t)} = \sigma\left(W_{xf}^TX(t)+W_{hf}^Th_{(t-1)}+b_f\right)\]
\[o_{(t)} = \sigma\left(W_{xo}^TX(t)+W_{ho}^Th_{(t-1)}+b_o\right)\]
\[g_{(t)} = tanh\left(W_{xg}^TX(t)+W_{hg}^Th_{(t-1)}+b_g\right)\]
\[c_{(t)} = f_{(t)} \times c_{(t-1)}+i_{(t)}\times g_{(t)}\]
\[y_{(t)} = h_{(t)} = o_{(t)} \times tanh\left(c_{(t-1)}\right)\]

Donde,

  • \(W_{xi}\), \(W_{xf}\), \(W_{xo}\), \(W_{xg}\) son las matrices de peso de cada una de las cuatro compuertas para su conexión con el vector de entrada \(x_{(t)}\).

  • \(W_{hi}\), \(W_{hf}\), \(W_{ho}\) y \(W_{hg}\) son las matrices de peso de cada una de las cuatro compuertas para su conexión con el estado anterior a corto plazo \(h_{(t-1)}\).

  • \(b_i\), \(b_f\), \(b_o\) y \(b_g\) son los términos de bias para cada una de las cuatro compuertas.

Código:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import yfinance as yf
from sklearn.preprocessing import StandardScaler
import warnings  # Para ignorar mensajes de advertencia

warnings.filterwarnings("ignore")

Descargar datos desde Yahoo Finance:

tickers = ["ES=F"]
ohlc = yf.download(tickers, period="max")
print(ohlc.tail())

[*******************100%*********************]  1 of 1 completed
               Open     High      Low    Close  Adj Close   Volume
Date
2022-08-24  4128.25  4158.50  4110.75  4142.75    4142.75  1348612
2022-08-25  4148.75  4202.75  4143.00  4201.00    4201.00  1635476
2022-08-26  4198.25  4217.25  4042.75  4059.50    4059.50  2241117
2022-08-29  4024.00  4064.00  4006.75  4031.25    4031.25  1963446
2022-08-30  4035.75  4072.75  3964.50  3987.50    3987.50  1963446
df = ohlc["Adj Close"].dropna(how="all")
df.tail()

Date
2022-08-24    4142.75
2022-08-25    4201.00
2022-08-26    4059.50
2022-08-29    4031.25
2022-08-30    3987.50
Name: Adj Close, dtype: float64

df = np.array(df[:, np.newaxis])
df.shape

(5548, 1)

plt.figure(figsize=(10, 6))
plt.plot(df)
plt.show()
../../../_images/output_19_02.png

Conjunto de train y test:

time_test = 0.10
train = df[: int(len(df) * (1 - time_test))]
test = df[int(len(df) * (1 - time_test)) :]

plt.plot(train)
plt.xlabel("Tiempo")
plt.ylabel("Precio")
plt.title("Conjunto de train")
plt.show()

plt.plot(test)
plt.xlabel("Tiempo")
plt.ylabel("Precio")
plt.title("Conjunto de test")
plt.show()
../../../_images/output_22_03.png ../../../_images/output_22_11.png

Función para conformar el dataset para datos secuenciales:

def split_sequence(sequence, time_step):
    X, y = list(), list()
    for i in range(len(sequence)):
        end_ix = i + time_step
        if end_ix > len(sequence) - 1:
            break
        seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
        X.append(seq_x)
        y.append(seq_y)
    return np.array(X), np.array(y)

time_step = 10

X_train, y_train = split_sequence(train, time_step)
X_test, y_test = split_sequence(test, time_step)

X_train.shape

(4983, 10, 1)

X_test.shape

(545, 10, 1)

Arquitectura de la red con celdas LSTM:

from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
import keras

import time

StartTime = time.time()

model = Sequential()
model.add(LSTM(100, activation="selu", input_shape=(time_step, 1), return_sequences=True))
model.add(LSTM(100, activation="selu"))
model.add(Dense(1))
model.compile(optimizer="adam", loss="mse")
history = model.fit(
    X_train,
    y_train,
    validation_data=(X_test, y_test),
    epochs=200,
    batch_size=50,
    verbose=0
)

EndTime = time.time()
print("---------> Tiempo en procesar: ", round((EndTime - StartTime) / 60), "Minutos")

---------> Tiempo en procesar:  5 Minutos

Evaluación del desempeño:

mse = model.evaluate(X_test, y_test, verbose=0)
mse

4982.865234375

rmse = mse ** 0.5
rmse

70.58941304738977

plt.plot(range(1, len(history.epoch) + 1), history.history["loss"], label="Train")
plt.plot(range(1, len(history.epoch) + 1), history.history["val_loss"], label="Test")
plt.xlabel("epoch")
plt.ylabel("Loss")
plt.legend();
../../../_images/output_34_01.png

Predicción del modelo:

X_new = np.array(df[-time_step:]).reshape((1, time_step, 1))
X_new.shape

(1, 10, 1)

model.predict(X_new, verbose=0)

array([[4114.294]], dtype=float32)

y_pred = model.predict(X_test, verbose=0)
y_pred[0:5]

array([[3126.9236],
       [3128.2053],
       [3145.6504],
       [3149.2354],
       [3171.992 ]], dtype=float32)

plt.figure(figsize=(18, 6))
plt.plot(
    range(1, len(X_test) + 1),
    test[time_step:, :],
    color="b",
    marker=".",
    linestyle="-",
    label="True"
)
plt.plot(
    range(1, len(X_test) + 1),
    y_pred,
    color="g",
    marker=".",
    linestyle="-",
    label="y_pred"
)
plt.legend();
../../../_images/output_39_02.png

Predicción fuera de la muestra:

predictions = []

time_prediction = 20  # cantidad de predicciones fuera de la muestra

first_sample = df[-time_step:, 0]                             # última muestra dentro de la serie de tiempo
current_batch = first_sample[np.newaxis]                      # Transformación en muestras y time step
current_batch = np.reshape(current_batch, (1, time_step, 1))  # Transformación en 3D

for i in range(time_prediction):

    current_pred = model.predict(current_batch, verbose=0)[0]

    # Guardar la predicción
    predictions.append(current_pred)

    # Actualizar el lote para incluir ahora la predicción y soltar el primer valor (primer time step)
    current_batch = np.append(current_batch[:, 1:], [[current_pred]])[np.newaxis]
    current_batch = np.reshape(current_batch, (1, time_step, 1))  # Transformación en 3D

plt.figure(figsize=(10, 6))
plt.plot(
    range(1, len(df[-100:, 0]) + 1),
    df[-100:, 0],
    color="b",
    marker=".",
    linestyle="-",
    label="True"
)
plt.plot(
    range(len(df[-100:, 0]) + 1, len(df[-100:, 0]) + len(predictions) + 1),
    predictions,
    color="g",
    marker=".",
    linestyle="-",
    label="y_pred fuera de la muestra"
)
plt.legend();
../../../_images/output_42_01.png