Autocorrelación-ACF

La autocorrelación mide la relación lineal entre los valores de una serie de tiempo y sus propios valores en rezagos anteriores. Es fundamental para identificar patrones de dependencia temporal, detectar estacionalidad, tendencia y para decidir la transformación adecuada antes de modelar.

Correlación y Autocorrelación

La correlación mide la fuerza de la relación lineal entre dos variables distintas, \(x\) e \(y\):

\[r = \frac{\sum_{t=1}^N (x_t - \bar{x})(y_t - \bar{y})}{\sqrt{\sum_{t=1}^N (x_t - \bar{x})^2} \sqrt{\sum_{t=1}^N (y_t - \bar{y})^2}}\]

En las series de tiempo, como solo tenemos una variable, calculamos la correlación de la serie consigo misma en distintos rezagos. Esta es la autocorrelación.

Definición de Autocorrelación

Para una serie de tiempo \(\{y_t\}\) de longitud \(N\), el coeficiente de autocorrelación en el rezago \(k\) se define como:

\[\rho_k = \frac{\sum_{t=k+1}^N (y_t - \bar{y})(y_{t-k} - \bar{y})}{\sum_{t=1}^N (y_t - \bar{y})^2}\]

• \(\rho_k\) toma valores entre \(-1\) y \(1\).

• Si \(\rho_k \approx 1\): alta correlación positiva con el pasado.

• Si \(\rho_k \approx -1\): correlación negativa, la serie tiende a oscilar.

• Si \(\rho_k \approx 0\): no hay relación lineal con el pasado (posible ruido blanco).

Función de Autocorrelación (ACF)

El gráfico de la autocorrelación para distintos rezagos \(k\) se llama Función de Autocorrelación (ACF) o correlograma.

La ACF permite visualizar si existe dependencia a distintos rezagos:

• Valores altos en pequeños rezagos indican persistencia o tendencia.

• Picos en múltiplos de un periodo sugieren estacionalidad.

Interpretación de la ACF según el comportamiento de la serie

• Serie con tendencia: la ACF decae lentamente a medida que el rezago aumenta.

• Serie estacionaria: la ACF cae rápidamente a cero (usualmente después de uno o dos rezagos).

• Serie estacional: la ACF muestra picos en los rezagos correspondientes al periodo estacional (ej. 12 para datos mensuales con estacionalidad anual).

• Ruido blanco: todos los coeficientes de autocorrelación están cerca de cero.

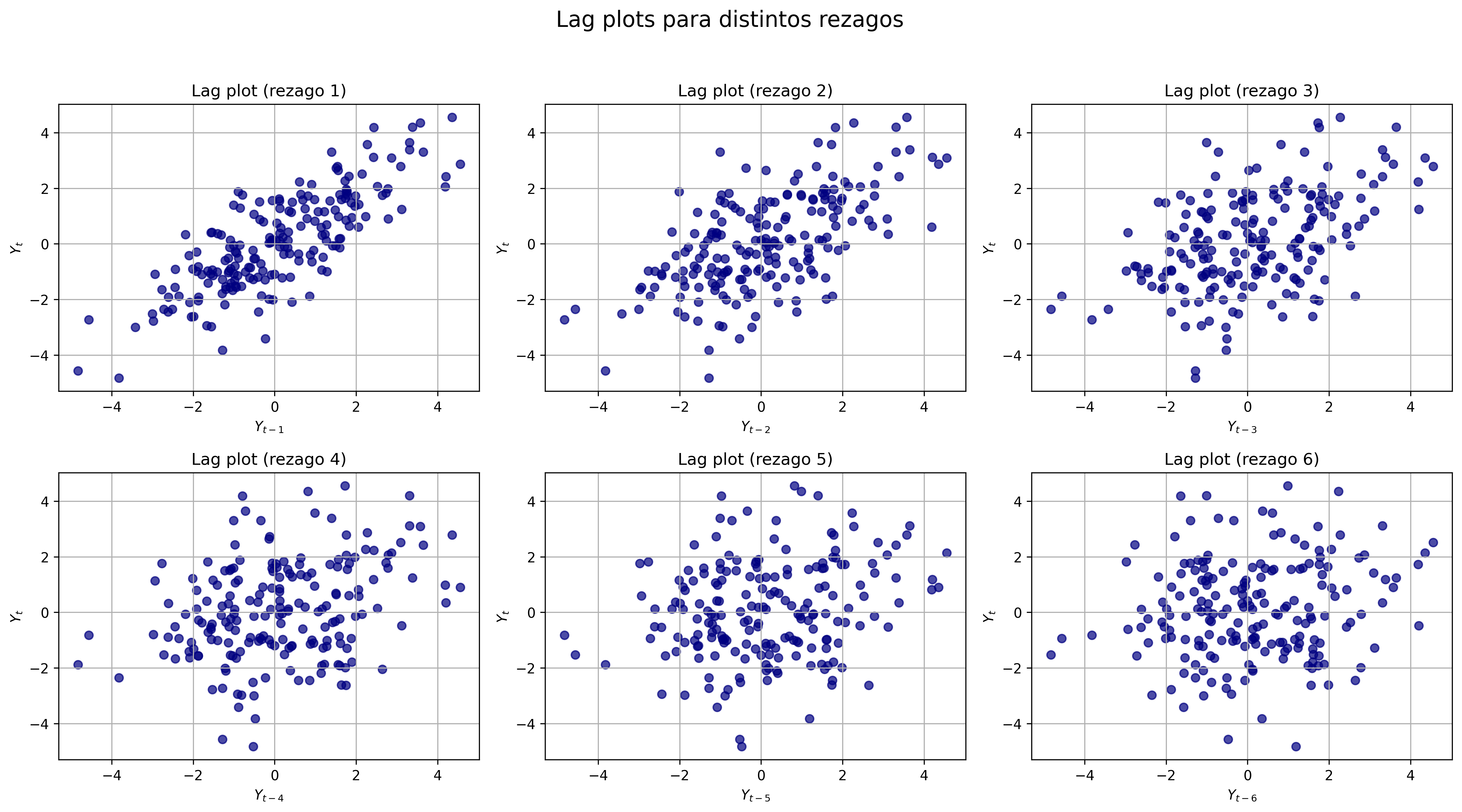
lag_plots

Comportamiento de la ACF

1. Caída rápida a cero

• Descripción: Los valores de la ACF caen bruscamente después de uno o dos rezagos.

• Implicación: La serie es estacionaria y no muestra dependencia significativa más allá de rezagos cortos. Es típica de series ruido blanco o procesos MA(q) puros.

• Recomendación: Se puede modelar sin diferenciación, modelos MA suelen funcionar bien.

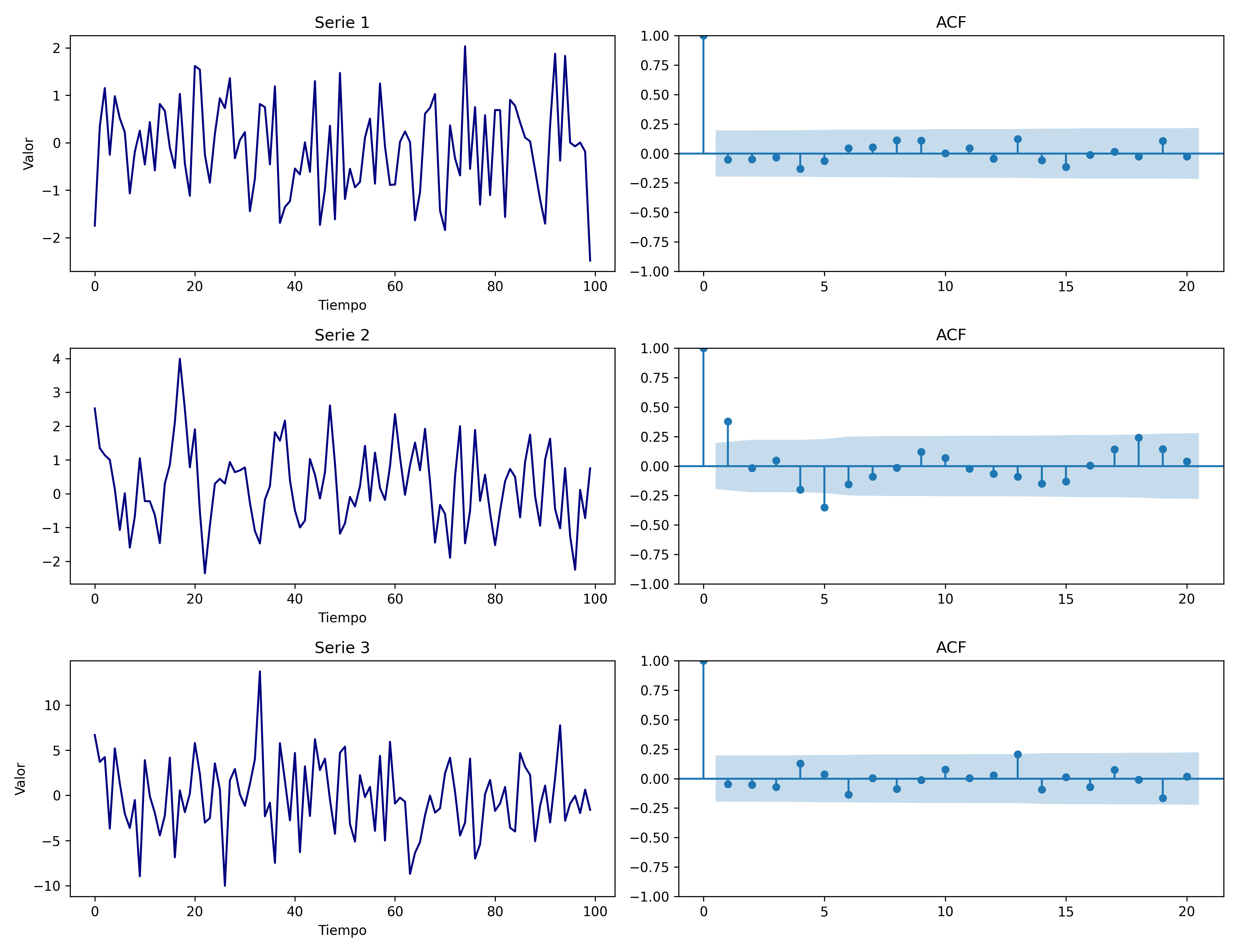
ACF_caída_rápida

2. Caída lenta (exponencial o lineal)

• Descripción: La ACF decrece gradualmente y tarda muchos rezagos en acercarse a cero.

• Implicación: Hay tendencia (no estacionariedad en media). El pasado influye por mucho tiempo.

• Recomendación: Aplicar diferenciación para eliminar la tendencia y obtener una serie estacionaria.

• Ejemplo típico: Serie con tendencia determinística.

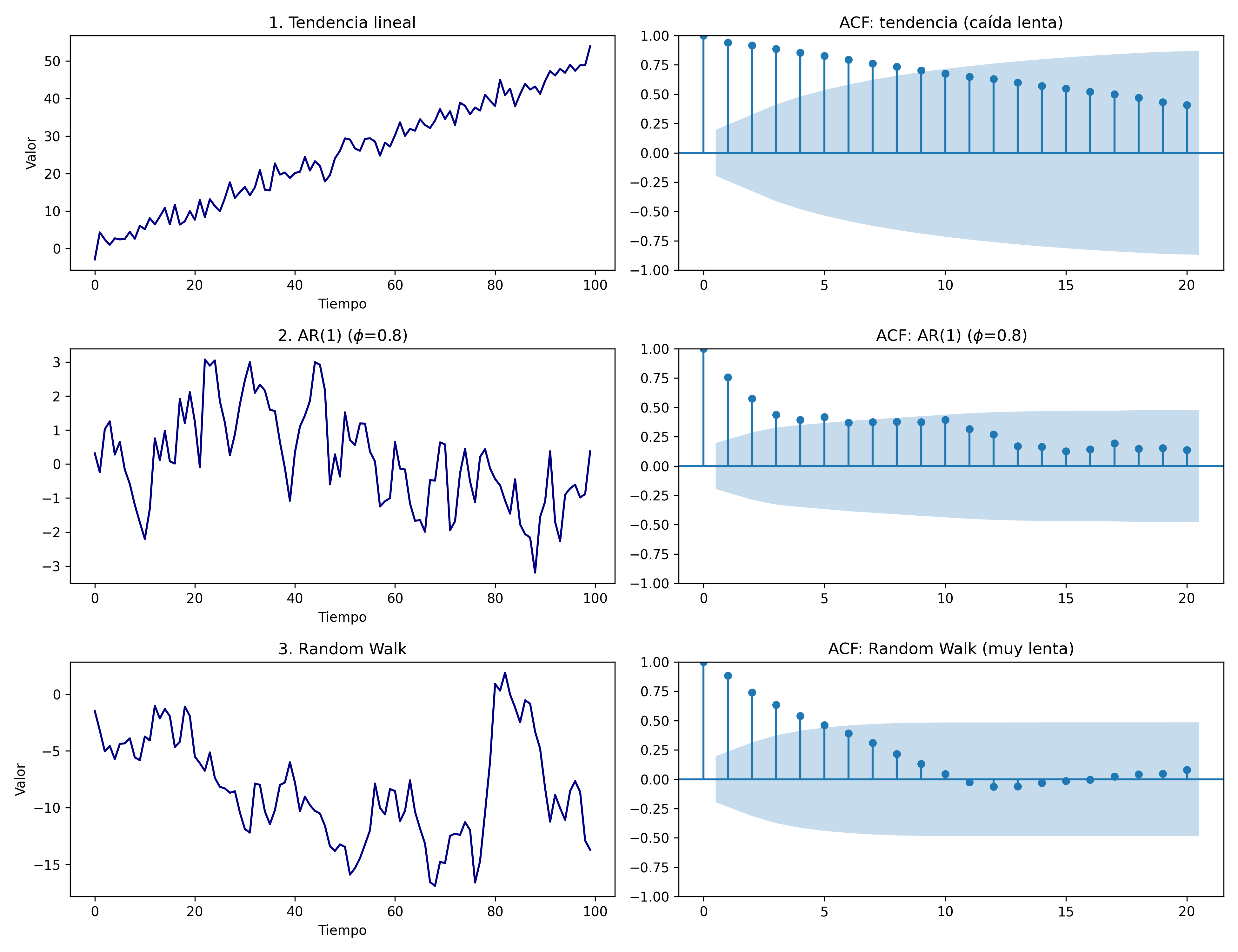
ACF_caída_lenta

3. Oscilación o patrón sinusoidal

• Descripción: La ACF alterna entre valores positivos y negativos de forma periódica, similar a una onda seno.

• Implicación: Puede indicar un proceso AR(2), o la presencia de ciclos, pero sin estacionalidad regular.

• Recomendación: Considerar modelos AR(2) o analizar la estructura de ciclos.

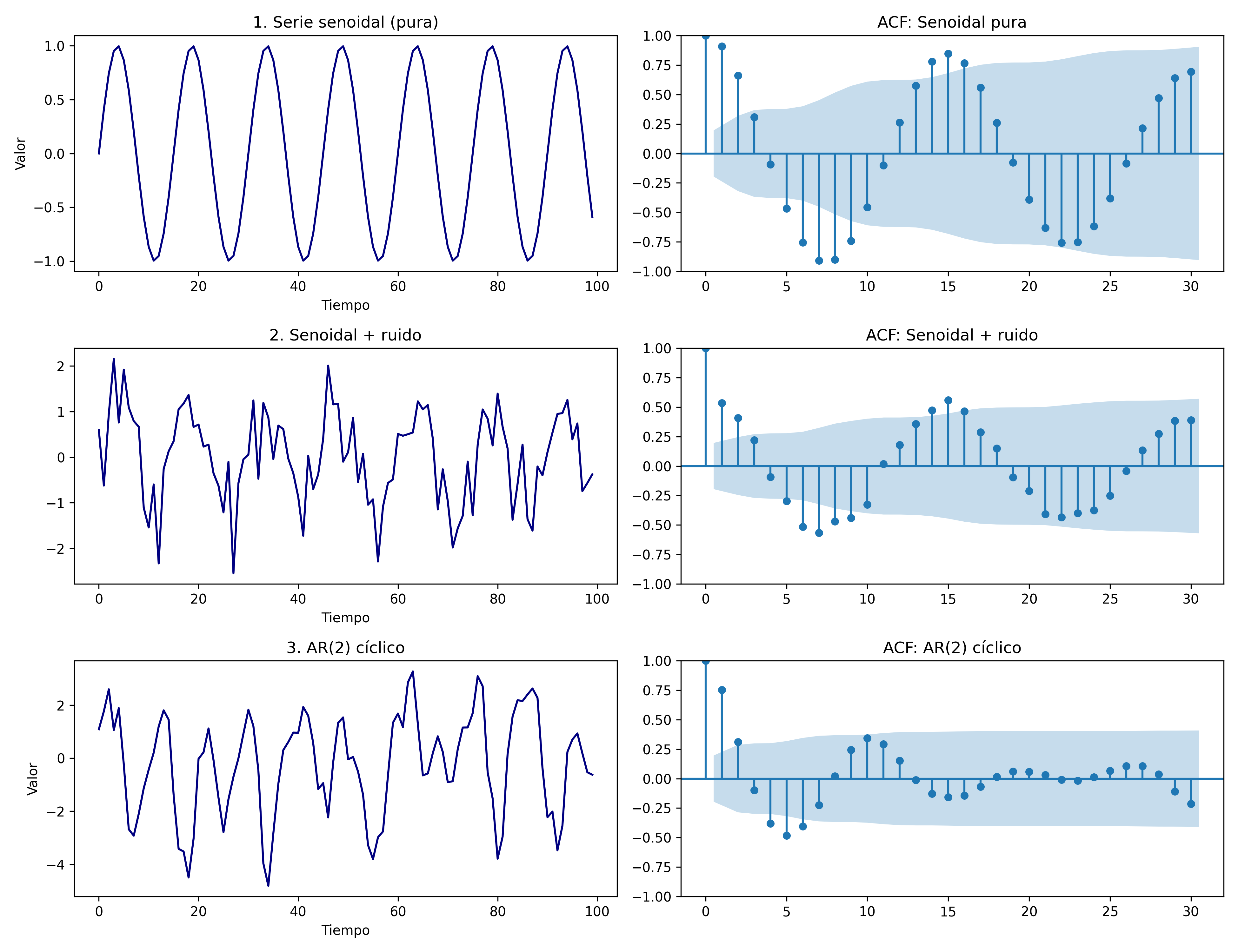
ACF_ciclico

4. Picos periódicos (patrón de dientes de sierra)

• Descripción: La ACF muestra picos claramente alineados con múltiplos de un periodo (por ejemplo, lags 12, 24, 36 en series mensuales).

• Implicación: Hay estacionalidad en la serie.

• Recomendación: Incluir términos estacionales en el modelo (por ejemplo, diferenciación estacional, SARIMA, o usar modelos con componentes estacionales explícitos).

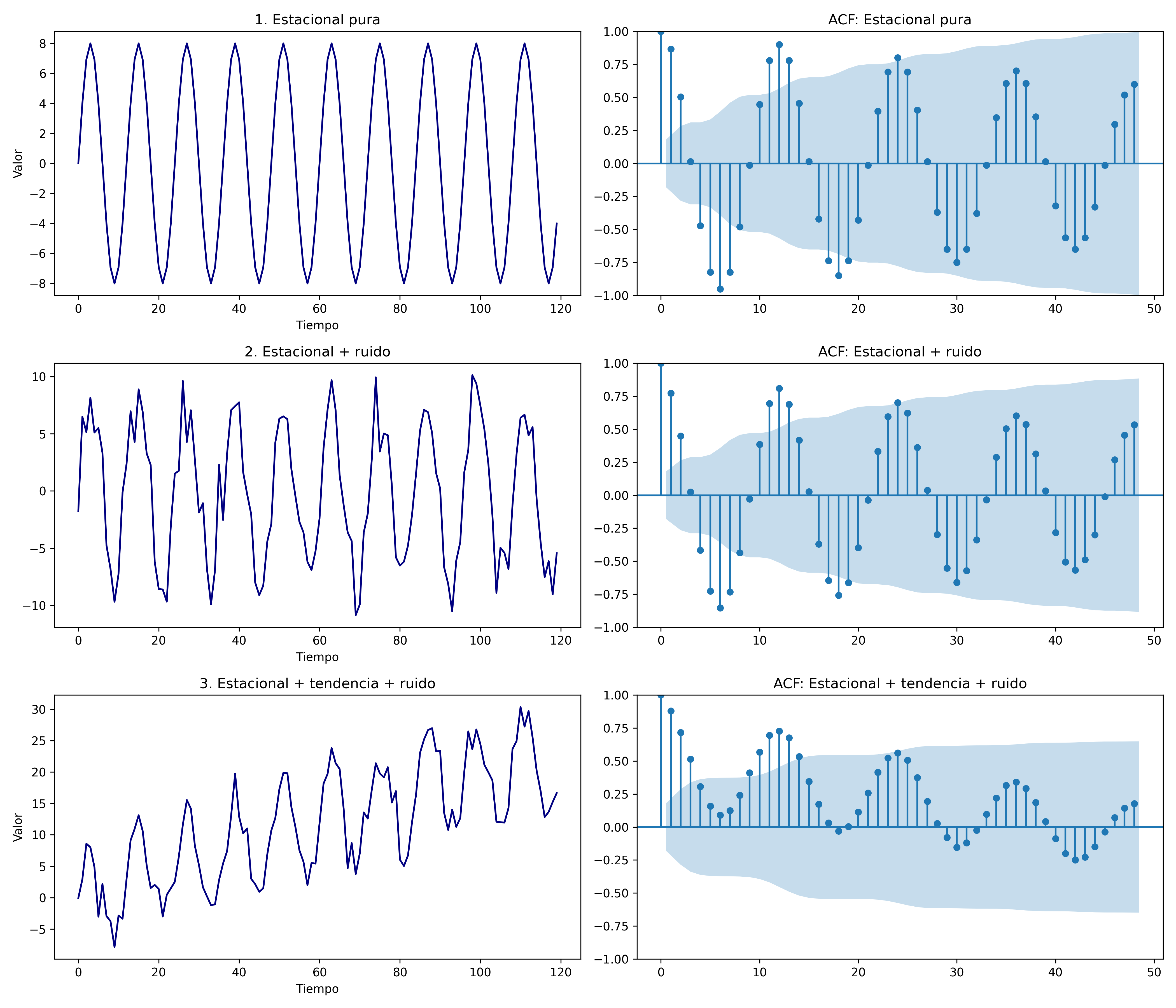
ACF_estacional

5. Ruido blanco

• Descripción: Los valores de la ACF están cerca de cero para todos los rezagos (excepto \(k=0\)).

• Implicación: La serie no tiene memoria, es completamente aleatoria.

• Recomendación: No es necesario modelar, no hay patrones predictivos.

6. Caída exponencial amortiguada con oscilaciones

• Descripción: La ACF decae de manera exponencial, pero alterna signos (positivo-negativo) y se va acercando a cero.

• Implicación: Indica un proceso ARMA o AR (ciclos amortiguados).

• Recomendación: Considerar modelos ARMA o AR con términos cíclicos.

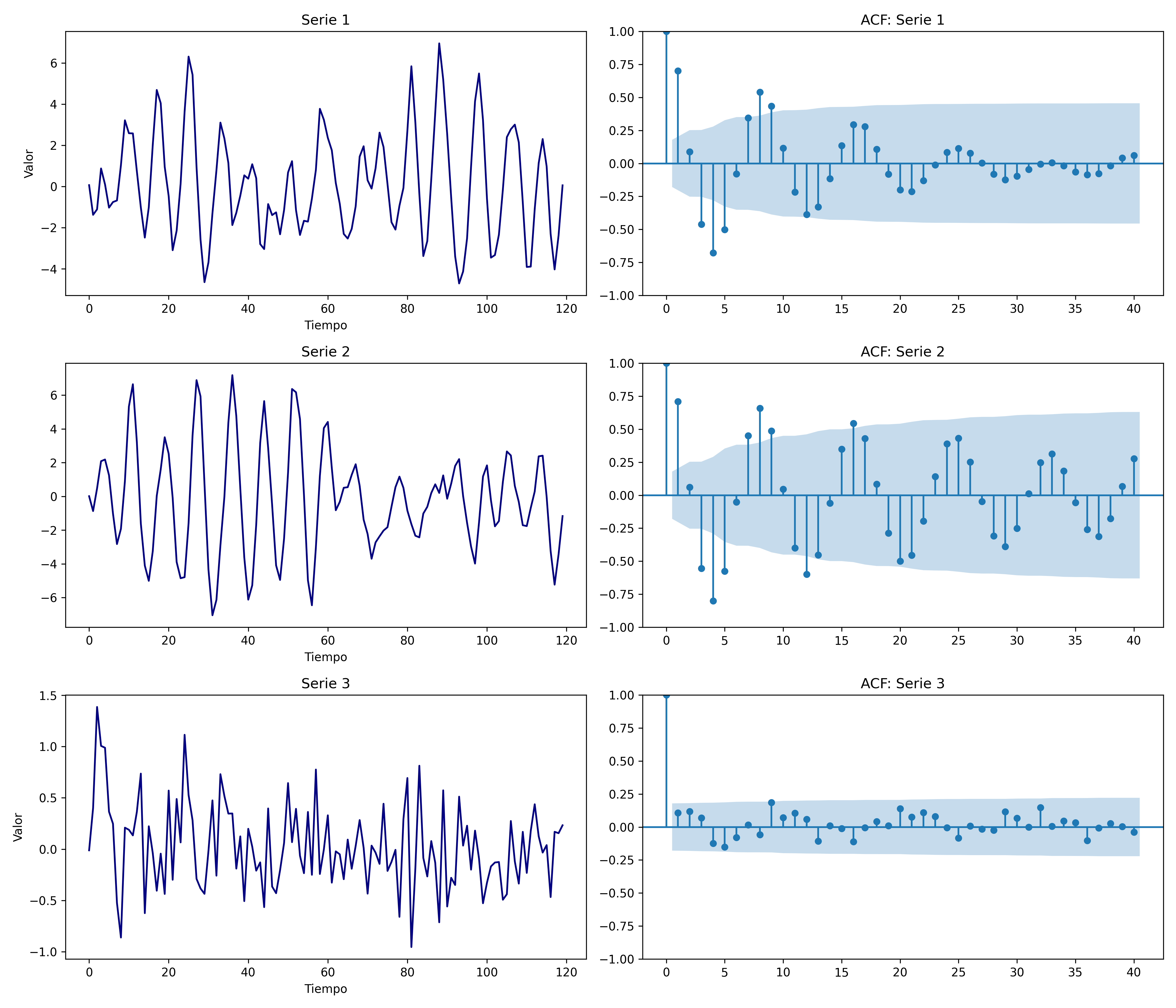
ACF_amortiguado

Resumen visual de patrones de la ACF

Patrón ACF	Diagnóstico	Sugerencia de modelo
Caída rápida a cero	Estacionaria / MA	MA, ARMA
Caída lenta	Tendencia	Diferenciación + ARMA
Oscilación (sin picos fijos)	Ciclos/AR(2)	AR(2), ARMA
Picos periódicos	Estacionalidad	SARIMA, modelos estacionales
Cerca de cero (excepto k=0)	Ruido blanco	Ningún modelo (o solo media)
Caída exponencial amortiguada	Ciclos amortiguados	ARMA con raíces complejas

Nota:

El análisis de la ACF debe complementarse con la PACF (Función de Autocorrelación Parcial), la inspección visual de la serie y pruebas de estacionariedad (ADF, KPSS). La ACF es tu “primer mapa” para saber cómo abordar la modelación.

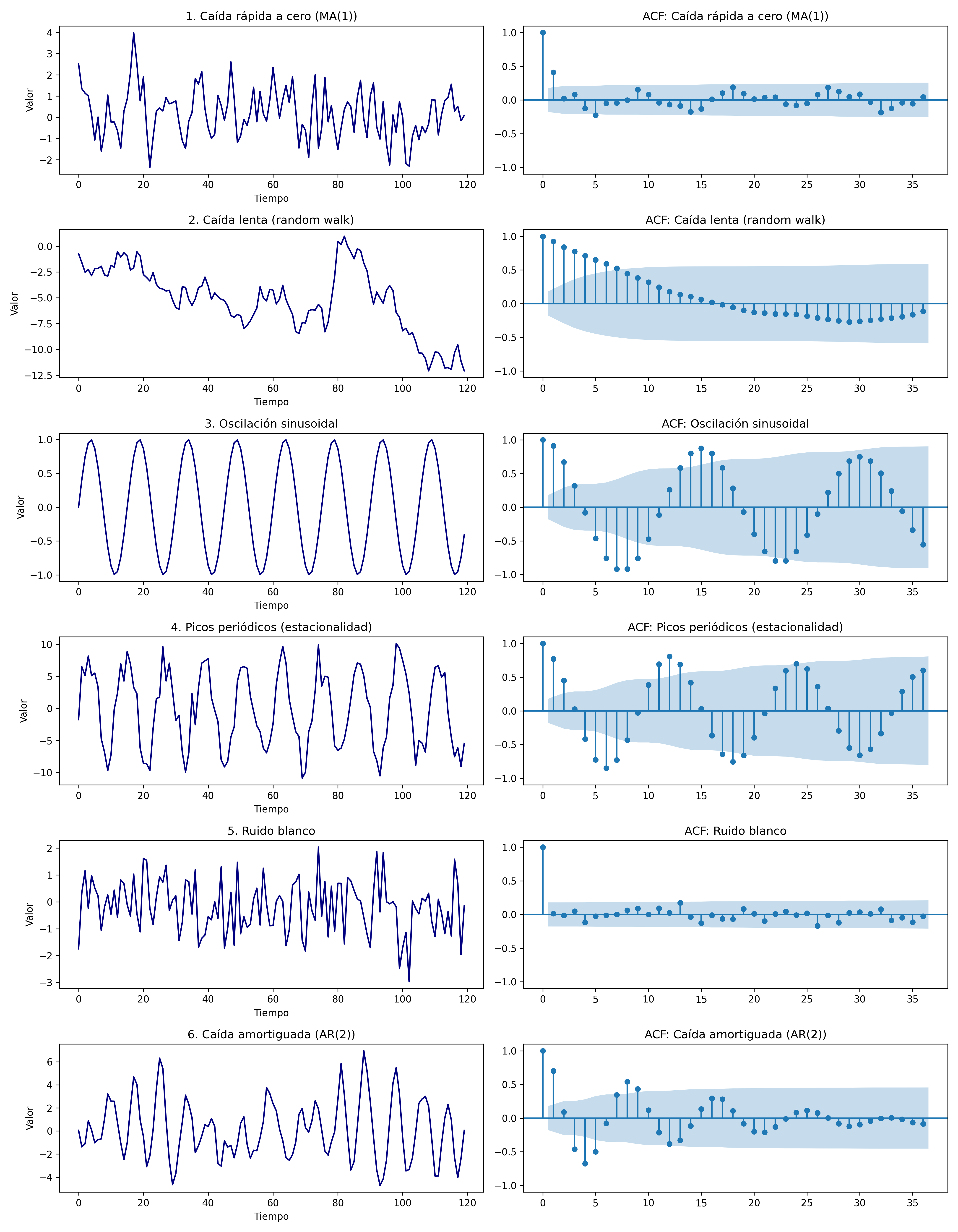
ACF_varios_patrones

Ruido blanco:

El ruido blanco (white noise) es un proceso estocástico fundamental en el análisis de series de tiempo. Se define como una secuencia de variables aleatorias independientes e idénticamente distribuidas (i.i.d.) con media cero y varianza constante \(\sigma^2\). Matemáticamente:

\[\varepsilon_t \sim \text{i.i.d.}~(0, \sigma^2)\]

• Media: \(E[\varepsilon_t] = 0\)

• Varianza: \(Var(\varepsilon_t) = \sigma^2 < \infty\)

• Independencia: \(Cov(\varepsilon_t, \varepsilon_{t-h}) = 0\) para todo \(h \neq 0\)

Propiedades del ruido blanco

• No tiene memoria: No existe correlación entre el valor actual y cualquier otro en el pasado o futuro.

• No muestra tendencia ni estacionalidad.

• Gráficamente, el ruido blanco es impredecible y fluctúa aleatoriamente alrededor de su media.

• La función de autocorrelación (ACF) muestra todos los coeficientes cercanos a cero, excepto en el rezago 0 (donde es igual a 1).

Importancia y usos del ruido blanco en series de tiempo

1. Modelo de referencia (benchmark):

   El ruido blanco es el proceso más simple posible. Se utiliza como línea base para comparar si una serie tiene estructura temporal relevante o simplemente es aleatoria.

2. Diagnóstico de modelos:

   En el modelado de series de tiempo (ARMA, ARIMA, SARIMA, etc.), el objetivo es que los residuos (“errores”) del modelo se comporten como ruido blanco.

   • Si los residuos son ruido blanco, significa que el modelo ha capturado toda la estructura predecible.

   • Si no, hay patrones sin modelar (posible mala especificación del modelo).

3. Pruebas de aleatoriedad:

   Pruebas estadísticas como la de Ljung-Box o de autocorrelación de residuos se usan para verificar si los residuos son ruido blanco.

4. Simulación y validación:

   El ruido blanco se usa como “ingrediente base” en la simulación de procesos ARMA/ARIMA, donde las series se generan agregando ruido blanco a la estructura autorregresiva/media móvil.

Pruebas estadísticas aplicadas a la ACF: ¿La serie es ruido blanco?

¿Para qué sirven las pruebas sobre la ACF?

Al analizar la Función de Autocorrelación (ACF) de una serie o de los residuos de un modelo, es fundamental determinar si:

• Las autocorrelaciones son estadísticamente diferentes de cero

• La serie es ruido blanco (sin patrones temporales), o

• Existe dependencia temporal (queda estructura por modelar)

1. Prueba de significancia individual de la ACF

• Bajo la hipótesis nula (H₀: la serie es ruido blanco), cada coeficiente de autocorrelación \(\hat{\rho}_k\) es aproximadamente normal con media cero y desviación estándar \(\frac{1}{\sqrt{N}}\).

• Por lo tanto, un valor está fuera del rango \(\pm 2/\sqrt{N}\) se considera significativo al 5% (aproximadamente).

• Limitación: esto es válido solo para pruebas individuales, no para muchos rezagos al tiempo.

2. Prueba global: Test de Ljung-Box (Q-statistic)

La prueba de Ljung-Box evalúa si un conjunto de \(h\) autocorrelaciones (por ejemplo, los primeros 10 o 20 lags) son colectivamente cero, es decir, si hay evidencia global de dependencia temporal.

Hipótesis:

• H₀: Todas las autocorrelaciones hasta el rezago \(h\) son cero (serie = ruido blanco)

• H₁: Alguna autocorrelación hasta el rezago \(h\) es diferente de cero

Estadístico:

\[Q = N(N+2) \sum_{k=1}^{h} \frac{\hat{\rho}_k^2}{N-k}\]

• \(N\) = tamaño de la muestra

• \(h\) = número de rezagos considerados

• \(\hat{\rho}_k\) = autocorrelación muestral en el lag \(k\)

Bajo \(H_0\), \(Q\) sigue aproximadamente una distribución \(\chi^2\) con \(h\) grados de libertad.

Interpretación:

• Si el p-valor es pequeño (\(<0.05\)), se rechaza \(H_0\): la serie no es ruido blanco (hay autocorrelación significativa).

• Si el p-valor es grande, no se rechaza \(H_0\): la serie puede considerarse ruido blanco.

3. Prueba de Box-Pierce

Es la versión original del test anterior, con estadístico más simple:

\[Q_{BP} = N \sum_{k=1}^{h} \hat{\rho}_k^2\]

Pero el test de Ljung-Box es preferido porque es más robusto, especialmente para muestras pequeñas.