Introducción a portafolios de inversión#

En esta clase, aprenderemos a descargar datos financieros utilizando Yahoo Finance, calcular los rendimientos, y analizar algunos aspectos básicos de las acciones de tres empresas: PFBCOLOM.CL, ISA.CL y CEMARGOS.CL. Utilizaremos Python para descargar los datos, graficar las series de tiempo y realizar análisis estadísticos que nos permitirán entender el comportamiento de estas acciones. Comenzaremos cubriendo los siguientes pasos:

Primero, necesitamos instalar la biblioteca yfinance:

pip install yfinance

Descargar datos de Yahoo Finance:#

import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt

# Definir las acciones y el período de tiempo
stocks = ['PFBCOLOM.CL', 'ISA.CL', 'CEMARGOS.CL']
start = '2019-11-01'

# Descargar los datos desde Yahoo Finance
data = yf.download(stocks, start=start, interval='1wk')['Adj Close'].dropna()
print("Cantidad de datos descargados: ", data.shape)
print(data)

[*******************100%*********************]  3 of 3 completed
Cantidad de datos descargados:  (262, 3)
            CEMARGOS.CL        ISA.CL   PFBCOLOM.CL
Date
2019-10-28  5263.764160  15392.110352  30526.080078
2019-11-04  4760.153320  15944.644531  31010.402344
2019-11-11  4760.153320  15502.617188  30858.181641
2019-11-18  4566.987793  14744.852539  30650.619141
2019-11-25  4394.518555  14839.574219  30014.082031
...                 ...           ...           ...
2024-09-30  7336.537109  17460.000000  32580.000000
2024-10-07  7465.075195  17500.000000  34200.000000
2024-10-14  7880.000000  18020.000000  35480.000000
2024-10-21  8200.000000  17900.000000  33920.000000
2024-10-28  8540.000000  17440.000000  35120.000000

[262 rows x 3 columns]

En este paso, descargamos los precios de cierre ajustados de las acciones durante los últimos 5 años. Los datos se almacenarán en un DataFrame de Pandas, donde cada columna corresponde a una acción.

# Cambiar el nombre de las columnas:

data.columns = ['CEMARGOS', 'ISA', 'PFBCOLOM']

Graficar los precios de las acciones:#

# Graficar los precios ajustados
plt.figure(figsize=(10, 6))
data.plot()
plt.title('Precios PFBCOLOM, ISA y CEMARGOS')
plt.xlabel('Fecha')
plt.ylabel('Precio de cierre ajustado')
plt.grid()
plt.show()

<Figure size 1000x600 with 0 Axes>

Calcular los rendimientos:#

\[Rendimiento = \frac{P_t}{P_{t-1}} -1\]

En Python, podemos calcular los rendimientos usando la función pct_change():

# Calcular los rendimientos
returns = data.pct_change().dropna()
print(returns.head())
print("Cantidad de datos de rendimientos: ", returns.shape)

            CEMARGOS       ISA  PFBCOLOM
Date
2019-11-04 -0.095675  0.035897  0.015866
2019-11-11  0.000000 -0.027723 -0.004909
2019-11-18 -0.040580 -0.048880 -0.006726
2019-11-25 -0.037764  0.006424 -0.020768
2019-12-02  0.012559 -0.015958  0.010143
Cantidad de datos de rendimientos:  (261, 3)

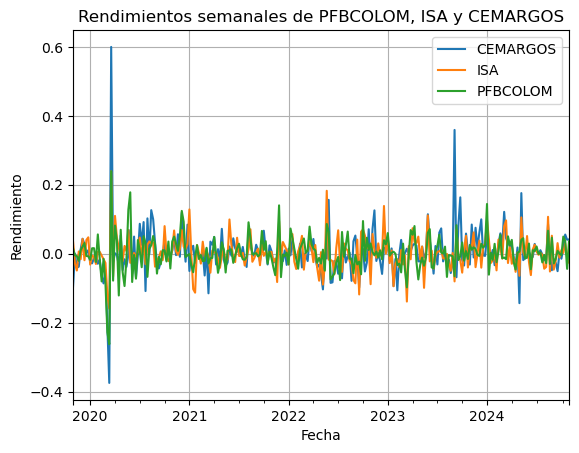
Graficar los rendimientos:#

Podemos graficar los rendimientos para tener una idea de su volatilidad a lo largo del tiempo.

# Graficar los rendimientos
plt.figure(figsize=(10, 6))
returns.plot()
plt.title('Rendimientos semanales de PFBCOLOM, ISA y CEMARGOS')
plt.xlabel('Fecha')
plt.ylabel('Rendimiento')
plt.grid()
plt.show()

<Figure size 1000x600 with 0 Axes>

Estadísticas básicas de los rendimientos:#

Vamos a calcular algunas estadísticas básicas como la media, desviación estándar, máximos y mínimos de los rendimientos.

# Calcular estadísticas básicas
stats_summary  = returns.describe()
print(stats_summary)

         CEMARGOS         ISA    PFBCOLOM
count  261.000000  261.000000  261.000000
mean     0.004117    0.001617    0.001819
std      0.069449    0.048094    0.050337
min     -0.375000   -0.159348   -0.262626
25%     -0.024775   -0.023454   -0.021465
50%     -0.001143    0.001692   -0.000732
75%      0.025896    0.025113    0.027407
max      0.600000    0.238806    0.239270

Rendimientos de cada acción:#

Vamos a calcular el rendimiento promedio de cada acción para evaluar su desempeño individual en el período analizado. Podemos hacer esto utilizando la función mean() de Pandas:

# Calcular el rendimiento promedio de cada acción
returns_stocks = returns.mean()
print(returns_stocks)

CEMARGOS    0.004117
ISA         0.001617
PFBCOLOM    0.001819
dtype: float64

Este cálculo nos permite conocer cuál de las acciones ha tenido el mejor rendimiento promedio durante el período.

Estos rendimientos son semanales.

Volatilidades:#

La volatilidad se define como la desviación estándar de los rendimientos:

# Calcular la volatilidad de cada acción
volatility = returns.std()
print(volatility)

CEMARGOS    0.069449
ISA         0.048094
PFBCOLOM    0.050337
dtype: float64

Estas volatilidades son semanales.

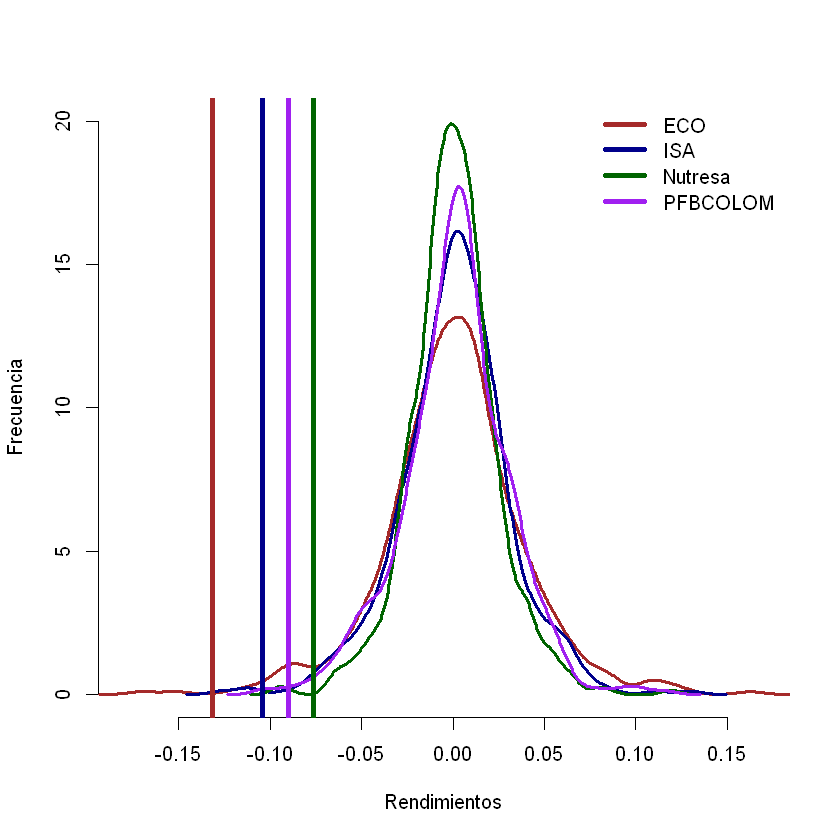
Histograma de los rendimientos:#

Podemos visualizar la distribución de los rendimientos mediante un histograma para observar cómo se distribuyen los valores.

Este histograma nos ayuda a identificar si los rendimientos siguen una distribución normal o presentan sesgos o kurtosis.

# Graficar el histograma de los rendimientos
returns.hist(bins=30, figsize=(10, 6))
plt.suptitle('Histograma de los rendimientos semanales de las acciones')
plt.show()

Matriz de Varianzas-Covarianzas:#

La matriz de varianzas-covarianzas muestra cómo los rendimientos de las diferentes acciones se mueven juntos.

# Calcular la matriz de varianzas-covarianzas
cov_matrix = returns.cov()
print(cov_matrix)

          CEMARGOS       ISA  PFBCOLOM
CEMARGOS  0.004823  0.001397  0.001707
ISA       0.001397  0.002313  0.001229
PFBCOLOM  0.001707  0.001229  0.002534

Matriz de Correlación:#

La matriz de correlación nos da una idea de la fuerza de la relación lineal entre los rendimientos de las diferentes acciones.

# Calcular la matriz de correlación
corr_matrix = returns.corr()
print(corr_matrix)

          CEMARGOS       ISA  PFBCOLOM
CEMARGOS  1.000000  0.418284  0.488352
ISA       0.418284  1.000000  0.507672
PFBCOLOM  0.488352  0.507672  1.000000

La matriz de correlación tiene valores entre -1 y 1. Valores cercanos a 1 indican una relación positiva fuerte, mientras que valores cercanos a -1 indican una relación negativa fuerte.

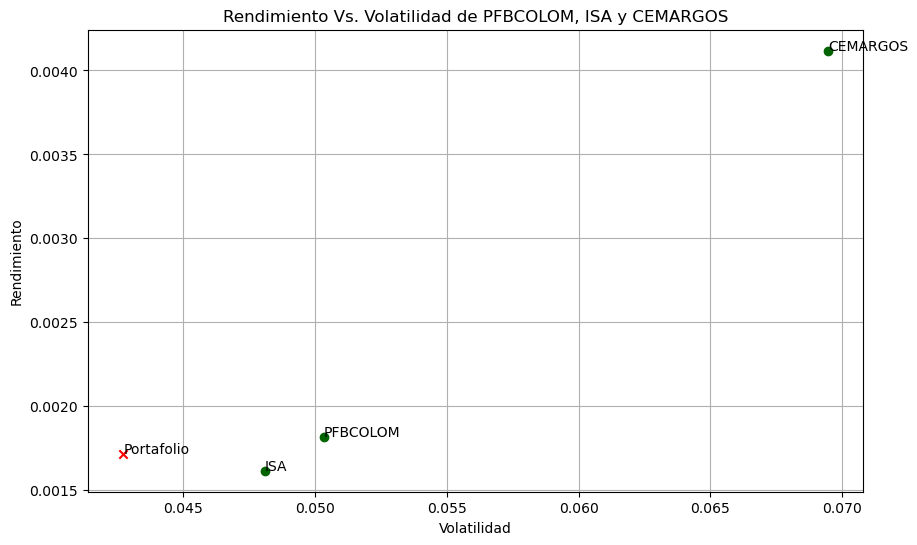
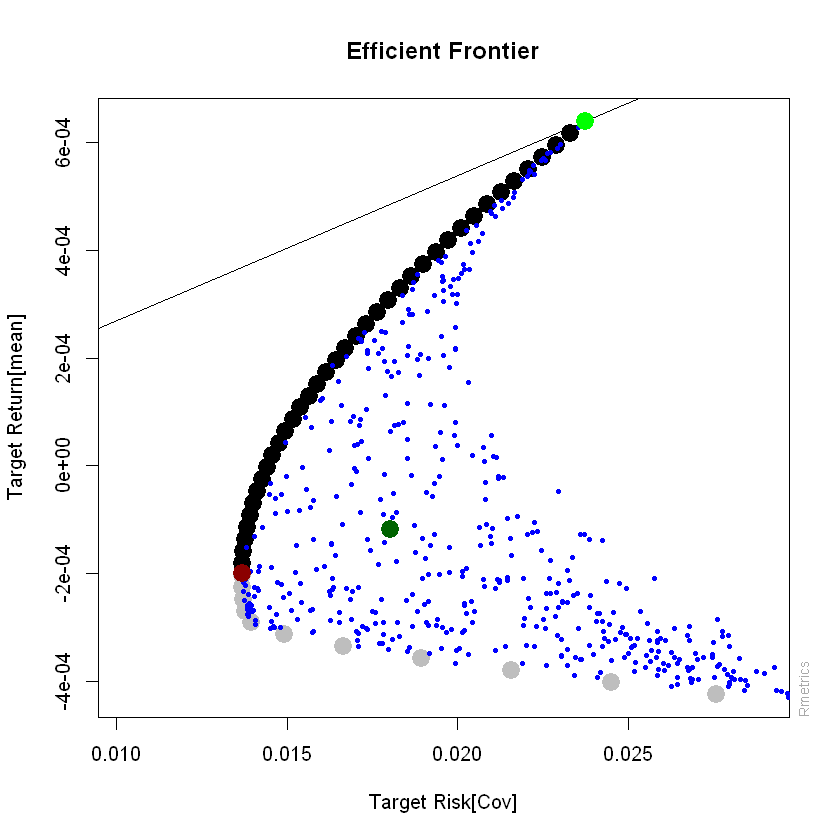
Conformación de un portafolio de inversión:#

plt.figure(figsize=(10, 6))
plt.scatter(volatility, returns_stocks, marker='o', color='darkgreen')
plt.grid()
plt.xlabel('Volatilidad')
plt.ylabel('Rendimiento')
plt.title('Rendimiento Vs. Volatilidad de PFBCOLOM, ISA y CEMARGOS')
for i in returns_stocks.index:
    plt.text(volatility[i], returns_stocks[i], i)
plt.show()

Vamos a conformar un portafolio de inversión con las tres acciones. Supondremos que asignamos pesos iguales a cada acción.

data.columns

Index(['CEMARGOS', 'ISA', 'PFBCOLOM'], dtype='object')

# Definir los pesos del portafolio (suma debe ser igual a 1)
weights = np.array([1/3, 1/3, 1/3])

# Calcular el rendimiento esperado del portafolio
portfolio_return = np.dot(returns_stocks, weights)

# Calcular la varianza del portafolio
portfolio_variance = np.dot(weights.T, np.dot(cov_matrix, weights))

# Calcular la volatilidad del portafolio (desviación estándar)
portfolio_volatility = np.sqrt(portfolio_variance)

print('Rendimiento esperado del portafolio:', portfolio_return)
print('Volatilidad del portafolio:', portfolio_volatility)

Rendimiento esperado del portafolio: 0.002517533985209985
Volatilidad del portafolio: 0.045137868344815806

# Graficar el portafolio
plt.figure(figsize=(10, 6))
plt.scatter(volatility, returns_stocks, marker='o', color='darkgreen')
plt.grid()
plt.xlabel('Volatilidad')
plt.ylabel('Rendimiento')
plt.title('Rendimiento Vs. Volatilidad de PFBCOLOM, ISA y CEMARGOS')
for i in returns_stocks.index:
    plt.text(volatility[i], returns_stocks[i], i)
plt.scatter(portfolio_volatility, portfolio_return, marker='x', color='red')
plt.text(portfolio_volatility, portfolio_return, 'Portafolio')
plt.show()

# Definir los pesos del portafolio (suma debe ser igual a 1)
weights = np.array([0.8, 0.1, 0.1])

# Calcular el rendimiento esperado del portafolio
portfolio_return = np.dot(returns_stocks, weights)

# Calcular la varianza del portafolio
portfolio_variance = np.dot(weights.T, np.dot(cov_matrix, weights))

# Calcular la volatilidad del portafolio (desviación estándar)
portfolio_volatility = np.sqrt(portfolio_variance)

print('Rendimiento esperado del portafolio:', portfolio_return)
print('Volatilidad del portafolio:', portfolio_volatility)

# Graficar el portafolio
plt.figure(figsize=(10, 6))
plt.scatter(volatility, returns_stocks, marker='o', color='darkgreen')
plt.grid()
plt.xlabel('Volatilidad')
plt.ylabel('Rendimiento')
plt.title('Rendimiento Vs. Volatilidad de PFBCOLOM, ISA y CEMARGOS')
for i in returns_stocks.index:
    plt.text(volatility[i], returns_stocks[i], i)
plt.scatter(portfolio_volatility, portfolio_return, marker='x', color='red')
plt.text(portfolio_volatility, portfolio_return, 'Portafolio')
plt.show()

Rendimiento esperado del portafolio: 0.0036374177636828335
Volatilidad del portafolio: 0.060469774368995755

# Definir los pesos del portafolio (suma debe ser igual a 1)
weights = np.array([0, 0.5, 0.5])

# Calcular el rendimiento esperado del portafolio
portfolio_return = np.dot(returns_stocks, weights)

# Calcular la varianza del portafolio
portfolio_variance = np.dot(weights.T, np.dot(cov_matrix, weights))

# Calcular la volatilidad del portafolio (desviación estándar)
portfolio_volatility = np.sqrt(portfolio_variance)

print('Rendimiento esperado del portafolio:', portfolio_return)
print('Volatilidad del portafolio:', portfolio_volatility)

# Graficar el portafolio
plt.figure(figsize=(10, 6))
plt.scatter(volatility, returns_stocks, marker='o', color='darkgreen')
plt.grid()
plt.xlabel('Volatilidad')
plt.ylabel('Rendimiento')
plt.title('Rendimiento Vs. Volatilidad de PFBCOLOM, ISA y CEMARGOS')
for i in returns_stocks.index:
    plt.text(volatility[i], returns_stocks[i], i)
plt.scatter(portfolio_volatility, portfolio_return, marker='x', color='red')
plt.text(portfolio_volatility, portfolio_return, 'Portafolio')
plt.show()

Rendimiento esperado del portafolio: 0.001717617000586522
Volatilidad del portafolio: 0.04273454569713671

Introducción a portafolios de inversión

Contents