Backtesting VaR Delta-Normal¶

Importar datos.¶

datos = read.csv("Tres acciones.csv", sep = ";")

Matriz de precios.¶

precios = datos[,-1]

Proporciones de inversión.¶

proporciones = c(0.25,0.5,0.25)

Matriz de rendimientos.¶

rendimientos = matrix(, nrow(precios)-1, ncol(precios))

for(i in 1:ncol(precios)){

  rendimientos[,i] = diff(log(precios[,i]))
}

Rendimientos portafolio de inversión¶

rendimientos_portafolio = vector()

for(i in 1:nrow(rendimientos)){

  rendimientos_portafolio[i] = sum(rendimientos[i,]*proporciones)
}

Ventana para Backtesting¶

Para realizar el Bakctesting se usa una ventana de los últimos rendimientos ventana_backtesting.

En este caso se utilizarán los últimos 250 rendimientos para realizar el Backtesting.

rendimientos_backtesting es una matriz con las filas igual a la ventana del Backtesting y con las columnas igual al número de acciones.

De los datos cargado se tienen 2815 rendimientos, sólo se usarán los últimos 250 que son desde el 2565 (2815-250) hasta el 2815.

En el siguiente código, los últimos 250 rendimientos se extraen de la siguiente manera: rendimientos[-c(nrow(rendimientos)-ventana_backtesting:nrow(rendimientos)),i]. Donde -c(nrow(rendimientos)-ventana_backtesting:nrow(rendimientos)) significa que se eliminarán los rendimientos más antiguos y sólo dejarán los últimos 250.

Lo mismo se realizará para los rendimientos del portafolio de inversión, se extraen los 250 rendimientos más recientes (rendimientos_backtesting_portafolio).

ventana_backtesting = 250

rendimientos_backtesting = matrix(, ventana_backtesting, ncol(rendimientos))

for(i in 1:ncol(rendimientos)){

rendimientos_backtesting[,i] = rendimientos[-c(nrow(rendimientos)-ventana_backtesting:nrow(rendimientos)), i]

}

#Para el portafolio de Inversión

rendimientos_backtesting_portafolio = rendimientos_portafolio[-c(nrow(rendimientos)-ventana_backtesting:nrow(rendimientos))]

Horizonte de tiempo de un día¶

t = 1

Backtesting método VaR Delta-Normal (NC = 95% y H = 250).¶

NC = 0.95

Para realizar un Backtesting con una ventana ($H$) de 250 rendimientos se debe calcular 250 VaR por cada uno de los métodos de VaR.

Para el método de VaR Delta-Normal se necesita la volatilidad histórica y el rendimiento medio en cada uno de los puntos en el tiempo de la ventana del Backtesting.

El siguiente código calcula la volatilidad histórica y el rendimiento medio iniciando en el rendimiento 2565 (2815-250) hata el 2815.

Volatilidad histórica y rendimiento medio (NC = 95% y H = 250)¶

volatilidad_historica = matrix(, ventana_backtesting, ncol(rendimientos))

rendimiento_medio = matrix(, ventana_backtesting, ncol(rendimientos))

for(j in 1:ncol(rendimientos)){

  for(i in 1:ventana_backtesting){

    volatilidad_historica[i,j] = sd(rendimientos[1:(nrow(rendimientos)-ventana_backtesting+i), j])

    rendimiento_medio[i,j] = mean(rendimientos[1:(nrow(rendimientos)-ventana_backtesting+i), j])
 }
}

Después de tener 250 volatilidades históricas y 250 rendimientos medios, se calcula 250 VaR por el método Delta-Normal sin promedios y con promedios.

VaR Delta-Normal para Backtesting (NC = 95% y H = 250)¶

VaR_sin_promedios = matrix(, ventana_backtesting, ncol(rendimientos))

VaR_con_promedios = matrix(, ventana_backtesting, ncol(rendimientos))

for(i in 1:ncol(rendimientos)){

    VaR_sin_promedios[,i] = volatilidad_historica[,i]*qnorm(NC)*sqrt(t)

    VaR_con_promedios[,i] = abs(qnorm(1-NC, mean = rendimiento_medio[,i]*t, sd=volatilidad_historica[,i]*sqrt(t)))
}

plot(rendimientos_backtesting[,1], t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "ECO")
lines(-VaR_sin_promedios[,1], t = "l",col = "darkred")
legend("topright","VaR sin promedios",lty = 1, col = "darkred")

plot(rendimientos_backtesting[,2], t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "PFBCOLOM")
lines(-VaR_sin_promedios[,2], t = "l", col = "darkred")
legend("topright","VaR sin promedios", lty = 1, col = "darkred")

plot(rendimientos_backtesting[,3], t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "ISA")
lines(-VaR_sin_promedios[,3], t = "l", col = "darkred")
legend("topright","VaR sin promedios", lty = 1, col = "darkred")

plot(rendimientos_backtesting[,1], t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "ECO")
lines(-VaR_con_promedios[,1], t = "l", col = "darkred")
legend("topright","VaR con promedios", lty = 1, col = "darkred")

plot(rendimientos_backtesting[,2], t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "PFBCOLOM")
lines(-VaR_con_promedios[,2], t = "l", col = "darkred")
legend("topright","VaR con promedios", lty = 1, col = "darkred")

plot(rendimientos_backtesting[,3], t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "ISA")
lines(-VaR_con_promedios[,3], t = "l", col = "darkred")
legend("topright","VaR con promedios", lty = 1, col = "darkred")

Excepciones VaR Delta-Normal (NC = 95% y H = 250)¶

Existe una excepción cuando la pérdida del día es mayor que el VaR. En otras palabras, se compara cada uno de los VaR hallados anteriormente con los rendimientos del mismo período de tiempo y si el rendimiento negativo es menor (más negativo) que VaR negativo, entonces se cuenta como una exepción. Luego se calculan las proporciones de excepción $𝑝 ̂ $:

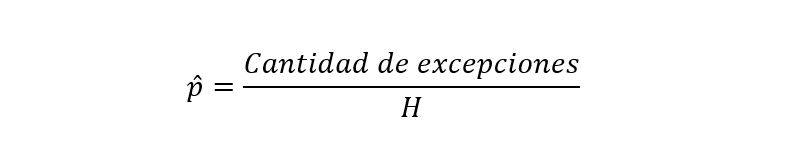
1¶

Cantidad de excepciones: Cantidad de pérdidas mayores al VaR.

H: Cantidad de observaciones diarias utilizadas para realizar el backtesting ventana_backtesting.

excepciones_sin_promedios = vector()

excepciones_con_promedios = vector()

for(i in 1:ncol(rendimientos)){

 excepciones_sin_promedios[i] = sum(ifelse(-VaR_sin_promedios[,i] > rendimientos_backtesting[,i], 1, 0))

 excepciones_con_promedios[i] = sum(ifelse(-VaR_con_promedios[,i] > rendimientos_backtesting[,i], 1, 0))

}

p.gorro_sin_promedios = excepciones_sin_promedios/ventana_backtesting

p.gorro_con_promedios = excepciones_con_promedios/ventana_backtesting

excepciones_sin_promedios
excepciones_con_promedios
p.gorro_sin_promedios
p.gorro_con_promedios

17
6
15

17
7
16

0.068
0.024
0.06

0.068
0.028
0.064

En el método VaR Delta-Normal sin promedios se hallaron 17 exepciones en la acción de ECO, 6 en PFBCOLOM y 15 en ISA. Que corresponde a un 6,8%, 2,4% y 6%, respectivamente.

En el método VaR Delta-Normal con promedios se hallaron 17 exepciones en la acción de ECO, 7 en PFBCOLOM y 16 en ISA. Que corresponde a un 6,8%, 2,8% y 6,4%, respectivamente.

Como el nivel de confianza es del 95%, se espera una proporción de exepción aproximada al 5% en cada de las acciones.

Con las proporciones de exepción mayores al 5%, aparentemente el VaR está subvalornado el riesgo porque el método de VaR implementado está cubriendo más porcentaje de las pérdidas cuanto está diseñado para un cubrimiento del 5% (α).

Con las proporciones de exepción menores al 5%, aparentemente el VaR está subrevalornado el riesgo porque el método de VaR implementado está cubriendo menos porcentaje de las pérdidas cuanto está diseñado para un cubrimiento del 5% (α).

Sin embargo, se aconseja otros métodos de Backtesting para determinar si el VaR empleado es adecuado. El siguiente método de Backtesting tiene como insumo las proporciones de exepción $𝑝 ̂ $.

Prueba de Kupiec VaR Delta-Normal (NC = 95% y H = 250)¶

Esta prueba determina lo lejos que se encuentra la proporción de exepción estimada de la cobertura deseada (α).

Evalúa la hipótesis nula de que $𝑝 ̂ =\alpha$

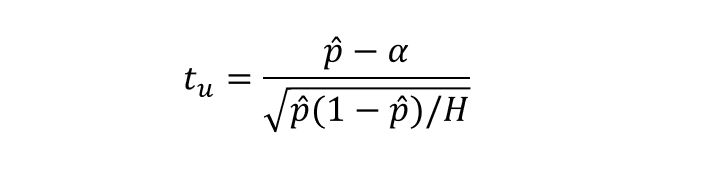
2¶

$𝑡_𝑢:$ Estadístico de Kupiec.

$𝑝 ̂:$ Proporción de excepciones.

𝛼: Significancia del VaR (1 – N.C.).

H: Cantidad de observaciones diarias utilizadas para realizar el backtesting.

tu_sin_promedios = (p.gorro_sin_promedios-(1-NC))/sqrt(p.gorro_sin_promedios*(1-p.gorro_sin_promedios)/ventana_backtesting)

tu_con_promedios = (p.gorro_con_promedios-(1-NC))/sqrt(p.gorro_con_promedios*(1-p.gorro_con_promedios)/ventana_backtesting)

tu_critico = abs(qt((1-NC)/2, ventana_backtesting-1))

tu_sin_promedios
tu_con_promedios
tu_critico

1.1305248081457
-2.68604214493585
0.665779551614131

1.1305248081457
-2.10853365354609
0.904419939712976

1.96953686764035

La hipótesis nula se rechaza si el valor absoluto de $𝑡_𝑢$ es mayor que el valor absoluto del $t$ crítico de la distribución $t$ con $H – 1$ grados de libertad.

Kupiec demostró que el estadístico $𝑡_𝑢$ sigue una distribución $t$ con $H – 1$ grados de libertad.

Si el valor absoluto de :math:`𝑡_𝑢` es mayor que el valor absoluto del :math:`t` crítico: Se rechaza el modelo de VaR empleado.

\[|𝑡_𝑢| > |t_{crítico}|\]

En el ejemplo anterior el $t$ crítico es de $1.96953686764035$. Ahora se evaluará cada uno de los $𝑡_𝑢$ y se determinará para cada acción si los dos métodos de VaR empleados son aprobados o no.

De acuerdo con el siguiente código, una salida de $1$ significa que el método de VaR se aprueba en cada acción y $0$ que se rechaza.

aprobados_sin_promedios = vector()

aprobados_con_promedios = vector()

for(i in 1:ncol(rendimientos)){

    aprobados_sin_promedios[i] = ifelse(abs(tu_sin_promedios[i]) < tu_critico,aprobados_sin_promedios[i] <- 1, aprobados_sin_promedios[i] <- 0)

    aprobados_con_promedios[i] = ifelse(abs(tu_con_promedios[i]) < tu_critico,aprobados_con_promedios[i] <- 1,aprobados_con_promedios[i] <- 0)
  }

aprobados_sin_promedios

aprobados_con_promedios

1
0
1

1
0
1

Los $1$ significan que el método de VaR se acepta y los $0$ que se rechaza por el método de Kupiec.

Los métodos de VaR Delta-Normal sin promedios y con promedios se aceptan para las acciones de ECO e ISA. En cambio, en la acción de PFBCOLOM los dos métodos de VaR se rechazan, no son adecuados para medir el riesgo para esta acción.

Para el portafolio de inversión se debe calcular la volatilidad histórica y el rendimiento medio a partir de los rendimientos del portafolio de inversión y para la ventana Backtesting.

Volatilidad y rendimiento medio del portafolio (NC = 95% y H = 250)¶

volatilidad_historica_portafolio = vector()

rendimiento_medio_portafolio = vector()

for(i in 1:ventana_backtesting){

    volatilidad_historica_portafolio[i] = sd(rendimientos_portafolio[1:(nrow(rendimientos)-ventana_backtesting+i)])

    rendimiento_medio_portafolio[i] = mean(rendimientos_portafolio[1:(nrow(rendimientos)-ventana_backtesting+i)])
}

VaR Delta-Normal del portafolio de inversión para Backtesting (NC = 95% y H = 250)¶

VaR_portafolio_sin_promedios = vector()

VaR_portafolio_con_promedios = vector()

for(i in 1:ventana_backtesting){

    VaR_portafolio_sin_promedios[i] = volatilidad_historica_portafolio[i]*qnorm(NC)*sqrt(t)

    VaR_portafolio_con_promedios[i]  =abs(qnorm(1-NC, mean = rendimiento_medio_portafolio[i], sd = volatilidad_historica_portafolio[i]))

}

plot(rendimientos_backtesting_portafolio, t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "Portafolio de inversión")
lines(-VaR_portafolio_sin_promedios, t = "l", col = "darkred")
legend("topright","VaR sin promedios", lty = 1, col = "darkred")

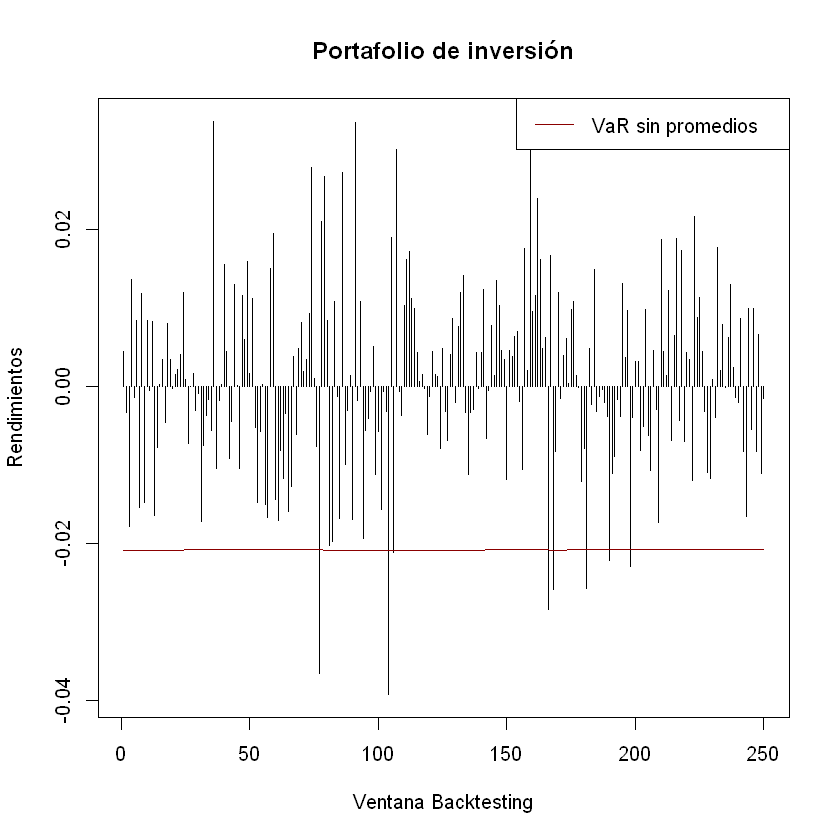
plot(rendimientos_backtesting_portafolio, t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "Portafolio de inversión")
lines(-VaR_portafolio_con_promedios, t = "l", col = "darkred")
legend("topright","VaR con promedios", lty = 1, col = "darkred")

Excepciones VaR Delta-Normal del portafolio de inversión (NC = 95% y H = 250)¶

excepciones_sin_promedios_portafolio = sum(ifelse(-VaR_portafolio_sin_promedios > rendimientos_backtesting_portafolio, 1, 0))

excepciones_con_promedios_portafolio = sum(ifelse(-VaR_portafolio_con_promedios > rendimientos_backtesting_portafolio, 1, 0))

p.gorro_sin_promedios_portafolio = excepciones_sin_promedios_portafolio/ventana_backtesting

p.gorro_con_promedios_portafolio = excepciones_con_promedios_portafolio/ventana_backtesting

excepciones_sin_promedios_portafolio

excepciones_con_promedios_portafolio

p.gorro_sin_promedios_portafolio

p.gorro_con_promedios_portafolio

880.0320.032

Prueba de Kupiec VaR Delta-Normal del portafolio de inversión (NC = 95% y H = 250)¶

tu_sin_promedios_portafolio = (p.gorro_sin_promedios_portafolio-(1-NC))/sqrt(p.gorro_sin_promedios_portafolio*(1-p.gorro_sin_promedios_portafolio)/ventana_backtesting)

tu_con_promedios_portafolio = (p.gorro_con_promedios_portafolio-(1-NC))/sqrt(p.gorro_con_promedios_portafolio*(1-p.gorro_con_promedios_portafolio)/ventana_backtesting)

tu_critico = abs(qt((1-NC)/2, ventana_backtesting-1))

aprobados_sin_promedios_portafolio = ifelse(abs(tu_sin_promedios_portafolio) < tu_critico, aprobados_sin_promedios_portafolio <- 1, aprobados_sin_promedios_portafolio <- 0)

aprobados_con_promedios_portafolio = ifelse(abs(tu_con_promedios_portafolio) < tu_critico, aprobados_con_promedios_portafolio <- 1, aprobados_con_promedios_portafolio <- 0)

aprobados_sin_promedios_portafolio

aprobados_con_promedios_portafolio

11

Conclusión:¶

Con con una ventana de 250 y nivel de confianza del 95%, los métodos de VaR Delta-Normal sin promedios y con promedios son aceptados para las acciones de ECO e ISA y para el portafolio de inversión; sin embargo, en la acción de PFBCOLOM no se aceptaron los dos métodos de VaR. Se debe cambiar la ventana Backtesting o el nivel de confianza para determinar de qué forma el método de VaR es adecuado.

Para esto solo se cambiará el nivel de confianza a 99% y se volverá a realizar el procedimiento de Backtesting anterior desde VaR Delta-Normal con ventana Backtesting.

Si se hubiera cambiado la ventana Backtesting se debería empezar desde el principio del Backtesting (Ventana para Backtesting).

Backtesting método VaR Delta-Normal (NC = 99% y H = 250)¶

NC = 0.99

VaR Delta-Normal para Backtesting (NC = 99% y H = 250)¶

VaR_sin_promedios = matrix(, ventana_backtesting, ncol(rendimientos))

VaR_con_promedios = matrix(, ventana_backtesting, ncol(rendimientos))

for(i in 1:ncol(rendimientos)){

    VaR_sin_promedios[,i] = volatilidad_historica[,i]*qnorm(NC)*sqrt(t)

    VaR_con_promedios[,i] = abs(qnorm(1-NC, mean = rendimiento_medio[,i]*t, sd = volatilidad_historica[,i]*sqrt(t)))
}

plot(rendimientos_backtesting[,1], t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "ECO")
lines(-VaR_sin_promedios[,1], t = "l", col = "darkred")
legend("topright","VaR sin promedios", lty = 1, col = "darkred")

plot(rendimientos_backtesting[,2], t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "PFBCOLOM")
lines(-VaR_sin_promedios[,2], t = "l", col = "darkred")
legend("topright","VaR sin promedios", lty = 1, col = "darkred")

plot(rendimientos_backtesting[,3], t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "ISA")
lines(-VaR_sin_promedios[,3], t = "l", col = "darkred")
legend("topright","VaR sin promedios", lty = 1, col = "darkred")

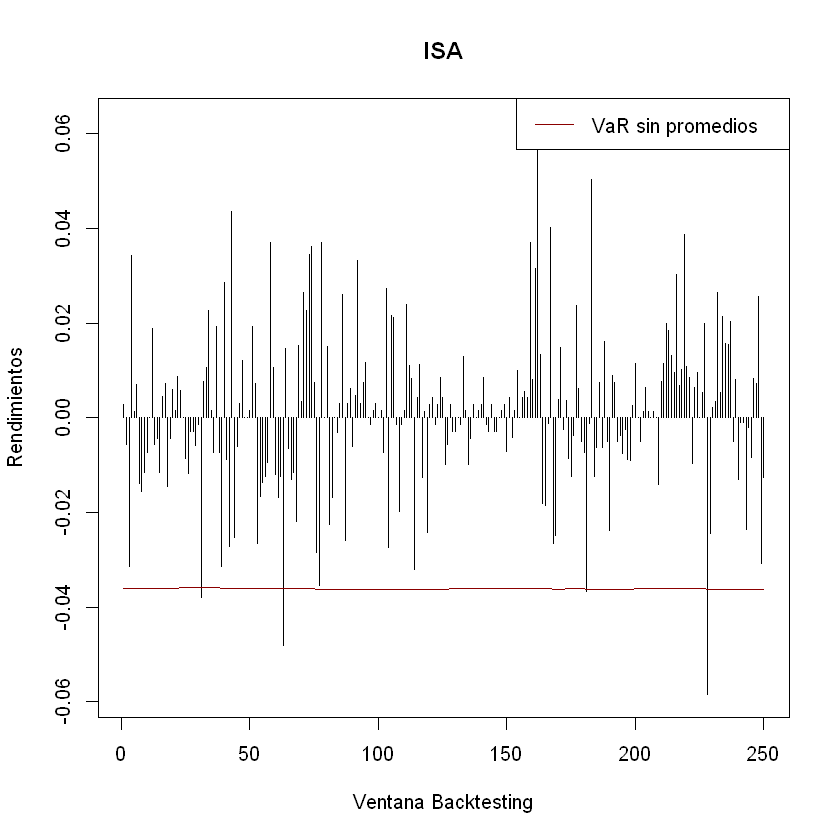
plot(rendimientos_backtesting[,1], t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "ECO")
lines(-VaR_sin_promedios[,1], t = "l", col = "darkred")
legend("topright","VaR con promedios", lty = 1, col = "darkred")

plot(rendimientos_backtesting[,2], t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "PFBCOLOM")
lines(-VaR_sin_promedios[,2], t = "l", col = "darkred")
legend("topright","VaR con promedios", lty = 1, col = "darkred")

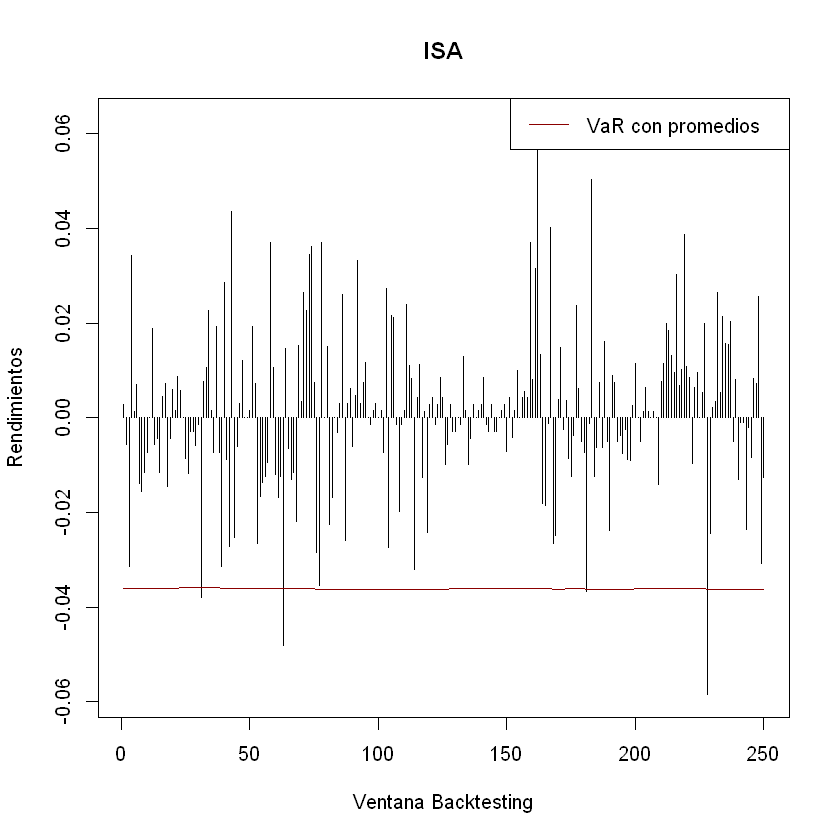
plot(rendimientos_backtesting[,3], t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "ISA")
lines(-VaR_sin_promedios[,3], t = "l", col = "darkred")
legend("topright","VaR con promedios", lty = 1, col = "darkred")

Excepciones VaR Delta-Normal (NC = 99% y H = 250)¶

excepciones_sin_promedios = vector()

excepciones_con_promedios = vector()

for(i in 1:ncol(rendimientos)){

 excepciones_sin_promedios[i] = sum(ifelse(-VaR_sin_promedios[,i] > rendimientos_backtesting[,i], 1, 0))

 excepciones_con_promedios[i] = sum(ifelse(-VaR_con_promedios[,i] > rendimientos_backtesting[,i], 1, 0))

}

p.gorro_sin_promedios = excepciones_sin_promedios/ventana_backtesting

p.gorro_con_promedios = excepciones_con_promedios/ventana_backtesting

excepciones_sin_promedios

excepciones_con_promedios

p.gorro_sin_promedios

p.gorro_con_promedios

7
0
4

7
1
4

0.028
0
0.016

0.028
0.004
0.016

Prueba de Kupiec VaR Delta-Normal (NC = 99% y H = 250)¶

tu_sin_promedios = (p.gorro_sin_promedios-(1-NC))/sqrt(p.gorro_sin_promedios*(1-p.gorro_sin_promedios)/ventana_backtesting)

tu_con_promedios = (p.gorro_con_promedios-(1-NC))/sqrt(p.gorro_con_promedios*(1-p.gorro_con_promedios)/ventana_backtesting)

tu_critico = abs(qt((1-NC)/2, ventana_backtesting-1))

tu_sin_promedios

tu_con_promedios

tu_critico

1.72516389835588
-Inf
0.756072973636416

1.72516389835588
-1.50300903010538
0.756072973636416

2.59571775827349

aprobados_sin_promedios = vector()

aprobados_con_promedios = vector()

for(i in 1:ncol(rendimientos)){

    aprobados_sin_promedios[i] = ifelse(abs(tu_sin_promedios[i]) < tu_critico, aprobados_sin_promedios[i] <- 1, aprobados_sin_promedios[i] <- 0)

    aprobados_con_promedios[i] = ifelse(abs(tu_con_promedios[i]) < tu_critico, aprobados_con_promedios[i] <- 1, aprobados_con_promedios[i] <- 0)
  }

aprobados_sin_promedios

aprobados_con_promedios

1
0
1

1
1
1

Con una ventana Backtesting de 250 rendimientos y nivel de confianza del 99%, el método VaR con promedios es aceptado para las tres acciones. El método VaR sin promedio sigue rechazado en la acción PFBCOLOM.

VaR Delta-Normal para Backtesting del portafolio de inversión (NC = 99% y H = 250)¶

VaR_portafolio_sin_promedios = vector()

VaR_portafolio_con_promedios = vector()

for(i in 1:ventana_backtesting){

    VaR_portafolio_sin_promedios[i] = volatilidad_historica_portafolio[i]*qnorm(NC)*sqrt(t)

    VaR_portafolio_con_promedios[i] = abs(qnorm(1-NC, mean = rendimiento_medio_portafolio[i], sd = volatilidad_historica_portafolio[i]))

}

plot(rendimientos_backtesting_portafolio, t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "Portafolio de inversión")
lines(-VaR_portafolio_sin_promedios, t = "l", col = "darkred")
legend("topright","VaR sin promedios", lty = 1, col = "darkred")

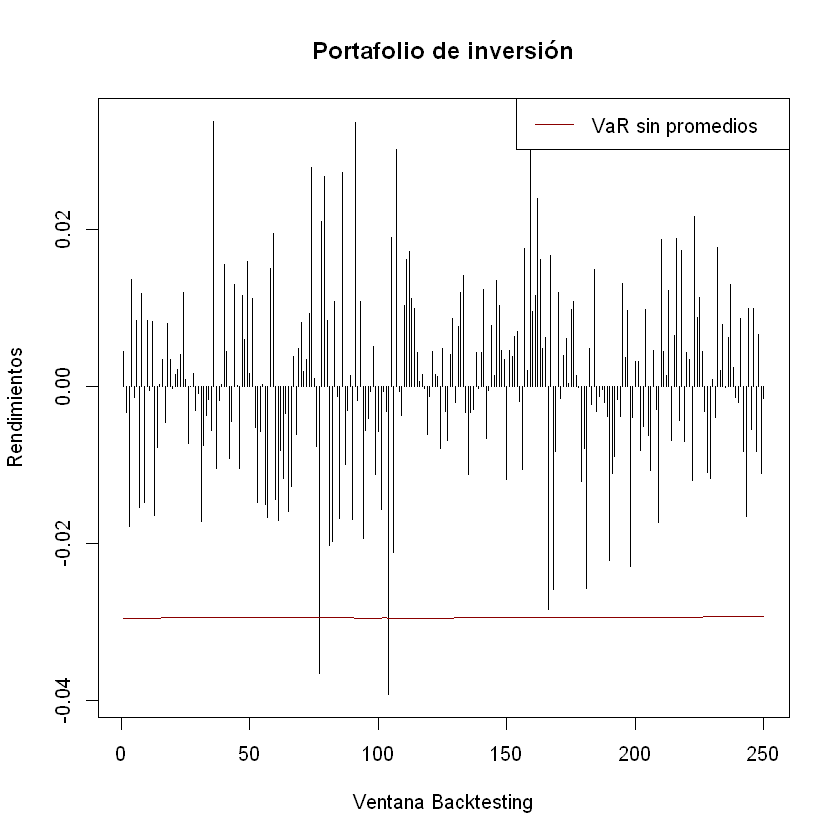
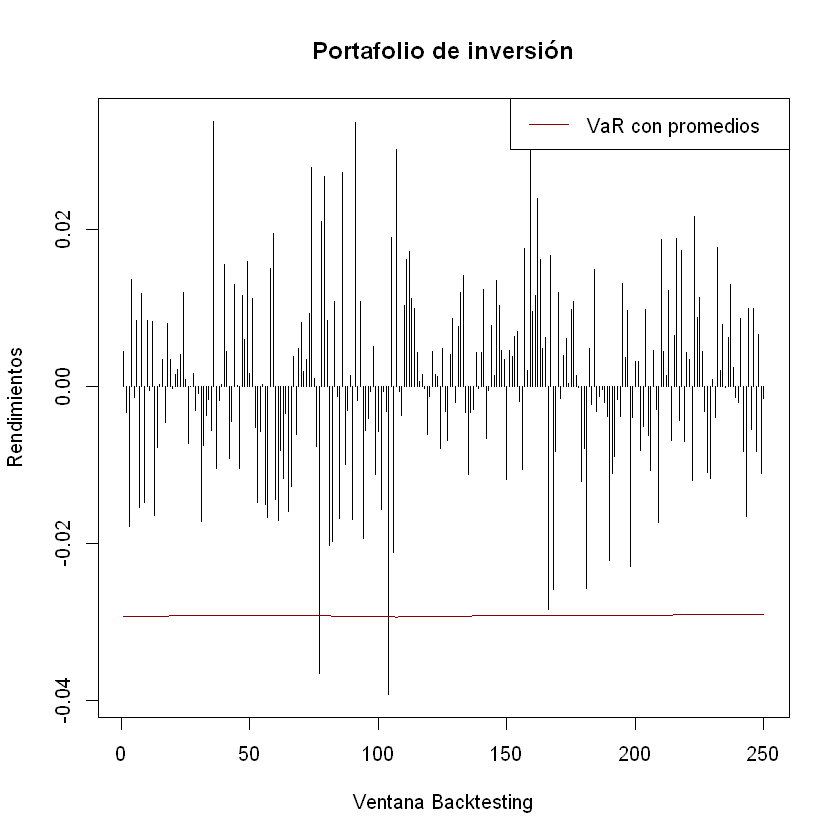
plot(rendimientos_backtesting_portafolio, t = "h", xlab = "Ventana Backtesting", ylab = "Rendimientos", main = "Portafolio de inversión")
lines(-VaR_portafolio_con_promedios, t = "l", col = "darkred")
legend("topright","VaR con promedios", lty = 1, col = "darkred")

Excepciones VaR Delta-Normal del portafolio de inversión (NC = 99% y H = 250)¶

excepciones_sin_promedios_portafolio = sum(ifelse(-VaR_portafolio_sin_promedios > rendimientos_backtesting_portafolio, 1, 0))

excepciones_con_promedios_portafolio = sum(ifelse(-VaR_portafolio_con_promedios > rendimientos_backtesting_portafolio, 1, 0))

p.gorro_sin_promedios_portafolio = excepciones_sin_promedios_portafolio/ventana_backtesting

p.gorro_con_promedios_portafolio = excepciones_con_promedios_portafolio/ventana_backtesting

excepciones_sin_promedios_portafolio

excepciones_con_promedios_portafolio

p.gorro_sin_promedios_portafolio

p.gorro_con_promedios_portafolio

220.0080.008

Prueba de Kupiec VaR Delta-Normal (NC = 99% y H = 250)¶

tu_sin_promedios_portafolio = (p.gorro_sin_promedios_portafolio-(1-NC))/sqrt(p.gorro_sin_promedios_portafolio*(1-p.gorro_sin_promedios_portafolio)/ventana_backtesting)

tu_con_promedios_portafolio = (p.gorro_con_promedios_portafolio-(1-NC))/sqrt(p.gorro_con_promedios_portafolio*(1-p.gorro_con_promedios_portafolio)/ventana_backtesting)

tu_critico = abs(qt((1-NC)/2, ventana_backtesting-1))

aprobados_sin_promedios_portafolio = ifelse(abs(tu_sin_promedios_portafolio) < tu_critico,aprobados_sin_promedios_portafolio <- 1, aprobados_sin_promedios_portafolio <- 0)

aprobados_con_promedios_portafolio = ifelse(abs(tu_con_promedios_portafolio) < tu_critico,aprobados_con_promedios_portafolio <- 1, aprobados_con_promedios_portafolio <- 0)

aprobados_sin_promedios_portafolio

aprobados_con_promedios_portafolio

11

Conclusión:¶

Con con una ventana de 250 y nivel de confianza del 99%, los métodos de VaR Delta-Normal sin promedios y con promedios son aceptados para las acciones de ECO e ISA y para el portafolio de inversión. En la acción PFBCOLOM sólo se aceptó el método con promedios.

Backtesting método VaR Delta-Normal (NC = 99% y H = 500)¶

Se realizará el Backtesting con una ventana de 500 y nivel de confianza del 99%.

NC = 0.99

Ventana para Backtesting¶

ventana_backtesting = 500

rendimientos_backtesting = matrix(, ventana_backtesting, ncol(rendimientos))

for(i in 1:ncol(rendimientos)){

rendimientos_backtesting[,i] = rendimientos[-c(nrow(rendimientos)-ventana_backtesting:nrow(rendimientos)), i]
}

#Para el portafolio de Inversión

rendimientos_backtesting_portafolio = rendimientos_portafolio[-c(nrow(rendimientos)-ventana_backtesting:nrow(rendimientos))]

Volatilidad histórica y rendimiento medio (NC = 99% y H = 500)¶

volatilidad_historica = matrix(, ventana_backtesting, ncol(rendimientos))

rendimiento_medio = matrix(, ventana_backtesting, ncol(rendimientos))

for(j in 1:ncol(rendimientos)){

  for(i in 1:ventana_backtesting){

    volatilidad_historica[i,j] = sd(rendimientos[1:(nrow(rendimientos)-ventana_backtesting+i), j])

    rendimiento_medio[i,j] = mean(rendimientos[1:(nrow(rendimientos)-ventana_backtesting+i), j])
 }
}

Después de tener 500 volatilidades históricas y 500 rendimientos medios, se calcula 500 VaR por el método Delta-Normal sin promedios y con promedios.

VaR Delta-Normal para Backtesting (NC = 99% y H = 500)¶

VaR_sin_promedios = matrix(, ventana_backtesting, ncol(rendimientos))

VaR_con_promedios = matrix(, ventana_backtesting, ncol(rendimientos))

for(i in 1:ncol(rendimientos)){

    VaR_sin_promedios[,i] = volatilidad_historica[,i]*qnorm(NC)*sqrt(t)

    VaR_con_promedios[,i] = abs(qnorm(1-NC, mean = rendimiento_medio[,i]*t, sd = volatilidad_historica[,i]*sqrt(t)))
}

Excepciones VaR Delta-Normal (NC = 99% y H = 500)¶

excepciones_sin_promedios = vector()

excepciones_con_promedios = vector()

for(i in 1:ncol(rendimientos)){

 excepciones_sin_promedios[i] = sum(ifelse(-VaR_sin_promedios[,i] > rendimientos_backtesting[,i], 1, 0))

 excepciones_con_promedios[i] = sum(ifelse(-VaR_con_promedios[,i] > rendimientos_backtesting[,i], 1, 0))

}

p.gorro_sin_promedios = excepciones_sin_promedios/ventana_backtesting

p.gorro_con_promedios = excepciones_con_promedios/ventana_backtesting

excepciones_sin_promedios

excepciones_con_promedios

p.gorro_sin_promedios

p.gorro_con_promedios

12
2
6

12
3
6

0.024
0.004
0.012

0.024
0.006
0.012

Prueba de Kupiec VaR Delta-Normal (NC = 99% y H = 500)¶

tu_sin_promedios = (p.gorro_sin_promedios-(1-NC))/sqrt(p.gorro_sin_promedios*(1-p.gorro_sin_promedios)/ventana_backtesting)

tu_con_promedios = (p.gorro_con_promedios-(1-NC))/sqrt(p.gorro_con_promedios*(1-p.gorro_con_promedios)/ventana_backtesting)

tu_critico = abs(qt((1-NC)/2, ventana_backtesting-1))

tu_sin_promedios

tu_con_promedios

tu_critico

2.04542004717831
-2.12557575474426
0.410720048408452

2.04542004717831
-1.15818030680537
0.410720048408452

2.58571768311175

aprobados_sin_promedios = vector()

aprobados_con_promedios = vector()

for(i in 1:ncol(rendimientos)){

    aprobados_sin_promedios[i] = ifelse(abs(tu_sin_promedios[i]) < tu_critico, aprobados_sin_promedios[i] <- 1, aprobados_sin_promedios[i] <- 0)

    aprobados_con_promedios[i] = ifelse(abs(tu_con_promedios[i]) < tu_critico,aprobados_con_promedios[i] <- 1, aprobados_con_promedios[i] <- 0)
  }

aprobados_sin_promedios

aprobados_con_promedios

1
1
1

1
1
1

Con una ventana Backtesting de 500 rendimientos y nivel de confianza del 99%, los métodos de VaR Delta-Normal sin promedios y con promedios son aceptados para las tres acciones.

Volatilidad y rendimiento medio del portafolio (NC = 99% y H = 500)¶

volatilidad_historica_portafolio = vector()

rendimiento_medio_portafolio = vector()

for(i in 1:ventana_backtesting){

    volatilidad_historica_portafolio[i] = sd(rendimientos_portafolio[1:(nrow(rendimientos)-ventana_backtesting+i)])

    rendimiento_medio_portafolio[i] = mean(rendimientos_portafolio[1:(nrow(rendimientos)-ventana_backtesting+i)])
}

VaR Delta-Normal para Backtesting del portafolio de inversión (NC = 99% y H = 500)¶

VaR_portafolio_sin_promedios = vector()

VaR_portafolio_con_promedios = vector()

for(i in 1:ventana_backtesting){

    VaR_portafolio_sin_promedios[i] = volatilidad_historica_portafolio[i]*qnorm(NC)*sqrt(t)

    VaR_portafolio_con_promedios[i] = abs(qnorm(1-NC, mean = rendimiento_medio_portafolio[i], sd = volatilidad_historica_portafolio[i]))

}

Excepciones VaR Delta-Normal del portafolio de inversión (NC = 99% y H = 500)¶

excepciones_sin_promedios_portafolio = sum(ifelse(-VaR_portafolio_sin_promedios > rendimientos_backtesting_portafolio, 1, 0))

excepciones_con_promedios_portafolio = sum(ifelse(-VaR_portafolio_con_promedios > rendimientos_backtesting_portafolio, 1, 0))

p.gorro_sin_promedios_portafolio = excepciones_sin_promedios_portafolio/ventana_backtesting

p.gorro_con_promedios_portafolio = excepciones_con_promedios_portafolio/ventana_backtesting

excepciones_sin_promedios_portafolio

excepciones_con_promedios_portafolio

p.gorro_sin_promedios_portafolio

p.gorro_con_promedios_portafolio

550.010.01

Prueba de Kupiec VaR Delta-Normal (NC = 99% y H = 500)¶

tu_sin_promedios_portafolio = (p.gorro_sin_promedios_portafolio-(1-NC))/sqrt(p.gorro_sin_promedios_portafolio*(1-p.gorro_sin_promedios_portafolio)/ventana_backtesting)

tu_con_promedios_portafolio = (p.gorro_con_promedios_portafolio-(1-NC))/sqrt(p.gorro_con_promedios_portafolio*(1-p.gorro_con_promedios_portafolio)/ventana_backtesting)

tu_critico = abs(qt((1-NC)/2 ,ventana_backtesting-1))

aprobados_sin_promedios_portafolio = ifelse(abs(tu_sin_promedios_portafolio) < tu_critico,aprobados_sin_promedios_portafolio <- 1, aprobados_sin_promedios_portafolio <- 0)

aprobados_con_promedios_portafolio = ifelse(abs(tu_con_promedios_portafolio) < tu_critico,aprobados_con_promedios_portafolio <- 1, aprobados_con_promedios_portafolio <- 0)

aprobados_sin_promedios_portafolio

aprobados_con_promedios_portafolio

11

Conclusión:¶

Con con una ventana de 500 y nivel de confianza del 99%, los métodos de VaR Delta-Normal sin promedios y con promedios son aceptados para las tres acciones y el portafolio de inversión.

Backtesting método VaR Delta-Normal (NC = 95% y H = 500)¶

Se realizará el Backtesting con una ventana de 500 y nivel de confianza del 95%.

NC = 0.95

VaR Delta-Normal para Backtesting (NC = 95% y H = 500)¶

VaR_sin_promedios = matrix(, ventana_backtesting, ncol(rendimientos))

VaR_con_promedios = matrix(, ventana_backtesting, ncol(rendimientos))

for(i in 1:ncol(rendimientos)){

    VaR_sin_promedios[,i] = volatilidad_historica[,i]*qnorm(NC)*sqrt(t)

    VaR_con_promedios[,i] = abs(qnorm(1-NC, mean = rendimiento_medio[,i]*t, sd = volatilidad_historica[,i]*sqrt(t)))
}

Excepciones VaR Delta-Normal (NC = 95% y H = 500)¶

excepciones_sin_promedios = vector()

excepciones_con_promedios = vector()

for(i in 1:ncol(rendimientos)){

 excepciones_sin_promedios[i] = sum(ifelse(-VaR_sin_promedios[,i] > rendimientos_backtesting[,i], 1, 0))

 excepciones_con_promedios[i] = sum(ifelse(-VaR_con_promedios[,i] > rendimientos_backtesting[,i], 1, 0))

}

p.gorro_sin_promedios = excepciones_sin_promedios/ventana_backtesting

p.gorro_con_promedios = excepciones_con_promedios/ventana_backtesting

excepciones_sin_promedios

excepciones_con_promedios

p.gorro_sin_promedios

p.gorro_con_promedios

28
12
22

28
13
23

0.056
0.024
0.044

0.056
0.026
0.046

Prueba de Kupiec VaR Delta-Normal (NC = 95% y H = 500)¶

tu_sin_promedios = (p.gorro_sin_promedios-(1-NC))/sqrt(p.gorro_sin_promedios*(1-p.gorro_sin_promedios)/ventana_backtesting)

tu_con_promedios = (p.gorro_con_promedios-(1-NC))/sqrt(p.gorro_con_promedios*(1-p.gorro_con_promedios)/ventana_backtesting)

tu_critico = abs(qt((1-NC)/2, ventana_backtesting-1))

tu_sin_promedios

tu_con_promedios

tu_critico

0.583520666333881
-3.798637230474
-0.654155456274547

0.583520666333881
-3.37233019764278
-0.426964621149184

1.96472939098769

aprobados_sin_promedios = vector()

aprobados_con_promedios = vector()

for(i in 1:ncol(rendimientos)){

    aprobados_sin_promedios[i] = ifelse(abs(tu_sin_promedios[i]) < tu_critico, aprobados_sin_promedios[i] <- 1, aprobados_sin_promedios[i] <- 0)

    aprobados_con_promedios[i] = ifelse(abs(tu_con_promedios[i]) < tu_critico, aprobados_con_promedios[i] <- 1, aprobados_con_promedios[i] <- 0)
  }

aprobados_sin_promedios

aprobados_con_promedios

1
0
1

1
0
1

Con una ventana Backtesting de 500 rendimientos y nivel de confianza del 95%, los métodos de VaR Delta-Normal sin promedios y con promedios son aceptados para las tres acciones.

VaR Delta-Normal para Backtesting del portafolio de inversión (NC = 95% y H = 500)¶

VaR_portafolio_sin_promedios = vector()

VaR_portafolio_con_promedios = vector()

for(i in 1:ventana_backtesting){

    VaR_portafolio_sin_promedios[i] = volatilidad_historica_portafolio[i]*qnorm(NC)*sqrt(t)

    VaR_portafolio_con_promedios[i] = abs(qnorm(1-NC, mean = rendimiento_medio_portafolio[i], sd = volatilidad_historica_portafolio[i]))

}

Excepciones VaR Delta-Normal del portafolio de inversión (NC = 95% y H = 500)¶

excepciones_sin_promedios_portafolio = sum(ifelse(-VaR_portafolio_sin_promedios > rendimientos_backtesting_portafolio, 1, 0))

excepciones_con_promedios_portafolio = sum(ifelse(-VaR_portafolio_con_promedios > rendimientos_backtesting_portafolio, 1, 0))

p.gorro_sin_promedios_portafolio = excepciones_sin_promedios_portafolio/ventana_backtesting

p.gorro_con_promedios_portafolio = excepciones_con_promedios_portafolio/ventana_backtesting

excepciones_sin_promedios_portafolio

excepciones_con_promedios_portafolio

p.gorro_sin_promedios_portafolio

p.gorro_con_promedios_portafolio

15150.030.03

Prueba de Kupiec VaR Delta-Normal (NC = 95% y H = 500)¶

tu_sin_promedios_portafolio = (p.gorro_sin_promedios_portafolio-(1-NC))/sqrt(p.gorro_sin_promedios_portafolio*(1-p.gorro_sin_promedios_portafolio)/ventana_backtesting)

tu_con_promedios_portafolio = (p.gorro_con_promedios_portafolio-(1-NC))/sqrt(p.gorro_con_promedios_portafolio*(1-p.gorro_con_promedios_portafolio)/ventana_backtesting)

tu_critico = abs(qt((1-NC)/2, ventana_backtesting-1))

aprobados_sin_promedios_portafolio = ifelse(abs(tu_sin_promedios_portafolio) < tu_critico, aprobados_sin_promedios_portafolio <- 1, aprobados_sin_promedios_portafolio <- 0)

aprobados_con_promedios_portafolio = ifelse(abs(tu_con_promedios_portafolio) < tu_critico, aprobados_con_promedios_portafolio <- 1, aprobados_con_promedios_portafolio <- 0)

aprobados_sin_promedios_portafolio

aprobados_con_promedios_portafolio

00

Conclusión:¶

Con con una ventana de 500 y nivel de confianza del 95%, los métodos de VaR Delta-Normal sin promedios y con promedios son aceptados para las tres acciones y el portafolio de inversión.

Conclusión general:¶

	ECO	PFBCOLOMB	ISA	Portafolio*
VaR sin promedios, NC = 95% y H = 250	Aceptado	Rechazado	Aceptado	Aceptado
VaR con promedios, NC = 95% y H = 250	Aceptado	Rechazado	Aceptado	Aceptado
VaR sin promedios, NC = 95% y H = 500	Aceptado	Rechazado	Aceptado	Rechazado
VaR con promedios, NC = 95% y H = 500	Aceptado	Rechazado	Aceptado	Rechazado
VaR sin promedios, NC = 99% y H = 250	Aceptado	Rechazado	Aceptado	Aceptado
VaR con promedios, NC = 99% y H = 250	Aceptado	Aceptado	Aceptado	Aceptado
VaR sin promedios, NC = 99% y H = 500	Aceptado	Aceptado	Aceptado	Aceptado
VaR con promedios, NC = 99% y H = 500	Aceptado	Aceptado	Aceptado	Aceptado