CAPM#
Descargar datos de Yahoo Finance:#
import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
Acciones:
# Definir las acciones y el período de tiempo
stocks = ['KO', 'TSLA', 'WMT', 'FDX']
start = '2019-11-01'
end = '2024-11-01'
# Descargar los datos desde Yahoo Finance
data = yf.download(stocks, start=start, end=end, interval='1mo')['Adj Close'].dropna()
print("Cantidad de datos descargados: ", data.shape)
print(data)
[*******************100%*********************] 4 of 4 completed
Cantidad de datos descargados: (61, 4)
FDX KO TSLA WMT
Date
2019-11-01 146.725632 45.738239 21.996000 36.745743
2019-12-01 138.621567 47.762585 27.888666 36.668610
2020-01-01 133.160736 50.394489 43.371334 35.484848
2020-02-01 129.966156 46.157555 44.532665 33.374165
2020-03-01 111.636307 38.184181 34.933334 35.215202
... ... ... ... ...
2024-07-01 300.776337 66.285568 232.070007 68.444901
2024-08-01 297.313293 71.976555 214.110001 77.010490
2024-09-01 272.345612 71.370712 261.630005 80.750000
2024-10-01 273.850006 65.309998 249.850006 81.949997
2024-11-01 299.970001 63.919998 352.559998 90.440002
[61 rows x 4 columns]
Índice S&P 500 (mercado):
# Definir las acciones y el período de tiempo
market = ['^GSPC']
start = '2019-11-01'
end = '2024-11-01'
# Descargar los datos desde Yahoo Finance
market = yf.download(market, start=start, end=end, interval='1mo')['Adj Close'].dropna()
print("Cantidad de datos descargados: ", market.shape)
print(market)
[*******************100%*********************] 1 of 1 completed
Cantidad de datos descargados: (61,)
Date
2019-11-01 3140.979980
2019-12-01 3230.780029
2020-01-01 3225.520020
2020-02-01 2954.219971
2020-03-01 2584.590088
...
2024-07-01 5522.299805
2024-08-01 5648.399902
2024-09-01 5762.479980
2024-10-01 5705.450195
2024-11-01 5969.339844
Name: Adj Close, Length: 61, dtype: float64
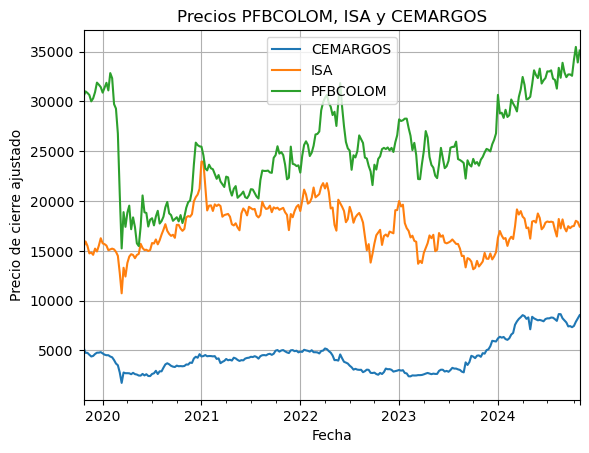
Gráficos de precios:#
# Graficar los precios de las acciones
fig, (ax1, ax3) = plt.subplots(2, 1, figsize=(10, 12))
# Graficar TSLA en el eje primario
ax1.plot(data.index, data['TSLA'], label='TSLA', color='b')
ax1.plot(data.index, data['FDX'], label='FDX', color='black')
ax1.set_xlabel('Fecha')
ax1.set_ylabel('Precio TSLA y FDX (USD)')
ax1.tick_params(axis='y')
# Eje secundario para KO y WMT
ax2 = ax1.twinx()
ax2.plot(data.index, data['KO'], label='KO', color='r')
ax2.plot(data.index, data['WMT'], label='WMT', color='g')
ax2.set_ylabel('Precios de KO y WMT (USD)')
ax2.tick_params(axis='y')
# Título y leyenda del primer gráfico
ax1.set_title('Precios acciones y del mercado')
fig.legend(loc='upper left', bbox_to_anchor=(0.1, 0.9))
ax1.grid(True)
ax1.tick_params(axis='x', rotation=45)
# Graficar los puntos del mercado en el segundo subplot
market = yf.download('^GSPC', start=start, end=end, interval='1mo')['Adj Close'].dropna()
ax3.plot(market.index, market, label='S&P 500', color='b')
ax3.set_xlabel('Fecha')
ax3.set_ylabel('Puntos del mercado')
ax3.set_title('Puntos del S&P 500')
ax3.grid(True)
ax3.tick_params(axis='x', rotation=45)
# Ajuste de diseño
plt.tight_layout()
plt.show()
[*******************100%*********************] 1 of 1 completed
Calcular los rendimientos:#
# Rendimientos mensuales:
returns = data.pct_change().dropna()
market_returns = market.pct_change().dropna()
# Rendimiento esperado:
returns_mean = returns.mean()
market_returns_mean = market_returns.mean()
print("Rendimientos medios de las acciones:\n", returns_mean)
print("Rendimiento medio del mercado:\n", market_returns_mean)
Rendimientos medios de las acciones:
FDX 0.017296
KO 0.007185
TSLA 0.069058
WMT 0.016607
dtype: float64
Rendimiento medio del mercado:
0.012105369746219546
Volatilidades:#
# Volatilidades:
returns_std = returns.std()
market_returns_std = market_returns.std()
print("Volatilidades de las acciones:\n", returns_std)
print("Volatilidad del mercado:\n", market_returns_std)
Volatilidades de las acciones:
FDX 0.103640
KO 0.056229
TSLA 0.223424
WMT 0.054889
dtype: float64
Volatilidad del mercado:
0.05218383687111113
Correlación con respecto al mercado:#
# Correlación de las acciones con el mercado:
correlation = returns.corrwith(market_returns)
print("Correlación de las acciones con el mercado:\n", correlation)
Correlación de las acciones con el mercado:
FDX 0.600219
KO 0.582300
TSLA 0.551162
WMT 0.500216
dtype: float64
Gráficos de rendimientos con respecto al mercado:#
# Gráfico para cada rendimiento de las acciones vs el mercado:
fig, (ax1, ax2, ax3, ax4) = plt.subplots(4, 1, figsize=(10, 16))
# Gráfico de TSLA vs el mercado
ax1.scatter(market_returns, returns['TSLA'], color='black')
ax1.set_ylabel('Rendimiento de TSLA')
ax1.set_xlabel('Rendimiento del mercado')
ax1.set_title('TSLA vs Mercado')
ax1.grid(True)
# Gráfico de FDX vs el mercado
ax2.scatter(market_returns, returns['FDX'], color='black')
ax2.set_ylabel('Rendimiento de FDX')
ax2.set_xlabel('Rendimiento del mercado')
ax2.set_title('FDX vs Mercado')
ax2.grid(True)
# Gráfico de KO vs el mercado
ax3.scatter(market_returns, returns['KO'], color='black')
ax3.set_ylabel('Rendimiento de KO')
ax3.set_xlabel('Rendimiento del mercado')
ax3.set_title('KO vs Mercado')
ax3.grid(True)
# Gráfico de WMT vs el mercado
ax4.scatter(market_returns, returns['WMT'], color='black')
ax4.set_ylabel('Rendimiento de WMT')
ax4.set_xlabel('Rendimiento del mercado')
ax4.set_title('WMT vs Mercado')
ax4.grid(True)
# Ajuste de diseño
plt.tight_layout()
plt.show()
Betas:#
Regresión Lineal:
betas = {}
for stock in stocks:
X = sm.add_constant(market_returns)
model = sm.OLS(returns[stock], X).fit()
betas[stock] = model.params[1]
print("Coeficientes Beta de las acciones:")
for stock, beta in betas.items():
print(f"{stock}: {beta:.4f}")
Coeficientes Beta de las acciones:
KO: 0.6274
TSLA: 2.3598
WMT: 0.5261
FDX: 1.1921
Con coeficientes de correlación:
betas_corr = {}
for stock in stocks:
correlacion = returns[stock].corr(market_returns)
desviacion_stock = returns[stock].std()
desviacion_mercado = market_returns.std()
betas_corr[stock] = correlacion * (desviacion_stock / desviacion_mercado)
print("Coeficientes Beta de las acciones (método de correlación):")
for stock, beta in betas_corr.items():
print(f"{stock}: {beta:.4f}")
Coeficientes Beta de las acciones (método de correlación):
KO: 0.6274
TSLA: 2.3598
WMT: 0.5261
FDX: 1.1921
CAPM:#
Tasa libre de riesgo EE.UU.:
Bonos del Tesoro a 10 Años de EE.UU. (Treasury Bonds):
Es la opción más común, ya que los bonos del Tesoro de EE. UU. se consideran prácticamente libres de riesgo debido a la alta fiabilidad crediticia del gobierno de los Estados Unidos.
Bonos del Tesoro a Corto Plazo (por ejemplo, a 3 meses o 1 año):
A veces se utiliza la tasa de bonos a corto plazo, como los Treasury Bills (T-Bills) de 3 meses, especialmente si se busca una medida más sensible de la tasa libre de riesgo.
T-Bonds:
# Descargar la tasa libre de riesgo (rendimiento de los bonos del Tesoro a 10 años)
risk_free_rate_data = yf.download('^TNX', start=start, end=end, interval='1mo')['Adj Close'].dropna()
# La tasa viene en porcentaje, la convertimos a decimal
risk_free_rate = risk_free_rate_data / 100
print(risk_free_rate.head())
# Rendimiento esperado Rf:
Rf = risk_free_rate.mean()
print("Tasa libre de riesgo:", Rf)
[*******************100%*********************] 1 of 1 completed Date 2019-11-01 0.01776 2019-12-01 0.01919 2020-01-01 0.01520 2020-02-01 0.01127 2020-03-01 0.00698 Name: Adj Close, dtype: float64 Tasa libre de riesgo: 0.024757090850309887
Tasa libre de riesgo Anual, se debe pasar a mensual dado que los precios de las acciones tienen una frecuencia mensual:
# Rf mensual:
Rf = (1 + Rf) ** (1 / 12) - 1
print("Tasa libre de riesgo mensual:", Rf)
Tasa libre de riesgo mensual: 0.002040044729566315
CAPM:
# Calcular el retorno esperado usando CAPM (con rendimiento de bonos del Tesoro a 10 años)
capm_returns_tnx = {}
for stock in stocks:
capm_returns_tnx[stock] = Rf + betas_corr[stock] * (market_returns_mean - Rf)
print("Retornos esperados según el modelo CAPM (Bonos del Tesoro a 10 años):")
for stock, capm_return in capm_returns_tnx.items():
print(f"{stock}: {capm_return:.4f}")
Retornos esperados según el modelo CAPM (Bonos del Tesoro a 10 años):
KO: 0.0084
TSLA: 0.0258
WMT: 0.0073
FDX: 0.0140
T-Bills:
# Descargar la tasa libre de riesgo (rendimiento de los T-Bills a 3 meses)
t_bill_rate_data = yf.download('^IRX', start=start, end=end, interval='1mo')['Adj Close'].dropna()
# La tasa viene en porcentaje, la convertimos a decimal
t_bill_rate = t_bill_rate_data / 100
# Rendimiento esperado anual de Rf:
Rf = t_bill_rate.mean()
# Rf mensual:
Rf = (1 + Rf) ** (1 / 12) - 1
print("Tasa libre de riesgo mensual:", Rf)
[*******************100%*********************] 1 of 1 completed Tasa libre de riesgo mensual: 0.0017872655599009413
# Calcular el retorno esperado usando CAPM (con rendimiento de bonos del Tesoro a 10 años)
capm_returns_tnx = {}
for stock in stocks:
capm_returns_tnx[stock] = Rf + betas_corr[stock] * (market_returns_mean - Rf)
print("Retornos esperados según el modelo CAPM (Bonos del Tesoro a 10 años):")
for stock, capm_return in capm_returns_tnx.items():
print(f"{stock}: {capm_return:.4f}")
Retornos esperados según el modelo CAPM (Bonos del Tesoro a 10 años):
KO: 0.0083
TSLA: 0.0261
WMT: 0.0072
FDX: 0.0141