Funciones de activación¶

Las funciones de activación controlan la información que pasa a través de la red (forward pass).

Las redes neuronales artificiales son capaces de aprender relaciones no lineales gracias a la combinación de funciones de activación no lineales en las múltiples capas.

Las funciones de activación más usadas son sigmoide, ReLU y tangente hiperbólica (tanh), pero existen muchas más y cada vez aparecen nuevas variaciones.

Funciones de Activación en Keras

1. Sigmoide:¶

En Keras: "sigmoid"

\[\sigma(z) = \frac{1}{1+exp^{-z}}\]

Función en forma de S.
Salida en el rango entre 0 y 1, centrada en 0.5.
Comúnmente usada en la capa de salida para problemas de clasificación binaria.

Desventaja:

Cuando las entradas se vuelven pequeñas o grandes la función se concentra en 0 o en 1, llegando a una derivada cercana a 0. Esto conlleva que no tenga gradiente a propagarse en estas zonas a través de la red, por lo que no queda casi nada para las capas inferiores. Esto se conoce como fuga del gradiente.

import numpy as np
import matplotlib.pyplot as plt

sigmoid = lambda z: 1 / (1 + np.exp(-z))

z = np.linspace(-10, 10, 1000)

plt.figure(dpi=100)
plt.plot(z, sigmoid(z));

Derivada:

\[\frac{\partial \sigma(z)}{\partial z} = \sigma(z)(1-\sigma(z))\]

dsigmoid = sigmoid(z) * (1 - sigmoid(z))

plt.figure(dpi=100)
plt.plot(z, dsigmoid, "r-");

2. Tangente hiperbólica:¶

En Keras: "tanh"

\[tanh(z) = \frac{sinh(z)}{cosh(z)}=\frac{exp^z-exp^{-z}}{exp^z+exp^{-z}}\]

Función en forma de S, similar a la función sigmoide.
Salida en el rango entre -1 y 1, centrada en 0.

Desventaja:

Simular a la función sigmoide. Con entradas pequeñas o grandes la función tiene una derivada muy pequeña con tendencia a cero.

tanh = lambda z: (np.exp(z) - np.exp(-z)) / (np.exp(z) + np.exp(-z))

plt.figure(dpi=100)
plt.plot(z, tanh(z));

Derivada:

\[\frac{\partial \tanh(z)}{\partial z} = 1-tan(z)^2\]

dtanh = 1 - tanh(z) ** 2

plt.figure(dpi=100)
plt.plot(z, dtanh, "r-");

3. ReLU:¶

En Keras: "relu"

\[ReLU(z) = max(z,0)\]

ReLU (Rectified Linear Units) es la función de activación más utilizada en el aprendizaje profundo.

Mejor propagación del gradiente: menos problemas de fuga de gradiente en comparación con las funciones de activación sigmoide y thanh.
Cálculo eficiente: ya que solo es comparación, suma y multiplicación.
Presenta varias unidades (neuronas) inactivas porque arroja valores de cero en gran parte de la curva.
Tiene otra gran ventaja en que no tiene valor de salida máximo lo que ayuda a reducir algunos problemas durante el Gradient Descent.

Desventaja:

Es diferenciable en cualquier valor, pero no en 0, el valor de la derivada en este punto puede elegirse arbitrariamente a ser 0 o 1.
Cuando \(z=0\), la pendiente cambia abruptamente, lo que puede ocasionar que el Gradient Descent rebote.
Debido a que no tiene límite superior, es infinito, conduce a veces a nodos inutilizables.

relu = lambda z: np.maximum(z, 0)

plt.figure(dpi=100)
plt.plot(z, relu(z));

Derivada:

Si \(z<0\):

\[\frac{\partial ReLU(z)}{\partial z} = 0\]

Si \(z>0\):

\[\frac{\partial ReLU(z)}{\partial z} = 1\]

drelu = (z > 0) * 1

plt.figure(dpi=100)
plt.plot(z, drelu, "r-");

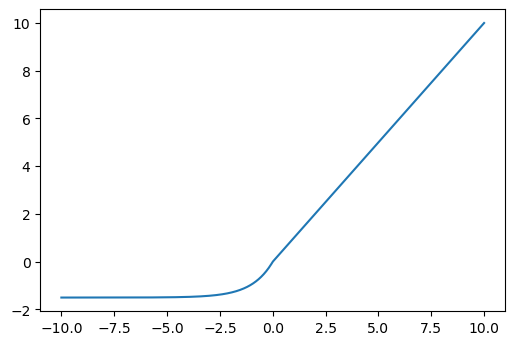
4. ELU:¶

En Keras: "elu"

Si \(z>0\):

\[ELU(z) = z\]

Si \(z<=0\):

\[ELU(z) = \alpha(exp^z-1)\]

ELU (Exponencial Linear Units) es una variación de la función ReLU. Modifica la pendiente de la parte negativa de la función ReLU. Usa una curva logarítmica para definir los valores negativos.

El hiperparámetro \(\alpha\) controla el valor al que se satura una ELU para entradas netas negativas. Los ELU disminuyen el efecto de gradiente de fuga.

Los ELU tienen valores negativos que empujan la media de las activaciones más cerca de cero. Las activaciones medias que están más cerca de cero permiten un aprendizaje más rápido ya que acercan el gradiente al gradiente natural. Los ELU se saturan a un valor negativo cuando el argumento se hace más pequeño. Saturación significa una pequeña derivada que disminuye la variación y la información que se propaga a la siguiente capa.

Desventaja:

Es más lento de calcular que ReLU y sus variantes.

alpha = 1.5

def elu(x):
    if x > 0:
        return x
    else:
        return alpha * (np.exp(x) - 1)

elu = [elu(z) for z in np.linspace(-10, 10, 1000)]

plt.figure(dpi=100)
plt.plot(z, elu);

Derivada:

Si \(z>0\):

\[\frac{\partial ELU(z)}{\partial z} = 1\]

Si \(z<=0\):

\[\frac{\partial ELU(z)}{\partial z} = \alpha exp(z)\]

def delu(x):
    if x > 0:
        return 1
    else:
        return alpha * np.exp(x)

delu = [delu(z) for z in np.linspace(-10, 10, 1000)]

plt.figure(dpi=100)
plt.plot(z, delu, "r-");

5. SELU:¶

En Keras: "selu"

Si \(z>0\):

\[SELU(z) = \lambda z\]

Si \(z<=0\):

\[SELU(z) = \lambda\alpha(exp^z-1)\]

Donde \(\alpha=1.67326324\) y \(\lambda=1.05070098\) son constantes predefinidas.

SELU (Scaled Exponencial Linear Unit) es otra variación de ReLU.

Podría resolver el problema de la fuga y explosión del gradiente con una red compuesta exclusivamente con capas con esta función de activación. La salida de cada capa tendrá a conservar la media cero y desviación estándar de 1.

Desventaja:

Solo para redes neuronales compuestas por capas densas. Puede que no funcione para redes neuronales convolucionales.
Los pesos de cada capa oculta deben inicializarse mediante la inicialización normal de LeCun.
Las variables de entrada (inputs) deben estar normalizadas con media 0 y desviación estándar 1.

alpha = 1.67326324
LAMBDA = 1.05070098

def selu(x):
    if x >= 0:
        return LAMBDA * x
    else:
        return LAMBDA * alpha * (np.exp(x) - 1)

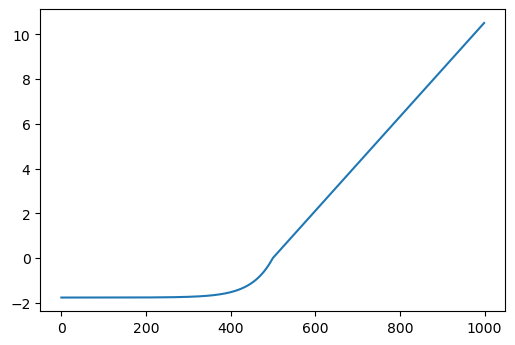
selu = [selu(z) for z in np.linspace(-10, 10, 1000)]

plt.figure(dpi=100)
plt.plot(selu);

Derivada:

Si \(z>0\):

\[\frac{\partial SELU(z)}{\partial z} = \lambda\]

Si \(z<=0\):

\[\frac{\partial SELU(z)}{\partial z} = \lambda\alpha exp^z\]

def dselu(x):
    if x > 0:
        return LAMBDA
    else:
        return LAMBDA * alpha * np.exp(x)

dselu = [dselu(z) for z in np.linspace(-10, 10, 1000)]

plt.figure(dpi=100)
plt.plot(z, dselu, "r-");

6. Softmax:¶

En Keras: "softmax"

\[s(z) = \frac{exp^z}{\sum{exp^z}}\]

Es la forma más generalizada de la función de activación sigmoide. Se utiliza en problemas de clasificación de múltiples clases. Similar a la sigmoide, los elementos del vector de salida están en el rango 0-1, la diferencia es que su suma es igual a 1.

Se utiliza como capa final en los modelos de clasificación porque extraer la probabilidad según los datos de pertenecer a las distintas clases posibles.

Para esta versión de la Softmax, las categorías son excluyentes, es decir, si se asigna una categoría, ya no se puede pertenecer a otra.

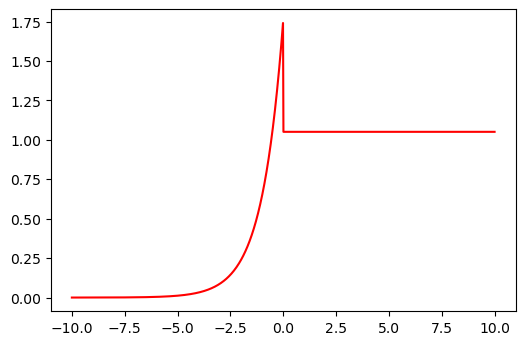
softmax = lambda z: np.exp(z) / sum(np.exp(z))

plt.figure(dpi=100)
plt.plot(z, softmax(z));

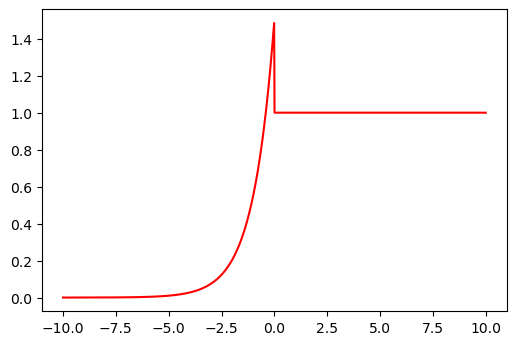
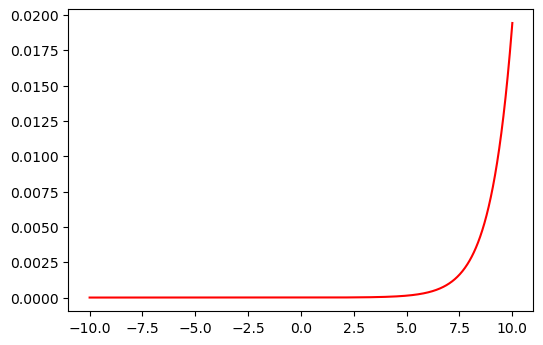
Derivada:

\[\frac{\partial s(z)}{\partial z} = s(z)(1-s(z))\]

dsoftmax = softmax(z) * (1 - softmax(z))

plt.figure(dpi=100)
plt.plot(z, dsoftmax, "r-");

7.Softsing:¶

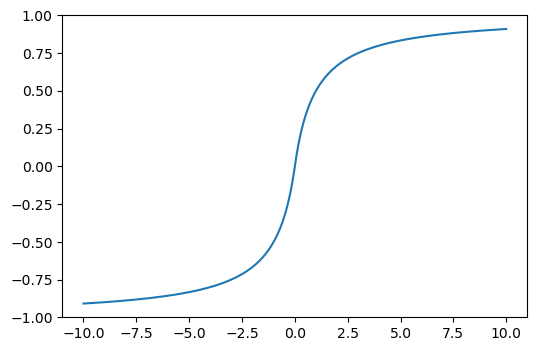
En Keras: "softsign"

\[f(z) = \frac{z}{|z|+1}\]

Es parecida a la tangente hiperbólica, sus valores van de -1 a 1, tiene media 0 y su desviación típica es 1. Es más suavizada que la tangente hiperbólica.

softsing = lambda z: z / (abs(z) + 1)

plt.figure(dpi=100)
plt.plot(z, softsing(z));

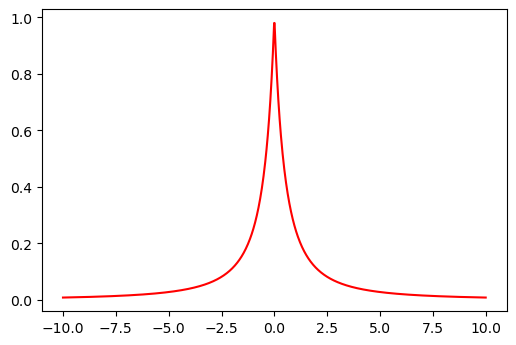
Derivada:

\[\frac{\partial f(z)}{\partial z} = \frac{z}{(|z|+1)^2}\]

dsoftsing = 1 / (abs(z) + 1) ** 2

plt.figure(dpi=100)
plt.plot(z, dsoftsing, "r-");

8. Softplus:¶

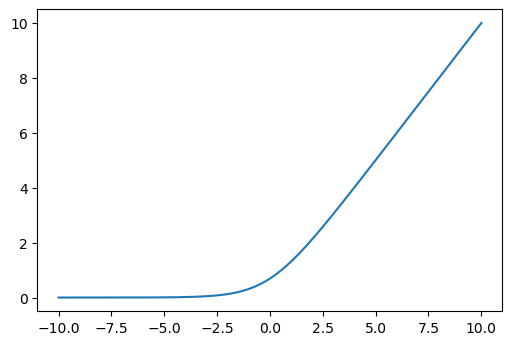
En Keras: "softplus"

Es la función continua y derivable de la función RELU. Esto se consigue mediante el logaritmo. Su gráfica es parecida a la RELU, pero más suavizada.

\[f(z) = ln(exp^z+1)\]

softplus = lambda z: np.log(np.exp(z) + 1)

plt.figure(dpi=100)
plt.plot(z, softplus(z));

Derivada:

\[\frac{\partial f(z)}{\partial z} = \frac{exp(z)}{exp(z)+1} = \frac{1}{exp(-z)+1}\]

dsoftplus = np.exp(z) / (np.exp(z) + 1)

plt.figure(dpi=100)
plt.plot(z, dsoftplus, "r-");

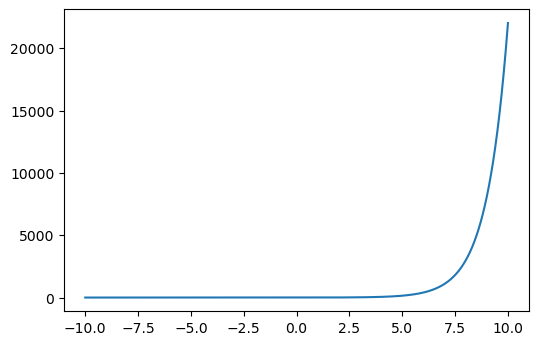
9. Exponencial:¶

En Keras: "exponential"

\[f(z) = exp^z\]

exponential = lambda z: np.exp(z)

plt.figure(dpi=100)
plt.plot(z, exponential(z));

Derivada:

\[\frac{\partial f(z)}{\partial z} = exp(z)\]

dexponential = np.exp(z)

plt.figure(dpi=100)
plt.plot(z, dexponential, "r-");

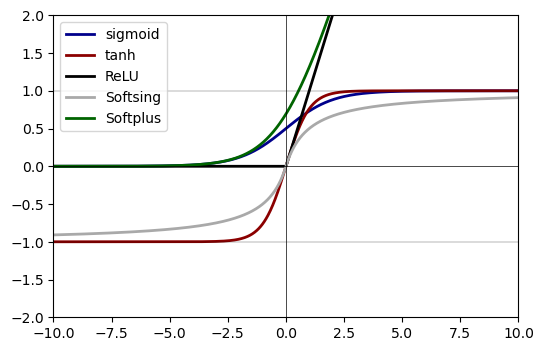
plt.figure(dpi=100)
plt.plot(z, sigmoid(z), label="sigmoid", linewidth=2, color="darkblue")
plt.plot(z, tanh(z), label="tanh", linewidth=2, color="darkred")
plt.plot(z, relu(z), label="ReLU", linewidth=2, color="black")
plt.plot(z, softsing(z), label="Softsing", linewidth=2, color="darkgray")
plt.plot(z, softplus(z), label="Softplus", linewidth=2, color="darkgreen")
plt.xlim(-10, 10)
plt.ylim(-2, 2)
plt.hlines(y=0, xmin=-10, xmax=10, color="black", linewidth=0.5)
plt.vlines(x=0, ymin=-10, ymax=10, color="black", linewidth=0.5)
plt.hlines(y=-1, xmin=-10, xmax=10, color="black", linewidth=0.2)
plt.hlines(y=1, xmin=-10, xmax=10, color="black", linewidth=0.2)
plt.legend();

plt.figure(dpi=100)
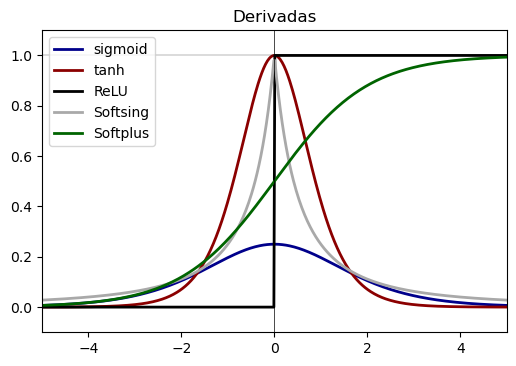
plt.plot(z, dsigmoid, label="sigmoid", linewidth=2, color="darkblue")
plt.plot(z, dtanh, label="tanh", linewidth=2, color="darkred")
plt.plot(z, drelu, label="ReLU", linewidth=2, color="black")
plt.plot(z, dsoftsing, label="Softsing", linewidth=2, color="darkgray")
plt.plot(z, dsoftplus, label="Softplus", linewidth=2, color="darkgreen")
plt.xlim(-5, 5)
plt.ylim(-0.1, 1.1)
plt.vlines(x=0, ymin=-10, ymax=10, color="black", linewidth=0.5)
plt.hlines(y=-1, xmin=-10, xmax=10, color="black", linewidth=0.2)
plt.hlines(y=1, xmin=-10, xmax=10, color="black", linewidth=0.2)
plt.title("Derivadas")
plt.legend();

plt.figure(dpi=100)
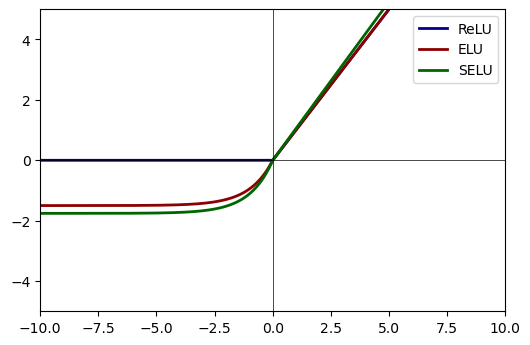
plt.plot(z, relu(z), label="ReLU", linewidth=2, color="darkblue")
plt.plot(z, elu, label="ELU", linewidth=2, color="darkred")
plt.plot(z, selu, label="SELU", linewidth=2, color="darkgreen")
plt.xlim(-10, 10)
plt.ylim(-5, 5)
plt.hlines(y=0, xmin=-10, xmax=10, color="black", linewidth=0.5)
plt.vlines(x=0, ymin=-10, ymax=10, color="black", linewidth=0.5)
plt.legend();

plt.figure(dpi=100)
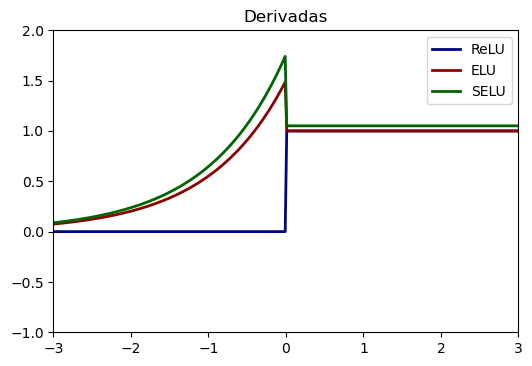
plt.plot(z, drelu, label="ReLU", linewidth=2, color="darkblue")
plt.plot(z, delu, label="ELU", linewidth=2, color="darkred")
plt.plot(z, dselu, label="SELU", linewidth=2, color="darkgreen")
plt.xlim(-3, 3)
plt.ylim(-1, 2)
plt.title("Derivadas")
plt.legend();