VaR método Delta-Normal o varianzas-covarianzas#

Importar datos.#

datos = read.csv("Cuatro acciones 2020.csv", sep = ";", dec = ",", header = T)

Matriz de precios.#

Crear una matriz con los valores de los precios de las acciones: [,-1] elimina la primera columna de la matriz datos que corresponde a las fechas. Quedan solo los precios.

precios = datos[,-1]

head(precios)
A data.frame: 6 × 4
ECOPFAVALISANUTRESA
<int><int><int><int>
1277511651308025720
2264511551308025700
3261511651332025980
4269011651342025920
5273011751366025920
6274011901356025840
 
precios = ts(precios)

dim(precios)
  1. 500
  2. 4

Se cargaron cuatro acciones y 500 precios por acción.

Nombres de las acciones.#

nombres = colnames(precios)
nombres
  1. 'ECO'
  2. 'PFAVAL'
  3. 'ISA'
  4. 'NUTRESA'

Número de acciones.#

acciones = ncol(precios)
acciones
4

Matriz de rendimientos.#

\[Rendimiento_t=log\frac{Precio_t}{Precio_{t-1}}\]
\[log\frac{Precio_t}{Precio_{t-1}}=log(Precio_t)-log(Precio_{t-1})\]
rendimientos = diff(log(precios))

dim(rendimientos)
  1. 499
  2. 4

Hay 499 rendimientos por acción.

\(S_0:\)Precio actual de cada acción.#

s = tail(precios,1)
s = as.numeric(s)
s
  1. 2220
  2. 955
  3. 18000
  4. 22500

El precio de ECO es de 2.220 COP, de PFAVAL 955 COP, ISA de 18.000 COP y NUTRESA de 22.500 COP.

Número de acciones del portafolio de inversión.#

numero_acciones = c(180000,5000,12000,9000)
numero_acciones
  1. 180000
  2. 5000
  3. 12000
  4. 9000

Valor de mercado de cada acción.#

valor_mercado_acciones = numero_acciones*s
valor_mercado_acciones
  1. 399600000
  2. 4775000
  3. 2.16e+08
  4. 202500000

ECO: $ 399.600.000.

PFAVAL: $ 4.775.000.

ISA: $ 216.000.000.

NUTRESA: $ 202.500.000.

Valor de mercado del portafolio de inversión.#

valor_portafolio = sum(valor_mercado_acciones)
valor_portafolio
822875000

El portafolio de inversión está valorado en $ 822.875.000.

Proporciones de inversión.#

proporciones = valor_mercado_acciones/valor_portafolio
proporciones
  1. 0.485614461491721
  2. 0.00580282545951694
  3. 0.262494303509038
  4. 0.246088409539724

ECO: 48,56%.

PFAVAL: 0,580%.

ISA: 26,25%.

NUTRESA: 24,61%.

\[\sum_{i=1}^nw_i=1\]
sum(proporciones)
1

\(\mu:\) Rendimiento esperado de cada acción.#

rendimientos_esperados = apply(rendimientos,2,mean)
rendimientos_esperados
ECO
-0.000447181465559539
PFAVAL
-0.000398326704447035
ISA
0.000639854532799824
NUTRESA
-0.000268043266851791

ECO: -0,0447% diario.

PFAVAL: -0,0398% diario.

ISA: 0,0640% diario.

NUTRESA: -0,0268% diario.

\(\sigma:\)Volatilidad de cada acción.#

volatilidades = apply(rendimientos,2,sd)
volatilidades
ECO
0.0319324424190137
PFAVAL
0.0285577211893029
ISA
0.0237292026947701
NUTRESA
0.0140104740592151

ECO: 3,193% diaria.

PFAVAL: 2,856% diaria.

ISA: 2,373% diaria.

NUTRESA: 1,401% diaria.

Matriz varianzas-covarianzas.#

covarianzas = cov(rendimientos)
covarianzas
A matrix: 4 × 4 of type dbl
ECOPFAVALISANUTRESA
ECO0.00101968090.00059394680.00011603270.0001493216
PFAVAL0.00059394680.00081554340.00015643600.0001322689
ISA0.00011603270.00015643600.00056307510.0001519996
NUTRESA0.00014932160.00013226890.00015199960.0001962934

Coeficientes de correlación.#

correlacion = cor(rendimientos)
correlacion
A matrix: 4 × 4 of type dbl
ECOPFAVALISANUTRESA
ECO1.00000000.65131610.15313170.3337626
PFAVAL0.65131611.00000000.23085010.3305836
ISA0.15313170.23085011.00000000.4572004
NUTRESA0.33376260.33058360.45720041.0000000

Rendimientos del portafolio de inversión.#

\[R_P=\sum_{i=1}^nw_iR_i\]
rendimientos_portafolio = vector()

for(i in 1:nrow(rendimientos)){

  rendimientos_portafolio[i] = sum(rendimientos[i,]*proporciones)

}

Rendimiento esperado del portafolio de inversión.#

rendimiento_esperado_portafolio = mean(rendimientos_portafolio)
rendimiento_esperado_portafolio
-0.000117473378221543

Rendimientos esperado del portafolio de inversión diario de -0,012%.

Volatilidad del portafolio de inversión.#

volatilidad_portafolio = sd(rendimientos_portafolio)
volatilidad_portafolio
0.0195008972788864

Volatilidad del portafolio de inversión diaria de 1,950%.

Volatilidad del portafolio a partir de la matriz de varianzas-covarianzas.#

volatilidad_portafolio = sqrt(sum(t(proporciones)%*%covarianzas*proporciones))
volatilidad_portafolio
0.0195008972788864

Volatilidad del portafolio de inversión diaria de 1,950%.

VaR (sin promedios)#

Nivel de confianza, NC, del 99% y horizonte de tiempo, t, de 10 días. Estos días representan dos semanas.

La frecuencia de los datos es diaria, por tanto t = 10.

NC = 0.99
t = 10
\[\alpha=0,01\]
1

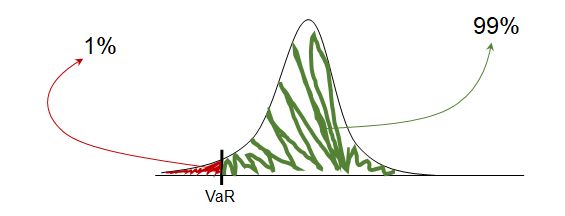
1#

En la distribución normal con \(\mu=0\), se cumple que:

\[|Z_{\alpha=0,01}|=Z_{NC=0,99}\]

VaR individuales (sin promedios) [%].#

\[VaR=Z_{\alpha}\sigma\sqrt{(t)}\]
VaR_individuales_sin_promedios_porcentaje = volatilidades*qnorm(NC)*sqrt(t)
VaR_individuales_sin_promedios_porcentaje
ECO
0.234912861922595
PFAVAL
0.210086529759846
ISA
0.17456525382633
NUTRESA
0.103068863789222

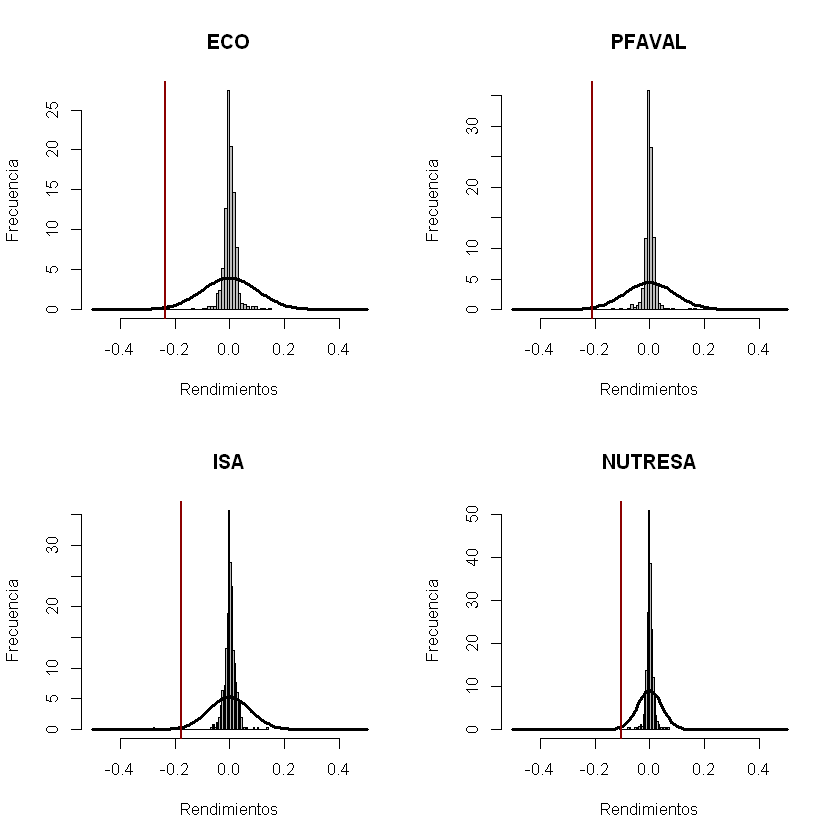
  • Con un nivel de confianza del 99%, el VaR diario de ECO es de 23,49%.

  • Con una probabilidad del 99%, se espera perder 21,01% o menos cada día con la acción de PFAVAL.

  • Con una probabilidad del 1%, se espera perder más de 17,46% cada día con la acción de ISA.

  • De cada 100 días, se espera que en un (1) día se pierda más de 10,31% con la acción de NUTRESA y 99 días perder 10,31% o menos.

VaR individuales (sin promedios) [$].#

\[VaR=Z_{\alpha}\sigma V_0\sqrt{(t)}\]
VaR_individuales_sin_promedios = valor_mercado_acciones*volatilidades*qnorm(NC)*sqrt(t)
VaR_individuales_sin_promedios
ECO
93871179.624269
PFAVAL
1003163.17960326
ISA
37706094.8264872
NUTRESA
20871444.9173174

Conclusión:#

  • Con un nivel de confianza del 99%, el VaR diario de ECO es de 93.871.179,62 COP.

  • Con una probabilidad del 99%, se espera perder 1.003.163,18 COP o menos cada día con la acción de PFAVAL.

  • Con una probabilidad del 1%, se espera perder más de 37.706.094,83 COP cada día con la acción de ISA.

  • De cada 100 días, se espera que en un (1) día se pierda más de 20.871.444,92 COP con la acción de NUTRESA y 99 días perder 20.871.444,92 COP o menos.

El vector VaR_individuales_sin_promedios está vertical.

VaR portafolio de inversión (sin promedios) [$].#

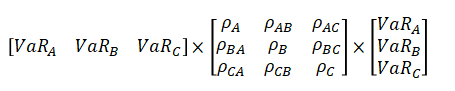
\[VaR_P=\sqrt{\sum_{i=1}^nVaR_i^2+2\sum_{i<j}VaR_iVaR_j\rho_{i,j}}\]
2

2#

\[VaR_P=\sqrt{[VaR]C[VaR]^T}\]

Se transpone el vector VaR_individuales_sin_promedios al principio de la ecuación porque está vertical y debe ser primero horizontal. Al final de la ecuación debe estar vertical.

Para transponer se usa la función t.

\(C:\) Matríz de correlaciones.

\(VaR:\) vector fila de los VaR individuales.

\(VaR^T:\) vector de los VaR individuales transpuesto.

VaR_portafolio_sin_promedios = sqrt(sum(t(VaR_individuales_sin_promedios)%*%correlacion*VaR_individuales_sin_promedios))
VaR_portafolio_sin_promedios
118049219.741064

Conclusión:#

  • Con un nivel de confianza del 99%, el VaR diario del portafolio de inversión es de 118.049.219,74 COP.

  • Con una probabilidad del 99%, se espera perder 118.049.219,74 COP o menos cada día en el portafolio de inversión.

  • Con una probabilidad del 1%, se espera perder más de 118.049.219,74 COP cada día en el portafolio de inversión.

  • De cada 100 días, se espera que en un (1) día se pierda más de 20.871.444,92 COP con la acción de NUTRESA y 99 días perder 20.871.444,92 COP o menos.

VaR portafolio de inversión (sin promedios) [%].#

VaR_portafolio_sin_promedios_porcentaje = VaR_portafolio_sin_promedios/valor_portafolio
VaR_portafolio_sin_promedios_porcentaje
0.143459480165352

Conclusión:#

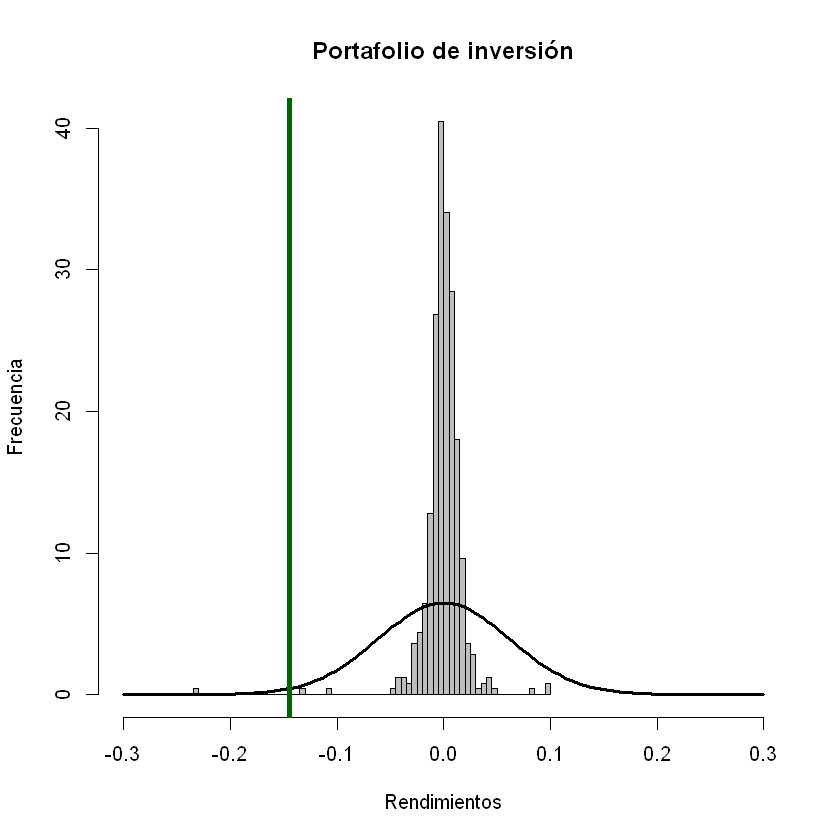
  • Con un nivel de confianza del 99%, el VaR diario del portafolio de inversión es de 14,35%.

  • Con una probabilidad del 99%, se espera perder 14,35% o menos cada día en el portafolio de inversión.

  • Con una probabilidad del 1%, se espera perder más de 14,35% cada día en el portafolio de inversión.

  • De cada 100 días, se espera que en un (1) día se pierda más de 20.871.444,92 COP con la acción de NUTRESA y 99 días perder 20.871.444,92 COP o menos.

Sumatoria de los VaR.#

suma_VaR_individuales_sin_promedios = sum(VaR_individuales_sin_promedios)
suma_VaR_individuales_sin_promedios
153451882.547677

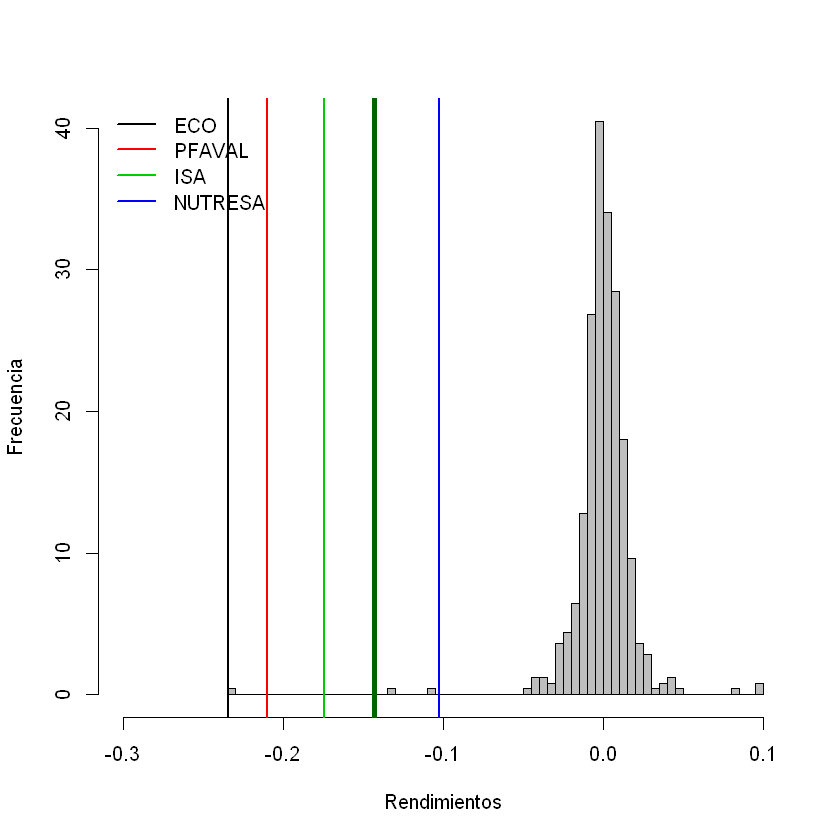
Suponiendo que las acciones no conforman un portafolio de inversión, la sumatoria de los VaR individuales es de 153.451.882,54 COP; sin embargo, como las acciones están en un portafolio de inversión, el VaR del portafolio de inversión con un nivel de confianza del 99% es de 118.049.219,74 COP.

La diferencia entre los VaR individuales sumados y el VaR resultante del portafolio de inversión se conoce como Beneficio por diversificación (BD).

Beneficio por diversificación (BD)#

El VaR global es menor o igual que la suma de los VaR individuales.

\[VaR \leq \sum_{i=1}^nVaR_i\]
\[BD = \sum_{i=1}^n VaR_i - VaR_P\]
BD_sin_promedios = suma_VaR_individuales_sin_promedios - VaR_portafolio_sin_promedios
BD_sin_promedios
35402662.8066126

El Beneficio por diversificación (BD) indica cuánto es el beneficio por diversificar el portafolio de inversión con las acciones.

Con un nivel de confianza del 99%, el BD diario es de 35.402.662,81 COP. Cada día dejaría de perder 35.402.662,81 COP en el portafolio de inversión.

VaR (con promedios)#

En la distribución normal con \(\mu\neq0\):

\[|Z_{\alpha=0.01}|\neq Z_{NC=0.99}\]

Nivel de confianza, NC, del 99% y horizonte de tiempo, t, de 10 días. Estos días representan dos semanas.

La frecuencia de los datos es diaria, por tanto t = 10.

NC = 0.99
t = 10

VaR individuales (con promedios) [%].#

\[VaR = |\mu + Z_{\alpha} \sigma|\]
VaR_individuales_con_promedios_porcentaje = abs(rendimientos_esperados*t+qnorm(1-NC, sd = volatilidades*sqrt(t)))
VaR_individuales_con_promedios_porcentaje
ECO
0.23938467657819
PFAVAL
0.214069796804316
ISA
0.168166708498332
NUTRESA
0.10574929645774

VaR individuales (con promedios) [$].#

\[VaR = |\mu + Z_{\alpha} \sigma V_0|\]
VaR_individuales_con_promedios = valor_mercado_acciones*abs(rendimientos_esperados*t+qnorm(1-NC, sd = volatilidades*sqrt(t)))
VaR_individuales_con_promedios
ECO
95658116.7606449
PFAVAL
1022183.27974061
ISA
36324009.0356396
NUTRESA
21414232.5326923

VaR portafolio de inversión (con promedios) [$].#

Se transpone el vector VaR_individuales_con_promedios al principio de la ecuación porque está vertical y debe ser primero horizontal. Al final de la ecuación debe estar vertical.

Para transponer se usa la función t.

VaR_portafolio_con_promedios = sqrt(sum(t(VaR_individuales_con_promedios)%*%correlacion*VaR_individuales_con_promedios))
VaR_portafolio_con_promedios
119295160.239381

VaR portafolio de inversión (con promedios) [%].#

VaR_portafolio_con_promedios_porcentaje = VaR_portafolio_con_promedios/valor_portafolio
VaR_portafolio_con_promedios_porcentaje
0.144973611106646

Sumatoria de los VaR.#

suma_VaR_individuales_con_promedios = sum(VaR_individuales_con_promedios)
suma_VaR_individuales_con_promedios
154418541.608717

Beneficio por diversificación (BD)#

BD_con_promedios = suma_VaR_individuales_con_promedios - VaR_portafolio_con_promedios
BD_con_promedios
35123381.3693362

Otra forma de calcular el VaR (sin promedios)#

Esta forma es a partir de las proporciones de inversión, proporciones, y la matriz varianzas-covarianzas, covarianzas.

El vector proporciones está vertical, se debe transponer al principio de la ecuación.

Volatilidad del portafolio a partir de la matriz de varianzas-covarianzas#

vol_portafolio = sqrt(sum(t(proporciones)%*%covarianzas*proporciones))
vol_portafolio
0.0195008972788864

VaR portafolio de inversión (sin promedios) [$].#

VaR_portafolio_sin_promedios = valor_portafolio*vol_portafolio*qnorm(NC)*sqrt(t)
VaR_portafolio_sin_promedios
118049219.741064

Este valor es igual al calculado anteriormente a partir de los VaR individuales (sin promedio).

Gráficos#

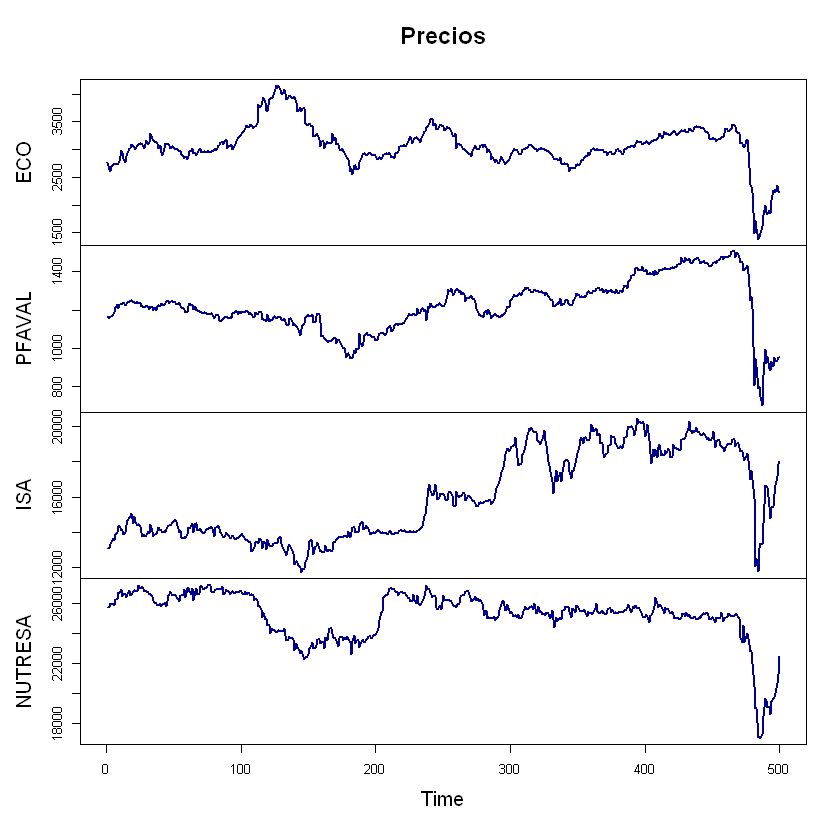
Precios de las acciones.#

plot(precios, col = "darkblue", lwd = 2, main = "Precios")
../../../_images/output_123_0.png

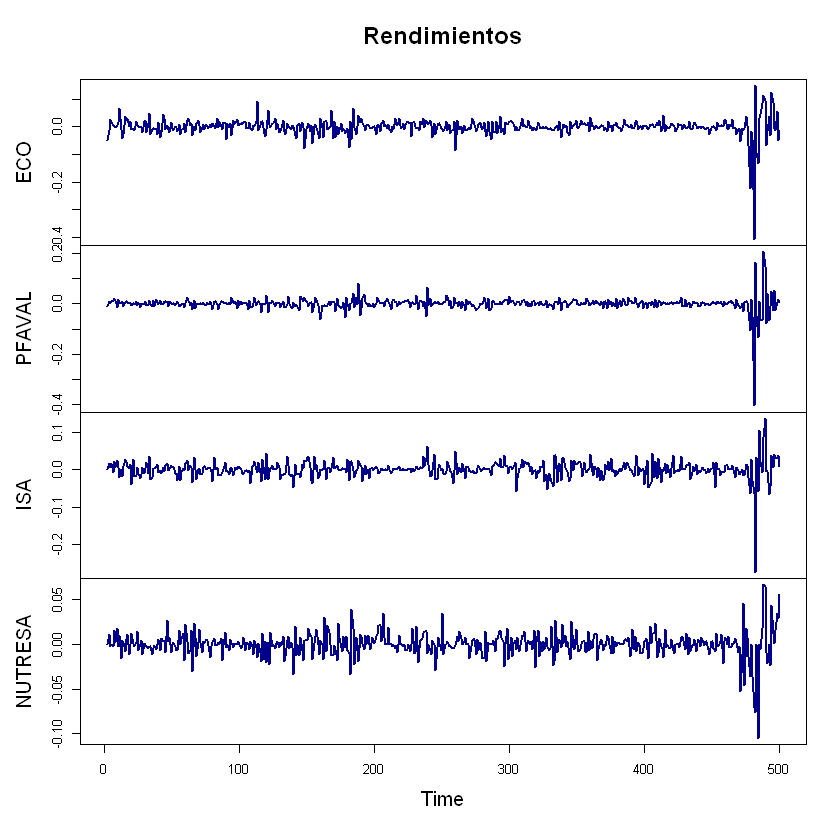
Rendimientos de las acciones.#

plot(rendimientos, col = "darkblue", lwd = 2, main = "Rendimientos")
../../../_images/output_125_0.png

Histograma, distribución normal y VaR (sin promedios) de las acciones.#

layout(matrix(c(1:4), nrow = 2, byrow = T))
# layout.show(4)  correr esta línea en RStudio.

for(i in 1:acciones){

  hist(rendimientos[,i], breaks = 60, col= "gray", xlab = "Rendimientos", ylab = "Frecuencia", main = nombres[i], freq = F, xlim = c(-0.5, 0.5))
  curve(dnorm(x, mean = 0, sd = volatilidades[i]*sqrt(t)), add = T, lwd = 3)
  abline(v = - VaR_individuales_sin_promedios_porcentaje[i], col = "darkred", lwd = 2)

}
../../../_images/output_127_0.png

Histograma, distribución normal y VaR (sin promedios) del portafolio de inversión.#

hist(rendimientos_portafolio, breaks = 60, col = "gray", xlab = "Rendimientos", ylab = "Frecuencia", main = "Portafolio de inversión", freq=F, xlim = c(-0.3, 0.3))
curve(dnorm(x, mean = 0, sd = volatilidad_portafolio*sqrt(t)), add = T, lwd = 3)
abline(v = -VaR_portafolio_con_promedios_porcentaje, col = "darkgreen", lwd = 4)
../../../_images/output_129_0.png

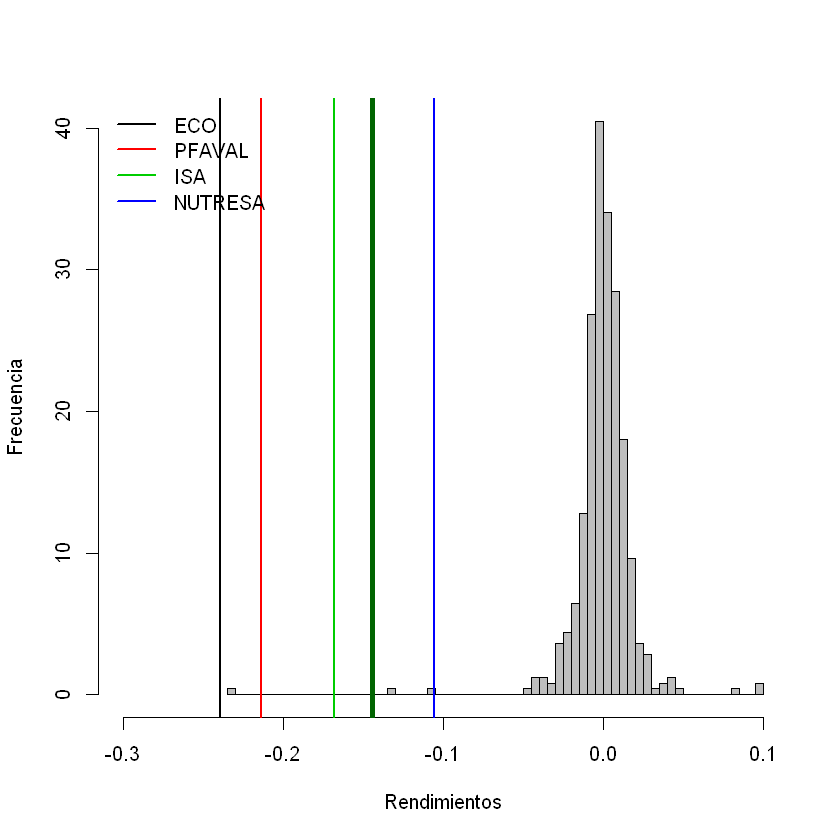
Comparación VaR (sin promedios).#

hist(rendimientos_portafolio, breaks = 60, col = "gray", xlab = "Rendimientos", ylab = "Frecuencia", main = "", freq=F, xlim = c(-0.3,0.1))
for(i in 1:acciones){

abline(v = - VaR_individuales_sin_promedios_porcentaje[i], col = i, lwd = 2)

}
abline(v = -VaR_portafolio_sin_promedios_porcentaje, col = "darkgreen", lwd = 4)
legend("topleft", nombres, lty = rep(1, times = acciones), lwd = rep(2, times = acciones), col = seq(1, acciones), bty = "n")
../../../_images/output_131_0.png

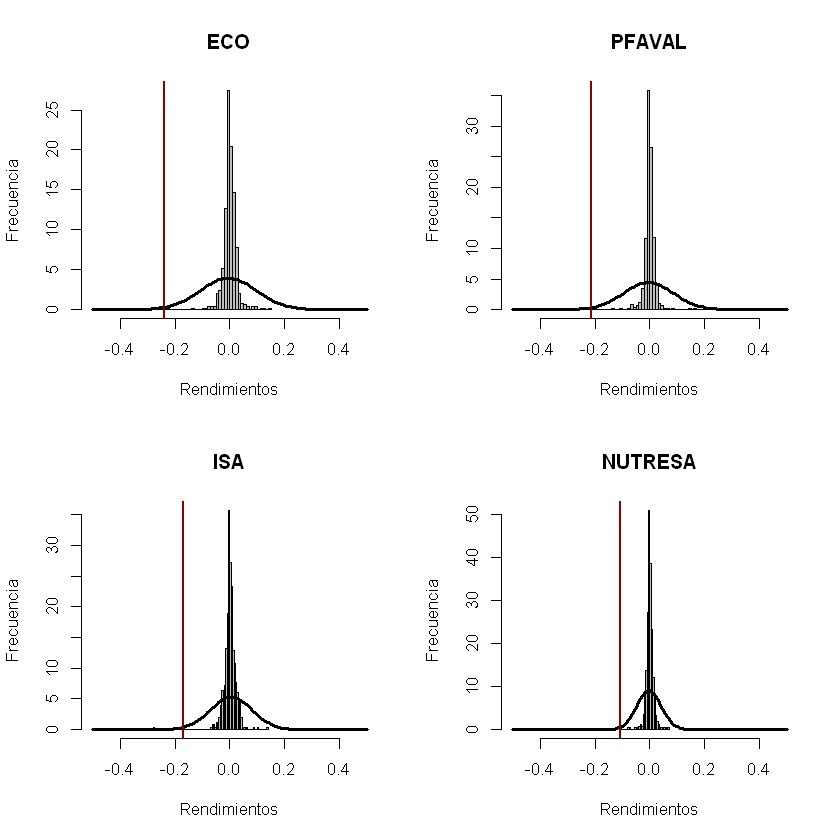
Histograma, distribución normal y VaR (con promedios) de las acciones.#

layout(matrix(c(1:4), nrow = 2, byrow = T))
# layout.show(4)  correr esta línea en RStudio.

for(i in 1:acciones){

  hist(rendimientos[,i], breaks = 60, col= "gray", xlab = "Rendimientos", ylab = "Frecuencia", main = nombres[i], freq = F, xlim = c(-0.5, 0.5))
  curve(dnorm(x, mean = rendimientos_esperados[i]*t, sd = volatilidades[i]*sqrt(t)), add = T, lwd = 3)
  abline(v = - VaR_individuales_con_promedios_porcentaje[i], col = "darkred", lwd = 2)

}
../../../_images/output_133_0.png

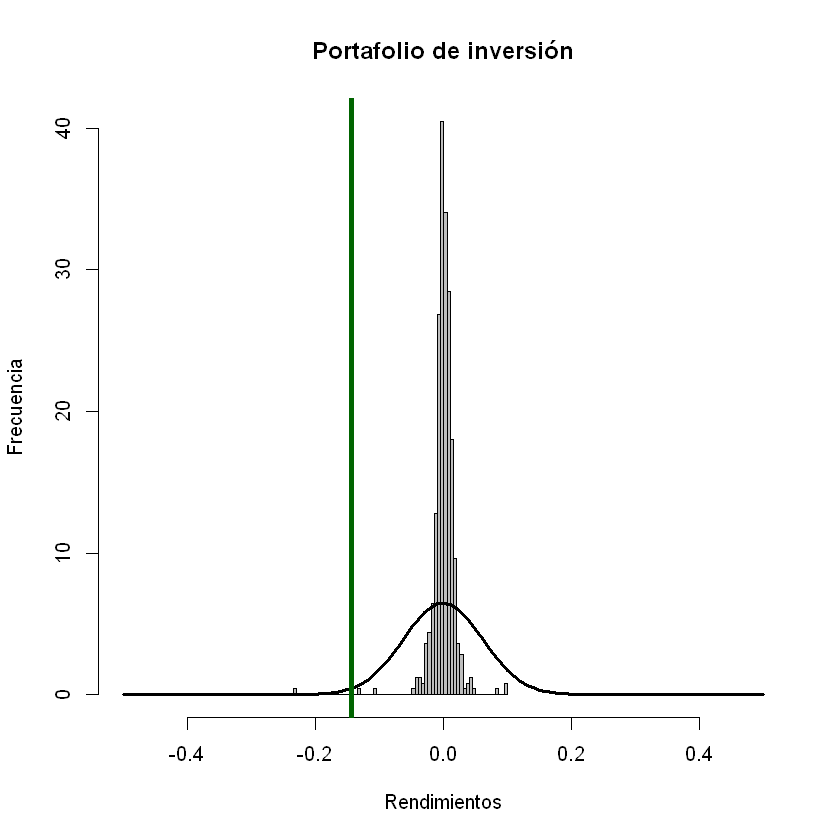
Histograma, distribución normal y VaR (con promedios) del portafolio de inversión.#

hist(rendimientos_portafolio, breaks = 60, col = "gray", xlab = "Rendimientos", ylab = "Frecuencia", main = "Portafolio de inversión", freq=F, xlim = c(-0.5, 0.5))
curve(dnorm(x, mean = rendimiento_esperado_portafolio*t, sd = volatilidad_portafolio*sqrt(t)), add = T, lwd = 3)
abline(v = -VaR_portafolio_con_promedios_porcentaje, col = "darkgreen", lwd = 4)
../../../_images/output_135_0.png

Comparación VaR (con promedios).#

hist(rendimientos_portafolio, breaks = 60, col = "gray", xlab = "Rendimientos", ylab = "Frecuencia", main = "", freq=F, xlim = c(-0.3,0.1))
for(i in 1:acciones){

abline(v = - VaR_individuales_con_promedios_porcentaje[i], col = i, lwd = 2)

}
abline(v = -VaR_portafolio_con_promedios_porcentaje, col = "darkgreen", lwd = 4)
legend("topleft", nombres, lty = rep(1, times = acciones), lwd = rep(2, times = acciones), col = seq(1, acciones), bty = "n")
../../../_images/output_137_0.png