Simulación estrategia de cobertura

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# Leer el archivo CSV, ajustando el formato de los números
df = pd.read_csv("TRM.csv", delimiter=";")
df["Fecha"] = pd.to_datetime(df["Fecha"], format="%d/%m/%Y")
df["Precio"] = (
    df["Precio"]
    .str.replace(".", "", regex=False)
    .str.replace(",", ".", regex=False)
    .astype(float)
)

# Calcular los rendimientos logarítmicos para el gráfico
rendimientos_log = np.log(df["Precio"] / df["Precio"].shift(1))

# Crear figuras para los gráficos
fig, ax = plt.subplots(2, 1, figsize=(12, 8))

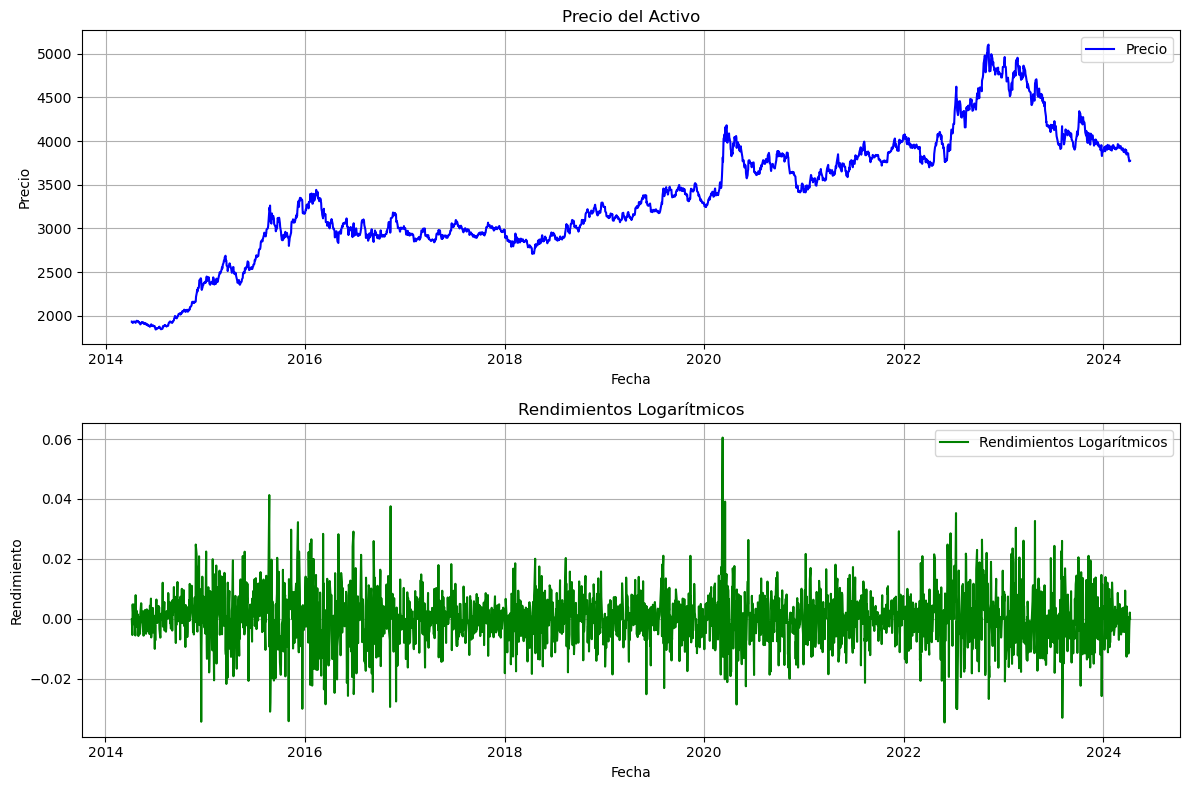
# Gráfico de los precios
ax[0].plot(df["Fecha"], df["Precio"], label="Precio", color="blue")
ax[0].set_title("Precio del Activo")
ax[0].set_xlabel("Fecha")
ax[0].set_ylabel("Precio")
ax[0].legend()
ax[0].grid(True)

# Gráfico de los rendimientos logarítmicos
ax[1].plot(
    df["Fecha"], rendimientos_log, label="Rendimientos Logarítmicos", color="green"
)
ax[1].set_title("Rendimientos Logarítmicos")
ax[1].set_xlabel("Fecha")
ax[1].set_ylabel("Rendimiento")
ax[1].legend()
ax[1].grid(True)

plt.tight_layout()
plt.show()

# Calcular las tasas de retorno logarítmicas y sus parámetros
precios = df["Precio"].values
mu = rendimientos_log.mean()  # Promedio de la tasa de retorno logarítmica
sigma = rendimientos_log.std()  # Volatilidad

print("Rentabilidad esperada diaria:", mu)
print("Volatilidad diaria:", sigma)
print("Precio más reciente:", precios[-1])
print("Fecha más reciente:", df["Fecha"].iloc[-1])

Rentabilidad esperada diaria: 0.00025622779632233206
Volatilidad diaria: 0.008763742455745923
Precio más reciente: 3774.86
Fecha más reciente: 2024-04-08 00:00:00

Simulación diaria hasta un mes:

# Función para simular múltiples trayectorias usando el modelo GBM
def simular_gbm(S0, mu, sigma, T, dt, num_trayectorias, seed=None):
    """
    Simula múltiples trayectorias de un Movimiento Browniano Geométrico.

    Parámetros:
    - S0: Precio inicial del activo.
    - mu: Tasa de retorno logarítmica media.
    - sigma: Volatilidad del activo.
    - T: Tiempo total de simulación.
    - dt: Paso de tiempo de la simulación.
    - num_trayectorias: Número de trayectorias a simular.
    - seed: Semilla para el generador de números aleatorios (opcional).

    Retorna:
    - t: Vector de tiempos de simulación.
    - S: Array con las trayectorias simuladas del precio del activo.
    """
    if seed is not None:
        np.random.seed(seed)  # Establecer la semilla para reproducibilidad

    n = int(T / dt)  # Número de pasos en el tiempo
    t = np.linspace(0, T, n)
    S = np.zeros((n, num_trayectorias))
    S[0] = S0

    for i in range(1, n):
        Z = np.random.standard_normal(num_trayectorias)  # Genera variaciones aleatorias
        S[i] = S[i - 1] * np.exp((mu - 0.5 * sigma**2) * dt + sigma * np.sqrt(dt) * Z)

    return t, S


# Parámetros de la simulación
S0 = df["Precio"].iloc[-1]  # Precio inicial: último precio conocido
T = 30  # Tiempo total de simulación (30 días para llegar al mes)
dt = 1  # Paso de tiempo (saltos diarios)
num_trayectorias = 10000  # Número de trayectorias a simular
seed = 52  # Semilla para la reproducibilidad

# Simular las trayectorias y visualizar
t, trayectorias_simuladas = simular_gbm(S0, mu, sigma, T, dt, num_trayectorias, seed)
plt.figure(figsize=(10, 6))
for i in range(num_trayectorias):
    plt.plot(t, trayectorias_simuladas[:, i], linewidth=1, alpha=0.5)

plt.xlabel("Tiempo (años)")
plt.ylabel("Precio del activo")
plt.title("Simulación GBM para Ecopetrol (saltos mensuales por 6 meses)")
plt.grid(True)
plt.show()

# Get the last column of the array
last_time_prices = trayectorias_simuladas[-1, :]

# Create a histogram
plt.hist(last_time_prices, bins=30)
plt.xlabel("Price")
plt.ylabel("Frequency")
plt.title("Histograma de los precios simulados en el día 30")
plt.show()

Valoración de Opción Financiera de compra:

La serie de tiempo tiene frecuencia diaria, así que las tasas del mercado se convertirán a diarias.

# Datos de las tasas libres de riesgo:
rd = 0.12121  # E.A. (IBR para 1 mes)
rf = 0.0532999  # Nominal Anual (SOFR para 1 mes)
# Conversión de tasas diarias.
rd = np.log(1 + rd ) / 365  # C.C.D.
rf = np.log(1 + rf / 12) / 30  # C.C.D.

def valorar_opcion_divisa_call(S0, K, T, rd, rf, sigma, num_simulaciones):
    if seed is not None:
        np.random.seed(seed)  # Establecer la semilla

    dt = T  # Asumimos un paso de tiempo hasta el vencimiento
    Z = np.random.standard_normal(num_simulaciones)
    ST = S0 * np.exp((rd - rf - 0.5 * sigma**2) * dt + sigma * np.sqrt(dt) * Z)

    payoff_call = np.maximum(ST - K, 0)  # Para Put sería np.maximum(K - ST , 0)
    V0 = np.exp(-rd * T) * np.mean(payoff_call)

    return V0

Opción de compra europea con vencimiento en un mes. Opción ATM.

# Parámetros de la opción sobre divisas
K = S0  # Precio de ejercicio (Opción ATM)
num_simulaciones = 10000  # Número de simulaciones
seed = 52

precio_opcion_call = valorar_opcion_divisa_call(
    S0, K, T, rd, rf, sigma, num_simulaciones
)
print("El precio de la opción de compra sobre divisas es:", precio_opcion_call)

El precio de la opción de compra sobre divisas es: 80.81584142899695

Simulación estrategia de cobertura con Opción Call:

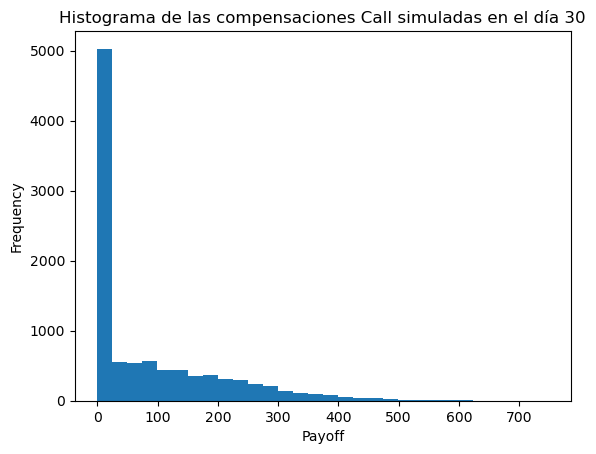
Compensaciones en el último período simulado.

payoff_call_T = np.maximum(last_time_prices - K, 0)

# Create a histogram
plt.hist(payoff_call_T, bins=30)
plt.xlabel("Payoff")
plt.ylabel("Frequency")
plt.title("Histograma de las compensaciones Call simuladas en el día 30")
plt.show()

Cantidad de escenarios donde se ejerce la opción:

ejercer = np.sum(last_time_prices > K)
print("Cantidad de escenarios donde se ejerce:", ejercer)
print("Probabilidad de ejercer la Call:", ejercer / num_trayectorias)

Cantidad de escenarios donde se ejerce: 5519
Probabilidad de ejercer la Call: 0.5519

Precios con cobertura:

hedge_price = np.abs(-last_time_prices + payoff_call_T - precio_opcion_call)

# Create a histogram
plt.hist(hedge_price, bins=30)
plt.xlabel("Price")
plt.ylabel("Frequency")
plt.title("Histograma de los precios con cobertura en el día 30")
plt.show()

Resultados de la simulación de la cobertura:

from scipy import stats
import numpy as np

# Calculate the most frequently occurring price
mode_hedge_price = stats.mode(hedge_price)[0]

# Calculate the volatility
vol_hedge_price = np.std(hedge_price)
vol_price = np.std(last_time_prices)

print("Precio promedio sin cobertura:", np.mean(last_time_prices))
print("Volatilidad escenario sin cobertura:", vol_price)
print("Precio más probable con cobertura:", mode_hedge_price)
print("Volatilidad escenario con cobertura:", vol_hedge_price)

Precio promedio sin cobertura: 3801.4534139471134
Volatilidad escenario sin cobertura: 180.22223534598183
Precio más probable con cobertura: [3855.67584143]
Volatilidad escenario con cobertura: 93.31287683512937