Árboles de decisión#

Los árboles de decisión son un método de Machine Learning utilizado tanto para clasificación como para regresión. Estos algoritmos son capaces de ajustar conjuntos de datos complejos y se caracterizan por su capacidad de generar modelos fáciles de interpretar y visualizar.

Conceptos clave:

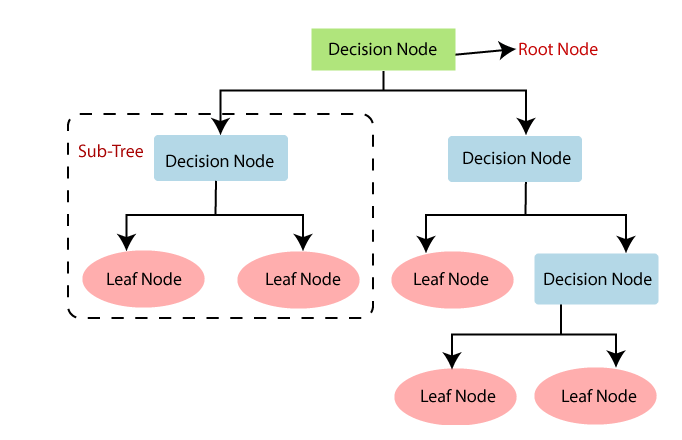
  • Nodo raíz: El nodo superior del árbol que contiene toda la población de datos. Desde aquí se inician las divisiones.

  • Nodos internos: Representan decisiones basadas en el valor de ciertos atributos.

  • Hojas: Representan la salida del modelo (clase en clasificación o valor en regresión).

  • Ramas: Conectan nodos y representan el resultado de una prueba aplicada en un nodo.

Construcción del Árbol:

La construcción de un árbol de decisión implica los siguientes pasos:

  • Selección de la característica de división: Se selecciona la característica que mejor divide el conjunto de datos utilizando criterios como el índice de Gini, la entropía o la ganancia de información.

  • División del nodo: Dividir el nodo actual en dos o más subconjuntos basados en el valor de la característica seleccionada.

  • Repetición: Repetir el proceso de selección de características y división hasta que se cumpla un criterio de parada, como alcanzar una profundidad máxima o un número mínimo de muestras en un nodo.

Ventajas:

  • Interpretabilidad: Son fáciles de entender y visualizar.

  • Preparación mínima de datos: No requieren escalado o centrado de características.

  • Flexibilidad: Pueden manejar tanto variables categóricas como numéricas.

Desventajas:

  • Sobreajuste: Tienden a sobreajustar los datos de entrenamiento si no se podan adecuadamente.

  • Inestabilidad: Pequeñas variaciones en los datos pueden producir árboles completamente diferentes.

  • Sesgo en características categóricas con muchos niveles: Pueden preferir características con muchos niveles, lo que puede llevar a divisiones menos significativas.

DecisionTree

DecisionTree#

DecisionTree-Ejemplo

DecisionTree-Ejemplo#

Metodología:#

Los árboles de decisión para clasificación realizan la clasificación en dos o más variables discretas. La metodología de los árboles de clasificación se basa en dividir el espacio de las variables de entrada con el objetivo de separarlo en regiones de elementos que pertenecen a una clase particular. Este proceso es recursivo y el árbol crece a medida que se realizan más particiones, lo que se llama profundidad.

Medidas de Impureza:

1. Impureza de Gini: Mide la probabilidad de que un elemento seleccionado al azar sea clasificado incorrectamente. La impureza de Gini se calcula como:

\[G_i = 1- \sum_{k=1}^n{p_{i,k}^2}\]

Donde \(p_{i,k}\) es la proporción de elementos de la clase k entre los elementos en el nodo i.

  • Gini < 0,1: Excelente. El nodo es casi puro.

  • Gini entre 0,1 y 0,3: Bueno. El nodo tiene una pureza razonablemente alta.

  • Gini entre 0,3 y 0,4: Aceptable. El nodo tiene cierta impureza, pero aún puede ser útil.

  • Gini > 0,4: Pobre. El nodo es bastante impuro y podría no ser muy útil para la clasificación.

Valor máximo del índice de Gini:

El valor máximo del índice de Gini depende del número de clases presentes en el nodo:

  • Para clasificación binaria (dos clases): El valor máximo del índice de Gini es 0,5. Esto ocurre cuando las dos clases están distribuidas equitativamente en el nodo, es decir, cuando \(𝑝_1=𝑝_2=0,5\)

  • Para múltiples clases (más de dos clases): El valor máximo del índice de Gini es \(1-\frac{1}{n}\), \(n\) donde es el número de clases. Esto ocurre cuando todas las clases están distribuidas equitativamente en el nodo, es decir, cuando \(𝑝_𝑖=\frac{1}{n}\) para cada clase \(𝑖\).

2. Entropía: Mide la cantidad de aleatoriedad o incertidumbre en los datos. La entropía se calcula como:

\[H_i = -\sum_{k=1}^n{p_{i,k}log_2\left(p_{i,k}\right)}\]

El objetivo es reducir la entropía después de la división, lo que se lleva a nodos más puros.

Poda (Pruning):

Para evitar el sobreajuste, se utiliza la poda:

Pre-Poda: Detener el crecimiento del árbol antes de que se torne complejo mediante la limitación de la profundidad máxima o el número mínimo de muestras en un nodo.

La pre-poda implica limitar el crecimiento del árbol durante su construcción para evitar que se torne demasiado complejo y sobreajuste los datos de entrenamiento. En scikit-learn, esto se puede lograr ajustando ciertos hiperparámetros al crear el modelo del árbol de decisión. A continuación, se presentan algunos de los hiperparámetros clave y cómo configurarlos:

  • max_depth: Limita la profundidad máxima del árbol.

  • min_samples_split: Número mínimo de muestras necesarias para dividir un nodo.

  • min_samples_leaf: Número mínimo de muestras que debe contener un nodo hoja.

  • max_leaf_nodes: Número máximo de nodos hoja.

Optimización de Hiperparámetros:#

Para evitar el sobreajuste, se deben ajustar los hiperparámetros del modelo. Los más importantes son:

  • criterion: Medida de calidad del clasificador (gini o entropy). Por defecto gini.

  • splitter: Estrategia para la división en cada nodo (best o random). Por defecto best.

  • max_depth: Profundidad máxima del árbol. Por defecto None.

  • min_samples_split: Número mínimo de muestras requeridas para dividir un nodo. Por defecto 2.

  • min_samples_leaf: Número mínimo de muestras requeridas para estar en un nodo hoja. Por defecto 1.

  • max_leaf_nodes: Número máximo de nodos hoja. Por defecto None.

Efecto de cambiar los hiperparámetros:#

En los árboles de decisión, ajustar los hiperparámetros es crucial para controlar la complejidad del modelo y prevenir el sobreajuste.

max_depth

Define la profundidad máxima del árbol.

  • Efecto de aumentar: Permite que el árbol crezca más y capture más detalles de los datos de entrenamiento, lo que puede llevar a un sobreajuste (el árbol se ajusta demasiado a los datos de entrenamiento y puede no generalizar bien en datos nuevos).

  • Efecto de disminuir: Limita la complejidad del modelo, lo que puede ayudar a evitar el sobreajuste pero puede resultar en un modelo que no captura suficiente información de los datos (subajuste).

min_samples_split

Número mínimo de muestras requeridas para dividir un nodo.

  • Efecto de aumentar: Aumenta la cantidad de muestras necesarias para realizar una división, lo que puede llevar a árboles más simples y menos profundos, ayudando a prevenir el sobreajuste.

  • Efecto de disminuir: Reduce el número de muestras necesarias para dividir un nodo, lo que puede llevar a árboles más complejos y profundos, aumentando el riesgo de sobreajuste.

min_samples_leaf

Número mínimo de muestras que debe contener un nodo hoja.

  • Efecto de aumentar: Asegura que los nodos hoja contengan un mayor número de muestras, lo que puede suavizar el modelo y prevenir el sobreajuste, pero también puede hacer que el modelo pierda detalles importantes.

  • Efecto de disminuir: Permite nodos hoja con menos muestras, lo que puede hacer el modelo más detallado pero también más susceptible al sobreajuste.

max_leaf_nodes

Número máximo de nodos hoja en el árbol.

  • Efecto de aumentar: Permite más nodos hoja, lo que puede hacer el modelo más complejo y preciso, pero también aumenta el riesgo de sobreajuste.

  • Efecto de disminuir: Limita el número de nodos hoja, simplificando el modelo y ayudando a prevenir el sobreajuste, pero puede hacer que el modelo pierda detalles y subajuste.

splitter

Estrategia utilizada para dividir en cada nodo. Las opciones comunes son best y random.

  • Efecto de usar best: Selecciona la mejor división posible basada en el criterio de impureza. Tiende a producir árboles más precisos, pero puede ser más lento.

  • Efecto de usar random: Selecciona la mejor división entre un subconjunto aleatorio de características. Puede hacer el modelo más rápido y a veces puede ayudar a prevenir el sobreajuste al introducir variabilidad.