Comparación de modelos precio de electricidad#
Métricas de desempeño#
Raíz del Error Cuadrático Medio (RMSE)
Mide la magnitud promedio del error cuadrático entre los valores observados y los valores predichos. Penaliza fuertemente los errores grandes.
Error Porcentual Absoluto Medio (MAPE)
Indica el error promedio en términos porcentuales. Es útil para interpretar el error relativo con respecto al valor real.
Error Máximo (Max Error)
Representa la mayor desviación absoluta entre las predicciones y los valores reales. Evalúa el peor caso de error del modelo.
Coeficiente de Determinación Ajustado (R² ajustado)
Evalúa qué tan bien el modelo explica la variabilidad de los datos, ajustando por el número de parámetros estimados. A diferencia del R² tradicional, penaliza la complejidad excesiva del modelo.
donde:
\(n\) es el número de observaciones y \(k\) el número de parámetros estimados en el modelo.
Rangos sugeridos de calidad del ajuste
R² ajustado (escala 0–1)
Categoría |
Rango |
|---|---|
Excelente |
\(R^2_{ajustado} \ge 0{,}90\) |
Bueno |
\(0{,}75 \le R^2_{ajustado} < 0{,}90\) |
Moderado / Aceptable |
\(0{,}50 \le R^2_{ajustado} < 0{,}75\) |
Deficiente |
\(R^2_{ajustado} < 0{,}50\) |
MAPE (porcentaje)
Categoría |
Rango |
|---|---|
Excelente |
\(MAPE < 10\%\) |
Bueno |
\(10\% \le MAPE < 20\%\) |
Moderado / Aceptable |
\(20\% \le MAPE < 50\%\) |
Deficiente |
\(MAPE \ge 50\%\) |
Estas categorías permiten interpretar de manera cualitativa la capacidad predictiva del modelo.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from scipy.stats import boxcox
from statsmodels.tsa.statespace.sarimax import SARIMAX
import statsmodels.api as sm
from scipy.stats import norm
Funciones#
Nueva función evaluar_metricas_desempeno
def plot_serie_tiempo(
serie: pd.DataFrame,
nombre: str,
unidades: str = None,
columna: str = None,
fecha_inicio: str = None,
fecha_fin: str = None,
color: str = 'navy',
linewidth: float = 2,
num_xticks: int = 12,
estacionalidad: str = None, # 'diciembre', 'enero', 'semana', 'semestre', 'custom_month'
custom_month: int = None, # Si quieres marcar otro mes (ejemplo: 3 para marzo)
vline_label: str = None, # Etiqueta para la(s) línea(s) vertical(es)
hlines: list = None, # lista de valores horizontales a marcar
hlines_labels: list = None, # lista de etiquetas para líneas horizontales
color_estacion: str = 'darkgray', # color de las líneas estacionales
alpha_estacion: float = 0.3, # transparencia de líneas estacionales
color_hline: str = 'gray', # color de las líneas horizontales
alpha_hline: float = 0.7 # transparencia de líneas horizontales
):
"""
Gráfico elegante de serie de tiempo.
- Eje X alineado con la primera fecha real de la serie.
- Opcional: marcar estacionalidades (diciembres, semanas, semestres, mes personalizado) con etiqueta.
- Líneas horizontales con etiqueta opcional (legend).
"""
df = serie.copy()
if columna is None:
columna = df.columns[0]
if fecha_inicio:
df = df[df.index >= fecha_inicio]
if fecha_fin:
df = df[df.index <= fecha_fin]
# Asegura que el índice sea datetime y esté ordenado
df = df.sort_index()
df.index = pd.to_datetime(df.index)
plt.style.use('ggplot')
fig, ax = plt.subplots(figsize=(14, 6))
# Gráfica principal
ax.plot(df.index, df[columna], color=color, linewidth=linewidth, label=nombre)
ax.set_title(f"Serie de tiempo: {nombre}", fontsize=20, weight='bold',
color='black')
ax.set_xlabel("Fecha", fontsize=15, color='black')
ax.set_ylabel(unidades, fontsize=15, color='black')
ax.tick_params(axis='both', colors='black', labelsize=13)
for label in ax.get_xticklabels() + ax.get_yticklabels():
label.set_color('black')
# Limita el rango del eje X exactamente al rango de fechas de la serie (no corrido)
ax.set_xlim(df.index.min(), df.index.max())
# Ticks equidistantes en eje X, asegurando que empieza en la primera fecha
idx = df.index
if len(idx) > num_xticks:
ticks = np.linspace(0, len(idx)-1, num_xticks, dtype=int)
ticks[0] = 0 # asegúrate que arranque en la primera fecha
ticklabels = [idx[i] for i in ticks]
ax.set_xticks(ticklabels)
ax.set_xticklabels([pd.to_datetime(t).strftime('%b %Y') for t in ticklabels], rotation=0, color='black')
else:
ax.xaxis.set_major_formatter(mdates.DateFormatter('%b %Y'))
fig.autofmt_xdate(rotation=0)
# ==============================
# LÍNEAS VERTICALES: Estacionalidad (con etiqueta en leyenda si se desea)
# ==============================
vlines_plotted = False
if estacionalidad is not None:
if estacionalidad == 'diciembre':
fechas_mark = df[df.index.month == 12].index
elif estacionalidad == 'enero':
fechas_mark = df[df.index.month == 1].index
elif estacionalidad == 'semana':
fechas_mark = df[df.index.weekday == 0].index
elif estacionalidad == 'semestre':
fechas_mark = df[df.index.month.isin([6, 12])].index
elif estacionalidad == 'custom_month' and custom_month is not None:
fechas_mark = df[df.index.month == custom_month].index
else:
fechas_mark = []
for i, f in enumerate(fechas_mark):
# Solo pone la etiqueta una vez (la primera línea)
if not vlines_plotted and vline_label is not None:
ax.axvline(f, color=color_estacion, alpha=alpha_estacion, linewidth=2, linestyle='--', zorder=0, label=vline_label)
vlines_plotted = True
else:
ax.axvline(f, color=color_estacion, alpha=alpha_estacion, linewidth=2, linestyle='--', zorder=0)
# ==============================
# LÍNEAS HORIZONTALES OPCIONALES, con leyenda
# ==============================
if hlines is not None:
if hlines_labels is None:
hlines_labels = [None] * len(hlines)
for i, h in enumerate(hlines):
if hlines_labels[i] is not None:
ax.axhline(h, color=color_hline, alpha=alpha_hline, linewidth=1.5, linestyle='--', zorder=0, label=hlines_labels[i])
else:
ax.axhline(h, color=color_hline, alpha=alpha_hline, linewidth=1.5, linestyle='--', zorder=0)
# Coloca la leyenda solo si hay etiquetas
handles, labels = ax.get_legend_handles_labels()
if any(labels):
ax.legend(loc='best', fontsize=13, frameon=True)
ax.grid(True, alpha=0.4)
plt.tight_layout()
plt.show()
##################################################################################
def analisis_estacionariedad_full(
serie: pd.Series,
nombre: str = None,
lags: int = 24,
xtick_interval: int = 3
):
"""
Gráfica y análisis de estacionariedad para una serie de tiempo con múltiples transformaciones:
- Serie original
- Diferenciación
- Logaritmo
- Diferenciación del Logaritmo
- Raíz cuadrada
- Diferenciación de la raíz cuadrada
- Box-Cox (con corrimiento si hay valores <= 0)
- Diferenciación del Box-Cox
Para cada transformación se grafica:
- Serie transformada en el tiempo
- ACF
- PACF
- Resultado de la prueba ADF con interpretación
Args:
serie: Serie de tiempo (índice datetime, pandas.Series)
nombre: Nombre de la serie (para títulos)
lags: Número de rezagos para ACF/PACF
xtick_interval: Mostrar ticks en X cada este número de lags, incluyendo siempre el lag 1
Return:
dict con los resultados de la ADF para cada transformación
"""
if nombre is None:
nombre = serie.name if serie.name is not None else "Serie"
serie = serie.astype(float).copy()
serie_orig = serie.copy()
serie_diff = serie_orig.diff().dropna()
# Logaritmo
if (serie_orig <= 0).any():
log_ok = False
serie_log = pd.Series([np.nan]*len(serie_orig), index=serie_orig.index)
serie_log_diff = pd.Series([np.nan]*len(serie_orig), index=serie_orig.index)
else:
log_ok = True
serie_log = np.log(serie_orig)
serie_log_diff = serie_log.diff().dropna()
# Raíz cuadrada
if (serie_orig < 0).any():
sqrt_ok = False
serie_sqrt = pd.Series([np.nan]*len(serie_orig), index=serie_orig.index)
serie_sqrt_diff = pd.Series([np.nan]*len(serie_orig), index=serie_orig.index)
else:
sqrt_ok = True
serie_sqrt = np.sqrt(serie_orig)
serie_sqrt_diff = serie_sqrt.diff().dropna()
# Box–Cox
if (serie_orig <= 0).any():
shift_bc = 1 - serie_orig.min()
else:
shift_bc = 0.0
serie_bc_input = serie_orig + shift_bc
if (serie_bc_input <= 0).any():
bc_ok = False
serie_boxcox = pd.Series([np.nan]*len(serie_orig), index=serie_orig.index)
serie_boxcox_diff = pd.Series([np.nan]*len(serie_orig), index=serie_orig.index)
lambda_bc = np.nan
else:
bc_ok = True
bc_vals, lambda_bc = boxcox(serie_bc_input.values)
serie_boxcox = pd.Series(bc_vals, index=serie_orig.index)
serie_boxcox_diff = serie_boxcox.diff().dropna()
# --- Títulos actualizados ---
titulos = [
f"Serie original: {nombre}",
"Diferenciación",
"Logaritmo" + ("" if log_ok else " (no aplicable)"),
"Diferenciación del Logaritmo" + ("" if log_ok else " (no aplicable)"),
"Raíz cuadrada" + ("" if sqrt_ok else " (no aplicable)"),
"Diferenciación de la raíz cuadrada" + ("" if sqrt_ok else " (no aplicable)"),
"Box-Cox" + (f" (λ = {lambda_bc:.4f})" if bc_ok else " (no aplicable)"),
"Diferenciación del Box-Cox" + ("" if bc_ok else " (no aplicable)")
]
series = [
serie_orig,
serie_diff,
serie_log,
serie_log_diff,
serie_sqrt,
serie_sqrt_diff,
serie_boxcox,
serie_boxcox_diff
]
# --- ADF ---
resultados_adf = []
interpretaciones = []
for i, s in enumerate(series):
s_ = s.dropna()
if len(s_) < 5:
resultados_adf.append((np.nan, np.nan))
interpretaciones.append("No evaluable")
continue
regression_type = 'ct' if i in [0, 2, 4, 6] else 'c'
try:
adf_res = adfuller(s_, regression=regression_type, autolag='AIC')
estadistico = adf_res[0]
pvalue = adf_res[1]
except Exception:
estadistico = np.nan
pvalue = np.nan
resultados_adf.append((estadistico, pvalue))
interpretaciones.append("Estacionaria" if (pvalue is not None and pvalue < 0.05) else "No estacionaria")
# --- Gráficos ---
filas = len(series)
fig, axes = plt.subplots(filas, 3, figsize=(18, 4*filas), squeeze=False)
colores = ['black'] * filas
for fila in range(filas):
serie_fila = series[fila]
# Serie temporal
axes[fila, 0].plot(serie_fila, color=colores[fila], lw=1)
axes[fila, 0].set_title(titulos[fila], color='black')
axes[fila, 0].set_xlabel("Fecha", color='black')
if fila == 0:
ylabel = "Valor"
elif fila == 1:
ylabel = "Δ Valor"
elif fila == 2:
ylabel = "Log(Valor)"
elif fila == 3:
ylabel = "Δ Log(Valor)"
elif fila == 4:
ylabel = "√Valor"
elif fila == 5:
ylabel = "Δ √Valor"
elif fila == 6:
ylabel = "Box-Cox"
else:
ylabel = "Δ Box-Cox"
axes[fila, 0].set_ylabel(ylabel, color='black')
axes[fila, 0].grid(True, alpha=0.3)
axes[fila, 0].tick_params(axis='both', labelsize=11, colors='black')
adf_est, adf_p = resultados_adf[fila]
axes[fila, 0].text(
0.02, 0.85,
f"ADF: {adf_est:.2f}\np-valor: {adf_p:.4f}\n{interpretaciones[fila]}",
transform=axes[fila, 0].transAxes,
fontsize=11,
bbox=dict(facecolor='white', alpha=0.85),
color='black'
)
# ACF
try:
plot_acf(serie_fila.dropna(), lags=lags, ax=axes[fila, 1], zero=False, color=colores[fila])
except Exception:
axes[fila, 1].text(0.5, 0.5, "ACF no disponible", ha='center', va='center')
axes[fila, 1].set_title("ACF", color='black')
xticks = [1] + list(range(xtick_interval, lags + 1, xtick_interval))
axes[fila, 1].set_xticks(sorted(set(xticks)))
axes[fila, 1].tick_params(axis='both', labelsize=11, colors='black')
axes[fila, 1].set_xlabel("Lag", color='black')
# PACF
try:
plot_pacf(serie_fila.dropna(), lags=lags, ax=axes[fila, 2], zero=False, color=colores[fila])
except Exception:
axes[fila, 2].text(0.5, 0.5, "PACF no disponible", ha='center', va='center')
axes[fila, 2].set_title("PACF", color='black')
axes[fila, 2].set_xticks(sorted(set(xticks)))
axes[fila, 2].tick_params(axis='both', labelsize=11, colors='black')
axes[fila, 2].set_xlabel("Lag", color='black')
plt.tight_layout()
plt.show()
# --- Resumen ADF ---
adf_dict = {
titulos[i]: {
"estadístico ADF": resultados_adf[i][0],
"p-valor": resultados_adf[i][1],
"interpretación": interpretaciones[i],
"nota_boxcox": (
f"lambda Box-Cox = {lambda_bc:.4f}, shift aplicado = {shift_bc:.4f}"
if ("Box-Cox" in titulos[i] and bc_ok)
else ("Box-Cox no aplicable" if "Box-Cox" in titulos[i] and not bc_ok else None)
)
}
for i in range(filas)
}
return adf_dict
##################################################################################
def analisis_residuales(
residuals,
nombre: str = "Serie de tiempo",
lags: int = 24,
color_resid: str = "navy",
color_qq: str = "navy",
color_acf_pacf: str = "navy"
):
"""
Análisis gráfico de residuales:
- Residuales en el tiempo (toda la fila superior)
- Histograma + curva normal (izq), QQ-plot (der)
- ACF (izq), PACF (der) con bandas y barras color navy
"""
residuals = residuals[1:].dropna()
mu = residuals.mean()
sigma = residuals.std(ddof=1)
x = np.linspace(residuals.min(), residuals.max(), 400)
pdf = norm.pdf(x, loc=mu, scale=sigma)
fig = plt.figure(constrained_layout=True, figsize=(14, 11))
gs = fig.add_gridspec(3, 2, height_ratios=[1, 1, 1])
# 1. Residuales en el tiempo
ax_time = fig.add_subplot(gs[0, :])
ax_time.scatter(residuals.index, residuals, color=color_resid, alpha=0.7, s=20)
ax_time.axhline(0, ls="--", color="black")
ax_time.set_title(f"Residuales en el tiempo: {nombre}", color='black')
ax_time.set_xlabel("Tiempo", color='black')
ax_time.set_ylabel("Residual", color='black')
ax_time.tick_params(axis='both', labelsize=11, colors='black')
# 2. Histograma + curva Normal
ax_hist = fig.add_subplot(gs[1, 0])
ax_hist.hist(residuals, bins="auto", density=True, alpha=0.6, edgecolor="k", color="royalblue")
ax_hist.plot(x, pdf, lw=2, label=f"N({mu:.3f}, {sigma:.3f}²)", color="darkred")
ax_hist.set_title("Histograma residuaes y ajuste Normal", color='black')
ax_hist.set_xlabel("Residual", color='black')
ax_hist.set_ylabel("Densidad", color='black')
ax_hist.legend(fontsize=9)
ax_hist.grid(alpha=0.18)
ax_hist.tick_params(axis='both', labelsize=10, colors='black')
# 3. QQ-plot
ax_qq = fig.add_subplot(gs[1, 1])
qq = sm.qqplot(residuals, line='45', fit=True, ax=ax_qq, markerfacecolor=color_qq, markeredgecolor=color_qq, marker='o')
lines = ax_qq.get_lines()
if len(lines) >= 1:
lines[0].set_color(color_qq)
lines[0].set_marker('o')
lines[0].set_linestyle('None')
if len(lines) >= 2:
lines[1].set_color("black")
lines[1].set_linestyle("--")
ax_qq.set_title("Q-Q Plot de los residuales", color='black')
ax_qq.set_xlabel("Cuantiles teóricos (Normal)", color='black')
ax_qq.set_ylabel("Cuantiles de los residuales", color='black')
ax_qq.tick_params(axis='both', labelsize=10, colors='black')
for l in ax_qq.get_xticklabels() + ax_qq.get_yticklabels():
l.set_color('black')
# 4. ACF (usando color navy en barras y bandas)
ax_acf = fig.add_subplot(gs[2, 0])
sm.graphics.tsa.plot_acf(residuals, lags=lags, ax=ax_acf, zero=False, color=color_acf_pacf)
ax_acf.set_title("ACF de los residuales", color='black')
ax_acf.set_xlabel("Rezagos", color='black')
ax_acf.set_ylabel("Autocorrelación", color='black')
ax_acf.tick_params(axis='both', labelsize=10, colors='black')
# 5. PACF (usando color navy en barras y bandas)
ax_pacf = fig.add_subplot(gs[2, 1])
sm.graphics.tsa.plot_pacf(residuals, lags=lags, ax=ax_pacf, zero=False, color=color_acf_pacf)
ax_pacf.set_title("PACF de los residuales", color='black')
ax_pacf.set_xlabel("Rezagos", color='black')
ax_pacf.set_ylabel("Autocorrelación parcial", color='black')
ax_pacf.tick_params(axis='both', labelsize=10, colors='black')
plt.show()
return
##################################################################################
def analizar_ajuste_serie(
serie_original,
fitted_values,
results,
test,
n_forecast,
transformacion=None, # 'log', 'boxcox', 'sqrt', o None
lambda_bc=None, # solo si boxcox
nombre="Serie"
):
"""
Analiza el ajuste de un modelo y grafica ajuste+pronóstico sobre la serie original,
devolviendo predicciones revertidas a la escala original.
Args:
serie_original: Serie original (sin transformar, index datetime)
fitted_values: Serie de fittedvalues (en escala transformada)
results: Modelo ajustado de statsmodels (debe soportar .append, .get_forecast)
test: Serie de test (index datetime)
n_forecast: Períodos a pronosticar por fuera de la muestra
transformacion: 'log', 'boxcox', 'sqrt' o None
lambda_bc: Valor de lambda para boxcox (si aplica)
nombre: Nombre para los ejes y leyenda
Returns:
Diccionario con:
- y_pred_train, y_pred_test, forecasting_orig, lower_bt, upper_bt
- Fechas de pronóstico futuro: future_dates
"""
# Alinear índices por seguridad
fitted_values = fitted_values.reindex(serie_original.index.intersection(fitted_values.index))
test = test.copy()
# ----------- PRONÓSTICO EN TEST (fuera de muestra, recursivo) -----------
current_results = results
forecasted_test = []
lower_ci_test = []
upper_ci_test = []
for i in range(len(test)):
forecaster = current_results.get_forecast(steps=1)
forecast_mean_test = forecaster.predicted_mean.iloc[0]
ci_i_test = forecaster.conf_int(alpha=0.05).iloc[0]
forecasted_test.append(forecast_mean_test)
lower_ci_test.append(ci_i_test.iloc[0])
upper_ci_test.append(ci_i_test.iloc[1])
# Recursivo: alimentar el modelo con el valor real observado
current_results = current_results.append(endog=[test.iloc[i]], refit=False)
forecasted_test = pd.Series(forecasted_test, index=test.index, name='forecast_test')
lower_ci_test = pd.Series(lower_ci_test, index=test.index, name='lower_test')
upper_ci_test = pd.Series(upper_ci_test, index=test.index, name='upper_test')
# ----------- PRONÓSTICO FUTURO (n_forecast meses) -----------
current_results = results.append(endog=test, refit=False)
forecasting = []
lower_ci = []
upper_ci = []
for i in range(n_forecast):
forecaster = current_results.get_forecast(steps=1)
forecast_mean = forecaster.predicted_mean.iloc[0]
ci_i = forecaster.conf_int(alpha=0.05).iloc[0]
forecasting.append(forecast_mean)
lower_ci.append(ci_i.iloc[0])
upper_ci.append(ci_i.iloc[1])
current_results = current_results.append(endog=[forecast_mean], refit=False)
# Fechas futuras mensuales (puedes personalizar)
last_date = test.index[-1]
future_dates = pd.date_range(start=last_date + pd.offsets.MonthBegin(1),
periods=n_forecast, freq='MS')
forecasting = pd.Series(forecasting, index=future_dates, name='forecast')
lower_ci = pd.Series(lower_ci, index=future_dates, name='lower')
upper_ci = pd.Series(upper_ci, index=future_dates, name='upper')
# ----------- REVERSIÓN DE TRANSFORMACIÓN -----------
if transformacion == "log":
y_pred_train = np.exp(fitted_values)
y_pred_test = np.exp(forecasted_test)
forecasting_orig = np.exp(forecasting)
lower_bt = np.exp(lower_ci)
upper_bt = np.exp(upper_ci)
elif transformacion == "boxcox":
if lambda_bc is None:
raise ValueError("Debes indicar lambda_bc para la transformación Box-Cox")
y_pred_train = np.power((lambda_bc * fitted_values + 1), 1 / lambda_bc)
y_pred_test = np.power((lambda_bc * forecasted_test + 1), 1 / lambda_bc)
forecasting_orig = np.power((lambda_bc * forecasting + 1), 1 / lambda_bc)
lower_bt = np.power((lambda_bc * lower_ci + 1), 1 / lambda_bc)
upper_bt = np.power((lambda_bc * upper_ci + 1), 1 / lambda_bc)
elif transformacion == "sqrt":
y_pred_train = fitted_values ** 2
y_pred_test = forecasted_test ** 2
forecasting_orig = forecasting ** 2
lower_bt = lower_ci ** 2
upper_bt = upper_ci ** 2
elif transformacion is None or transformacion == "none":
y_pred_train = fitted_values
y_pred_test = forecasted_test
forecasting_orig = forecasting
lower_bt = lower_ci
upper_bt = upper_ci
else:
raise ValueError("Transformación no soportada. Usa 'log', 'boxcox', 'sqrt' o None.")
# ----------- GRÁFICO -----------
plt.figure(figsize=(12,6))
# Serie original
plt.plot(serie_original, label=nombre, color='black')
# Ajuste en train
plt.plot(y_pred_train, label='Ajuste en train', color='tab:blue')
# Ajuste en test
plt.plot(y_pred_test, label='Pronóstico en test', color='tab:green')
# Pronóstico futuro + IC
plt.plot(forecasting_orig, label='Pronóstico futuro', color='tab:red', linestyle='--')
plt.fill_between(future_dates, lower_bt.values, upper_bt.values, color='tab:red', alpha=0.2, label='IC 95%')
plt.title(f'Ajuste y pronóstico - {nombre}')
plt.xlabel('Tiempo')
plt.ylabel('Valor')
plt.legend()
plt.tight_layout()
plt.show()
# ----------- Devuelve resultados clave -----------
return {
'y_pred_train': y_pred_train,
'y_pred_test': y_pred_test,
'forecasting_orig': forecasting_orig,
'lower_bt': lower_bt,
'upper_bt': upper_bt,
'future_dates': future_dates
}
##################################################################################
def _inverse_transform(y, transformacion=None, lambda_bc=None):
"""Revierte la transformación aplicada a una Serie o arreglo."""
if y is None:
return None
y_vals = y.values if isinstance(y, (pd.Series, pd.Index)) else np.asarray(y)
if transformacion is None or str(transformacion).lower() in ("none", ""):
inv = y_vals
elif str(transformacion).lower() == "log":
inv = np.exp(y_vals)
elif str(transformacion).lower() == "sqrt":
inv = np.power(y_vals, 2)
elif str(transformacion).lower() == "boxcox":
if lambda_bc is None:
raise ValueError("Para 'boxcox' debes proporcionar lambda_bc.")
inv = np.power((lambda_bc * y_vals + 1.0), 1.0 / lambda_bc)
else:
raise ValueError("Transformación no soportada. Usa 'log', 'boxcox', 'sqrt' o None.")
if isinstance(y, pd.Series):
return pd.Series(inv, index=y.index, name=y.name)
else:
return inv
def _recursive_forecast_over_test(results, test):
"""Pronóstico recursivo 1-paso-ahead sobre TEST."""
current_results = results
preds, lowers, uppers = [], [], []
for i in range(len(test)):
forecaster = current_results.get_forecast(steps=1)
mean_i = forecaster.predicted_mean.iloc[0]
ci_i = forecaster.conf_int(alpha=0.05).iloc[0]
preds.append(mean_i)
lowers.append(ci_i.iloc[0])
uppers.append(ci_i.iloc[1])
# Se alimenta el valor real observado
current_results = current_results.append(endog=[test.iloc[i]], refit=False)
y_pred_test = pd.Series(preds, index=test.index, name="forecast_test")
lower_ci = pd.Series(lowers, index=test.index, name="lower_test")
upper_ci = pd.Series(uppers, index=test.index, name="upper_test")
return y_pred_test, lower_ci, upper_ci
def _ajustado(r2, n, p):
"""Calcula el R² ajustado."""
if n - p - 1 <= 0:
return np.nan
return 1 - (1 - r2) * (n - 1) / (n - p - 1)
def evaluar_metricas_desempeno(
train,
test,
results,
transformacion=None, # 'log', 'boxcox', 'sqrt' o None
lambda_bc=None, # solo si boxcox
nombre="Precio de electricidad",
imprimir=True
):
"""
Calcula las métricas (R², R² ajustado, RMSE, MAPE, Max Error)
para TRAIN y TEST en la escala original, usando sklearn.
"""
# 1) Fitted values en escala transformada
fitted_transf = results.fittedvalues
fitted_transf = fitted_transf.reindex(train.index)
# 2) Pronóstico recursivo en TEST
y_pred_test_transf, lower_ci_transf, upper_ci_transf = _recursive_forecast_over_test(results, test)
# 3) Revertir transformaciones
y_train_orig = _inverse_transform(train, transformacion, lambda_bc)
y_test_orig = _inverse_transform(test, transformacion, lambda_bc)
y_pred_train_orig = _inverse_transform(fitted_transf, transformacion, lambda_bc)
y_pred_test_orig = _inverse_transform(y_pred_test_transf, transformacion, lambda_bc)
lower_test_orig = _inverse_transform(lower_ci_transf, transformacion, lambda_bc)
upper_test_orig = _inverse_transform(upper_ci_transf, transformacion, lambda_bc)
# 4) Extraer cantidad de parámetros (para R² ajustado)
try:
p_eff = int(getattr(results, "k_params", 1))
except Exception:
p_eff = 1
# 5) Cálculo de métricas con sklearn
n_train = len(y_train_orig)
n_test = len(y_test_orig)
r2_train = r2_score(y_train_orig, y_pred_train_orig)
rmse_train = np.sqrt(mean_squared_error(y_train_orig, y_pred_train_orig))
mape_train = mean_absolute_percentage_error(y_train_orig, y_pred_train_orig) * 100
maxerr_train = max_error(y_train_orig, y_pred_train_orig)
r2adj_train = _ajustado(r2_train, n_train, p_eff)
r2_test = r2_score(y_test_orig, y_pred_test_orig)
rmse_test = np.sqrt(mean_squared_error(y_test_orig, y_pred_test_orig))
mape_test = mean_absolute_percentage_error(y_test_orig, y_pred_test_orig) * 100
maxerr_test = max_error(y_test_orig, y_pred_test_orig)
r2adj_test = _ajustado(r2_test, n_test, p_eff)
# 6) Tabla resumen
tabla = pd.DataFrame({
"Train": [rmse_train, mape_train, maxerr_train, r2_train, r2adj_train],
"Test": [rmse_test, mape_test, maxerr_test, r2_test, r2adj_test]
}, index=["RMSE", "MAPE (%)", "Max Error", "R2", "R2 Ajustado"])
if imprimir:
titulo = f"Métricas de desempeño - {nombre}"
print("\n" + titulo)
print("-" * len(titulo))
display(tabla.style.format({
"Train": "{:,.4f}",
"Test": "{:,.4f}"
}))
return {
"tabla_metricas": tabla,
"y_train_orig": y_train_orig,
"y_test_orig": y_test_orig,
"y_pred_train_orig": y_pred_train_orig,
"y_pred_test_orig": y_pred_test_orig,
"lower_test_orig": lower_test_orig,
"upper_test_orig": upper_test_orig
}
Precio de electricidad#
# Cargar el archivo
precio_electricidad = pd.read_csv("Precio_electricidad.csv")
# Corregir nombres de columnas si tienen espacios
precio_electricidad.columns = precio_electricidad.columns.str.strip()
# Convertir 'Fecha' a datetime y usar como índice
precio_electricidad['Fecha'] = pd.to_datetime(precio_electricidad['Fecha'])
precio_electricidad.set_index('Fecha', inplace=True)
# Ordenar por fecha por si acaso
precio_electricidad = precio_electricidad.sort_index()
# Establecer frecuencia explícita para evitar el warning de statsmodels
precio_electricidad.index.freq = precio_electricidad.index.inferred_freq
precio_electricidad.head()
| Precio | |
|---|---|
| Fecha | |
| 2000-01-01 | 36.539729 |
| 2000-02-01 | 39.885205 |
| 2000-03-01 | 35.568126 |
| 2000-04-01 | 44.957443 |
| 2000-05-01 | 33.848903 |
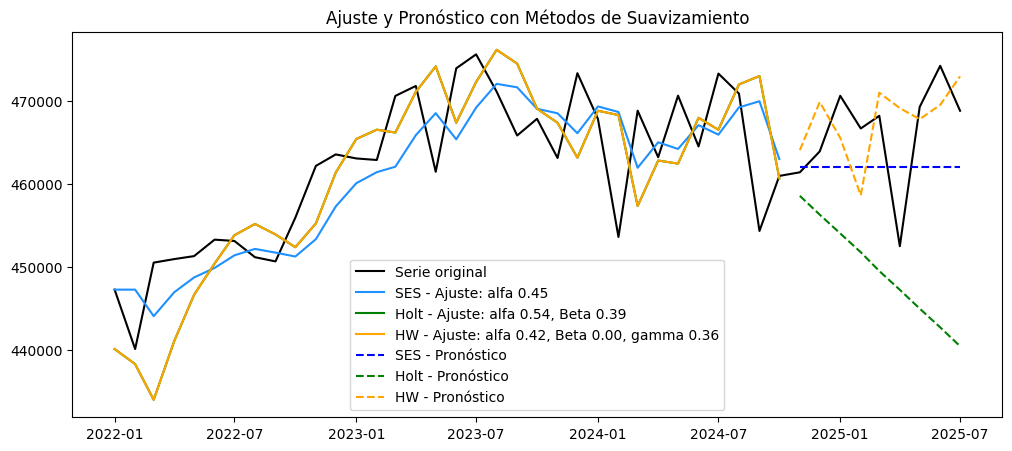
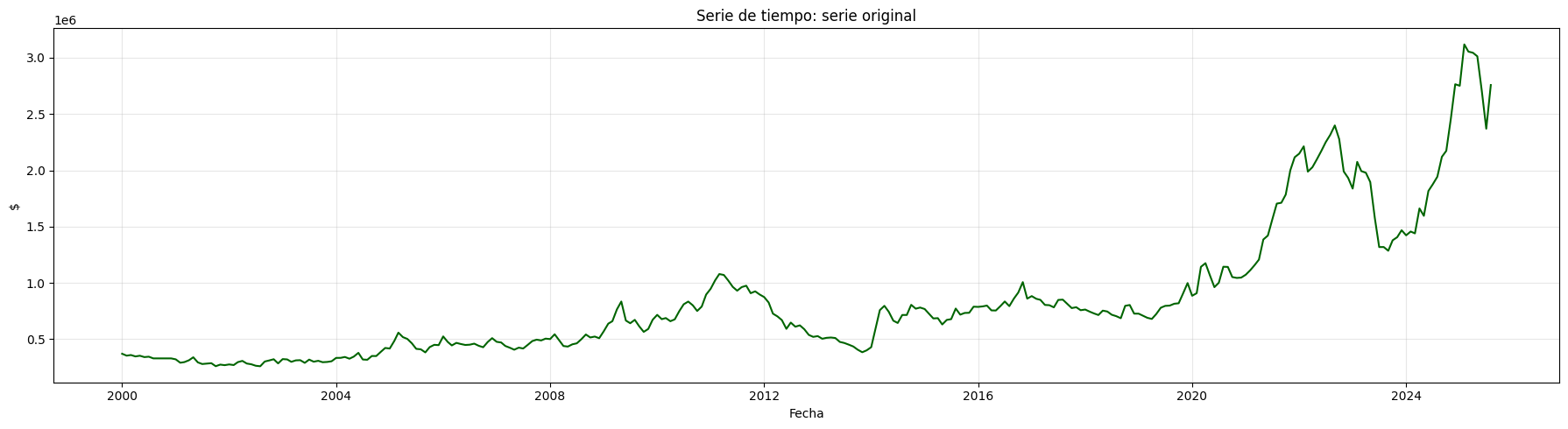
plot_serie_tiempo(
precio_electricidad,
nombre="Precio de electricidad",
columna='Precio',
unidades='COP/kWh',
estacionalidad='diciembre',
vline_label="Diciembre",
num_xticks = 14
)
adf_resultados = analisis_estacionariedad_full(
precio_electricidad['Precio'],
nombre="Precio de electricidad",
lags=36,
xtick_interval=3
)
Transformación Box–Cox#
# Aplicar la transformación Box–Cox:
y_boxcox, lambda_bc = boxcox(precio_electricidad.iloc[:, 0])
# Convertir el resultado en pandas.Series
y_boxcox = pd.DataFrame(y_boxcox, index=precio_electricidad.index, columns=['Precio_boxcox'])
print(f"Lambda Box–Cox óptimo: {lambda_bc:.4f}")
print(y_boxcox.head())
Lambda Box–Cox óptimo: -0.3692
Precio_boxcox
Fecha
2000-01-01 1.991101
2000-02-01 2.013932
2000-03-01 1.983928
2000-04-01 2.043960
2000-05-01 1.970553
Conjunto de train y test:#
# Dividir en train y test (por ejemplo, 80% train, 20% test)
split = int(len(y_boxcox) * 0.8)
train, test = y_boxcox[:split], y_boxcox[split:]
# Graficar train y test:
plt.figure(figsize=(12, 5))
plt.plot(train, label='Train', color='navy')
plt.plot(test, label='Test', color='orange')
plt.title("Conjunto de train y test")
plt.xlabel("Fecha")
plt.ylabel("Valor")
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
import itertools
from statsmodels.tsa.statespace.sarimax import SARIMAX
Silenciar solo los warning:
import warnings
from statsmodels.tools.sm_exceptions import ConvergenceWarning
warnings.filterwarnings("ignore",
message="Non-invertible starting MA parameters",
category=UserWarning)
warnings.filterwarnings("ignore",
message="Non-stationary starting autoregressive parameters",
category=UserWarning)
warnings.filterwarnings("ignore", category=ConvergenceWarning)
MA(3)#
# Definir los parámetros del modelo ARIMA (p, d, q)
order = (0, 1, 3) # Puedes ajustar según el análisis de ACF y PACF
trend = 'n' # 'c' = constante, 't' = tendencia, 'ct' = constante + tendencia, 'n' = sin tendencia
seasonal_order = (0, 0, 0, 0) # Parámetros de la estacionalidad (P, D, Q, s)
# Ajustar el modelo con los datos de entrenamiento
model = SARIMAX(train, order=order, seasonal_order=seasonal_order, trend=trend)
results = model.fit()
# Mostrar resumen del modelo
print(results.summary())
SARIMAX Results
==============================================================================
Dep. Variable: Precio_boxcox No. Observations: 232
Model: SARIMAX(0, 1, 3) Log Likelihood 403.688
Date: Mon, 24 Nov 2025 AIC -799.377
Time: 19:08:01 BIC -785.607
Sample: 01-01-2000 HQIC -793.823
- 04-01-2019
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ma.L1 -0.1016 0.060 -1.680 0.093 -0.220 0.017
ma.L2 -0.1952 0.059 -3.299 0.001 -0.311 -0.079
ma.L3 -0.1692 0.066 -2.581 0.010 -0.298 -0.041
sigma2 0.0018 0.000 11.255 0.000 0.001 0.002
===================================================================================
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 0.85
Prob(Q): 0.97 Prob(JB): 0.65
Heteroskedasticity (H): 1.58 Skew: 0.09
Prob(H) (two-sided): 0.05 Kurtosis: 3.24
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
Ajuste y pronóstico en la serie original#
fitted_values = results.fittedvalues
y_pred_train = np.power((lambda_bc * fitted_values + 1), 1 / lambda_bc)
y_pred = y_pred_train[1:]
y_real = precio_electricidad["Precio"][1:split]
resultados = analizar_ajuste_serie(
precio_electricidad, # Serie original (sin transformar)
fitted_values, # Ajuste en train
results, # Modelo ajustado
test, # Datos test
n_forecast=12, # Periodos futuros
transformacion='boxcox', # 'log', 'boxcox', 'sqrt' o None
lambda_bc=lambda_bc, # Solo si es boxcox
nombre="Precio de electricidad"
)

### Gráfico de valores predichos vs. valores reales
plt.figure(figsize=(6,6))
plt.scatter(y_real, y_pred, color='blue', alpha=0.6, edgecolor='k')
# Línea de identidad (y = x)
min_val = min(y_real.min(), y_pred.min())
max_val = max(y_real.max(), y_pred.max())
plt.plot([min_val, max_val], [min_val, max_val], color='black', lw=2)
plt.title("Valores predichos vs. valores reales", fontsize=12)
plt.xlabel("Valores reales")
plt.ylabel("Valores predichos")
plt.axis("equal") # asegura proporciones iguales para la diagonal
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()
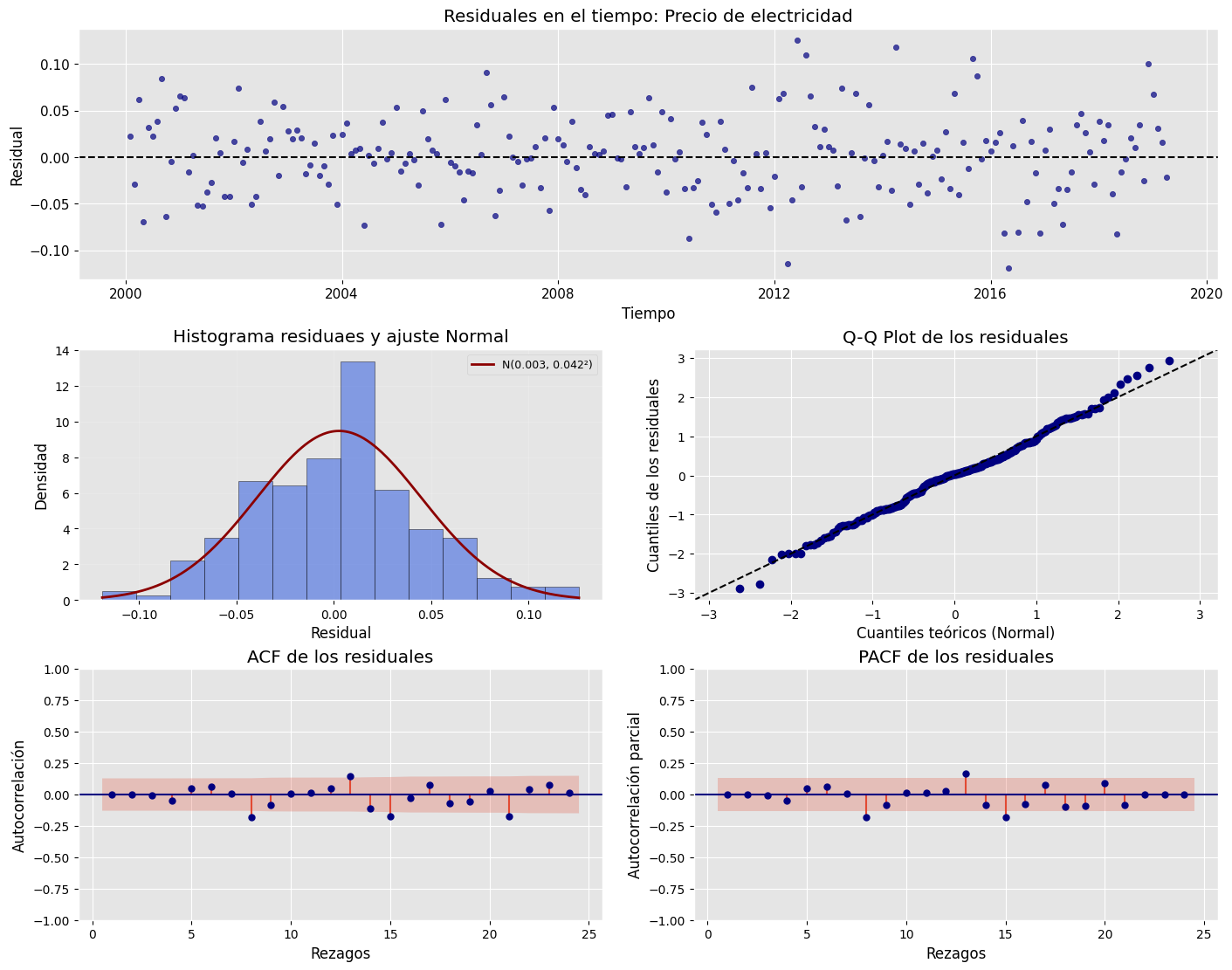
Análisis de los residuales#
analisis_residuales(
results.resid, # Agregar los residuales
nombre="Precio de electricidad",
)
Métricas de desempeño#
from sklearn.metrics import (
r2_score,
mean_squared_error,
mean_absolute_percentage_error,
max_error
)
metricas = evaluar_metricas_desempeno(
train=train,
test=test,
results=results,
transformacion='boxcox', # 'log', 'boxcox', 'sqrt' o None
lambda_bc=lambda_bc, # Solo si es boxcox
nombre="MA(0,1,3) Precio de electricidad"
)
Métricas de desempeño - MA(0,1,3) Precio de electricidad
--------------------------------------------------------
| Train | Test | |
|---|---|---|
| RMSE | 70.2417 | 124.5009 |
| MAPE (%) | 18.9839 | 25.7196 |
| Max Error | 713.0117 | 487.2253 |
| R2 | 0.7107 | 0.6452 |
| R2 Ajustado | 0.7095 | 0.6390 |
ARIMA(3,1,3)#
# Definir los parámetros del modelo ARIMA (p, d, q)
order = (3, 1, 3) # Puedes ajustar según el análisis de ACF y PACF
trend = 'n' # 'c' = constante, 't' = tendencia, 'ct' = constante + tendencia, 'n' = sin tendencia
seasonal_order = (0, 0, 0, 0) # Parámetros de la estacionalidad (P, D, Q, s)
# Ajustar el modelo con los datos de entrenamiento
model = SARIMAX(train, order=order, seasonal_order=seasonal_order, trend=trend)
results = model.fit()
# Mostrar resumen del modelo
print(results.summary())
SARIMAX Results
==============================================================================
Dep. Variable: Precio_boxcox No. Observations: 232
Model: SARIMAX(3, 1, 3) Log Likelihood 411.791
Date: Mon, 24 Nov 2025 AIC -809.582
Time: 19:08:20 BIC -785.485
Sample: 01-01-2000 HQIC -799.863
- 04-01-2019
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 1.8312 0.078 23.456 0.000 1.678 1.984
ar.L2 -1.7993 0.080 -22.546 0.000 -1.956 -1.643
ar.L3 0.8285 0.066 12.556 0.000 0.699 0.958
ma.L1 -1.9453 0.078 -25.071 0.000 -2.097 -1.793
ma.L2 1.8455 0.112 16.538 0.000 1.627 2.064
ma.L3 -0.8616 0.061 -14.227 0.000 -0.980 -0.743
sigma2 0.0016 0.000 10.728 0.000 0.001 0.002
===================================================================================
Ljung-Box (L1) (Q): 0.27 Jarque-Bera (JB): 2.15
Prob(Q): 0.60 Prob(JB): 0.34
Heteroskedasticity (H): 1.61 Skew: 0.19
Prob(H) (two-sided): 0.04 Kurtosis: 3.27
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
Ajuste y pronóstico en la serie original#
fitted_values = results.fittedvalues
y_pred_train = np.power((lambda_bc * fitted_values + 1), 1 / lambda_bc)
y_pred = y_pred_train[1:]
y_real = precio_electricidad["Precio"][1:split]
resultados = analizar_ajuste_serie(
precio_electricidad, # Serie original (sin transformar)
fitted_values, # Ajuste en train
results, # Modelo ajustado
test, # Datos test
n_forecast=12, # Periodos futuros
transformacion='boxcox', # 'log', 'boxcox', 'sqrt' o None
lambda_bc=lambda_bc, # Solo si es boxcox
nombre="Precio de electricidad"
)
### Gráfico de valores predichos vs. valores reales
plt.figure(figsize=(6,6))
plt.scatter(y_real, y_pred, color='blue', alpha=0.6, edgecolor='k')
# Línea de identidad (y = x)
min_val = min(y_real.min(), y_pred.min())
max_val = max(y_real.max(), y_pred.max())
plt.plot([min_val, max_val], [min_val, max_val], color='black', lw=2)
plt.title("Valores predichos vs. valores reales", fontsize=12)
plt.xlabel("Valores reales")
plt.ylabel("Valores predichos")
plt.axis("equal") # asegura proporciones iguales para la diagonal
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()
Análisis de los residuales#
analisis_residuales(
results.resid, # Agregar los residuales
nombre="Precio de electricidad",
)
Métricas de desempeño#
metricas = evaluar_metricas_desempeno(
train=train,
test=test,
results=results,
transformacion='boxcox', # 'log', 'boxcox', 'sqrt' o None
lambda_bc=lambda_bc, # Solo si es boxcox
nombre="ARIMA(3,1,3) Precio de electricidad"
)
Métricas de desempeño - ARIMA(3,1,3) Precio de electricidad
-----------------------------------------------------------
| Train | Test | |
|---|---|---|
| RMSE | 68.3017 | 130.4160 |
| MAPE (%) | 18.1770 | 24.8115 |
| Max Error | 688.9788 | 565.0481 |
| R2 | 0.7265 | 0.6107 |
| R2 Ajustado | 0.7253 | 0.6038 |
SARIMA(3,1,3)(1,0,1,12)#
# Definir los parámetros del modelo ARIMA (p, d, q)
order = (3, 1, 3) # Puedes ajustar según el análisis de ACF y PACF
trend = 'n' # 'c' = constante, 't' = tendencia, 'ct' = constante + tendencia, 'n' = sin tendencia
seasonal_order = (1, 0, 1, 12) # Parámetros de la estacionalidad (P, D, Q, s)
# Ajustar el modelo con los datos de entrenamiento
model = SARIMAX(train, order=order, seasonal_order=seasonal_order, trend=trend)
results = model.fit()
# Mostrar resumen del modelo
print(results.summary())
SARIMAX Results
============================================================================================
Dep. Variable: Precio_boxcox No. Observations: 232
Model: SARIMAX(3, 1, 3)x(1, 0, [1], 12) Log Likelihood 411.734
Date: Mon, 24 Nov 2025 AIC -805.469
Time: 19:08:30 BIC -774.487
Sample: 01-01-2000 HQIC -792.973
- 04-01-2019
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 1.8183 0.087 20.832 0.000 1.647 1.989
ar.L2 -1.7735 0.098 -18.106 0.000 -1.965 -1.581
ar.L3 0.8068 0.070 11.512 0.000 0.669 0.944
ma.L1 -1.9440 0.092 -21.073 0.000 -2.125 -1.763
ma.L2 1.8296 0.143 12.802 0.000 1.549 2.110
ma.L3 -0.8461 0.077 -10.997 0.000 -0.997 -0.695
ar.S.L12 0.2034 11.162 0.018 0.985 -21.674 22.080
ma.S.L12 -0.1974 11.149 -0.018 0.986 -22.048 21.653
sigma2 0.0016 0.000 9.858 0.000 0.001 0.002
===================================================================================
Ljung-Box (L1) (Q): 0.13 Jarque-Bera (JB): 1.69
Prob(Q): 0.72 Prob(JB): 0.43
Heteroskedasticity (H): 1.61 Skew: 0.17
Prob(H) (two-sided): 0.04 Kurtosis: 3.25
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
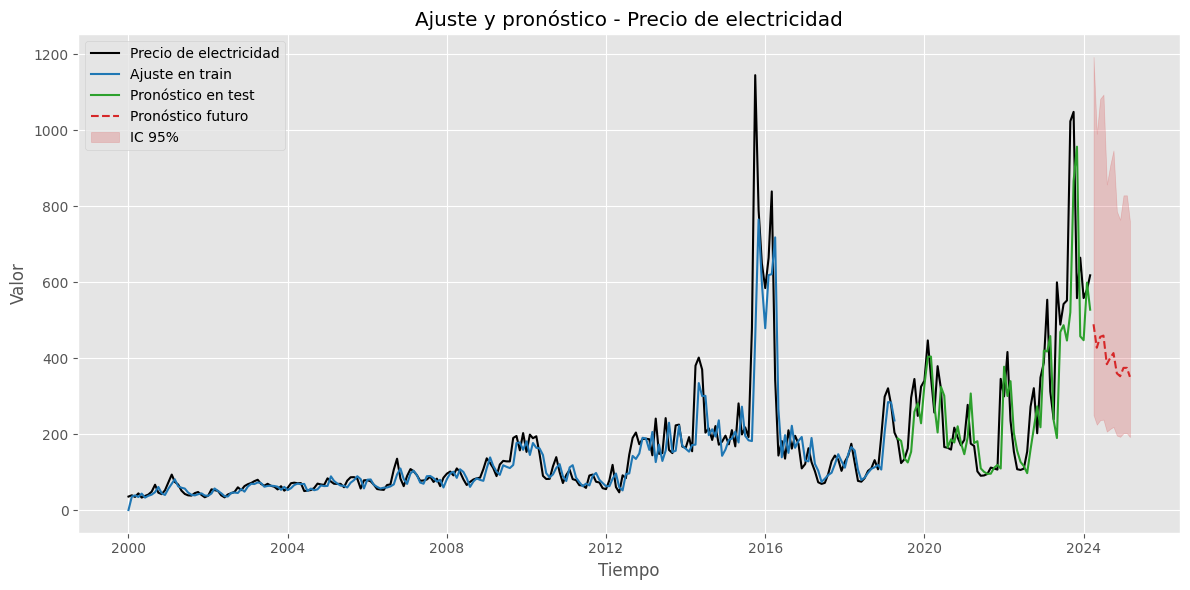
Ajuste y pronóstico en la serie original#
fitted_values = results.fittedvalues
y_pred_train = np.power((lambda_bc * fitted_values + 1), 1 / lambda_bc)
y_pred = y_pred_train[1:]
y_real = precio_electricidad["Precio"][1:split]
resultados = analizar_ajuste_serie(
precio_electricidad, # Serie original (sin transformar)
fitted_values, # Ajuste en train
results, # Modelo ajustado
test, # Datos test
n_forecast=12, # Periodos futuros
transformacion='boxcox', # 'log', 'boxcox', 'sqrt' o None
lambda_bc=lambda_bc, # Solo si es boxcox
nombre="Precio de electricidad"
)
### Gráfico de valores predichos vs. valores reales
plt.figure(figsize=(6,6))
plt.scatter(y_real, y_pred, color='blue', alpha=0.6, edgecolor='k')
# Línea de identidad (y = x)
min_val = min(y_real.min(), y_pred.min())
max_val = max(y_real.max(), y_pred.max())
plt.plot([min_val, max_val], [min_val, max_val], color='black', lw=2)
plt.title("Valores predichos vs. valores reales", fontsize=12)
plt.xlabel("Valores reales")
plt.ylabel("Valores predichos")
plt.axis("equal") # asegura proporciones iguales para la diagonal
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()
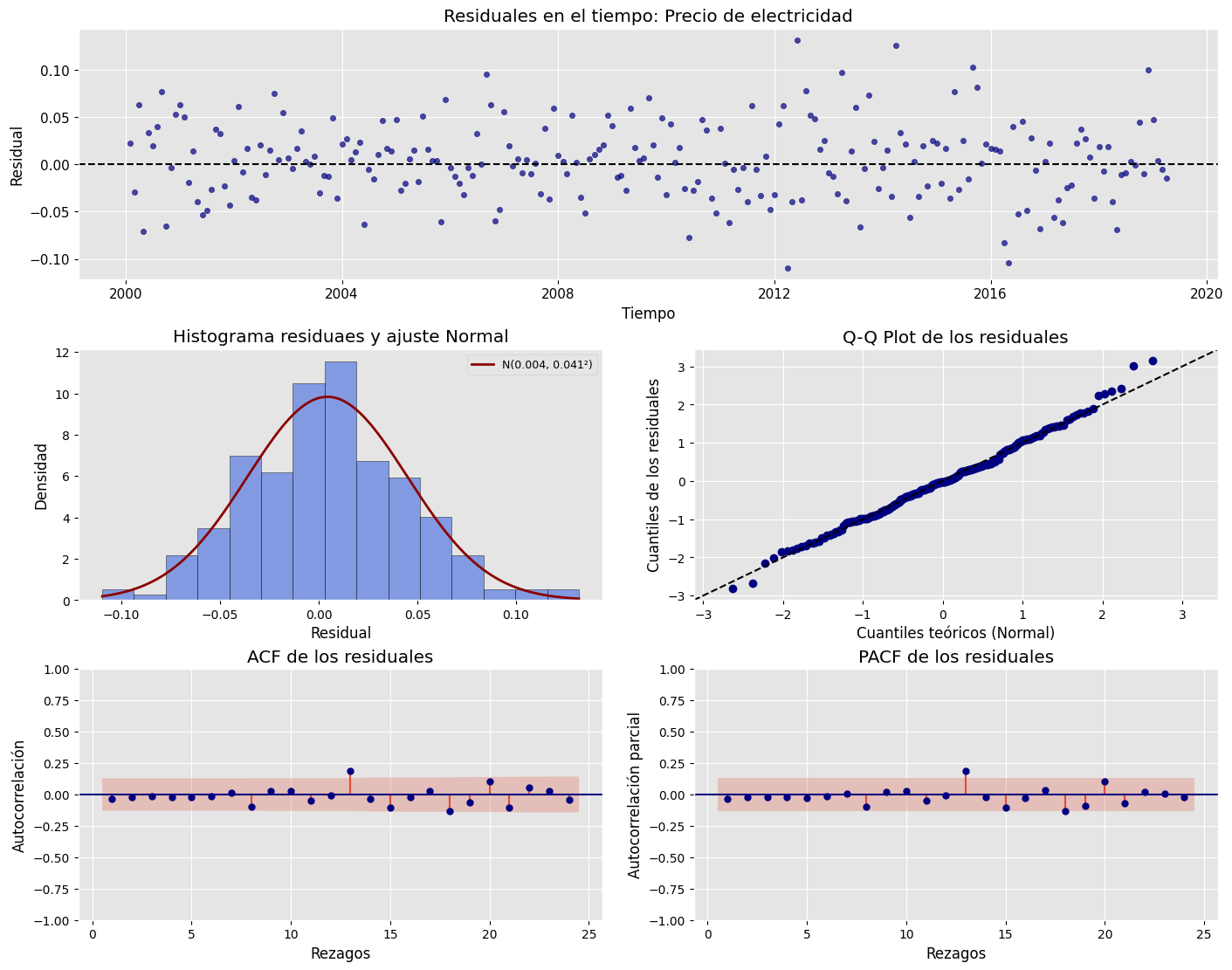
Análisis de los residuales#
analisis_residuales(
results.resid, # Agregar los residuales
nombre="Precio de electricidad",
)
Métricas de desempeño#
metricas = evaluar_metricas_desempeno(
train=train,
test=test,
results=results,
transformacion='boxcox', # 'log', 'boxcox', 'sqrt' o None
lambda_bc=lambda_bc, # Solo si es boxcox
nombre="SARIMA(3,1,3)(1,0,1,12) Precio de electricidad"
)
Métricas de desempeño - SARIMA(3,1,3)(1,0,1,12) Precio de electricidad
----------------------------------------------------------------------
| Train | Test | |
|---|---|---|
| RMSE | 68.4205 | 130.0571 |
| MAPE (%) | 18.2000 | 24.8158 |
| Max Error | 692.8142 | 566.1221 |
| R2 | 0.7256 | 0.6128 |
| R2 Ajustado | 0.7244 | 0.6060 |
**Dado que el rezago 13 sigue presentándose como ligeramente significativo, se evaluaron varios modelos SARIMA con rezagos mayores al del modelo previo. Como resultado, se determinó que el modelo SARIMA(8,1,8)(1,0,1)_{12} satisface este requisito en los residuales.**
SARIMA(8,1,8)(1,0,1,12)#
# Definir los parámetros del modelo ARIMA (p, d, q)
order = (8, 1, 8) # Puedes ajustar según el análisis de ACF y PACF
trend = 'n' # 'c' = constante, 't' = tendencia, 'ct' = constante + tendencia, 'n' = sin tendencia
seasonal_order = (1, 0, 1, 12) # Parámetros de la estacionalidad (P, D, Q, s)
# Ajustar el modelo con los datos de entrenamiento
model = SARIMAX(train, order=order, seasonal_order=seasonal_order, trend=trend)
results = model.fit()
# Mostrar resumen del modelo
print(results.summary())
SARIMAX Results
============================================================================================
Dep. Variable: Precio_boxcox No. Observations: 232
Model: SARIMAX(8, 1, 8)x(1, 0, [1], 12) Log Likelihood 414.788
Date: Mon, 24 Nov 2025 AIC -791.577
Time: 19:09:03 BIC -726.171
Sample: 01-01-2000 HQIC -765.196
- 04-01-2019
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 -0.1067 0.326 -0.327 0.743 -0.745 0.532
ar.L2 -0.1240 0.275 -0.451 0.652 -0.663 0.415
ar.L3 -0.1392 0.271 -0.514 0.607 -0.669 0.391
ar.L4 0.0362 0.302 0.120 0.905 -0.557 0.629
ar.L5 -0.1889 0.214 -0.882 0.378 -0.609 0.231
ar.L6 0.0981 0.238 0.413 0.680 -0.368 0.564
ar.L7 0.2871 0.242 1.188 0.235 -0.187 0.761
ar.L8 -0.0163 0.287 -0.057 0.955 -0.578 0.546
ma.L1 -0.0245 0.318 -0.077 0.939 -0.647 0.598
ma.L2 -0.0313 0.275 -0.114 0.909 -0.570 0.507
ma.L3 -0.0238 0.292 -0.081 0.935 -0.596 0.549
ma.L4 -0.1544 0.300 -0.514 0.607 -0.743 0.434
ma.L5 0.1954 0.230 0.850 0.396 -0.255 0.646
ma.L6 -0.0797 0.256 -0.311 0.756 -0.582 0.422
ma.L7 -0.3733 0.264 -1.416 0.157 -0.890 0.143
ma.L8 -0.2459 0.309 -0.796 0.426 -0.851 0.359
ar.S.L12 0.2274 1.094 0.208 0.835 -1.918 2.372
ma.S.L12 -0.1559 1.139 -0.137 0.891 -2.389 2.077
sigma2 0.0015 0.000 10.084 0.000 0.001 0.002
===================================================================================
Ljung-Box (L1) (Q): 0.03 Jarque-Bera (JB): 0.35
Prob(Q): 0.87 Prob(JB): 0.84
Heteroskedasticity (H): 1.48 Skew: 0.09
Prob(H) (two-sided): 0.09 Kurtosis: 2.97
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
Ajuste y pronóstico en la serie original#
fitted_values = results.fittedvalues
y_pred_train = np.power((lambda_bc * fitted_values + 1), 1 / lambda_bc)
y_pred = y_pred_train[1:]
y_real = precio_electricidad["Precio"][1:split]
resultados = analizar_ajuste_serie(
precio_electricidad, # Serie original (sin transformar)
fitted_values, # Ajuste en train
results, # Modelo ajustado
test, # Datos test
n_forecast=12, # Periodos futuros
transformacion='boxcox', # 'log', 'boxcox', 'sqrt' o None
lambda_bc=lambda_bc, # Solo si es boxcox
nombre="Precio de electricidad"
)
### Gráfico de valores predichos vs. valores reales
plt.figure(figsize=(6,6))
plt.scatter(y_real, y_pred, color='blue', alpha=0.6, edgecolor='k')
# Línea de identidad (y = x)
min_val = min(y_real.min(), y_pred.min())
max_val = max(y_real.max(), y_pred.max())
plt.plot([min_val, max_val], [min_val, max_val], color='black', lw=2)
plt.title("Valores predichos vs. valores reales", fontsize=12)
plt.xlabel("Valores reales")
plt.ylabel("Valores predichos")
plt.axis("equal") # asegura proporciones iguales para la diagonal
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()
Análisis de los residuales#
analisis_residuales(
results.resid, # Agregar los residuales
nombre="Precio de electricidad",
)
Métricas de desempeño:#
metricas = evaluar_metricas_desempeno(
train=train,
test=test,
results=results,
transformacion='boxcox', # 'log', 'boxcox', 'sqrt' o None
lambda_bc=lambda_bc, # Solo si es boxcox
nombre="SARIMA(8,1,8)(1,0,1,12) Precio de electricidad"
)
Métricas de desempeño - SARIMA(8,1,8)(1,0,1,12) Precio de electricidad
----------------------------------------------------------------------
| Train | Test | |
|---|---|---|
| RMSE | 66.2993 | 130.5171 |
| MAPE (%) | 18.0797 | 25.6725 |
| Max Error | 691.2980 | 502.5409 |
| R2 | 0.7423 | 0.6101 |
| R2 Ajustado | 0.7412 | 0.6032 |