Solución taller AR-TRM semanal#
Descargar la TRM semanal desde 2017-01-01 hasta 2025-07-31.
Responder las siguientes preguntas:
1. Seleccione la respuesta correcta:
La ACF de la transformación logarítmica indica que la serie transformada presenta tendencia, por lo tanto, no es estacionaria en tendencia.
El valor \(p\) de la prueba ADF aplicada a la serie transformada en logaritmo es mayor que \(0,05\), por lo que la serie transformada no es estacionaria.
La ACF del logaritmo de la serie muestra un decaimiento lento, lo que sugiere dependencia del pasado; asimismo, la PACF confirma que el primer rezago de la serie transformada tiene una autocorrelación parcial significativa y alta. Dado que la serie transformada es estacionaria, es adecuado ajustar un modelo AR(1).
Ninguna de las anteriores es correcta.
Respuesta correcta: A
El decaimiento lento observado en la ACF indica la presencia de una tendencia. Esto se confirma en el gráfico de la serie transformada y, además, la prueba ADF presenta un valor \(p = 0,5536\), el cual es mayor que \(0,05\), evidenciando que la serie no es estacionaria.
2. La serie de tiempo transformada en su primera diferencia y la serie transformada en la primera diferencia del logaritmo son casi iguales; únicamente cambia la escala, pero ambas muestran comportamientos muy similares. Asimismo, la ACF y la PACF de ambas series presentan patrones casi idénticos. Además, los estadísticos ADF de las dos transformaciones son muy cercanos.
Verdadero.
Falso.
Respuesta correcta: verdadero
3. Seleccione la respuesta correcta:
Como la serie original muestra una ACF con decaimiento lento, esto sugiere relación con rezagos pasados. Asimismo, la PACF evidencia una alta autocorrelación parcial en el primer rezago, lo que confirmaría la pertinencia de un modelo autorregresivo de orden 1. Sin embargo, dado que la serie original no es estacionaria, lo más apropiado sería aplicar el modelo AR(1) a la serie transformada en su primera diferencia.
Dado que los modelos AR solo se recomiendan para series estacionarias y que únicamente la serie transformada en su primera diferencia y la primera diferencia del logaritmo cumplen esta condición, y considerando que ambas presentan autocorrelaciones y autocorrelaciones parciales muy cercanas a las bandas de significancia, no sería adecuado ajustar un modelo AR, ya que estas transformaciones se asemejan a un ruido blanco.
La primera diferencia de la serie muestra una ACF con autocorrelaciones ligeramente significativas en los primeros cuatro rezagos; a partir del quinto rezago, la autocorrelación se aproxima a cero, lo que sugiere una relación con el pasado. Además, la PACF indica autocorrelaciones parciales levemente significativas hasta el cuarto rezago. Dado que esta serie transformada es estacionaria, podría ajustarse un modelo AR probando rezagos entre 1 y 4.
Ninguna de las anteriores es correcta.
Respuesta correcta: C
Se podría ajustar un modelo AR con hasta \(p = 4\) para evaluar la significancia de los rezagos.
La opción A no es correcta, dado que el análisis de los rezagos y la estacionariedad debe realizarse sobre la serie que se va a ajustar; no se debe extrapolar que, si la serie original podría seguir un modelo AR, entonces sus transformaciones también lo harán.
La opción B tampoco es correcta, ya que sí es posible ajustar un modelo AR y obtener rezagos significativos; por lo tanto, la serie transformada no corresponde a un ruido blanco.
Ajuste de modelos AR
Para realizar el ajuste del modelo autorregresivo, utilice como conjunto de test el último 20% de la serie de tiempo, ya sea la serie original o su versión transformada.
4. Luego de ajustar un modelo AR(1) a la serie transformada en su primera diferencia, seleccione la respuesta correcta:
El ajuste AR(1) es significativo, dado que tanto la constante \(\alpha\) como el coeficiente \(\phi_1\) no son cercanos a cero, sus valores \(z\) son mayores que el \(z_{crítico}\) (1,96 o 2,58), los valores \(p\) son menores que 0,05 y en los intervalos de confianza no se incluye el cero.
El ajuste AR(1) es significativo, dado que el coeficiente \(\phi_1\) no es cercano a cero, su valor \(z\) es mayor que el \(z_{crítico}\) (1,96 o 2,58), el valor \(p\) es menor que 0,05 y en el intervalo de confianza no se incluye el cero.
En el ajuste AR(1) a la serie transformada en su primera diferencia no se consideran ni la constante \(\alpha\) ni la tendencia \(\beta_t\); sin embargo, el coeficiente \(\phi_1\) no es significativo, ya que su valor \(p\) es mayor que 0,05.
Ninguna de las anteriores es correcta.
Respuesta correcta: B
Las opciones A y C no son correctas porque mencionan el intercepto \(\alpha\) y la tendencia \(\beta_t\), los cuales no se evalúan cuando se aplica la transformación por diferencias.
En este tipo de transformación, la serie resultante queda centrada, por lo que no se debe incluir :math:`beta_t`, y además inicia en un valor cercano a cero, motivo por el cual no se debe considerar :math:`alpha`.
5. Luego de ajustar un modelo AR(2) a la serie transformada en su primera diferencia, seleccione la respuesta correcta:
El coeficiente \(\phi_1\) del modelo AR(2) es significativo al 5%, ya que su valor \(z\) es mayor que el valor crítico de 1,96. Sin embargo, para un nivel de significancia del 1%, este coeficiente no resulta significativo, dado que \(|z| = 2{,}370\) es menor que el valor crítico de 2,58. Además, \(\phi_1 = -0{,}0989\) es un valor pequeño y más cercano a cero que \(\phi_2 = 0{,}1188\); no obstante, en términos generales, el ajuste puede considerarse significativo.
Como \(\phi_1 = -0{,}0989\), este valor negativo indicaría que el modelo AR(2) no es significativo, ya que el coeficiente del primer rezago es negativo.
En el pronóstico fuera de la muestra, realizado 12 semanas después del conjunto de test, el resultado es completamente bajista.
Ninguna de las anteriores es correcta.
Respuesta correcta: A
La opción B no es correcta, ya que el signo del coeficiente no determina la significancia estadística; este únicamente indica si la relación entre el rezago y la serie ajustada es directa o inversa.
La opción C tampoco es correcta, porque el pronóstico descrito no presenta un comportamiento bajista según los resultados obtenidos.
6. Luego de ajustar un modelo AR(3) a la serie transformada en su primera diferencia, seleccione la respuesta correcta:
Se podría considerar que el ajuste AR(3) es significativo, dado que presenta coeficientes estadísticamente significativos, y únicamente el coeficiente del primer rezago es ligeramente no significativo.
En el pronóstico fuera de la muestra, realizado 12 semanas después del conjunto de test, el resultado muestra un comportamiento totalmente bajista.
El ajuste AR(3) no es significativo, ya que el coeficiente \(\phi_1\) no resulta significativo ni al 5% (\(z_{crítico}=1{,}96\)), su valor \(p\) es mayor que 0,05 y el intervalo de confianza incluye el valor cero, a pesar de que los demás coeficientes sí son significativos.
Ninguna de las anteriores es correcta.
Respuesta correcta: C
7. Luego de ajustar un modelo AR(4) a la serie transformada en su primera diferencia, responda lo siguiente:
El ajuste del modelo AR(4) es significativo, ya que los coeficientes estimados de los rezagos no se aproximan a cero, los valores absolutos de \(z\) son significativos al 5% (\(z_{crítico}=1{,}96\)), todos los valores \(p\) son menores que 0,05 y ninguno de los intervalos de confianza incluye el valor cero.
Verdadero.
Falso.
Respuesta correcta: verdadero
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
def analisis_estacionariedad(
serie: pd.Series,
nombre: str = None,
lags: int = 24,
xtick_interval: int = 3
):
"""
Gráfica y análisis de estacionariedad para una serie de tiempo:
- Serie original, diferencia, logaritmo y diferencia del logaritmo.
- Muestra la ACF, PACF y resultado ADF en subplots.
Args:
serie: Serie de tiempo (índice datetime, pandas.Series)
nombre: Nombre de la serie (para títulos)
lags: Número de rezagos para ACF/PACF
xtick_interval: Mostrar ticks en X cada este número de lags, incluyendo siempre el lag 1
"""
if nombre is None:
nombre = serie.name if serie.name is not None else "Serie"
# Transformaciones
serie_1 = serie.copy()
serie_2 = serie_1.diff().dropna()
serie_3 = np.log(serie_1)
serie_4 = serie_3.diff().dropna()
titulos = [
f"Serie original: {nombre}",
"Diferenciación",
"Logaritmo",
"Diferenciación del Logaritmo"
]
series = [serie_1, serie_2, serie_3, serie_4]
resultados_adf = []
interpretaciones = []
for i, serie_i in enumerate(series):
serie_ = serie_i.dropna()
# Selección de regresión en ADF
if i in [0, 2]:
adf = adfuller(serie_, regression='ct')
else:
adf = adfuller(serie_, regression='c')
estadistico = adf[0]
pvalue = adf[1]
resultados_adf.append((estadistico, pvalue))
interpretaciones.append("Estacionaria" if pvalue < 0.05 else "No estacionaria")
fig, axes = plt.subplots(4, 3, figsize=(18, 16))
colores = ['black', 'black', 'black', 'black']
for fila in range(4):
# Serie y etiquetas
axes[fila, 0].plot(series[fila], color=colores[fila])
axes[fila, 0].set_title(titulos[fila], color='black')
axes[fila, 0].set_xlabel("Fecha", color='black')
if fila == 0:
axes[fila, 0].set_ylabel("Valor", color='black')
elif fila == 1:
axes[fila, 0].set_ylabel("Δ Valor", color='black')
elif fila == 2:
axes[fila, 0].set_ylabel("Log(Valor)", color='black')
else:
axes[fila, 0].set_ylabel("Δ Log(Valor)", color='black')
axes[fila, 0].grid(True, alpha=0.3)
axes[fila, 0].tick_params(axis='both', labelsize=11, colors='black')
# ACF
plot_acf(
series[fila].dropna(),
lags=lags,
ax=axes[fila, 1],
zero=False,
color=colores[fila]
)
axes[fila, 1].set_title("ACF", color='black')
# xticks: incluir lag 1 y luego cada xtick_interval (ej: 1, 3, 6, ...)
xticks = [1] + list(range(xtick_interval, lags + 1, xtick_interval))
xticks = sorted(set(xticks)) # asegura que no haya duplicados
axes[fila, 1].set_xticks(xticks)
axes[fila, 1].tick_params(axis='both', labelsize=11, colors='black')
axes[fila, 1].set_xlabel("Lag", color='black')
axes[fila, 1].set_ylabel("Autocorrelación", color='black')
# PACF
plot_pacf(
series[fila].dropna(),
lags=lags,
ax=axes[fila, 2],
zero=False,
color=colores[fila]
)
axes[fila, 2].set_title("PACF", color='black')
axes[fila, 2].set_xticks(xticks)
axes[fila, 2].tick_params(axis='both', labelsize=11, colors='black')
axes[fila, 2].set_xlabel("Lag", color='black')
axes[fila, 2].set_ylabel("Autocorrelación parcial", color='black')
# Indicador estacionariedad (más abajo)
axes[fila, 0].text(
0.02, 0.85,
f"ADF: {resultados_adf[fila][0]:.2f}\np-valor: {resultados_adf[fila][1]:.4f}\n{interpretaciones[fila]}",
transform=axes[fila, 0].transAxes,
fontsize=11, bbox=dict(facecolor='white', alpha=0.85), color='black'
)
plt.tight_layout()
plt.show()
# Devuelve los resultados en un dict (opcional)
adf_dict = {
titulos[i]: {
"estadístico ADF": resultados_adf[i][0],
"p-valor": resultados_adf[i][1],
"interpretación": interpretaciones[i]
}
for i in range(4)
}
return adf_dict
import yfinance as yf
# Descargar datos mensuales desde 2015
start_date = "2017-01-01"
end_date = "2025-07-31"
# TRM de Colombia (USD/COP)
trm = yf.download("USDCOP=X", start=start_date, end=end_date, interval='1wk', auto_adjust=False)['Close']
trm.name = 'TRM (USD/COP)'
# Crear figura
plt.figure(figsize=(10, 5))
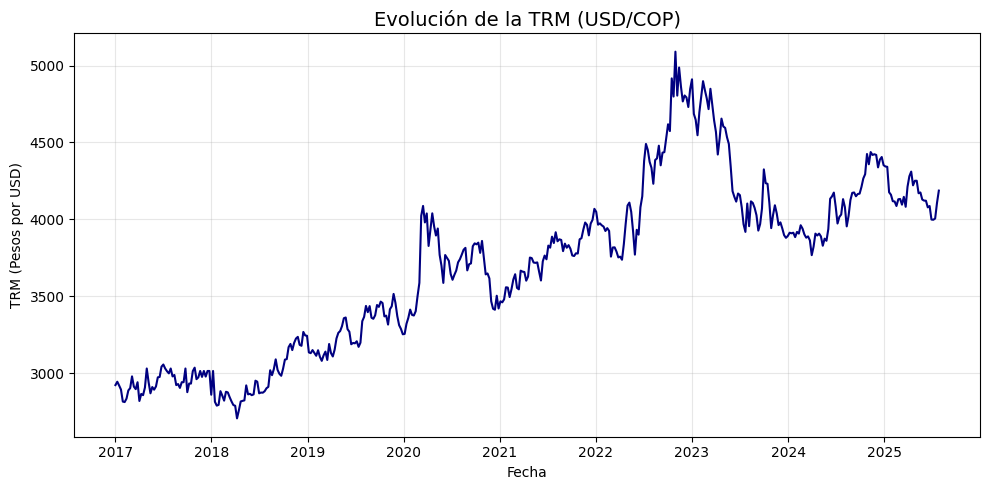
plt.plot(trm.index, trm, linestyle='-', color='navy')
# Personalización del gráfico
plt.title("Evolución de la TRM (USD/COP)", fontsize=14)
plt.xlabel("Fecha")
plt.ylabel("TRM (Pesos por USD)")
plt.grid(True, alpha=0.3)
# Formato de fechas en el eje X
plt.gca().xaxis.set_major_locator(mdates.YearLocator())
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter('%Y'))
plt.tight_layout()
plt.show()
[*******************100%*********************] 1 of 1 completed
adf_resultados = analisis_estacionariedad(
trm['USDCOP=X'],
nombre="TRM semanal",
lags=24,
xtick_interval=3
)
# Establecer frecuencia explícita para evitar el warning de statsmodels
trm.index.freq = trm.index.inferred_freq
Conjunto de train y test:#
# Dividir en train y test (por ejemplo, 80% train, 20% test)
split = int(len(trm) * 0.8)
train, test = trm[:split], trm[split:]
# Graficar train y test:
plt.figure(figsize=(12, 5))
plt.plot(train, label='Train', color='navy')
plt.plot(test, label='Test', color='orange')
plt.title("Conjunto de train y test")
plt.xlabel("Fecha")
plt.ylabel("Valor")
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
Ajuste AR(1)#
from statsmodels.tsa.statespace.sarimax import SARIMAX
Para la primera diferencia se debe indicar trend='n'. Además, se
debe utilizar el conjunto de entrenamiento de la serie original, ya que
al establecer d=1, la función SARIMAX aplica automáticamente la
transformación en primera diferencia.
# Definir los parámetros del modelo AR (p, d, 0)
order = (1, 1, 0) # Puedes ajustar según el análisis de ACF y PACF
trend = 'n' # 'c' = constante, 't' = tendencia, 'ct' = constante + tendencia, 'n' = sin tendencia
# Ajustar el modelo con los datos de entrenamiento
model = SARIMAX(train, order=order, trend=trend)
results = model.fit()
# Mostrar resumen del modelo
print(results.summary())
SARIMAX Results
==============================================================================
Dep. Variable: USDCOP=X No. Observations: 358
Model: SARIMAX(1, 1, 0) Log Likelihood -2078.750
Date: Wed, 22 Oct 2025 AIC 4161.499
Time: 16:18:56 BIC 4169.255
Sample: 01-01-2017 HQIC 4164.584
- 11-05-2023
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 -0.1115 0.040 -2.779 0.005 -0.190 -0.033
sigma2 6702.9791 310.826 21.565 0.000 6093.771 7312.187
===================================================================================
Ljung-Box (L1) (Q): 0.04 Jarque-Bera (JB): 169.41
Prob(Q): 0.83 Prob(JB): 0.00
Heteroskedasticity (H): 3.52 Skew: 0.61
Prob(H) (two-sided): 0.00 Kurtosis: 6.15
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
Ajuste AR(2)#
# Definir los parámetros del modelo AR (p, d, 0)
order = (2, 1, 0) # Puedes ajustar según el análisis de ACF y PACF
trend = 'n' # 'c' = constante, 't' = tendencia, 'ct' = constante + tendencia, 'n' = sin tendencia
# Ajustar el modelo con los datos de entrenamiento
model = SARIMAX(train, order=order, trend=trend)
results = model.fit()
# Mostrar resumen del modelo
print(results.summary())
SARIMAX Results
==============================================================================
Dep. Variable: USDCOP=X No. Observations: 358
Model: SARIMAX(2, 1, 0) Log Likelihood -2076.234
Date: Wed, 22 Oct 2025 AIC 4158.469
Time: 16:18:56 BIC 4170.102
Sample: 01-01-2017 HQIC 4163.096
- 11-05-2023
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 -0.0989 0.042 -2.370 0.018 -0.181 -0.017
ar.L2 0.1188 0.041 2.902 0.004 0.039 0.199
sigma2 6625.5240 344.108 19.254 0.000 5951.084 7299.964
===================================================================================
Ljung-Box (L1) (Q): 0.07 Jarque-Bera (JB): 124.65
Prob(Q): 0.79 Prob(JB): 0.00
Heteroskedasticity (H): 3.29 Skew: 0.53
Prob(H) (two-sided): 0.00 Kurtosis: 5.69
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
Ajuste AR(3)#
# Definir los parámetros del modelo AR (p, d, 0)
order = (3, 1, 0) # Puedes ajustar según el análisis de ACF y PACF
trend = 'n' # 'c' = constante, 't' = tendencia, 'ct' = constante + tendencia, 'n' = sin tendencia
# Ajustar el modelo con los datos de entrenamiento
model = SARIMAX(train, order=order, trend=trend)
results = model.fit()
# Mostrar resumen del modelo
print(results.summary())
SARIMAX Results
==============================================================================
Dep. Variable: USDCOP=X No. Observations: 358
Model: SARIMAX(3, 1, 0) Log Likelihood -2073.134
Date: Wed, 22 Oct 2025 AIC 4154.267
Time: 16:18:57 BIC 4169.778
Sample: 01-01-2017 HQIC 4160.437
- 11-05-2023
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 -0.0826 0.044 -1.868 0.062 -0.169 0.004
ar.L2 0.1052 0.042 2.532 0.011 0.024 0.187
ar.L3 -0.1322 0.046 -2.850 0.004 -0.223 -0.041
sigma2 6476.9994 331.291 19.551 0.000 5827.681 7126.318
===================================================================================
Ljung-Box (L1) (Q): 0.17 Jarque-Bera (JB): 143.62
Prob(Q): 0.68 Prob(JB): 0.00
Heteroskedasticity (H): 3.05 Skew: 0.53
Prob(H) (two-sided): 0.00 Kurtosis: 5.92
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
Ajuste AR(4)#
# Definir los parámetros del modelo AR (p, d, 0)
order = (4, 1, 0) # Puedes ajustar según el análisis de ACF y PACF
trend = 'n' # 'c' = constante, 't' = tendencia, 'ct' = constante + tendencia, 'n' = sin tendencia
# Ajustar el modelo con los datos de entrenamiento
model = SARIMAX(train, order=order, trend=trend)
results = model.fit()
# Mostrar resumen del modelo
print(results.summary())
SARIMAX Results
==============================================================================
Dep. Variable: USDCOP=X No. Observations: 358
Model: SARIMAX(4, 1, 0) Log Likelihood -2069.186
Date: Wed, 22 Oct 2025 AIC 4148.373
Time: 16:18:58 BIC 4167.761
Sample: 01-01-2017 HQIC 4156.084
- 11-05-2023
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 -0.1021 0.043 -2.347 0.019 -0.187 -0.017
ar.L2 0.1216 0.042 2.881 0.004 0.039 0.204
ar.L3 -0.1452 0.046 -3.171 0.002 -0.235 -0.055
ar.L4 -0.1490 0.049 -3.048 0.002 -0.245 -0.053
sigma2 6334.9143 321.990 19.674 0.000 5703.826 6966.002
===================================================================================
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 158.47
Prob(Q): 0.95 Prob(JB): 0.00
Heteroskedasticity (H): 2.99 Skew: 0.59
Prob(H) (two-sided): 0.00 Kurtosis: 6.04
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
###### Pronóstico dentro de la muestra (train) ######
fitted_values = results.fittedvalues
conf_int_train = results.get_prediction().conf_int(alpha=0.05) # Intervalo de confianza del 95%
# Alinear por si el índice de train y fitted_values difieren en los primeros p rezagos
fitted_values = fitted_values.reindex(train.index)
###### Pronóstico fuera de la muestra (test) #####
current_results = results # Modelo ajustado
forecasted_test = []
lower_ci_test = []
upper_ci_test = []
for i in range(len(test)):
forecaster = current_results.get_forecast(steps=1) # Un pronóstico hacia adelante
forecast_mean_test = forecaster.predicted_mean.iloc[0] # Media del pronóstico
ci_i_test = forecaster.conf_int(alpha=0.05).iloc[0] # Intervalo de confianza del 95%
forecasted_test.append(forecast_mean_test)
lower_ci_test.append(ci_i_test.iloc[0]) # límite inferior
upper_ci_test.append(ci_i_test.iloc[1]) # límite superior
# Actualiza el estado con el valor real (método recursivo)
current_results = current_results.append(endog=[test.iloc[i]], refit=False)
forecasted_test = pd.Series(forecasted_test, index=test.index, name='forecast_test')
lower_ci_test = pd.Series(lower_ci_test, index=test.index, name='lower_test')
upper_ci_test = pd.Series(upper_ci_test, index=test.index, name='upper_test')
###### Pronóstico fuera de la muestra: futuro #####
n_forecast = 12 # Pronóstico para 12 meses
# Actualiza el estado con el dataset de test
current_results = results.append(endog=test, refit=False)
forecasting = []
lower_ci = []
upper_ci = []
for i in range(n_forecast):
forecaster = current_results.get_forecast(steps=1) # Un pronóstico hacia adelante
forecast_mean = forecaster.predicted_mean.iloc[0] # Media del pronóstico
ci_i = forecaster.conf_int(alpha=0.05).iloc[0] # Intervalo de confianza del 95%
forecasting.append(forecast_mean)
lower_ci.append(ci_i.iloc[0]) # límite inferior
upper_ci.append(ci_i.iloc[1]) # límite superior
# Alimenta el modelo con el valor pronosticado (pronóstico puro hacia adelante)
current_results = current_results.append(endog=[forecast_mean], refit=False)
# Fechas futuras (mensuales inicio de mes)
last_date = test.index[-1]
future_dates = pd.date_range(start=last_date + pd.offsets.MonthBegin(1),
periods=n_forecast, freq='MS')
# Asegura Series con índice de fechas
forecasting = pd.Series(forecasting, index=future_dates, name='forecast')
lower_ci = pd.Series(lower_ci, index=future_dates, name='lower')
upper_ci = pd.Series(upper_ci, index=future_dates, name='upper')
##### Gráfico #####
plt.figure(figsize=(12, 6))
# Train y fitted
plt.plot(train[1:], label='Train', color='black')
plt.plot(fitted_values[1:], label='Ajuste en Train', color='tab:blue')
# Banda de confianza en train
plt.fill_between(conf_int_train[1:].index,
conf_int_train.iloc[1:, 0],
conf_int_train.iloc[1:, 1],
color='tab:blue', alpha=0.2, label='IC 95% - train')
# Test y forecast
plt.plot(test, label='Test', color='black', alpha=0.6)
plt.plot(test.index, forecasted_test, label='Pronóstico (test)', color='tab:green')
# Banda de confianza en test
plt.fill_between(lower_ci_test.index,
lower_ci_test,
upper_ci_test,
color='tab:green', alpha=0.2, label='IC 95% - test')
plt.plot(forecasting, label='Pronóstico (12 meses)', color='tab:red')
# Banda de confianza
plt.fill_between(future_dates,
lower_ci.values,
upper_ci.values,
color='tab:red', alpha=0.2, label='IC 95% - pronóstico')
plt.title('Ajuste y pronóstico')
plt.xlabel('Tiempo')
plt.ylabel('Valor')
plt.legend()
plt.tight_layout()
plt.show()