Regresión Logística#
La regresión logística es un clasificador binario que nos permite predecir la probabilidad de que algo ocurra o no ocurra.
La variable que queremos predecir (dependiente) solo puede tomar dos valores:
0 = “No” / “Fracaso” / “Falso”.
1 = “Sí” / “Éxito” / “Verdadero”.
Por ejemplo:
¿Un estudiante aprueba o no aprueba un examen?
¿Un cliente compra o no compra un producto?
¿Un correo es spam o no lo es?
En lugar de predecir directamente 0 o 1, el modelo estima la probabilidad de que ocurra el evento.
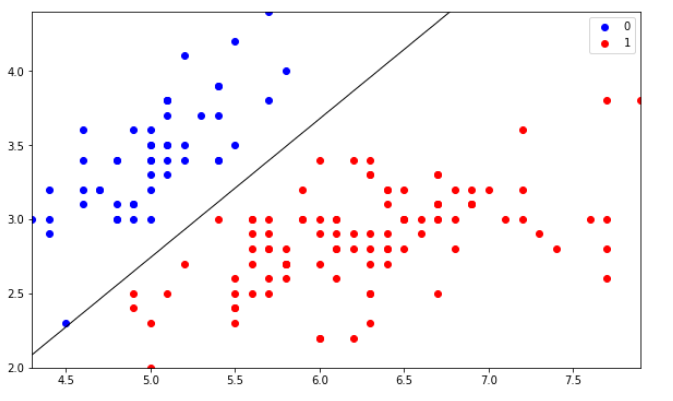
Data#
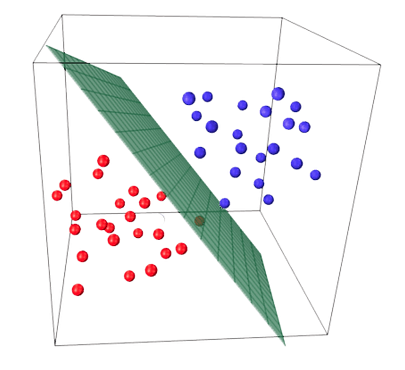
Data_3D#
Variable respuesta#
La variable respuesta \(y\) sigue una distribución de Bernoulli:
\(y = 1\) con probabilidad \(p\).
\(y = 0\) con probabilidad \(1-p\).
El valor esperado de \(y\) es \(p\), es decir, la probabilidad de que ocurra el evento.
La función logística o sigmoide#
Para transformar los valores a probabilidades, se usa una función en forma de “S”, llamada función logística:
donde \(z\) es una combinación lineal de las variables de entrada.
Esta función siempre entrega un valor entre 0 y 1, lo que la hace perfecta para interpretar resultados como probabilidades.
Ejemplo cotidiano:
Imagina que quieres predecir si lloverá mañana. No puedes decir “sí o no” con absoluta certeza, pero sí puedes dar una probabilidad: “hay un 70% de probabilidad de lluvia”. Ese es el papel de la función sigmoide.
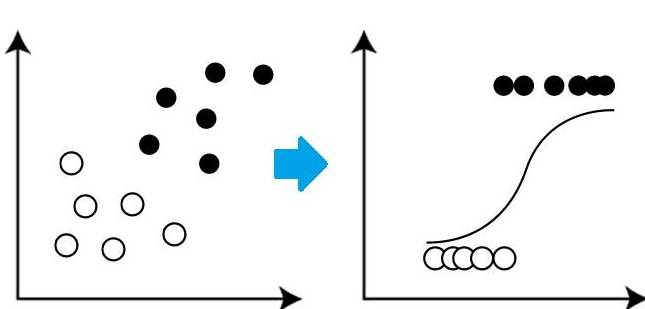
Data_trans#
S#
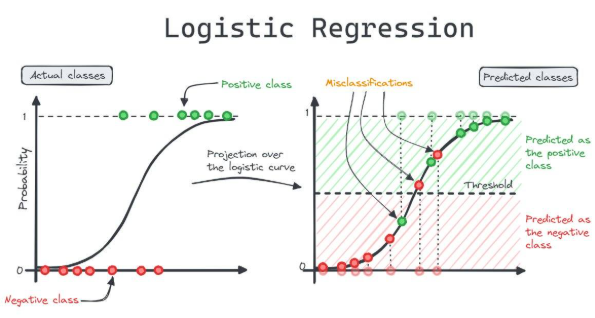
RL#
Umbral de decisión (Threshold)#
Una vez que tenemos la probabilidad, debemos decidir a qué clase pertenece cada observación.
Por defecto, se usa un umbral de 0,5:
Si \(p \geq 0,5\), clasificamos como 1 (éxito).
Si \(p < 0,5\), clasificamos como 0 (fracaso).
Ejemplo:
Si la probabilidad de que un cliente compre es 0,7 → se predice “Compra”.
Si la probabilidad es 0,3 → se predice “No compra”.
Este umbral puede ajustarse según el problema. Por ejemplo, en medicina, un umbral más bajo puede ser mejor para detectar enfermedades graves y reducir falsos negativos.
Regression#
Interpretación de los coeficientes#
En regresión logística no interpretamos los coeficientes directamente, sino los odds ratio.
La relación es:
Aplicando exponencial:
Ejemplo de interpretación:
Supongamos que \(\beta_1 = 0,1\).
Esto significa que un aumento unitario en \(X_1\) multiplica las probabilidades de éxito por \(e^{0,1} \approx 1,105\), es decir, un incremento del 10,5%.
Si \(\beta_1 = -0,1\), entonces \(e^{-0,1} \approx 0,905\), lo que reduce la probabilidad en un 9,5%.
Ejemplo cotidiano:
Si en cambio el coeficiente fuera negativo, cada hora extra podría reducir la probabilidad de aprobar (por ejemplo, si muchas horas generan fatiga).
Desventajas de la regresión logística#
1. Relación lineal entre variables independientes y el logit
2. Limitada a problemas binarios
3. Sensibilidad a outliers
4. Suposición de independencia entre variables
La regresión logística no maneja bien la multicolinealidad. En estos casos, conviene usar reducción de dimensionalidad (PCA) o algoritmos más robustos.
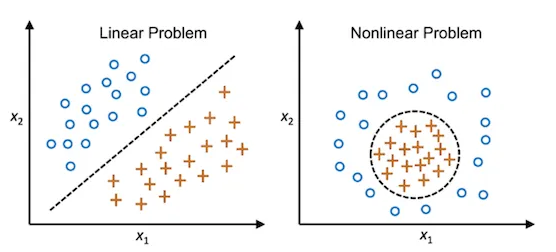
5. No captura relaciones complejas
En problemas donde la frontera entre clases es curva o muy irregular, algoritmos como SVM con kernels, árboles de decisión, random forest o redes neuronales suelen dar mejores resultados.
6. Problemas con datos desbalanceados
7. Escalabilidad limitada
En conjuntos de datos muy grandes, el entrenamiento puede volverse lento y costoso computacionalmente, sobre todo si hay muchas variables y se requiere ajuste fino.
8. Interpretación en modelos complejos
Aunque los coeficientes son interpretables en teoría, cuando el modelo tiene muchas variables o interacciones, la interpretación práctica se vuelve difícil y poco intuitiva.
Nonlinear#
No_S#
Ajuste en scikit-learn#
LogisticRegression()
Parámetro (valor por defecto) |
¿Para qué sirve? |
Cómo ajustarlo si hay sobreajuste (ove rfitting) |
Cómo ajustarlo si hay subajuste (unde rfitting) |
** Notas/compa tibilidad** |
|---|---|---|---|---|
C = 1.0 |
Controla la fuerza de regul arización (es 1/λ). |
Disminuye ``C`` (ej. 1 → 0.1 → 0.01) para más regu larización. |
Aumenta ``C`` (1 → 10 → 100) para menos regu larización. |
Es el parámetro más importante de tuning. Escalar datos ayuda a co nvergencia. |
penalty = ‘l2’ |
Tipo de regu larización. |
Mantén
|
Considera
|
|
solver = ‘lbfgs’ |
Algoritmo de op timización. |
Para
|
Para
multiclase
estable usa
|
|
c lass_weight = None |
Pondera clases (manejo de d esbalance). |
Usa
|
Aumenta peso de la minoritaria si la ignora. |
Complementa con ajuste del umbral tras entrenar. |
max_iter = 100 |
Número máximo de i teraciones. |
Sube a 300–1000 si no converge. |
— |
Escalar datos ayuda. Error “did not converge” ⇒ subir `` max_iter``. |
tol = 1e-4 |
Tolerancia de parada. |
Bájalo (1e-5, 1e-6) para ajuste más fino (más lento). |
Súbelo (1e-3) si ya es suficiente y quieres rapidez. |
Impacta tiempo de en trenamiento y co nvergencia. |
l1_ratio = None |
Mezcla
L1/L2 (solo
con
|
Súbelo hacia 1 para más sparsidad. |
Bájalo hacia 0 (más L2) si el modelo es muy simple. |
Requiere
``
penalty=’el
asticnet’``
y
|
fi t_intercept = True |
Añade intercepto (bias). |
Mantén True; ce ntra/escala features. |
Puede False si datos ya están centrados. |
Usualmente se deja en True. |
r andom_state = None |
Reprod ucibilidad. |
— |
— |
Fija un
número (ej.
35) para
resultados
repetibles,
sobre todo
con
|
n_jobs = None |
Núcleos de CPU (`` liblinear`` OVR). |
Usa -1 para p aralelizar. |
— |
Solo afecta a `` liblinear`` multiclase. |