Valoración de Opciones Financieras por Simulación Monte Carlo#
Acciones sin dividendos:#
La valoración de una opción financiera mediante el método de Simulación Monte Carlo implica simular múltiples trayectorias del precio del activo subyacente hasta la fecha de vencimiento de la opción, utilizando un modelo estocástico como el Movimiento Browniano Geométrico (GBM). Luego, se calcula el valor de la opción en cada trayectoria simulada al vencimiento y se toma el promedio de estos valores. Finalmente, este promedio se descuenta al presente utilizando la tasa de interés libre de riesgo. Este proceso se puede aplicar tanto a opciones de compra (call) como a opciones de venta (put).
A continuación, se detallan los pasos para valorar una opción de compra europea, aunque el proceso es similar para las opciones de venta:
Definir los parámetros iniciales: Estos incluyen el precio actual del activo subyacente (\(S\)), la tasa de interés libre de riesgo (\(r\)), la volatilidad del activo subyacente (\(\sigma\)), el tiempo hasta el vencimiento de la opción (\(T\)) y el precio de ejercicio de la opción (\(K\)).
Simular trayectorias del precio del activo subyacente: Utilizando el modelo de GBM, se generan múltiples trayectorias del precio del activo subyacente hasta la fecha de vencimiento de la opción. Cada trayectoria simula una posible evolución del precio del activo a lo largo del tiempo.
Calcular el valor de la opción en el vencimiento para cada trayectoria: Para una opción de compra, el valor al vencimiento es el máximo entre 0 y la diferencia entre el precio del activo subyacente y el precio de ejercicio \(Máx(S_T-K,0)\). Para una opción de venta, sería \(Máx(K-S_T,0)\).
Calcular el valor presente del promedio de los valores al vencimiento: Se toma el promedio de los valores calculados en el paso anterior y se descuenta al presente utilizando la tasa de interés libre de riesgo. La fórmula para el valor presente es: \(V_0=Promedio Valores Vencimiento \times e^{-rT}\).
Ajustar por el número de simulaciones: A medida que aumenta el número de trayectorias simuladas, la estimación del precio de la opción se vuelve más precisa.
import numpy as np
def valorar_opcion_europea_call(S0, K, T, r, sigma, num_simulaciones):
if seed is not None:
np.random.seed(seed) # Establecer la semilla
# Paso 2: Simular trayectorias del precio del activo subyacente
dt = T # Asumimos un paso de tiempo hasta el vencimiento
Z = np.random.standard_normal(num_simulaciones)
ST = S0 * np.exp((r - 0.5 * sigma**2) * dt + sigma * np.sqrt(dt) * Z)
# Paso 3: Calcular el valor de la opción en el vencimiento para cada trayectoria
payoff = np.maximum(ST - K, 0) # Para Put sería np.maximum(K - ST , 0)
# Paso 4: Calcular el valor presente del promedio de los valores al vencimiento
V0 = np.exp(-r * T) * np.mean(payoff)
return V0
# Parámetros de la opción
S0 = 100 # Precio inicial del activo subyacente
K = 105 # Precio de ejercicio de la opción
T = 1.0 # Tiempo hasta el vencimiento (en años)
r = 0.05 # Tasa de interés libre de riesgo expresada cómo Compuesta Continua Anual (CCA)
sigma = 0.2 # Volatilidad del activo subyacente
num_simulaciones = 10000 # Número de simulaciones
seed = 52 # Semilla para la reproducibilidad
# Valoración de la opción
precio_opcion = valorar_opcion_europea_call(S0, K, T, r, sigma, num_simulaciones)
print("El precio de la opción de compra europea es:", precio_opcion)
El precio de la opción de compra europea es: 7.958464828524326
Divisas:#
Para valorar opciones sobre divisas (también conocidas como opciones FX o de tipo de cambio) mediante el método de Simulación Monte Carlo, el proceso es muy similar al descrito para opciones sobre acciones. Sin embargo, hay algunas particularidades a considerar, como la tasa de interés en cada divisa.
Cuando se valora una opción sobre divisas, se debe tener en cuenta tanto la tasa de interés de la divisa nacional (doméstica) como la de la divisa extranjera. Esto se debe a que el tipo de cambio futuro está influenciado por la diferencia entre estas tasas de interés, según la paridad de interés cubierto. Por tanto, el modelo de GBM para el tipo de cambio se ajusta para incluir estas tasas.
Pasos para la Valoración de una Opción sobre Divisas:
Definir los parámetros iniciales: Estos incluyen el tipo de cambio actual (\(S_0\)), la tasa de interés libre de riesgo de la divisa nacional (\(r_d\)), la tasa de interés libre de riesgo de la divisa extranjera (\(r_f\)), la volatilidad del tipo de cambio (\(\sigma\)), el tiempo hasta el vencimiento de la opción (\(T\)) y el precio de ejercicio de la opción (\(K\)).
Simular trayectorias del tipo de cambio: Utilizando el modelo de GBM ajustado para opciones sobre divisas, se generan múltiples trayectorias del tipo de cambio hasta la fecha de vencimiento. La fórmula ajustada para el GBM en este caso es:
Luego, aplicar los pasos 3 y 4 anteriormente vistos.
import numpy as np
def valorar_opcion_divisa_call(S0, K, T, rd, rf, sigma, num_simulaciones):
if seed is not None:
np.random.seed(seed) # Establecer la semilla
dt = T # Asumimos un paso de tiempo hasta el vencimiento
Z = np.random.standard_normal(num_simulaciones)
ST = S0 * np.exp((rd - rf - 0.5 * sigma**2) * dt + sigma * np.sqrt(dt) * Z)
payoff = np.maximum(ST - K, 0) # Para Put sería np.maximum(K - ST , 0)
V0 = np.exp(-rd * T) * np.mean(payoff)
return V0
# Parámetros de la opción sobre divisas
S0 = 4000 # Tipo de cambio actual USD/COP
K = 4100 # Precio de ejercicio
T = 1.0 # Tiempo hasta el vencimiento (en años)
rd = 0.10 # Tasa de interés COP expresada cómo Compuesta Continua Anual (CCA)
rf = 0.05 # Tasa de interés USD expresada cómo Compuesta Continua Anual (CCA)
sigma = 0.1 # Volatilidad del tipo de cambio
num_simulaciones = 10000 # Número de simulaciones
seed = 52
precio_opcion = valorar_opcion_divisa_call(S0, K, T, rd, rf, sigma, num_simulaciones)
print("El precio de la opción de compra sobre divisas es:", precio_opcion)
El precio de la opción de compra sobre divisas es: 200.30730440936077
Ejemplo TRM:#
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Leer el archivo CSV, ajustando el formato de los números
df = pd.read_csv("TRM.csv", delimiter=";")
df["Fecha"] = pd.to_datetime(df["Fecha"], format="%d/%m/%Y")
df["Precio"] = (
df["Precio"]
.str.replace(".", "", regex=False)
.str.replace(",", ".", regex=False)
.astype(float)
)
# Calcular los rendimientos logarítmicos para el gráfico
rendimientos_log = np.log(df["Precio"] / df["Precio"].shift(1))
# Crear figuras para los gráficos
fig, ax = plt.subplots(2, 1, figsize=(12, 8))
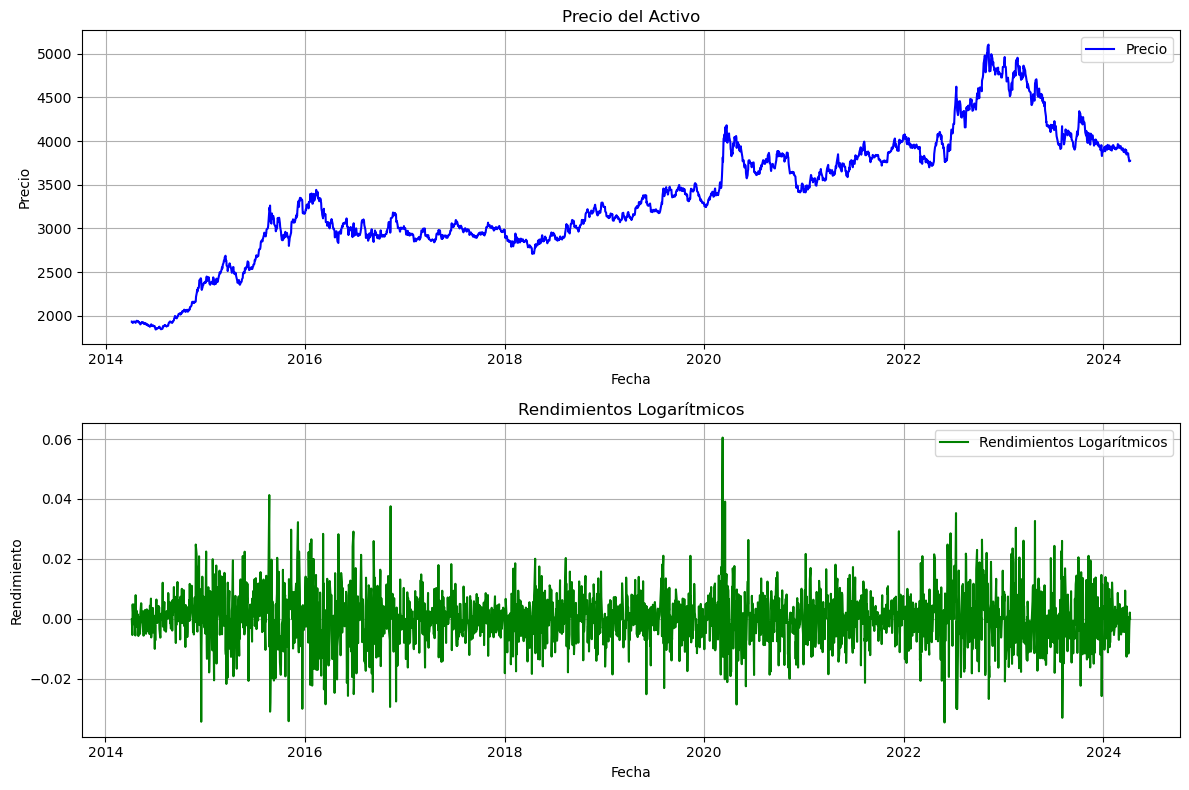
# Gráfico de los precios
ax[0].plot(df["Fecha"], df["Precio"], label="Precio", color="blue")
ax[0].set_title("Precio del Activo")
ax[0].set_xlabel("Fecha")
ax[0].set_ylabel("Precio")
ax[0].legend()
ax[0].grid(True)
# Gráfico de los rendimientos logarítmicos
ax[1].plot(
df["Fecha"], rendimientos_log, label="Rendimientos Logarítmicos", color="green"
)
ax[1].set_title("Rendimientos Logarítmicos")
ax[1].set_xlabel("Fecha")
ax[1].set_ylabel("Rendimiento")
ax[1].legend()
ax[1].grid(True)
plt.tight_layout()
plt.show()
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Cargar los datos desde el archivo CSV, corrigiendo el formato de los números
df = pd.read_csv("TRM.csv", delimiter=";")
df["Fecha"] = pd.to_datetime(df["Fecha"], format="%d/%m/%Y")
df["Precio"] = (
df["Precio"]
.str.replace(".", "", regex=False)
.str.replace(",", ".", regex=False)
.astype(float)
)
# Calcular las tasas de retorno logarítmicas y sus parámetros
precios = df["Precio"].values
tasas_retorno_log = np.log(precios[1:] / precios[:-1])
sigma = tasas_retorno_log.std() # Volatilidad
# Datos de las tasas libres de riesgo:
rd = 0.12121 # E.A. (IBR para 1 mes)
rf = 0.0532999 # Nominal Anual (SOFR para 1 mes)
# Conversión de tasas a CCA.
rd = np.log(1 + rd / 12) / 30 # C.C.D.
rf = np.log(1 + rf / 12) / 30 # C.C.D.
def valorar_opcion_divisa_call(S0, K, T, rd, rf, sigma, num_simulaciones):
if seed is not None:
np.random.seed(seed) # Establecer la semilla
dt = T # Asumimos un paso de tiempo hasta el vencimiento
Z = np.random.standard_normal(num_simulaciones)
ST = S0 * np.exp((rd - rf - 0.5 * sigma**2) * dt + sigma * np.sqrt(dt) * Z)
payoff = np.maximum(ST - K, 0) # Para Put sería np.maximum(K - ST , 0)
V0 = np.exp(-rd * T) * np.mean(payoff)
return V0
# Parámetros de la opción sobre divisas
S0 = df["Precio"].iloc[-1] # Precio inicial: último precio conocido
K = 3700 # Precio de ejercicio
T = 30 # Tiempo hasta el vencimiento (en días)
num_simulaciones = 10000 # Número de simulaciones
seed = 52
precio_opcion = valorar_opcion_divisa_call(S0, K, T, rd, rf, sigma, num_simulaciones)
print("El precio de la opción de compra sobre divisas es:", precio_opcion)
El precio de la opción de compra sobre divisas es: 127.36404555816445