Ajuste modelo AR al precio de electricidad#
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
Funciones:#
def plot_serie_tiempo(
serie: pd.DataFrame,
nombre: str,
unidades: str = None,
columna: str = None,
fecha_inicio: str = None,
fecha_fin: str = None,
color: str = 'navy',
linewidth: float = 2,
num_xticks: int = 12,
estacionalidad: str = None, # 'diciembre', 'enero', 'semana', 'semestre', 'custom_month'
custom_month: int = None, # Si quieres marcar otro mes (ejemplo: 3 para marzo)
vline_label: str = None, # Etiqueta para la(s) línea(s) vertical(es)
hlines: list = None, # lista de valores horizontales a marcar
hlines_labels: list = None, # lista de etiquetas para líneas horizontales
color_estacion: str = 'darkgray', # color de las líneas estacionales
alpha_estacion: float = 0.3, # transparencia de líneas estacionales
color_hline: str = 'gray', # color de las líneas horizontales
alpha_hline: float = 0.7 # transparencia de líneas horizontales
):
"""
Gráfico elegante de serie de tiempo.
- Eje X alineado con la primera fecha real de la serie.
- Opcional: marcar estacionalidades (diciembres, semanas, semestres, mes personalizado) con etiqueta.
- Líneas horizontales con etiqueta opcional (legend).
"""
df = serie.copy()
if columna is None:
columna = df.columns[0]
if fecha_inicio:
df = df[df.index >= fecha_inicio]
if fecha_fin:
df = df[df.index <= fecha_fin]
# Asegura que el índice sea datetime y esté ordenado
df = df.sort_index()
df.index = pd.to_datetime(df.index)
plt.style.use('ggplot')
fig, ax = plt.subplots(figsize=(14, 6))
# Gráfica principal
ax.plot(df.index, df[columna], color=color, linewidth=linewidth, label=nombre)
ax.set_title(f"Serie de tiempo: {nombre}", fontsize=20, weight='bold',
color='black')
ax.set_xlabel("Fecha", fontsize=15, color='black')
ax.set_ylabel(unidades, fontsize=15, color='black')
ax.tick_params(axis='both', colors='black', labelsize=13)
for label in ax.get_xticklabels() + ax.get_yticklabels():
label.set_color('black')
# Limita el rango del eje X exactamente al rango de fechas de la serie (no corrido)
ax.set_xlim(df.index.min(), df.index.max())
# Ticks equidistantes en eje X, asegurando que empieza en la primera fecha
idx = df.index
if len(idx) > num_xticks:
ticks = np.linspace(0, len(idx)-1, num_xticks, dtype=int)
ticks[0] = 0 # asegúrate que arranque en la primera fecha
ticklabels = [idx[i] for i in ticks]
ax.set_xticks(ticklabels)
ax.set_xticklabels([pd.to_datetime(t).strftime('%b %Y') for t in ticklabels], rotation=0, color='black')
else:
ax.xaxis.set_major_formatter(mdates.DateFormatter('%b %Y'))
fig.autofmt_xdate(rotation=0)
# ==============================
# LÍNEAS VERTICALES: Estacionalidad (con etiqueta en leyenda si se desea)
# ==============================
vlines_plotted = False
if estacionalidad is not None:
if estacionalidad == 'diciembre':
fechas_mark = df[df.index.month == 12].index
elif estacionalidad == 'enero':
fechas_mark = df[df.index.month == 1].index
elif estacionalidad == 'semana':
fechas_mark = df[df.index.weekday == 0].index
elif estacionalidad == 'semestre':
fechas_mark = df[df.index.month.isin([6, 12])].index
elif estacionalidad == 'custom_month' and custom_month is not None:
fechas_mark = df[df.index.month == custom_month].index
else:
fechas_mark = []
for i, f in enumerate(fechas_mark):
# Solo pone la etiqueta una vez (la primera línea)
if not vlines_plotted and vline_label is not None:
ax.axvline(f, color=color_estacion, alpha=alpha_estacion, linewidth=2, linestyle='--', zorder=0, label=vline_label)
vlines_plotted = True
else:
ax.axvline(f, color=color_estacion, alpha=alpha_estacion, linewidth=2, linestyle='--', zorder=0)
# ==============================
# LÍNEAS HORIZONTALES OPCIONALES, con leyenda
# ==============================
if hlines is not None:
if hlines_labels is None:
hlines_labels = [None] * len(hlines)
for i, h in enumerate(hlines):
if hlines_labels[i] is not None:
ax.axhline(h, color=color_hline, alpha=alpha_hline, linewidth=1.5, linestyle='--', zorder=0, label=hlines_labels[i])
else:
ax.axhline(h, color=color_hline, alpha=alpha_hline, linewidth=1.5, linestyle='--', zorder=0)
# Coloca la leyenda solo si hay etiquetas
handles, labels = ax.get_legend_handles_labels()
if any(labels):
ax.legend(loc='best', fontsize=13, frameon=True)
ax.grid(True, alpha=0.4)
plt.tight_layout()
plt.show()
##################################################################################
def analisis_estacionariedad(
serie: pd.Series,
nombre: str = None,
lags: int = 24,
xtick_interval: int = 3
):
"""
Gráfica y análisis de estacionariedad para una serie de tiempo:
- Serie original, diferencia, logaritmo y diferencia del logaritmo.
- Muestra la ACF, PACF y resultado ADF en subplots.
Args:
serie: Serie de tiempo (índice datetime, pandas.Series)
nombre: Nombre de la serie (para títulos)
lags: Número de rezagos para ACF/PACF
xtick_interval: Mostrar ticks en X cada este número de lags, incluyendo siempre el lag 1
"""
if nombre is None:
nombre = serie.name if serie.name is not None else "Serie"
# Transformaciones
serie_1 = serie.copy()
serie_2 = serie_1.diff().dropna()
serie_3 = np.log(serie_1)
serie_4 = serie_3.diff().dropna()
titulos = [
f"Serie original: {nombre}",
"Diferenciación",
"Logaritmo",
"Diferenciación del Logaritmo"
]
series = [serie_1, serie_2, serie_3, serie_4]
resultados_adf = []
interpretaciones = []
for i, serie_i in enumerate(series):
serie_ = serie_i.dropna()
# Selección de regresión en ADF
if i in [0, 2]:
adf = adfuller(serie_, regression='ct')
else:
adf = adfuller(serie_, regression='c')
estadistico = adf[0]
pvalue = adf[1]
resultados_adf.append((estadistico, pvalue))
interpretaciones.append("Estacionaria" if pvalue < 0.05 else "No estacionaria")
fig, axes = plt.subplots(4, 3, figsize=(18, 16))
colores = ['black', 'black', 'black', 'black']
for fila in range(4):
# Serie y etiquetas
axes[fila, 0].plot(series[fila], color=colores[fila])
axes[fila, 0].set_title(titulos[fila], color='black')
axes[fila, 0].set_xlabel("Fecha", color='black')
if fila == 0:
axes[fila, 0].set_ylabel("Valor", color='black')
elif fila == 1:
axes[fila, 0].set_ylabel("Δ Valor", color='black')
elif fila == 2:
axes[fila, 0].set_ylabel("Log(Valor)", color='black')
else:
axes[fila, 0].set_ylabel("Δ Log(Valor)", color='black')
axes[fila, 0].grid(True, alpha=0.3)
axes[fila, 0].tick_params(axis='both', labelsize=11, colors='black')
# ACF
plot_acf(
series[fila].dropna(),
lags=lags,
ax=axes[fila, 1],
zero=False,
color=colores[fila]
)
axes[fila, 1].set_title("ACF", color='black')
# xticks: incluir lag 1 y luego cada xtick_interval (ej: 1, 3, 6, ...)
xticks = [1] + list(range(xtick_interval, lags + 1, xtick_interval))
xticks = sorted(set(xticks)) # asegura que no haya duplicados
axes[fila, 1].set_xticks(xticks)
axes[fila, 1].tick_params(axis='both', labelsize=11, colors='black')
axes[fila, 1].set_xlabel("Lag", color='black')
axes[fila, 1].set_ylabel("Autocorrelación", color='black')
# PACF
plot_pacf(
series[fila].dropna(),
lags=lags,
ax=axes[fila, 2],
zero=False,
color=colores[fila]
)
axes[fila, 2].set_title("PACF", color='black')
axes[fila, 2].set_xticks(xticks)
axes[fila, 2].tick_params(axis='both', labelsize=11, colors='black')
axes[fila, 2].set_xlabel("Lag", color='black')
axes[fila, 2].set_ylabel("Autocorrelación parcial", color='black')
# Indicador estacionariedad (más abajo)
axes[fila, 0].text(
0.02, 0.85,
f"ADF: {resultados_adf[fila][0]:.2f}\np-valor: {resultados_adf[fila][1]:.4f}\n{interpretaciones[fila]}",
transform=axes[fila, 0].transAxes,
fontsize=11, bbox=dict(facecolor='white', alpha=0.85), color='black'
)
plt.tight_layout()
plt.show()
# Devuelve los resultados en un dict (opcional)
adf_dict = {
titulos[i]: {
"estadístico ADF": resultados_adf[i][0],
"p-valor": resultados_adf[i][1],
"interpretación": interpretaciones[i]
}
for i in range(4)
}
return adf_dict
Precio de electricidad#
# Cargar el archivo
precio_electricidad = pd.read_csv("Precio_electricidad.csv")
# Corregir nombres de columnas si tienen espacios
precio_electricidad.columns = precio_electricidad.columns.str.strip()
# Convertir 'Fecha' a datetime y usar como índice
precio_electricidad['Fecha'] = pd.to_datetime(precio_electricidad['Fecha'])
precio_electricidad.set_index('Fecha', inplace=True)
# Ordenar por fecha por si acaso
precio_electricidad = precio_electricidad.sort_index()
# Establecer frecuencia explícita para evitar el warning de statsmodels
precio_electricidad.index.freq = precio_electricidad.index.inferred_freq
precio_electricidad.head()
| Precio | |
|---|---|
| Fecha | |
| 2000-01-01 | 36.539729 |
| 2000-02-01 | 39.885205 |
| 2000-03-01 | 35.568126 |
| 2000-04-01 | 44.957443 |
| 2000-05-01 | 33.848903 |
plot_serie_tiempo(
precio_electricidad,
nombre="Precio de electricidad",
columna='Precio',
unidades='COP/kWh',
estacionalidad='diciembre',
vline_label="Diciembre",
num_xticks = 14
)
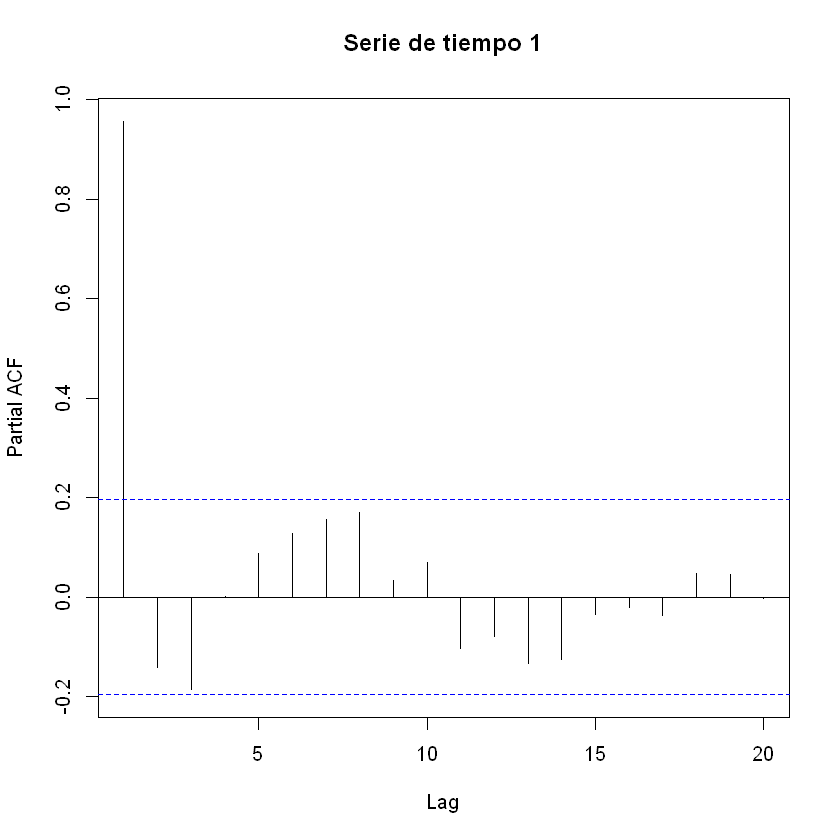
adf_resultados = analisis_estacionariedad(
precio_electricidad['Precio'],
nombre="Precio de electricidad",
lags=36,
xtick_interval=3
)
Modelo AR a la serie transformada: logaritmo#
Serie transformada: logaritmo
# Transformación: Logaritmo
df_log = np.log(precio_electricidad)
plot_serie_tiempo(
df_log,
nombre="Logaritmo del precio de electricidad",
columna='Precio',
unidades='',
num_xticks = 14
)
Conjunto de train y test:
# Dividir en train y test (por ejemplo, 80% train, 20% test)
split = int(len(df_log) * 0.8)
train, test = df_log[:split], df_log[split:]
# Graficar train y test:
plt.figure(figsize=(12, 5))
plt.plot(train, label='Train', color='navy')
plt.plot(test, label='Test', color='orange')
plt.title("Conjunto de train y test")
plt.xlabel("Fecha")
plt.ylabel("Valor")
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
SARIMAX de statsmodels:
El parámetro order en la función SARIMAX se utiliza para definir
la estructura del modelo.
Cuando queremos ajustar únicamente la parte autorregresiva (AR) de un modelo, nos enfocamos en el primer valor del parámetro:
order = (p, d, q)
p: número de rezagos autorregresivos (AR)
d:diferenciaciones aplicadas a la serie (para AR puro, d = 0).
Número de veces que se diferencia la serie para hacerla estacionaria en
media. Sirve para eliminar tendencias.
q: número de rezagos de la media móvil (para AR puro, q = 0)
Para un modelo AR puro, se utiliza:
order = (p, 0, 0)
El parámetro trend permite incluir una tendencia determinística
dentro del modelo.
Controla si se incorpora un intercepto o una tendencia lineal en la ecuación.
Opciones más comunes:
Valor |
Descripción |
Ecuación del modelo resultante |
|---|---|---|
|
Sin constante ni tendencia |
\(y_t = \sum_{i =1}^{p} \phi_i y_{t-i} + \varepsilon_t\) |
|
Con constante (intercepto) |
\(y_t = \alpha + \sum_{i =1}^{p} \phi_i y_{t-i} + \varepsilon_t\) |
|
Con tendencia lineal (sin intercepto) |
\(y_t = \beta_t + \sum_{i =1}^{p} \phi_i y_{t-i} + \varepsilon_t\) |
` ‘ct’` |
Constante + tendencia lineal |
\(y_t = \alpha + \beta_t + \sum_{i =1}^{p} \phi_i y_{t-i} + \varepsilon_t\) |
donde:
\(\alpha\) representa la constante (intercepto),
\(\beta_t\) es la tendencia lineal en el tiempo,
\(\phi_i\) son los coeficientes autorregresivos,
\(\varepsilon_t\) es el término de error (ruido blanco).
Cuándo usar cada uno
'n'→ cuando la serie ya fue centrada (media cero) o diferenciada.'c'→ cuando la serie es estacionaria pero tiene media distinta de cero (opción más común).'t'→ cuando la serie muestra tendencia lineal pero se asume sin nivel promedio fijo.'ct'→ cuando existe una tendencia lineal y un nivel medio.
Ajuste modelo AR#
from statsmodels.tsa.statespace.sarimax import SARIMAX
# Definir los parámetros del modelo AR (p, 0, 0)
order = (1, 0, 0) # Puedes ajustar según el análisis de ACF y PACF
trend = 'ct' # 'c' = constante, 't' = tendencia, 'ct' = constante + tendencia, 'n' = sin tendencia
# Ajustar el modelo con los datos de entrenamiento
model = SARIMAX(train, order=order, trend=trend)
results = model.fit()
# Mostrar resumen del modelo
print(results.summary())
SARIMAX Results
==============================================================================
Dep. Variable: Precio No. Observations: 232
Model: SARIMAX(1, 0, 0) Log Likelihood -7.218
Date: Fri, 17 Oct 2025 AIC 22.436
Time: 14:03:03 BIC 36.223
Sample: 01-01-2000 HQIC 27.996
- 04-01-2019
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
intercept 0.6807 0.122 5.600 0.000 0.442 0.919
drift 0.0012 0.000 3.282 0.001 0.000 0.002
ar.L1 0.8251 0.030 27.572 0.000 0.766 0.884
sigma2 0.0621 0.004 14.777 0.000 0.054 0.070
===================================================================================
Ljung-Box (L1) (Q): 0.81 Jarque-Bera (JB): 54.71
Prob(Q): 0.37 Prob(JB): 0.00
Heteroskedasticity (H): 4.41 Skew: 0.51
Prob(H) (two-sided): 0.00 Kurtosis: 5.15
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
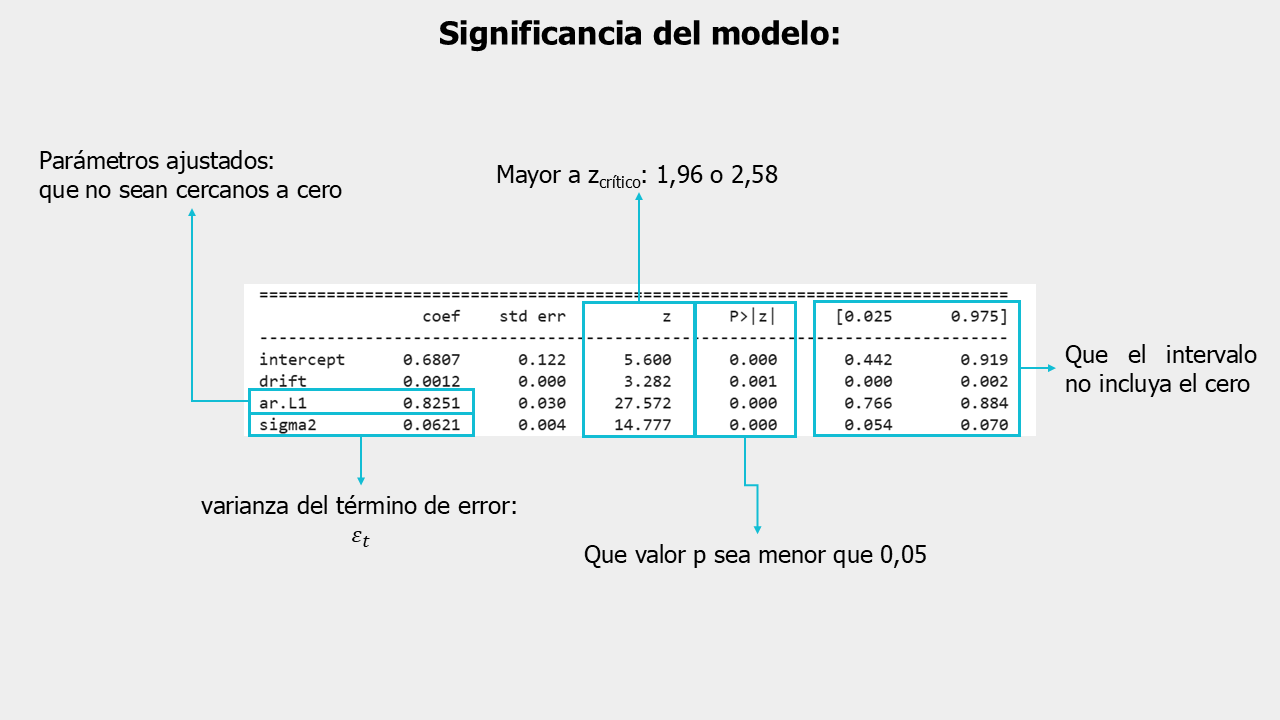
Significancia#
Cómo determinar la significancia:
Revisar el valor p (P>|z|):
\(p < 0.05\) → el parámetro es significativo.
\(p \ge 0.05\) → no hay evidencia suficiente.
Verificar el intervalo de confianza:
Si no incluye cero, el parámetro también es significativo.
Analizar el signo y magnitud del coeficiente:
Positivo → relación directa con el rezago.
Negativo → relación inversa (efecto de rebote).
Entre más bajo sea std err, mejor.
Pronóstico modelo AR#
Ajuste en train#
Pronóstico dentro de la muestra (in-sample):
###### Pronóstico dentro de la muestra (train) ######
fitted_values = results.fittedvalues
conf_int_train = results.get_prediction().conf_int(alpha=0.05) # Intervalo de confianza del 95%
# Alinear por si el índice de train y fitted_values difieren en los primeros p rezagos
fitted_values = fitted_values.reindex(train.index)
##### Gráfico #####
plt.figure(figsize=(12, 6))
# Train y fitted
plt.plot(train[1:], label='Train', color='black')
plt.plot(fitted_values[1:], label='Ajuste en Train', color='tab:blue')
# Banda de confianza en train
plt.fill_between(conf_int_train[1:].index,
conf_int_train.iloc[1:, 0],
conf_int_train.iloc[1:, 1],
color='tab:blue', alpha=0.2, label='IC 95% - train')
plt.title('Ajuste y pronóstico')
plt.xlabel('Tiempo')
plt.ylabel('Log(Valor)')
plt.legend()
plt.tight_layout()
plt.show()
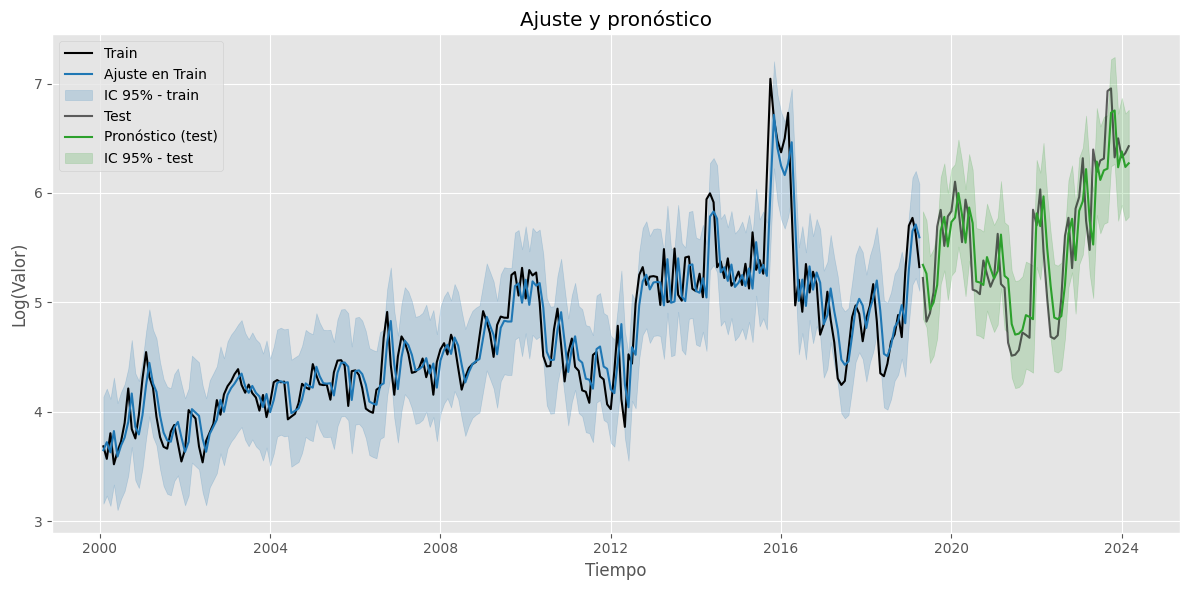
Pronóstico en test#
Pronóstico fuera de la muestra (out-sample) - test:
###### Pronóstico fuera de la muestra (test) #####
current_results = results # Modelo ajustado
forecasted_test = []
lower_ci_test = []
upper_ci_test = []
for i in range(len(test)):
forecaster = current_results.get_forecast(steps=1) # Un pronóstico hacia adelante
forecast_mean_test = forecaster.predicted_mean.iloc[0] # Media del pronóstico
ci_i_test = forecaster.conf_int(alpha=0.05).iloc[0] # Intervalo de confianza del 95%
forecasted_test.append(forecast_mean_test)
lower_ci_test.append(ci_i_test.iloc[0]) # límite inferior
upper_ci_test.append(ci_i_test.iloc[1]) # límite superior
# Actualiza el estado con el valor real (método recursivo)
current_results = current_results.append(endog=[test.iloc[i]], refit=False)
forecasted_test = pd.Series(forecasted_test, index=test.index, name='forecast_test')
lower_ci_test = pd.Series(lower_ci_test, index=test.index, name='lower_test')
upper_ci_test = pd.Series(upper_ci_test, index=test.index, name='upper_test')
##### Gráfico #####
plt.figure(figsize=(12, 6))
# Train y fitted
plt.plot(train[1:], label='Train', color='black')
plt.plot(fitted_values[1:], label='Ajuste en Train', color='tab:blue')
# Banda de confianza en train
plt.fill_between(conf_int_train[1:].index,
conf_int_train.iloc[1:, 0],
conf_int_train.iloc[1:, 1],
color='tab:blue', alpha=0.2, label='IC 95% - train')
# Test y forecast
plt.plot(test, label='Test', color='black', alpha=0.6)
plt.plot(test.index, forecasted_test, label='Pronóstico (test)', color='tab:green')
# Banda de confianza en test
plt.fill_between(lower_ci_test.index,
lower_ci_test,
upper_ci_test,
color='tab:green', alpha=0.2, label='IC 95% - test')
plt.title('Ajuste y pronóstico')
plt.xlabel('Tiempo')
plt.ylabel('Log(Valor)')
plt.legend()
plt.tight_layout()
plt.show()
Pronóstico fuera de la muestra#
Pronóstico fechas futuras:
###### Pronóstico fuera de la muestra: futuro #####
n_forecast = 12 # Pronóstico para 12 meses
# Actualiza el estado con el dataset de test
current_results = results.append(endog=test, refit=False)
forecasting = []
lower_ci = []
upper_ci = []
for i in range(n_forecast):
forecaster = current_results.get_forecast(steps=1) # Un pronóstico hacia adelante
forecast_mean = forecaster.predicted_mean.iloc[0] # Media del pronóstico
ci_i = forecaster.conf_int(alpha=0.05).iloc[0] # Intervalo de confianza del 95%
forecasting.append(forecast_mean)
lower_ci.append(ci_i.iloc[0]) # límite inferior
upper_ci.append(ci_i.iloc[1]) # límite superior
# Alimenta el modelo con el valor pronosticado (pronóstico puro hacia adelante)
current_results = current_results.append(endog=[forecast_mean], refit=False)
# Fechas futuras (mensuales inicio de mes)
last_date = test.index[-1]
future_dates = pd.date_range(start=last_date + pd.offsets.MonthBegin(1),
periods=n_forecast, freq='MS')
# Asegura Series con índice de fechas
forecasting = pd.Series(forecasting, index=future_dates, name='forecast')
lower_ci = pd.Series(lower_ci, index=future_dates, name='lower')
upper_ci = pd.Series(upper_ci, index=future_dates, name='upper')
##### Gráfico #####
plt.figure(figsize=(12, 6))
# Train y fitted
plt.plot(train[1:], label='Train', color='black')
plt.plot(fitted_values[1:], label='Ajuste en Train', color='tab:blue')
# Banda de confianza en train
plt.fill_between(conf_int_train[1:].index,
conf_int_train.iloc[1:, 0],
conf_int_train.iloc[1:, 1],
color='tab:blue', alpha=0.2, label='IC 95% - train')
# Test y forecast
plt.plot(test, label='Test', color='black', alpha=0.6)
plt.plot(test.index, forecasted_test, label='Pronóstico (test)', color='tab:green')
# Banda de confianza en test
plt.fill_between(lower_ci_test.index,
lower_ci_test,
upper_ci_test,
color='tab:green', alpha=0.2, label='IC 95% - test')
plt.plot(forecasting, label='Pronóstico (12 meses)', color='tab:red')
# Banda de confianza
plt.fill_between(future_dates,
lower_ci.values,
upper_ci.values,
color='tab:red', alpha=0.2, label='IC 95% - pronóstico')
plt.title('Ajuste y pronóstico')
plt.xlabel('Tiempo')
plt.ylabel('Log(Valor)')
plt.legend()
plt.tight_layout()
plt.show()
Resumen código ajuste y pronóstico#
###### Pronóstico dentro de la muestra (train) ######
fitted_values = results.fittedvalues
conf_int_train = results.get_prediction().conf_int(alpha=0.05) # Intervalo de confianza del 95%
# Alinear por si el índice de train y fitted_values difieren en los primeros p rezagos
fitted_values = fitted_values.reindex(train.index)
###### Pronóstico fuera de la muestra (test) #####
current_results = results # Modelo ajustado
forecasted_test = []
lower_ci_test = []
upper_ci_test = []
for i in range(len(test)):
forecaster = current_results.get_forecast(steps=1) # Un pronóstico hacia adelante
forecast_mean_test = forecaster.predicted_mean.iloc[0] # Media del pronóstico
ci_i_test = forecaster.conf_int(alpha=0.05).iloc[0] # Intervalo de confianza del 95%
forecasted_test.append(forecast_mean_test)
lower_ci_test.append(ci_i_test.iloc[0]) # límite inferior
upper_ci_test.append(ci_i_test.iloc[1]) # límite superior
# Actualiza el estado con el valor real (método recursivo)
current_results = current_results.append(endog=[test.iloc[i]], refit=False)
forecasted_test = pd.Series(forecasted_test, index=test.index, name='forecast_test')
lower_ci_test = pd.Series(lower_ci_test, index=test.index, name='lower_test')
upper_ci_test = pd.Series(upper_ci_test, index=test.index, name='upper_test')
###### Pronóstico fuera de la muestra: futuro #####
n_forecast = 12 # Pronóstico para 12 meses
# Actualiza el estado con el dataset de test
current_results = results.append(endog=test, refit=False)
forecasting = []
lower_ci = []
upper_ci = []
for i in range(n_forecast):
forecaster = current_results.get_forecast(steps=1) # Un pronóstico hacia adelante
forecast_mean = forecaster.predicted_mean.iloc[0] # Media del pronóstico
ci_i = forecaster.conf_int(alpha=0.05).iloc[0] # Intervalo de confianza del 95%
forecasting.append(forecast_mean)
lower_ci.append(ci_i.iloc[0]) # límite inferior
upper_ci.append(ci_i.iloc[1]) # límite superior
# Alimenta el modelo con el valor pronosticado (pronóstico puro hacia adelante)
current_results = current_results.append(endog=[forecast_mean], refit=False)
# Fechas futuras (mensuales inicio de mes)
last_date = test.index[-1]
future_dates = pd.date_range(start=last_date + pd.offsets.MonthBegin(1),
periods=n_forecast, freq='MS')
# Asegura Series con índice de fechas
forecasting = pd.Series(forecasting, index=future_dates, name='forecast')
lower_ci = pd.Series(lower_ci, index=future_dates, name='lower')
upper_ci = pd.Series(upper_ci, index=future_dates, name='upper')
##### Gráfico #####
plt.figure(figsize=(12, 6))
# Train y fitted
plt.plot(train[1:], label='Train', color='black')
plt.plot(fitted_values[1:], label='Ajuste en Train', color='tab:blue')
# Banda de confianza en train
plt.fill_between(conf_int_train[1:].index,
conf_int_train.iloc[1:, 0],
conf_int_train.iloc[1:, 1],
color='tab:blue', alpha=0.2, label='IC 95% - train')
# Test y forecast
plt.plot(test, label='Test', color='black', alpha=0.6)
plt.plot(test.index, forecasted_test, label='Pronóstico (test)', color='tab:green')
# Banda de confianza en test
plt.fill_between(lower_ci_test.index,
lower_ci_test,
upper_ci_test,
color='tab:green', alpha=0.2, label='IC 95% - test')
plt.plot(forecasting, label='Pronóstico (12 meses)', color='tab:red')
# Banda de confianza
plt.fill_between(future_dates,
lower_ci.values,
upper_ci.values,
color='tab:red', alpha=0.2, label='IC 95% - pronóstico')
plt.title('Ajuste y pronóstico')
plt.xlabel('Tiempo')
plt.ylabel('Log(Valor)')
plt.legend()
plt.tight_layout()
plt.show()
Evaluación del desempeño#
from sklearn.metrics import mean_squared_error, r2_score
# --- Métricas en el conjunto de entrenamiento ---
# Ignoramos el primer valor (índice 0) porque no tiene fitted válido
mse_train = mean_squared_error(train[1:], fitted_values[1:])
r2_train = r2_score(train[1:], fitted_values[1:])
# --- Métricas en el conjunto de prueba (pronóstico recursivo) ---
mse_test = mean_squared_error(test, forecasted_test)
r2_test = r2_score(test, forecasted_test)
print("📈 Desempeño del modelo AR")
print("-" * 40)
print(f"MSE (Train): {mse_train:.4f}")
print(f"R² (Train): {r2_train:.4f}")
print()
print(f"MSE (Test) : {mse_test:.4f}")
print(f"R² (Test) : {r2_test:.4f}")
📈 Desempeño del modelo AR
----------------------------------------
MSE (Train): 0.0621
R² (Train): 0.8463
MSE (Test) : 0.1201
R² (Test) : 0.6963
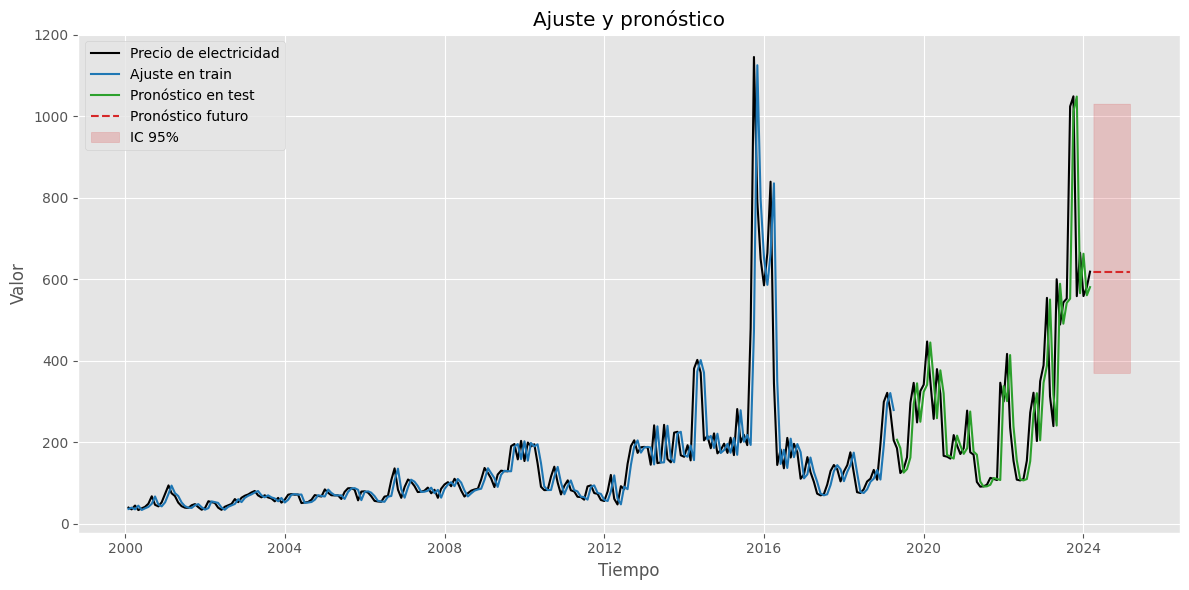
Resultados sobre la serie original:#
# Inversa de la transformación
y_pred_train = np.exp(fitted_values)
y_pred_test = np.exp(forecasted_test)
forcasting_orig = np.exp(forecasting) # pronóstico futuro
# Intervalos de confianza
lower_bt = np.exp(lower_ci)
upper_bt = np.exp(upper_ci)
# Graficar sobre la serie original
plt.figure(figsize=(12,6))
# Serie original
plt.plot(precio_electricidad[1:], label='Precio de electricidad', color='black')
# Ajuste en train
plt.plot(y_pred_train[1:], label='Ajuste en train', color='tab:blue')
# Ajuste en test
plt.plot(y_pred_test, label='Pronóstico en test', color='tab:green')
# Pronóstico futuro + IC
plt.plot(forcasting_orig, label='Pronóstico futuro', color='tab:red', linestyle='--')
plt.fill_between(future_dates, lower_bt.values, upper_bt.values, color='tab:red', alpha=0.2, label='IC 95%')
plt.title('Ajuste y pronóstico')
plt.xlabel('Tiempo')
plt.ylabel('Valor')
plt.legend()
plt.tight_layout()
plt.show()
Modelo AR a la serie transformada: diferencia del logaritmo#
Ajuste:
Anteriormnete la serie fue transformada aplicando logaritmo, para aplicar luego la diferenciación solo es indicar d=1.
# Definir los parámetros del modelo AR (p, 1, 0) -- d=1
order = (1, 1, 0) # Puedes ajustar según el análisis de ACF y PACF
trend = 'n' # 'c' = constante, 't' = tendencia, 'ct' = constante + tendencia, 'n' = sin tendencia
# Ajustar el modelo con los datos de entrenamiento
model = SARIMAX(train, order=order, trend=trend)
results = model.fit()
# Mostrar resumen del modelo
print(results.summary())
SARIMAX Results
==============================================================================
Dep. Variable: Precio No. Observations: 232
Model: SARIMAX(1, 1, 0) Log Likelihood -17.542
Date: Fri, 17 Oct 2025 AIC 39.085
Time: 14:03:19 BIC 45.970
Sample: 01-01-2000 HQIC 41.862
- 04-01-2019
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 -0.0206 0.046 -0.447 0.655 -0.111 0.070
sigma2 0.0682 0.005 14.415 0.000 0.059 0.077
===================================================================================
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 28.44
Prob(Q): 0.95 Prob(JB): 0.00
Heteroskedasticity (H): 4.24 Skew: 0.16
Prob(H) (two-sided): 0.00 Kurtosis: 4.69
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
No hay significancia:
Coeficiente cercano a cero.
Valor \(|z_i|\) menor a 1,96 o 2,58.
Valor p mayor que 0,05.
El intervalo de significancia incluye el cero.
###### Pronóstico dentro de la muestra (train) ######
fitted_values = results.fittedvalues
conf_int_train = results.get_prediction().conf_int(alpha=0.05) # Intervalo de confianza del 95%
# Alinear por si el índice de train y fitted_values difieren en los primeros p rezagos
fitted_values = fitted_values.reindex(train.index)
###### Pronóstico fuera de la muestra (test) #####
current_results = results # Modelo ajustado
forecasted_test = []
lower_ci_test = []
upper_ci_test = []
for i in range(len(test)):
forecaster = current_results.get_forecast(steps=1) # Un pronóstico hacia adelante
forecast_mean_test = forecaster.predicted_mean.iloc[0] # Media del pronóstico
ci_i_test = forecaster.conf_int(alpha=0.05).iloc[0] # Intervalo de confianza del 95%
forecasted_test.append(forecast_mean_test)
lower_ci_test.append(ci_i_test.iloc[0]) # límite inferior
upper_ci_test.append(ci_i_test.iloc[1]) # límite superior
# Actualiza el estado con el valor real (método recursivo)
current_results = current_results.append(endog=[test.iloc[i]], refit=False)
forecasted_test = pd.Series(forecasted_test, index=test.index, name='forecast_test')
lower_ci_test = pd.Series(lower_ci_test, index=test.index, name='lower_test')
upper_ci_test = pd.Series(upper_ci_test, index=test.index, name='upper_test')
###### Pronóstico fuera de la muestra: futuro #####
n_forecast = 12 # Pronóstico para 12 meses
# Actualiza el estado con el dataset de test
current_results = results.append(endog=test, refit=False)
forecasting = []
lower_ci = []
upper_ci = []
for i in range(n_forecast):
forecaster = current_results.get_forecast(steps=1) # Un pronóstico hacia adelante
forecast_mean = forecaster.predicted_mean.iloc[0] # Media del pronóstico
ci_i = forecaster.conf_int(alpha=0.05).iloc[0] # Intervalo de confianza del 95%
forecasting.append(forecast_mean)
lower_ci.append(ci_i.iloc[0]) # límite inferior
upper_ci.append(ci_i.iloc[1]) # límite superior
# Alimenta el modelo con el valor pronosticado (pronóstico puro hacia adelante)
current_results = current_results.append(endog=[forecast_mean], refit=False)
# Fechas futuras (mensuales inicio de mes)
last_date = test.index[-1]
future_dates = pd.date_range(start=last_date + pd.offsets.MonthBegin(1),
periods=n_forecast, freq='MS')
# Asegura Series con índice de fechas
forecasting = pd.Series(forecasting, index=future_dates, name='forecast')
lower_ci = pd.Series(lower_ci, index=future_dates, name='lower')
upper_ci = pd.Series(upper_ci, index=future_dates, name='upper')
# Inversa de la transformación - SARIMAX devuelve automáticamente la diferenciación
y_pred_train = np.exp(fitted_values)
y_pred_test = np.exp(forecasted_test)
forcasting_orig = np.exp(forecasting) # pronóstico futuro
# Intervalos de confianza
lower_bt = np.exp(lower_ci)
upper_bt = np.exp(upper_ci)
# Graficar sobre la serie original
plt.figure(figsize=(12,6))
# Serie original
plt.plot(precio_electricidad[1:], label='Precio de electricidad', color='black')
# Ajuste en train
plt.plot(y_pred_train[1:], label='Ajuste en train', color='tab:blue')
# Ajuste en test
plt.plot(y_pred_test, label='Pronóstico en test', color='tab:green')
# Pronóstico futuro + IC
plt.plot(forcasting_orig, label='Pronóstico futuro', color='tab:red', linestyle='--')
plt.fill_between(future_dates, lower_bt.values, upper_bt.values, color='tab:red', alpha=0.2, label='IC 95%')
plt.title('Ajuste y pronóstico')
plt.xlabel('Tiempo')
plt.ylabel('Valor')
plt.legend()
plt.tight_layout()
plt.show()