Métodos de Deep Learnign serie irradiancia

Contents

Métodos de Deep Learnign serie irradiancia#

# Importar librerías:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from keras.models import Sequential, load_model
from keras.layers import Dense, Input, Dropout, LSTM, Conv1D, MaxPooling1D, Flatten, TimeDistributed
from keras.layers import SimpleRNN as RNN
from keras import optimizers
from sklearn.metrics import mean_squared_error, r2_score
from scipy.stats import shapiro, kstest, normaltest

# warning
import warnings
warnings.filterwarnings("ignore")

# Cargar datos:
data = pd.read_csv("Irradiance_mensual.csv")
data.index = pd.to_datetime(data['AñoMes'])
data.drop('AñoMes', axis=1, inplace=True)
print(data.head())
plt.figure(figsize=(15,5))
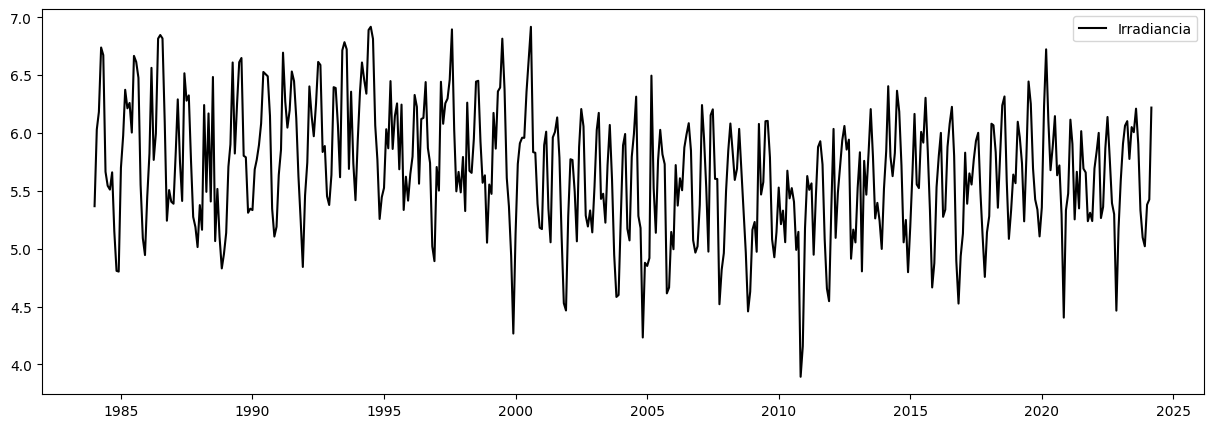
plt.plot(data['Promedio_Irradiacion'], color="black", label="Irradiancia")
plt.legend()
plt.show()

            Promedio_Irradiacion
AñoMes
1984-01-01              5.367742
1984-02-01              6.030690
1984-03-01              6.182903
1984-04-01              6.739667
1984-05-01              6.674194

../../../_images/output_2_17.png

# Funciones:
# Función para crear los lags con entradas los valores y la cantidad de lags:
def prepare_data(precio, n_lags):
    X = []
    y = []
    for i in range(n_lags, len(precio)):

        lag_features = precio[i - n_lags : i, 0]  # Extraemos el vector de lags
        X.append(lag_features)
        # El target es el valor en la posición actual
        y.append(precio[i, 0])

    # Convertimos las listas a numpy.ndarray
    X = np.array(X)
    y = np.array(y)

    return X, y

# Conjunto de Train y Test:
train, test = train_test_split(data, test_size=0.30, shuffle=False)
# Escalado de variables:
scaler = MinMaxScaler()
scaler.fit(train)
train_scaled = scaler.transform(train)
test_scaled = scaler.transform(test)
# Creación de lags:
lags = 3
X_train, y_train = prepare_data(train_scaled, lags)
X_test, y_test = prepare_data(test_scaled, lags)

X_train[:2]

array([[0.48740815, 0.70646554, 0.75676137],
       [0.70646554, 0.75676137, 0.94073235]])

X_train.shape

(335, 3)

MLP:#

# Red Neuronal Artificial Feedforward:

# Creación de lags:
lags = 12
X_train, y_train = prepare_data(train_scaled, lags)
X_test, y_test = prepare_data(test_scaled, lags)

# Hiperparámetros:
units = 20
n_hidden = 2
activation = "relu"
lr = 0.001
epochs = 50
batch_size = 32

# Creación de la red:
model = Sequential()
model.add(Input(shape=(lags,)))

for _ in range(n_hidden):
  model.add(Dense(units, activation=activation))

model.add(Dense(1))

model.compile(optimizer=optimizers.Adam(learning_rate=lr), loss="mse")

history = model.fit(X_train, y_train,
                    validation_data=(X_test, y_test),
                    epochs=epochs,
                    batch_size=batch_size,
                    verbose=0)

# Gráfico de Loss y Val_loss:
plt.figure(figsize=(8,4))
plt.plot(history.history["loss"], label="Loss")
plt.plot(history.history["val_loss"], label="Val_loss")
plt.legend()
plt.show()

# Evaluación del modelo:
y_train_pred = model.predict(X_train, verbose=0)
y_test_pred = model.predict(X_test, verbose=0)

# Graficar y_train y_train_pred:
plt.figure(figsize=(15,5))
plt.plot(train.iloc[lags:].index, y_train, label="y_train", color="blue")
plt.plot(train.iloc[lags:].index, y_train_pred, label="y_train_pred", color="darkred")
plt.plot(test.iloc[lags:].index, y_test, label="y_test", color="green")
plt.plot(test.iloc[lags:].index, y_test_pred, label="y_test_pred", color="darkred")
plt.legend()
plt.show()

# Evaluar el modelo con MSE y R cuadrado:
mse_train = mean_squared_error(y_train, y_train_pred)
mse_test = mean_squared_error(y_test, y_test_pred)
r2_train = r2_score(y_train, y_train_pred)
r2_test = r2_score(y_test, y_test_pred)
print("MSE Train: ", mse_train)
print("MSE Test: ", mse_test)
print("R2 Train: ", r2_train)
print("R2 Test: ", r2_test)

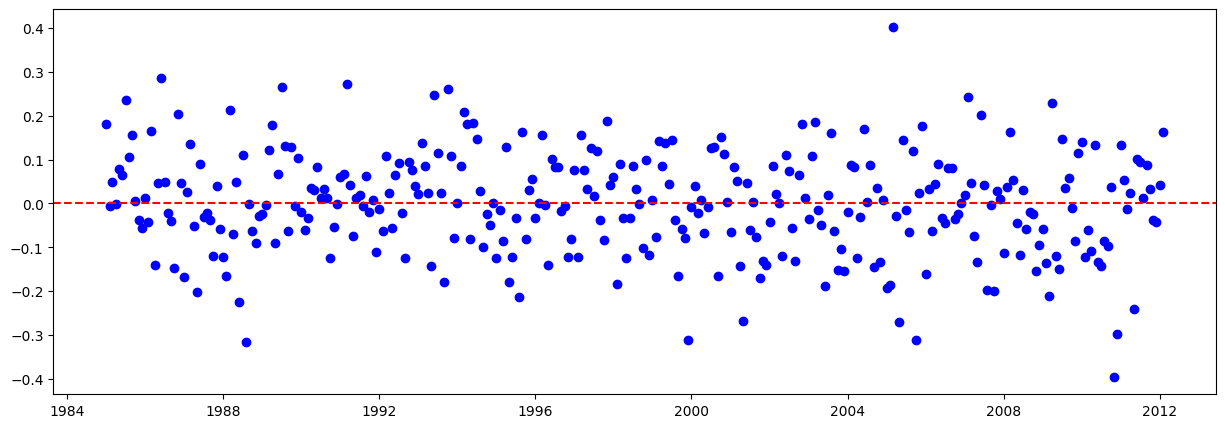
# Graficar los residuales:
residuales = y_train - y_train_pred.flatten()
plt.figure(figsize=(15,5))
plt.scatter(train.iloc[lags:].index, residuales, color="blue")
plt.axhline(y=0, color="red", linestyle="--")
plt.show()
normaltest_result = normaltest(residuales)
shapiro_result = shapiro(residuales)
ks_result = kstest(residuales, "norm")

print("(D'Agostino's K^2):")
if normaltest_result.pvalue < 0.05:
    print("Los residuos NO siguen una distribución normal.")
else:
    print("Los residuos siguen una distribución normal.")
print("")

print("Shapiro-Wilk:")
if shapiro_result.pvalue < 0.05:
    print("Los residuos NO siguen una distribución normal.")
else:
    print("Los residuos siguen una distribución normal.")
print("")

print("Kolmogorov-Smirnov:")
if ks_result.pvalue < 0.05:
    print("Los residuos NO siguen una distribución normal.")
else:
    print("Los residuos siguen una distribución normal.")

../../../_images/output_8_07.png

../../../_images/output_8_14.png

MSE Train:  0.013620000472965436
MSE Test:  0.010071694282748837
R2 Train:  0.6177842224777115
R2 Test:  0.5351821180599243

../../../_images/output_8_3.png

(D'Agostino's K^2):
Los residuos siguen una distribución normal.

Shapiro-Wilk:
Los residuos siguen una distribución normal.

Kolmogorov-Smirnov:
Los residuos NO siguen una distribución normal.

Red Neuronal Recurrente (RNN):#

# Función para crear los lags con entradas los valores y la cantidad de lags:
def prepare_data_rnn(precio, n_lags):
    X = []
    y = []
    for i in range(n_lags, len(precio)):

        lag_features = precio[i - n_lags : i, 0]  # Extraemos el vector de lags
        X.append(lag_features)
        # El target es el valor en la posición actual
        y.append(precio[i, 0])

    # Convertimos las listas a numpy.ndarray
    X = np.array(X)
    y = np.array(y)
    X = X.reshape(X.shape[0], n_lags, 1)

    return X, y

# Creación de lags:
lags = 3
X_train, y_train = prepare_data_rnn(train_scaled, lags)
X_test, y_test = prepare_data_rnn(test_scaled, lags)

X_train.shape

(335, 3, 1)

# Red Neuronal Recurrente:

# Creación de lags:
lags = 12
X_train, y_train = prepare_data_rnn(train_scaled, lags)
X_test, y_test = prepare_data_rnn(test_scaled, lags)

# Hiperparámetros:
units = 20
n_hidden = 2
activation = "relu"
lr = 0.001
epochs = 50
batch_size = 32

# Creación de la red:
model = Sequential()
model.add(Input(shape=(lags,1)))  # Para RNN, GRU, LSTM, input debe ser 3D

for layer in range(n_hidden):
  if layer == n_hidden - 1:
    # Si es la última capa RNN: return_sequences=False
    model.add(RNN(units, activation=activation, return_sequences=False))
  else:
    # Si no es la última capa RNN: return_sequences=True
    model.add(RNN(units, activation=activation, return_sequences=True))

model.add(Dense(1))

model.compile(optimizer=optimizers.Adam(learning_rate=lr), loss="mse")

history = model.fit(X_train, y_train,
                    validation_data=(X_test, y_test),
                    epochs=epochs,
                    batch_size=batch_size,
                    verbose=0)

# Gráfico de Loss y Val_loss:
plt.figure(figsize=(8,4))
plt.plot(history.history["loss"], label="Loss")
plt.plot(history.history["val_loss"], label="Val_loss")
plt.legend()
plt.show()

# Evaluación del modelo:
y_train_pred = model.predict(X_train, verbose=0)
y_test_pred = model.predict(X_test, verbose=0)

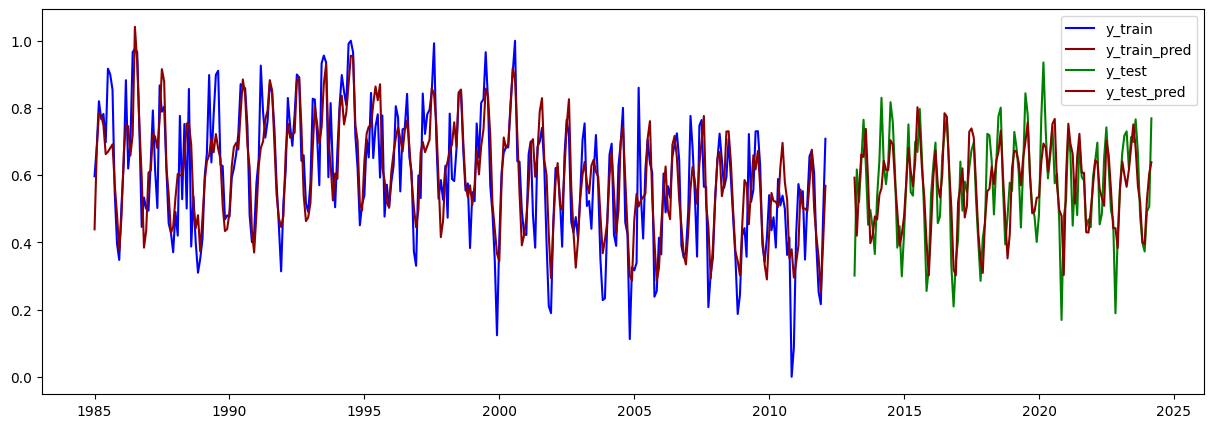
# Graficar y_train y_train_pred:
plt.figure(figsize=(15,5))
plt.plot(train.iloc[lags:].index, y_train, label="y_train", color="blue")
plt.plot(train.iloc[lags:].index, y_train_pred, label="y_train_pred", color="darkred")
plt.plot(test.iloc[lags:].index, y_test, label="y_test", color="green")
plt.plot(test.iloc[lags:].index, y_test_pred, label="y_test_pred", color="darkred")
plt.legend()
plt.show()

# Evaluar el modelo con MSE y R cuadrado:
mse_train = mean_squared_error(y_train, y_train_pred)
mse_test = mean_squared_error(y_test, y_test_pred)
r2_train = r2_score(y_train, y_train_pred)
r2_test = r2_score(y_test, y_test_pred)
print("MSE Train: ", mse_train)
print("MSE Test: ", mse_test)
print("R2 Train: ", r2_train)
print("R2 Test: ", r2_test)

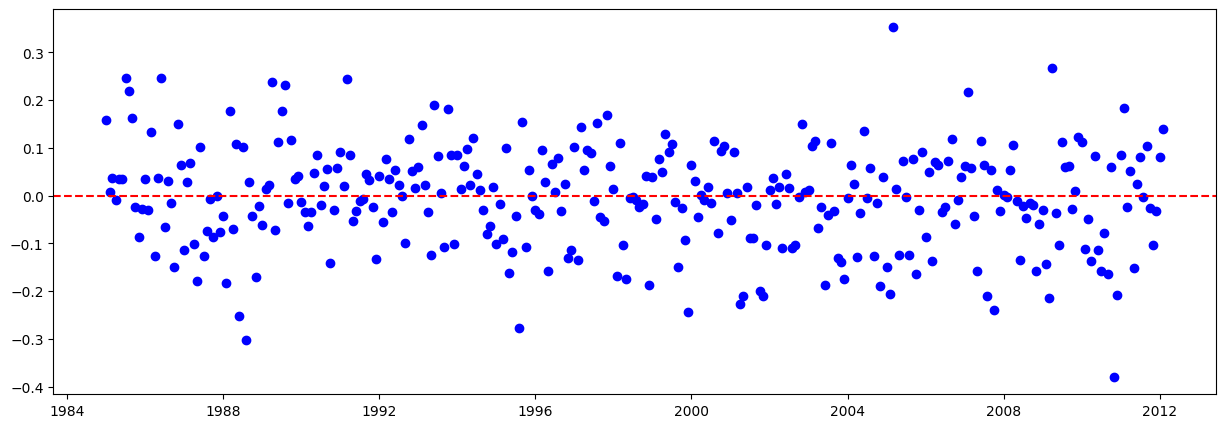
# Graficar los residuales:
residuales = y_train - y_train_pred.flatten()
plt.figure(figsize=(15,5))
plt.scatter(train.iloc[lags:].index, residuales, color="blue")
plt.axhline(y=0, color="red", linestyle="--")
plt.show()
normaltest_result = normaltest(residuales)
shapiro_result = shapiro(residuales)
ks_result = kstest(residuales, "norm")

print("(D'Agostino's K^2):")
if normaltest_result.pvalue < 0.05:
    print("Los residuos NO siguen una distribución normal.")
else:
    print("Los residuos siguen una distribución normal.")
print("")

print("Shapiro-Wilk:")
if shapiro_result.pvalue < 0.05:
    print("Los residuos NO siguen una distribución normal.")
else:
    print("Los residuos siguen una distribución normal.")
print("")

print("Kolmogorov-Smirnov:")
if ks_result.pvalue < 0.05:
    print("Los residuos NO siguen una distribución normal.")
else:
    print("Los residuos siguen una distribución normal.")

../../../_images/output_12_07.png

../../../_images/output_12_15.png

MSE Train:  0.011443827361395383
MSE Test:  0.009640102229048207
R2 Train:  0.6788538016978323
R2 Test:  0.5551004851818204

../../../_images/output_12_3.png

(D'Agostino's K^2):
Los residuos siguen una distribución normal.

Shapiro-Wilk:
Los residuos siguen una distribución normal.

Kolmogorov-Smirnov:
Los residuos NO siguen una distribución normal.

LSTM:#

# Red LSTM:

# Creación de lags:
lags = 12
X_train, y_train = prepare_data_rnn(train_scaled, lags)
X_test, y_test = prepare_data_rnn(test_scaled, lags)

# Hiperparámetros:
units = 20
n_hidden = 2
activation = "relu"
lr = 0.001
epochs = 50
batch_size = 32

# Creación de la red:
model = Sequential()
model.add(Input(shape=(lags, 1)))  # Para RNN, GRU, LSTM, input debe ser 3D

for layer in range(n_hidden):
  if layer == n_hidden - 1:
    # Si es la última capa LSTM: return_sequences=False
    model.add(LSTM(units, activation=activation, return_sequences=False))
  else:
    # Si no es la última capa LSTM: return_sequences=True
    model.add(LSTM(units, activation=activation, return_sequences=True))

model.add(Dense(1))

model.compile(optimizer=optimizers.Adam(learning_rate=lr), loss="mse")

history = model.fit(X_train, y_train,
                    validation_data=(X_test, y_test),
                    epochs=epochs,
                    batch_size=batch_size,
                    verbose=0)

# Gráfico de Loss y Val_loss:
plt.figure(figsize=(8,4))
plt.plot(history.history["loss"], label="Loss")
plt.plot(history.history["val_loss"], label="Val_loss")
plt.legend()
plt.show()

# Evaluación del modelo:
y_train_pred = model.predict(X_train, verbose=0)
y_test_pred = model.predict(X_test, verbose=0)

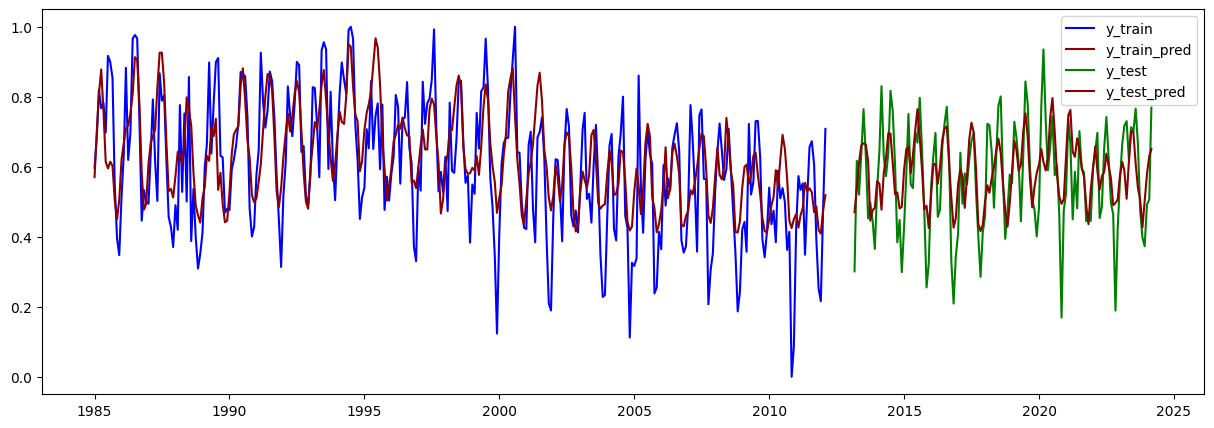
# Graficar y_train y_train_pred:
plt.figure(figsize=(15,5))
plt.plot(train.iloc[lags:].index, y_train, label="y_train", color="blue")
plt.plot(train.iloc[lags:].index, y_train_pred, label="y_train_pred", color="darkred")
plt.plot(test.iloc[lags:].index, y_test, label="y_test", color="green")
plt.plot(test.iloc[lags:].index, y_test_pred, label="y_test_pred", color="darkred")
plt.legend()
plt.show()

# Evaluar el modelo con MSE y R cuadrado:
mse_train = mean_squared_error(y_train, y_train_pred)
mse_test = mean_squared_error(y_test, y_test_pred)
r2_train = r2_score(y_train, y_train_pred)
r2_test = r2_score(y_test, y_test_pred)
print("MSE Train: ", mse_train)
print("MSE Test: ", mse_test)
print("R2 Train: ", r2_train)
print("R2 Test: ", r2_test)

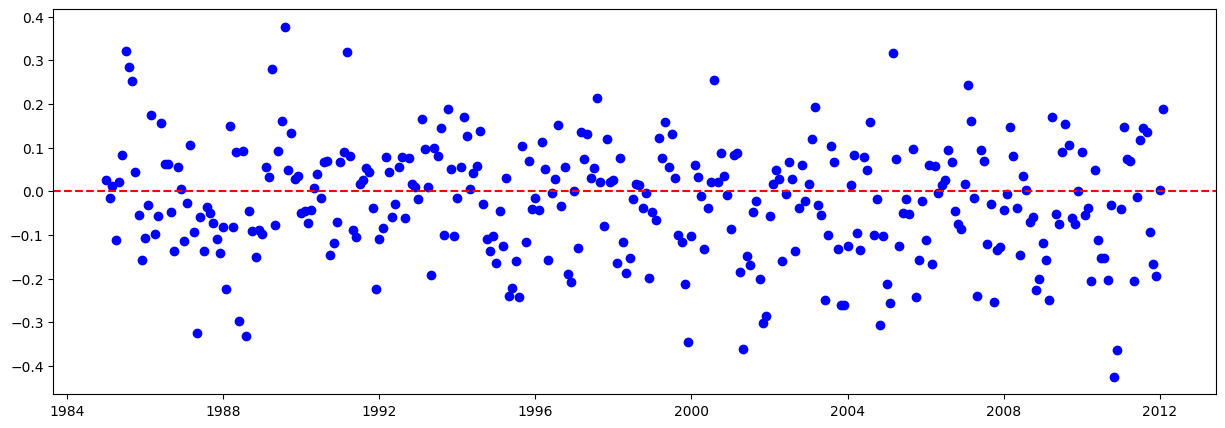
# Graficar los residuales:
residuales = y_train - y_train_pred.flatten()
plt.figure(figsize=(15,5))
plt.scatter(train.iloc[lags:].index, residuales, color="blue")
plt.axhline(y=0, color="red", linestyle="--")
plt.show()
normaltest_result = normaltest(residuales)
shapiro_result = shapiro(residuales)
ks_result = kstest(residuales, "norm")

print("(D'Agostino's K^2):")
if normaltest_result.pvalue < 0.05:
    print("Los residuos NO siguen una distribución normal.")
else:
    print("Los residuos siguen una distribución normal.")
print("")

print("Shapiro-Wilk:")
if shapiro_result.pvalue < 0.05:
    print("Los residuos NO siguen una distribución normal.")
else:
    print("Los residuos siguen una distribución normal.")
print("")

print("Kolmogorov-Smirnov:")
if ks_result.pvalue < 0.05:
    print("Los residuos NO siguen una distribución normal.")
else:
    print("Los residuos siguen una distribución normal.")

../../../_images/output_14_06.png

../../../_images/output_14_13.png

MSE Train:  0.01733649887371953
MSE Test:  0.012221322801097613
R2 Train:  0.5134887543002946
R2 Test:  0.4359748003230959

../../../_images/output_14_3.png

(D'Agostino's K^2):
Los residuos siguen una distribución normal.

Shapiro-Wilk:
Los residuos siguen una distribución normal.

Kolmogorov-Smirnov:
Los residuos NO siguen una distribución normal.

CNN:#

# Red CNN:

# Creación de lags:
lags = 12
X_train, y_train = prepare_data_rnn(train_scaled, lags)
X_test, y_test = prepare_data_rnn(test_scaled, lags)

# Hiperparámetros:
units = 20
n_hidden = 2
activation = "relu"
lr = 0.001
epochs = 50
batch_size = 32

# Hiperparmátros para CNN:
filtros = 32
kernel_size = 3
pool_size = 2
n_hidde_cnn = 2

# Creación de la red:
model = Sequential()
model.add(Input(shape=(lags, 1)))  # Para RNN, GRU, LSTM, input debe ser 3D

for _ in range(n_hidde_cnn):
  model.add(Conv1D(filters=filtros, kernel_size=kernel_size, activation=activation))
  model.add(MaxPooling1D(pool_size=pool_size))

model.add(Flatten())

for _ in range(n_hidden):
  model.add(Dense(units, activation=activation))

model.add(Dense(1))

model.compile(optimizer=optimizers.Adam(learning_rate=lr), loss="mse")

history = model.fit(X_train, y_train,
                    validation_data=(X_test, y_test),
                    epochs=epochs,
                    batch_size=batch_size,
                    verbose=0)

# Gráfico de Loss y Val_loss:
plt.figure(figsize=(8,4))
plt.plot(history.history["loss"], label="Loss")
plt.plot(history.history["val_loss"], label="Val_loss")
plt.legend()
plt.show()

# Evaluación del modelo:
y_train_pred = model.predict(X_train, verbose=0)
y_test_pred = model.predict(X_test, verbose=0)

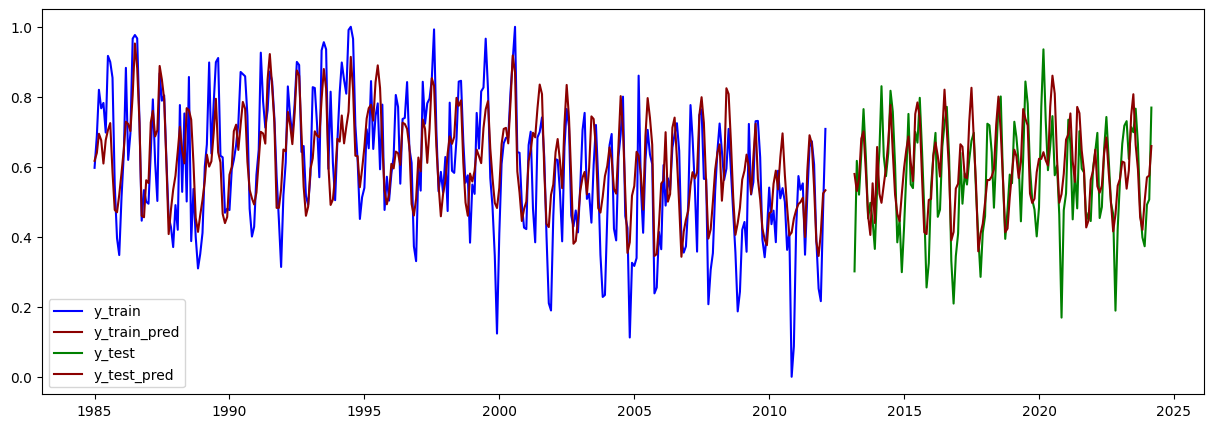
# Graficar y_train y_train_pred:
plt.figure(figsize=(15,5))
plt.plot(train.iloc[lags:].index, y_train, label="y_train", color="blue")
plt.plot(train.iloc[lags:].index, y_train_pred, label="y_train_pred", color="darkred")
plt.plot(test.iloc[lags:].index, y_test, label="y_test", color="green")
plt.plot(test.iloc[lags:].index, y_test_pred, label="y_test_pred", color="darkred")
plt.legend()
plt.show()

# Evaluar el modelo con MSE y R cuadrado:
mse_train = mean_squared_error(y_train, y_train_pred)
mse_test = mean_squared_error(y_test, y_test_pred)
r2_train = r2_score(y_train, y_train_pred)
r2_test = r2_score(y_test, y_test_pred)
print("MSE Train: ", mse_train)
print("MSE Test: ", mse_test)
print("R2 Train: ", r2_train)
print("R2 Test: ", r2_test)

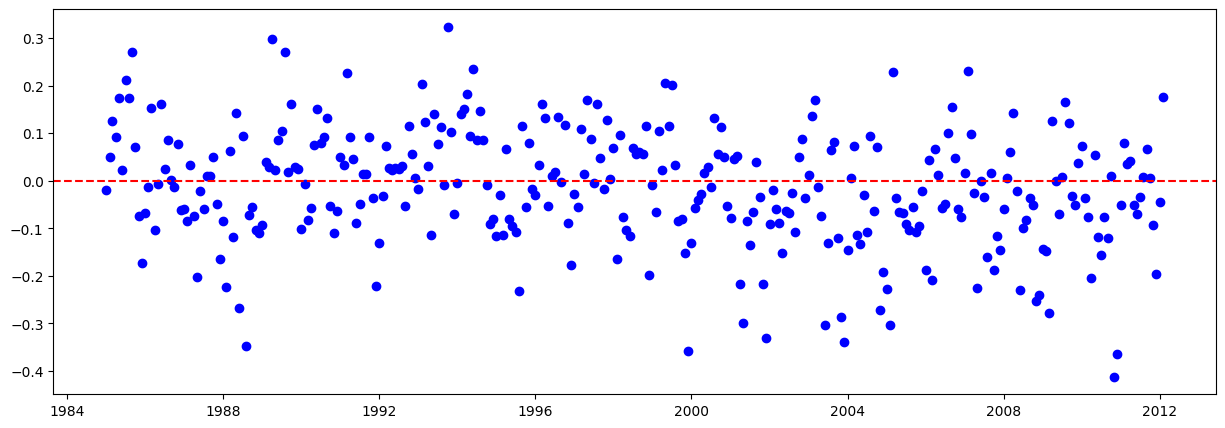
# Graficar los residuales:
residuales = y_train - y_train_pred.flatten()
plt.figure(figsize=(15,5))
plt.scatter(train.iloc[lags:].index, residuales, color="blue")
plt.axhline(y=0, color="red", linestyle="--")
plt.show()
normaltest_result = normaltest(residuales)
shapiro_result = shapiro(residuales)
ks_result = kstest(residuales, "norm")

print("(D'Agostino's K^2):")
if normaltest_result.pvalue < 0.05:
    print("Los residuos NO siguen una distribución normal.")
else:
    print("Los residuos siguen una distribución normal.")
print("")

print("Shapiro-Wilk:")
if shapiro_result.pvalue < 0.05:
    print("Los residuos NO siguen una distribución normal.")
else:
    print("Los residuos siguen una distribución normal.")
print("")

print("Kolmogorov-Smirnov:")
if ks_result.pvalue < 0.05:
    print("Los residuos NO siguen una distribución normal.")
else:
    print("Los residuos siguen una distribución normal.")

../../../_images/output_16_08.png

../../../_images/output_16_12.png

MSE Train:  0.015428864037380254
MSE Test:  0.012785117792577003
R2 Train:  0.5670223891667014
R2 Test:  0.4099551469826702

../../../_images/output_16_3.png

(D'Agostino's K^2):
Los residuos NO siguen una distribución normal.

Shapiro-Wilk:
Los residuos NO siguen una distribución normal.

Kolmogorov-Smirnov:
Los residuos NO siguen una distribución normal.

CNN-LSTM:#

# Función para crear los lags con entradas los valores y la cantidad de lags:
def prepare_data_cnn_lstm(precio, n_lags):
    X = []
    y = []
    for i in range(n_lags, len(precio)):

        lag_features = precio[i - n_lags : i, 0]  # Extraemos el vector de lags
        X.append(lag_features)
        # El target es el valor en la posición actual
        y.append(precio[i, 0])

    # Convertimos las listas a numpy.ndarray
    X = np.array(X)
    y = np.array(y)
    X = X.reshape(X.shape[0], 1, n_lags, 1)

    return X, y

# Creación de lags:
lags = 12
X_train, y_train = prepare_data_cnn_lstm(train_scaled, lags)
X_test, y_test = prepare_data_cnn_lstm(test_scaled, lags)

X_train.shape

(326, 1, 12, 1)

# Híbrido CNN-LSTM:

# Creación de lags:
lags = 24
X_train, y_train = prepare_data_cnn_lstm(train_scaled, lags)
X_test, y_test = prepare_data_cnn_lstm(test_scaled, lags)

# Hiperparámetros:
units = 20
n_hidden = 1
activation = "relu"
lr = 0.001
epochs = 50
batch_size = 32

# Hiperparmátros para CNN:
filtros = 32
kernel_size = 3
pool_size = 2
n_hidde_cnn = 2

# Creación de la red:
model = Sequential()
model.add(Input(shape=(None, lags, 1)))  # Para RNN, GRU, LSTM, input debe ser 3D

for _ in range(n_hidde_cnn):
  model.add(TimeDistributed(Conv1D(filters=filtros, kernel_size=kernel_size, activation=activation)))
  model.add(TimeDistributed(MaxPooling1D(pool_size=pool_size)))

model.add(TimeDistributed(Flatten()))

for layer in range(n_hidden):
  if layer == n_hidden - 1:
    # Si es la última capa LSTM: return_sequences=False
    model.add(LSTM(units, activation=activation, return_sequences=False))
  else:
    # Si no es la última capa LSTM: return_sequences=True
    model.add(LSTM(units, activation=activation, return_sequences=True))

model.add(Dense(1))

model.compile(optimizer=optimizers.Adam(learning_rate=lr), loss="mse")

history = model.fit(X_train, y_train,
                    validation_data=(X_test, y_test),
                    epochs=epochs,
                    batch_size=batch_size,
                    verbose=0)

# Gráfico de Loss y Val_loss:
plt.figure(figsize=(8,4))
plt.plot(history.history["loss"], label="Loss")
plt.plot(history.history["val_loss"], label="Val_loss")
plt.legend()
plt.show()

# Evaluación del modelo:
y_train_pred = model.predict(X_train, verbose=0).flatten() ###### agregar flatten() ######
y_test_pred = model.predict(X_test, verbose=0).flatten() ###### agregar flatten() ######

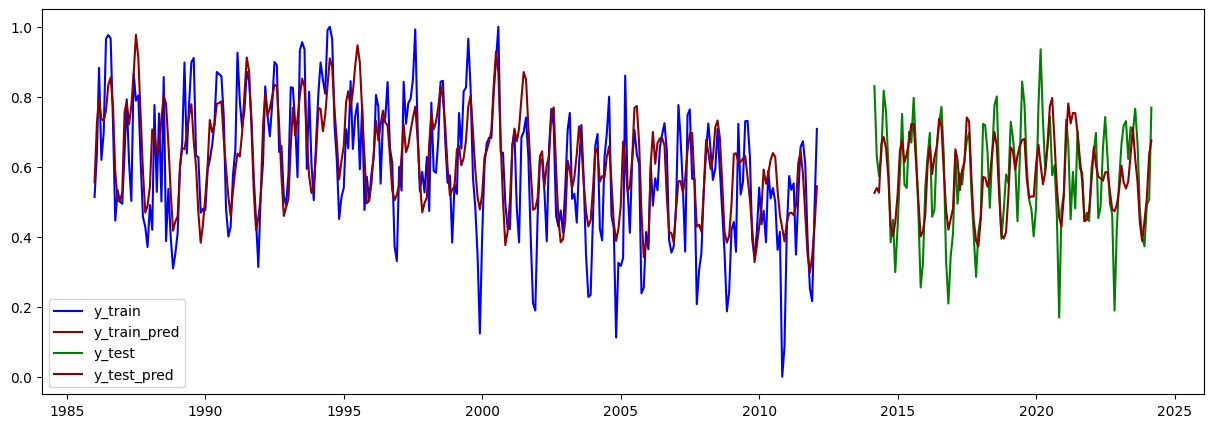
# Graficar y_train y_train_pred:
plt.figure(figsize=(15,5))
plt.plot(train.iloc[lags:].index, y_train, label="y_train", color="blue")
plt.plot(train.iloc[lags:].index, y_train_pred, label="y_train_pred", color="darkred")
plt.plot(test.iloc[lags:].index, y_test, label="y_test", color="green")
plt.plot(test.iloc[lags:].index, y_test_pred, label="y_test_pred", color="darkred")
plt.legend()
plt.show()

# Evaluar el modelo con MSE y R cuadrado:
mse_train = mean_squared_error(y_train, y_train_pred)
mse_test = mean_squared_error(y_test, y_test_pred)
r2_train = r2_score(y_train, y_train_pred)
r2_test = r2_score(y_test, y_test_pred)
print("MSE Train: ", mse_train)
print("MSE Test: ", mse_test)
print("R2 Train: ", r2_train)
print("R2 Test: ", r2_test)

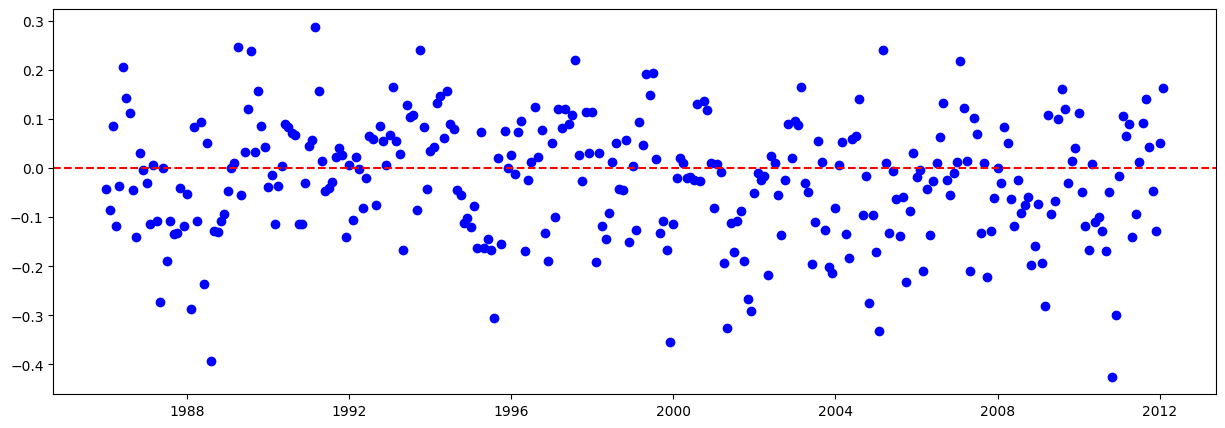
# Graficar los residuales:
residuales = y_train - y_train_pred.flatten()
plt.figure(figsize=(15,5))
plt.scatter(train.iloc[lags:].index, residuales, color="blue")
plt.axhline(y=0, color="red", linestyle="--")
plt.show()
normaltest_result = normaltest(residuales)
shapiro_result = shapiro(residuales)
ks_result = kstest(residuales, "norm")

print("(D'Agostino's K^2):")
if normaltest_result.pvalue < 0.05:
    print("Los residuos NO siguen una distribución normal.")
else:
    print("Los residuos siguen una distribución normal.")
print("")

print("Shapiro-Wilk:")
if shapiro_result.pvalue < 0.05:
    print("Los residuos NO siguen una distribución normal.")
else:
    print("Los residuos siguen una distribución normal.")
print("")

print("Kolmogorov-Smirnov:")
if ks_result.pvalue < 0.05:
    print("Los residuos NO siguen una distribución normal.")
else:
    print("Los residuos siguen una distribución normal.")

../../../_images/output_20_04.png

../../../_images/output_20_13.png

MSE Train:  0.015089972659474777
MSE Test:  0.01183731215465527
R2 Train:  0.5740489209708091
R2 Test:  0.46424541020426646

../../../_images/output_20_31.png

(D'Agostino's K^2):
Los residuos NO siguen una distribución normal.

Shapiro-Wilk:
Los residuos siguen una distribución normal.

Kolmogorov-Smirnov:
Los residuos NO siguen una distribución normal.