Solución suavizamiento extracción petróleo

Contents

Solución suavizamiento extracción petróleo#

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt

# Cargar el archivo xlsx:
df = pd.read_excel('Extracción petróleo Ecopetrol.xlsx')

# Corregir nombres de columnas si tienen espacios
df.columns = df.columns.str.strip()

# Convertir 'Fecha' a datetime y usar como índice
df['Fecha'] = pd.to_datetime(df['Fecha'])
df.set_index('Fecha', inplace=True)

# Ordenar por fecha por si acaso
df = df.sort_index()

# Establecer frecuencia explícita para evitar el warning de statsmodels
df.index.freq = df.index.inferred_freq

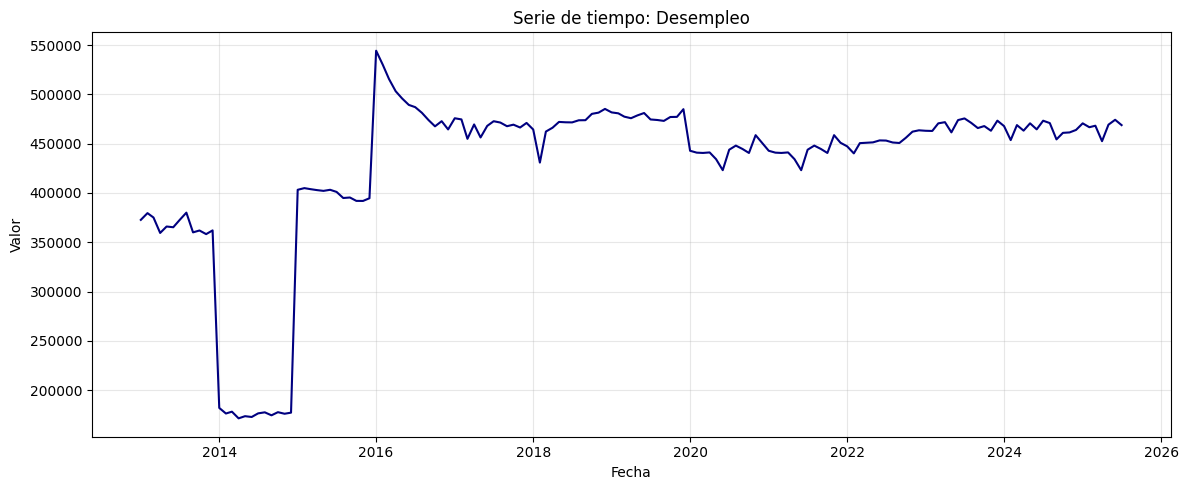
plt.figure(figsize=(12, 5))
plt.plot(df, color='navy')
plt.title("Serie de tiempo: Desempleo")
plt.xlabel("Fecha")
plt.ylabel("Valor")
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()

df.head()

../../_images/output_2_06.png

	Serie
Fecha
2013-01-01	372721.422903
2013-02-01	379569.167143
2013-03-01	375120.390968
2013-04-01	359475.416667
2013-05-01	366006.581935

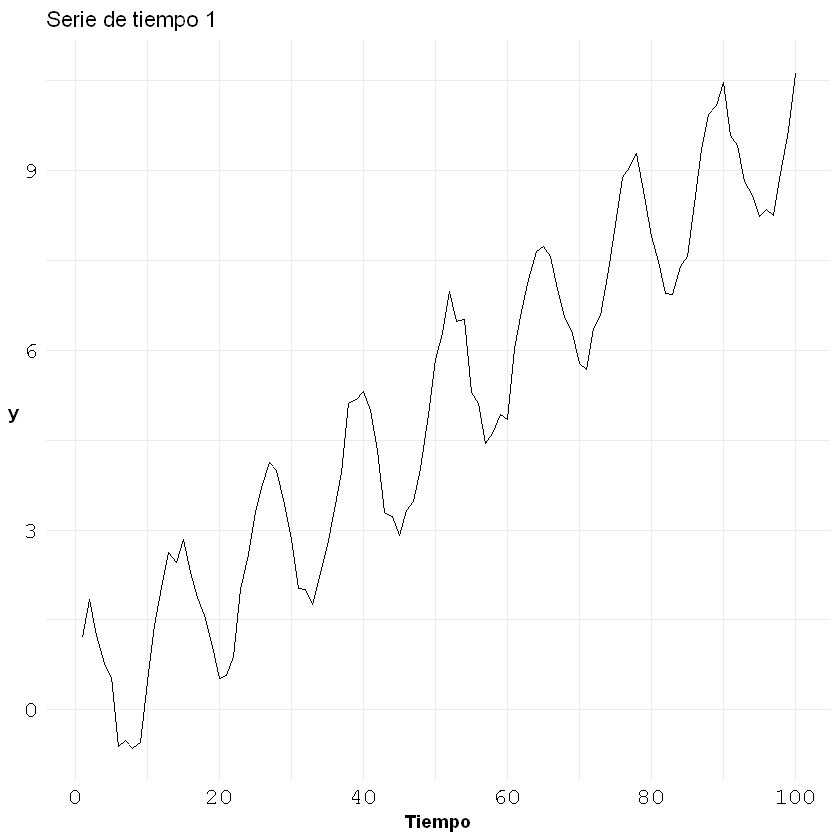
Serie de tiempo:#

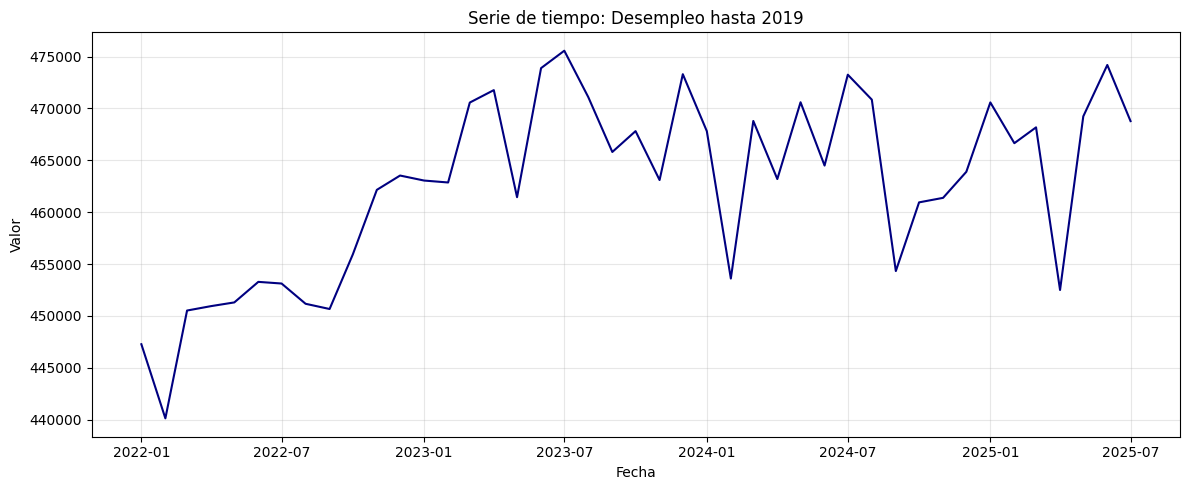
serie = df.loc['2022-01-01':]

plt.figure(figsize=(12, 5))
plt.plot(serie, color='navy')
plt.title("Serie de tiempo: Desempleo hasta 2019")
plt.xlabel("Fecha")
plt.ylabel("Valor")
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()

from statsmodels.tsa.seasonal import seasonal_decompose

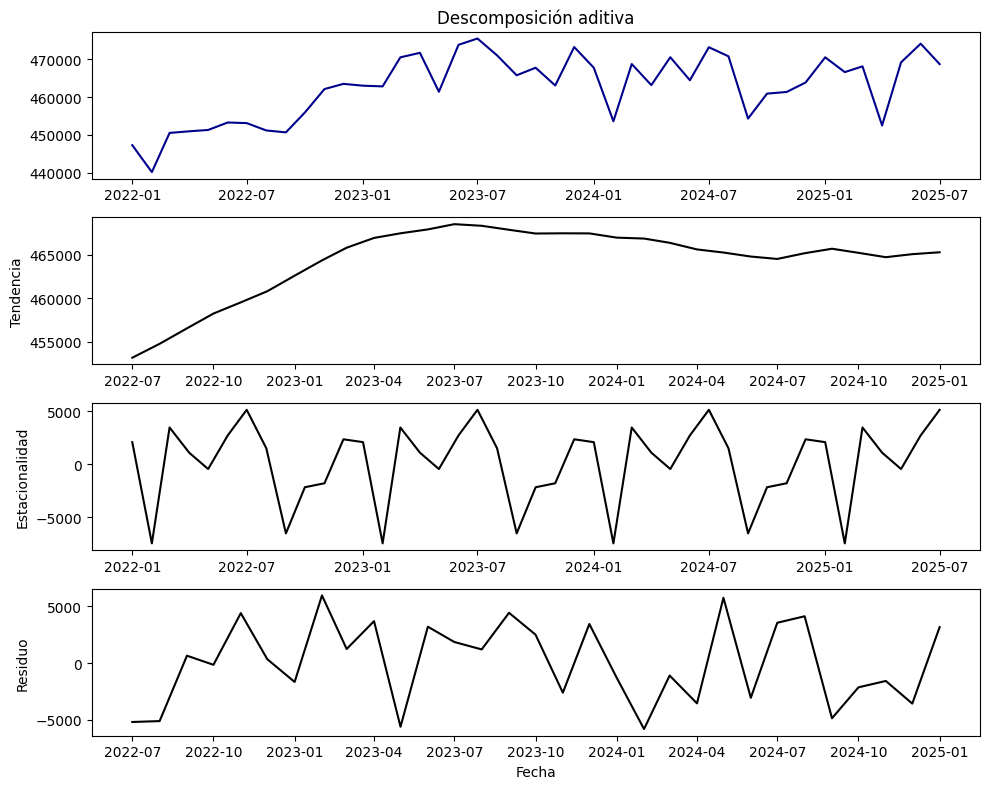
# Descomposición aditiva (periodo de 12 meses)
result_add = seasonal_decompose(serie, model="additive", period=12)

# Graficar
plt.figure(figsize=(10, 8))
plt.subplot(4, 1, 1)
plt.plot(result_add.observed, color="darkblue")
plt.title("Descomposición aditiva")

plt.subplot(4, 1, 2)
plt.plot(result_add.trend, color="black")
plt.ylabel("Tendencia")

plt.subplot(4, 1, 3)
plt.plot(result_add.seasonal, color="black")
plt.ylabel("Estacionalidad")

plt.subplot(4, 1, 4)
plt.plot(result_add.resid, color="black")
plt.ylabel("Residuo")
plt.xlabel("Fecha")

plt.tight_layout()
plt.show()

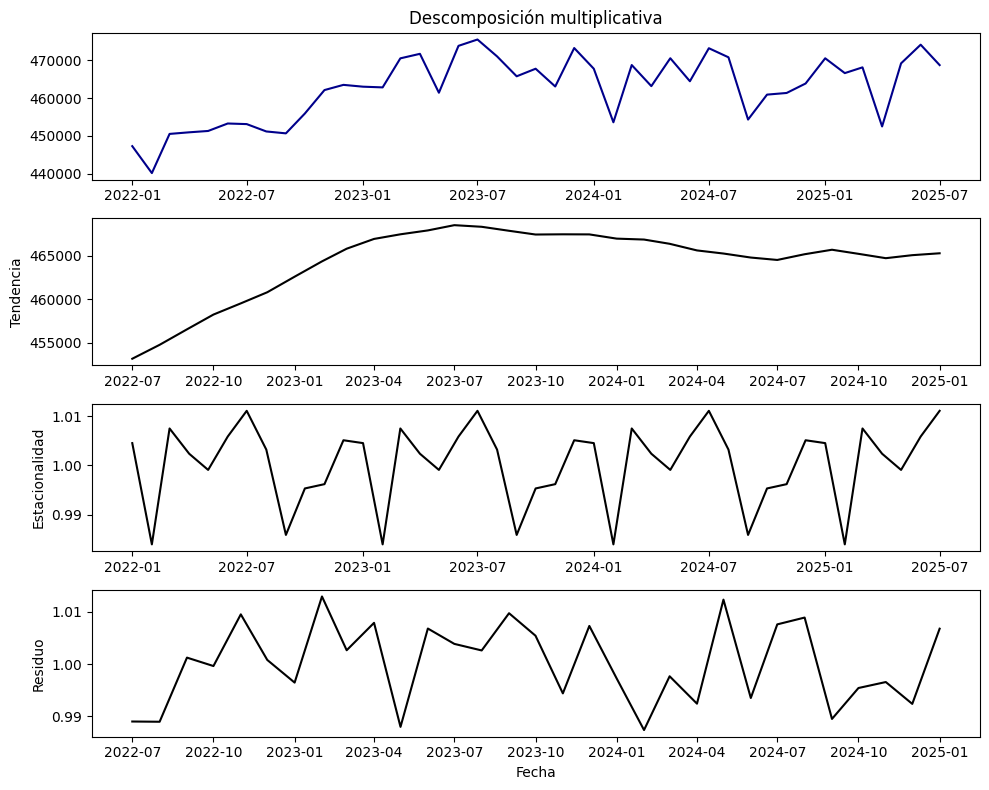
# Descomposición multiplicativa (periodo de 12 meses)
result_add = seasonal_decompose(serie, model="multiplicative", period=12)

# Graficar
plt.figure(figsize=(10, 8))
plt.subplot(4, 1, 1)
plt.plot(result_add.observed, color="darkblue")
plt.title("Descomposición multiplicativa")

plt.subplot(4, 1, 2)
plt.plot(result_add.trend, color="black")
plt.ylabel("Tendencia")

plt.subplot(4, 1, 3)
plt.plot(result_add.seasonal, color="black")
plt.ylabel("Estacionalidad")

plt.subplot(4, 1, 4)
plt.plot(result_add.resid, color="black")
plt.ylabel("Residuo")
plt.xlabel("Fecha")

plt.tight_layout()
plt.show()

../../_images/output_4_011.png

../../_images/output_4_1.png

../../_images/output_4_21.png

Conjunto de train y test:#

# Dividir en train y test (por ejemplo, 80% train, 20% test)
split = int(len(serie) * 0.8)
train, test = serie[:split], serie[split:]

# Graficar train y test:

plt.figure(figsize=(12, 5))
plt.plot(train, label='Train', color='navy')
plt.plot(test, label='Test', color='orange')
plt.title("Conjunto de train y test")
plt.xlabel("Fecha")
plt.ylabel("Valor")
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()

../../_images/output_6_0.png

Ajuste métodos de suavizamiento:#

from statsmodels.tsa.holtwinters import SimpleExpSmoothing, Holt, ExponentialSmoothing
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error, max_error, explained_variance_score

# Ajustar modelos de suavizamiento
# a) Simple Exponential Smoothing
model_ses = SimpleExpSmoothing(train).fit(optimized=True)
y_train_pred_ses = model_ses.fittedvalues
y_pred_test_ses = model_ses.forecast(len(test))

# b) Holt (Doble suavizamiento)
model_holt = Holt(train).fit(optimized=True)
y_train_pred_holt = model_holt.fittedvalues
y_pred_test_holt = model_holt.forecast(len(test))

# c) Holt-Winters (Triple suavizamiento, aditivo, estacionalidad anual si mensual)
estacionalidad = 12 if train.index.freqstr in ['M', 'MS'] else None
model_hw = ExponentialSmoothing(train, trend='add', seasonal='add', seasonal_periods=estacionalidad).fit(optimized=True)
y_train_pred_hw = model_hw.fittedvalues
y_pred_test_hw = model_hw.forecast(len(test))

# Graficar los ajustes y predicciones
plt.figure(figsize=(12, 5))
plt.plot(serie, label='Serie original', color='black')
plt.plot(y_train_pred_ses, label=f'SES - Ajuste: alfa {model_ses.params['smoothing_level']:.2f}', color='dodgerblue')
plt.plot(y_train_pred_holt, label=f'Holt - Ajuste: alfa {model_holt.params['smoothing_level']:.2f}, Beta {model_holt.params['smoothing_trend']:.2f}', color='green')
plt.plot(y_train_pred_holt, label=f'HW - Ajuste: alfa {model_hw.params['smoothing_level']:.2f}, Beta {model_hw.params['smoothing_trend']:.2f}, gamma {model_hw.params['smoothing_seasonal']:.2f}', color='orange')
plt.plot(test.index, y_pred_test_ses, label='SES - Pronóstico', ls='--', color='blue')
plt.plot(test.index, y_pred_test_holt, label='Holt - Pronóstico', ls='--', color='green')
plt.plot(test.index, y_pred_test_hw, label='HW - Pronóstico', ls='--', color='orange')
plt.legend()
plt.title('Ajuste y Pronóstico con Métodos de Suavizamiento')
plt.show()


### Métricas de desempeño:

from sklearn.metrics import (
    r2_score, mean_absolute_error, mean_squared_error,
    max_error, mean_absolute_percentage_error, explained_variance_score
)

# Función para calcular todas las métricas
def calcular_metricas(y_true, y_pred):
    metrics = {}
    metrics['R2'] = r2_score(y_true, y_pred)
    metrics['MAE'] = mean_absolute_error(y_true, y_pred)
    metrics['MSE'] = mean_squared_error(y_true, y_pred)
    metrics['RMSE'] = np.sqrt(metrics['MSE'])
    # Evitar división por cero en MAPE:
    metrics['MAPE'] = mean_absolute_percentage_error(y_true, y_pred) if np.max(np.abs(y_true)) > 0 else 0
    metrics['Max Error'] = max_error(y_true, y_pred)
    metrics['Explained Variance'] = explained_variance_score(y_true, y_pred)
    return metrics

# Calcular métricas en train para cada modelo
metrics_ses_train = calcular_metricas(train, y_train_pred_ses)
metrics_holt_train = calcular_metricas(train, y_train_pred_holt)
metrics_hw_train = calcular_metricas(train, y_train_pred_hw)

# Calcular métricas en Test para cada modelo
metrics_ses = calcular_metricas(test, y_pred_test_ses)
metrics_holt = calcular_metricas(test, y_pred_test_holt)
metrics_hw = calcular_metricas(test, y_pred_test_hw)

# Mostrar resultados en tabla para train:
resultados_train = pd.DataFrame({
    "SES": metrics_ses_train,
    "Holt": metrics_holt_train,
    "Holt-Winters": metrics_hw_train
})
print("Métricas de desempeño en el conjunto de train:")
display(resultados_train)

# Mostrar resultados en tabla para test:
resultados = pd.DataFrame({
    "SES": metrics_ses,
    "Holt": metrics_holt,
    "Holt-Winters": metrics_hw
})
print("\nMétricas de desempeño en el conjunto de test:")
display(resultados)

../../_images/output_9_011.png

Métricas de desempeño en el conjunto de train:

	SES	Holt	Holt-Winters
R2	5.279205e-01	3.309102e-01	6.151194e-01
MAE	4.978838e+03	5.656661e+03	4.577064e+03
MSE	3.824801e+07	5.420984e+07	3.118313e+07
RMSE	6.184498e+03	7.362733e+03	5.584186e+03
MAPE	1.077755e-02	1.228558e-02	9.929617e-03
Max Error	1.560650e+04	1.863465e+04	1.184765e+04
Explained Variance	5.396558e-01	3.366695e-01	6.158941e-01

Métricas de desempeño en el conjunto de test:

	SES	Holt	Holt-Winters
R2	-4.717982e-01	-9.386793e+00	-4.323733e-01
MAE	6.369051e+03	1.664740e+04	5.711667e+03
MSE	5.222924e+07	3.685929e+08	5.083018e+07
RMSE	7.226980e+03	1.919877e+04	7.129529e+03
MAPE	1.363985e-02	3.550286e-02	1.234258e-02
Max Error	1.212926e+04	3.146440e+04	1.660011e+04
Explained Variance	-2.220446e-16	-1.577220e+00	-3.748616e-01

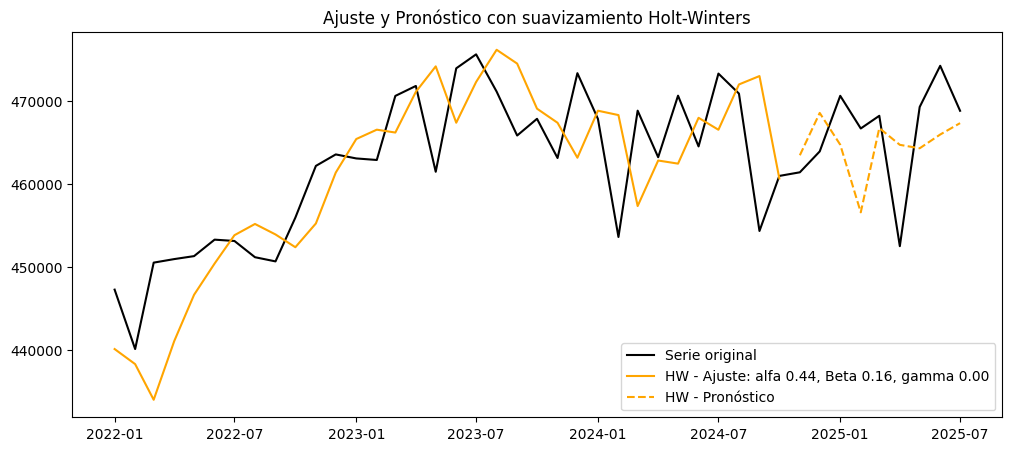
Ajuste con parámetros específicos:#

# c) Holt-Winters:
model_hw = ExponentialSmoothing(train, trend='multiplicative', seasonal='add',
                                seasonal_periods=estacionalidad).fit(smoothing_level=0.3,
                                                                     smoothing_trend=0.01,
                                                                     smoothing_seasonal=0.5)

model_hw = ExponentialSmoothing(train, trend='multiplicative', seasonal='add',
                                seasonal_periods=estacionalidad).fit(optimized=True)
y_train_pred_hw = model_hw.fittedvalues
y_pred_test_hw = model_hw.forecast(len(test))

# Graficar los ajustes y predicciones
plt.figure(figsize=(12, 5))
plt.plot(serie, label='Serie original', color='black')
plt.plot(y_train_pred_holt, label=f'HW - Ajuste: alfa {model_hw.params['smoothing_level']:.2f}, Beta {model_hw.params['smoothing_trend']:.2f}, gamma {model_hw.params['smoothing_seasonal']:.2f}', color='orange')
plt.plot(test.index, y_pred_test_hw, label='HW - Pronóstico', ls='--', color='orange')
plt.legend()
plt.title('Ajuste y Pronóstico con suavizamiento Holt-Winters')
plt.show()


### Métricas de desempeño:
# Función para calcular todas las métricas
def calcular_metricas(y_true, y_pred):
    metrics = {}
    metrics['R2'] = r2_score(y_true, y_pred)
    metrics['MAE'] = mean_absolute_error(y_true, y_pred)
    metrics['MSE'] = mean_squared_error(y_true, y_pred)
    metrics['RMSE'] = np.sqrt(metrics['MSE'])
    # Evitar división por cero en MAPE:
    metrics['MAPE'] = mean_absolute_percentage_error(y_true, y_pred) if np.max(np.abs(y_true)) > 0 else 0
    metrics['Max Error'] = max_error(y_true, y_pred)
    metrics['Explained Variance'] = explained_variance_score(y_true, y_pred)
    return metrics

# Calcular métricas en train para el modelo hw:
metrics_hw_train = calcular_metricas(train, y_train_pred_hw)

# Calcular métricas en Test para el modelo hw:
metrics_ses = calcular_metricas(test, y_pred_test_ses)
metrics_holt = calcular_metricas(test, y_pred_test_holt)
metrics_hw = calcular_metricas(test, y_pred_test_hw)

# Mostrar resultados en tabla para train:
resultados_train = pd.DataFrame({
    "Holt-Winters": metrics_hw_train
})
print("Métricas de desempeño en el conjunto de train:")
display(resultados_train)

# Mostrar resultados en tabla para test:
resultados = pd.DataFrame({
    "Holt-Winters": metrics_hw
})
print("\nMétricas de desempeño en el conjunto de test:")
display(resultados)

../../_images/output_11_015.png

Métricas de desempeño en el conjunto de train:

	Holt-Winters
R2	7.693755e-01
MAE	3.131313e+03
MSE	1.868526e+07
RMSE	4.322645e+03
MAPE	6.776449e-03
Max Error	1.184387e+04
Explained Variance	7.741966e-01

Métricas de desempeño en el conjunto de test:

	Holt-Winters
R2	-2.772446e-01
MAE	5.670354e+03
MSE	4.532518e+07
RMSE	6.732398e+03
MAPE	1.220182e-02
Max Error	1.218705e+04
Explained Variance	-2.157130e-01