Exploración visual de series de tiempo#

En esta sección se presenta la exploración y visualización de series de tiempo, un paso fundamental antes de aplicar cualquier técnica de modelado o pronóstico. La observación gráfica permite identificar patrones como la tendencia (cambios persistentes a largo plazo), la estacionalidad (variaciones regulares en periodos específicos), y la presencia de ruido aleatorio o fluctuaciones no sistemáticas. A través de gráficos de línea, histogramas y técnicas de descomposición, podremos desglosar la serie en sus componentes y comprender mejor su estructura, lo que facilitará la selección de modelos adecuados y la interpretación de los resultados en el contexto del problema de estudio.

Exploración y visualización de la TRM en Colombia:#

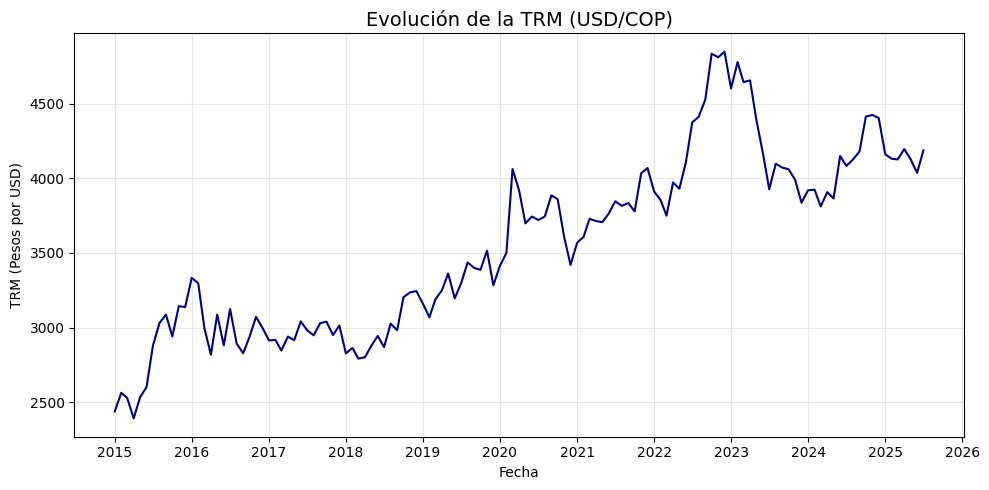
En este ejercicio descargaremos y visualizaremos la Tasa Representativa del Mercado (TRM) de Colombia, expresada como la cantidad de pesos colombianos por un dólar estadounidense (USD/COP). Para ello, utilizaremos datos históricos desde enero de 2015 hasta julio de 2025, con frecuencia mensual, extraídos desde Yahoo Finance.

Descarga de datos desde Yahoo Finance:

Usaremos la librería yfinance para acceder a la TRM histórica. En Yahoo Finance, el ticker correspondiente a la TRM es USDCOP=X.

import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.dates as mdates

# Descargar datos mensuales desde 2015
start_date = "2015-01-01"
end_date = "2025-07-31"

# TRM de Colombia (USD/COP)
trm = yf.download("USDCOP=X", start=start_date, end=end_date, interval='1mo', auto_adjust=False)['Close']
trm.name = 'TRM (USD/COP)'

[*******************100%*********************]  1 of 1 completed

interval='1mo' indica que queremos datos con frecuencia mensual.
El campo 'Close' se refiere al precio de cierre para cada periodo.
Se asigna un nombre descriptivo a la serie: "TRM (USD/COP)".

Visualización de la serie de tiempo:

Para analizar la evolución de la TRM, graficaremos la serie usando matplotlib. Configuraremos el formato de fechas para que los ejes sean claros.

# Crear figura
plt.figure(figsize=(10, 5))
plt.plot(trm.index, trm, linestyle='-', color='navy')

# Personalización del gráfico
plt.title("Evolución de la TRM (USD/COP)", fontsize=14)
plt.xlabel("Fecha")
plt.ylabel("TRM (Pesos por USD)")
plt.grid(True, alpha=0.3)

# Formato de fechas en el eje X
plt.gca().xaxis.set_major_locator(mdates.YearLocator())
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter('%Y'))

plt.tight_layout()
plt.show()

Estadísticas descriptivas:

estadisticas_trm = trm.describe()

print("Estadísticas descriptivas de la TRM (USD/COP):\n")
print(estadisticas_trm)

Estadísticas descriptivas de la TRM (USD/COP):

Ticker     USDCOP=X
count    127.000000
mean    3551.674253
std      598.364384
min     2393.000000
25%     3020.584961
50%     3567.260010
75%     4034.344971
max     4846.919922

Histograma de la TRM:

El histograma nos permite visualizar la distribución de los valores de la TRM a lo largo del tiempo, identificando si se concentra en ciertos rangos o si presenta colas largas (valores extremos).

plt.figure(figsize=(8, 5))
plt.hist(trm, bins=20, color='skyblue', edgecolor='black')
plt.title("Distribución histórica de la TRM (USD/COP)", fontsize=14)
plt.xlabel("TRM (Pesos por USD)")
plt.ylabel("Frecuencia")
plt.grid(axis='y', alpha=0.3)
plt.tight_layout()
plt.show()

Un histograma muy disperso sugiere alta volatilidad.
Picos y colas pueden asociarse a eventos económicos relevantes.

Descomposición aditiva:#

from statsmodels.tsa.seasonal import seasonal_decompose

# Descomposición aditiva (periodo de 12 meses)
result_add = seasonal_decompose(trm, model="additive", period=12)

# Graficar
result_add.plot()
plt.suptitle("Descomposición aditiva - TRM", fontsize=14, y=1.02)
plt.tight_layout()
plt.show()

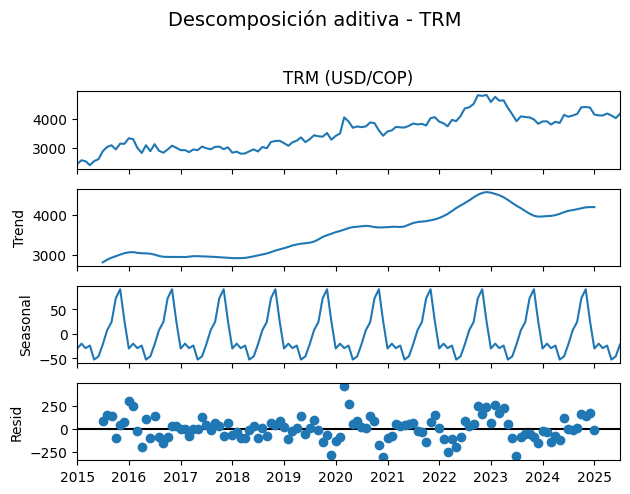
Otra forma de graficar:

# Graficar
plt.figure(figsize=(10, 8))
plt.subplot(4, 1, 1)
plt.plot(result_add.observed, color="darkblue")
plt.title("Descomposición aditiva - TRM")

plt.subplot(4, 1, 2)
plt.plot(result_add.trend, color="black")
plt.ylabel("Tendencia")

plt.subplot(4, 1, 3)
plt.plot(result_add.seasonal, color="black")
plt.ylabel("Estacionalidad")

plt.subplot(4, 1, 4)
plt.plot(result_add.resid, color="black")
plt.ylabel("Residuo")
plt.xlabel("Fecha")

plt.tight_layout()
plt.show()

# Descomposición multiplicativa
result_mul = seasonal_decompose(trm, model="multiplicative", period=12)

# Graficar
plt.figure(figsize=(10, 8))
plt.subplot(4, 1, 1)
plt.plot(result_mul.observed, color="darkblue")
plt.title("Descomposición multiplicativa - TRM")

plt.subplot(4, 1, 2)
plt.plot(result_mul.trend, color="black")
plt.ylabel("Tendencia")

plt.subplot(4, 1, 3)
plt.plot(result_mul.seasonal, color="black")
plt.ylabel("Estacionalidad")

plt.subplot(4, 1, 4)
plt.plot(result_mul.resid, color="black")
plt.ylabel("Residuo")
plt.xlabel("Fecha")

plt.tight_layout()
plt.show()

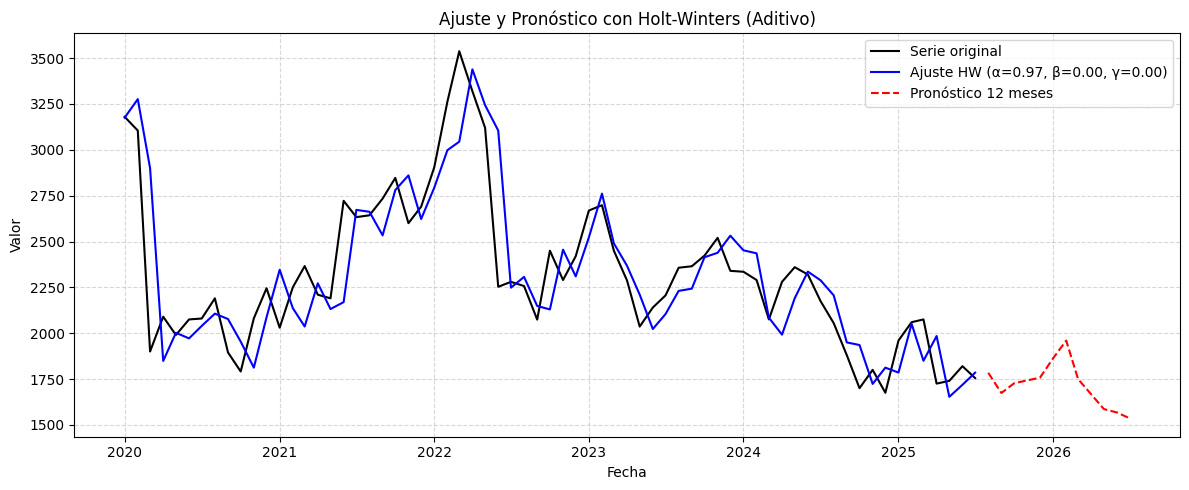
En este caso, la TRM presenta visualmente un comportamiento más acorde con un modelo aditivo, ya que la amplitud de la estacionalidad es prácticamente constante a lo largo del tiempo y no se incrementa con el nivel de la serie. Sin embargo, al aplicar ambos métodos (aditivo y multiplicativo), si la serie fuera verdaderamente multiplicativa, la estacionalidad resultante mostraría variaciones proporcionales al nivel de la tendencia, es decir, ciclos más amplios cuando el valor de la TRM es alto y más pequeños cuando es bajo. Al comparar los residuales de ambas descomposiciones, se observan patrones temporales muy similares —lo que indica que ambos métodos están captando la misma dinámica subyacente—, pero con diferencias en la escala: en el modelo aditivo los residuales están en valores absolutos (pesos COP), mientras que en el multiplicativo se expresan como proporciones respecto al nivel de la serie. Esta diferencia de escala se debe a que el residuo aditivo se obtiene por resta y el multiplicativo por división, lo que cambia la forma en que se amplifican o atenúan las variaciones según el nivel de la serie.

En el modelo aditivo, el residuo es simplemente la resta: \(R_t = Y_t - T_t - S_t\)

En el multiplicativo, es la división: \(R_t = \dfrac{Y_t}{T_t \times S_t}\) Esto hace que las variaciones aleatorias se escalen diferente y que los valores extremos (outliers) tengan distinto peso.

# Comparar residuales en un solo gráfico
plt.figure(figsize=(10, 5))
plt.plot(result_add.resid, label="Residuo - Aditivo", color="black")
plt.plot(result_mul.resid, label="Residuo - Multiplicativo", color="orange", alpha=0.7)
plt.axhline(0, color="gray", linestyle="--", linewidth=1)
plt.title("Comparación de residuales: Aditivo vs Multiplicativo - TRM")
plt.xlabel("Fecha")
plt.ylabel("Valor residual")
plt.legend()
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()

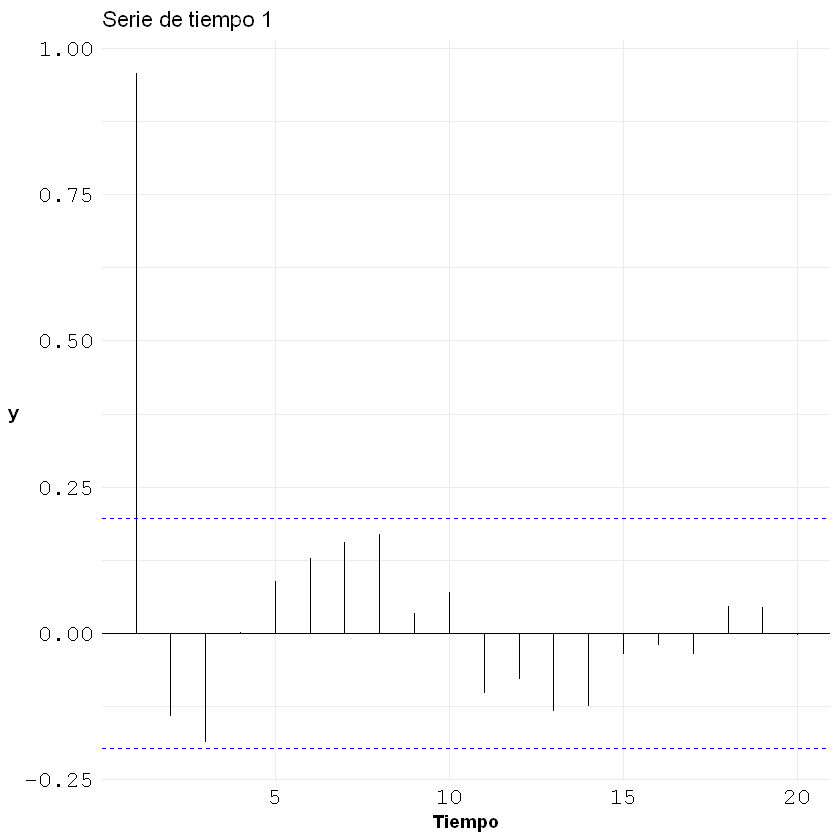
Estimación de la tendencia:#

La tendencia \(( T_t )\) en una serie de tiempo representa su comportamiento de largo plazo, eliminando fluctuaciones de corto plazo y componentes estacionales.

Una forma común de estimarla es mediante un promedio móvil centrado de orden \(m\), que suaviza los valores de la serie a lo largo del tiempo.

La fórmula general para calcular la tendencia mediante un promedio móvil centrado es:

\[T_t = \frac{1}{m} \sum_{i = -k}^{k} Y_{t+i}\]

donde:

\(Y_t\) es el valor observado de la serie en el tiempo \(t\),
\(m\) es el número de periodos en la ventana del promedio (por ejemplo, \(m = 12\) para datos mensuales con estacionalidad anual),
\(k = \frac{m}{2}\) si \(m\) es par (en cuyo caso se ajusta usando medias móviles dobles),
\(k = \frac{m-1}{2}\) si \(m\) es impar.

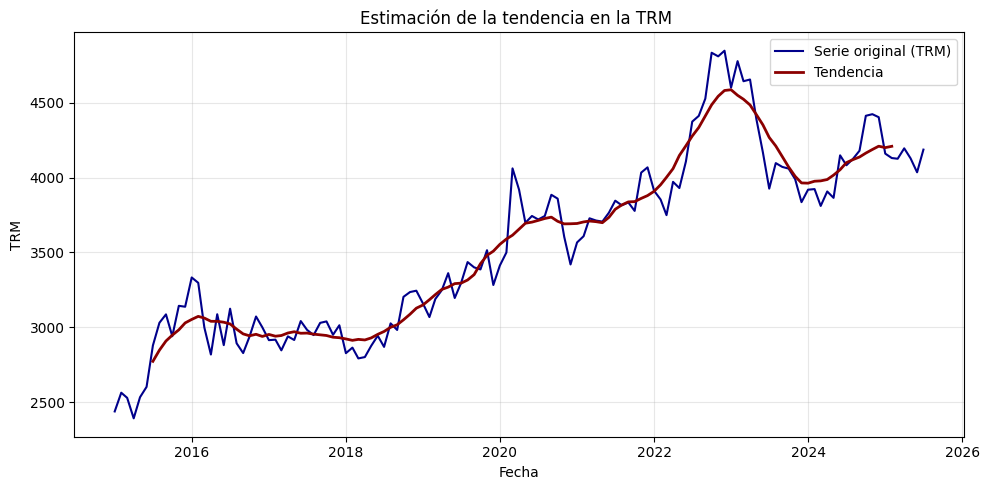
Este promedio suaviza los datos al considerar los valores anteriores y posteriores a cada punto de tiempo \(t\), y permite observar la dirección general de la serie, facilitando el análisis de su comportamiento estructural.

# Calcular la tendencia con un promedio móvil centrado de 12 meses
tendencia = trm.rolling(window=12, center=True).mean()

# Graficar la serie original y la tendencia
plt.figure(figsize=(10, 5))
plt.plot(trm, label="Serie original (TRM)", color="darkblue")
plt.plot(tendencia, label="Tendencia", color="darkred", linewidth=2)
plt.title("Estimación de la tendencia en la TRM ")
plt.xlabel("Fecha")
plt.ylabel("TRM")
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()

Estimación de la estacionalidad aditiva:#

La estacionalidad \((S_t)\) representa fluctuaciones que se repiten con una periodicidad fija, como los efectos mensuales, trimestrales o anuales.

Una vez se ha estimado la tendencia \(T_t\), la serie se “deseasonaliza” de forma aditiva mediante:

\[Y_t - T_t = S_t + R_t\]

Luego, para estimar \(S_t\), se agrupan los valores por posición dentro del ciclo (por ejemplo, por mes calendario) y se calcula el promedio para cada mes:

\[S_j = \frac{1}{n_j} \sum_{t \in \text{mes } j} (Y_t - T_t)\]

donde:

\(S_j\): índice estacional del mes \(j\) (por ejemplo, enero, febrero, etc.),
\(n_j\): número de años disponibles para el mes \(j\).

Finalmente, se centra la estacionalidad para asegurar que su efecto promedio sea nulo:

\[\sum_{j=1}^{m} S_j = 0\]

Esto garantiza que la estacionalidad no modifique el nivel general de la serie.

# 1. Calcular la tendencia con media móvil centrada de 12 meses
tendencia = trm.rolling(window=12, center=True).mean()

# 2. Calcular la serie sin tendencia
detrended = trm - tendencia

# 3. Calcular el promedio mensual de la serie sin tendencia
# Agrupar por mes calendario (1=enero, ..., 12=diciembre)
promedio_mensual = detrended.groupby(detrended.index.month).mean()

# 4. Centrar los valores mensuales (que sumen cero)
estacionalidad = promedio_mensual - promedio_mensual.mean()
estacionalidad.index.name = "Mes"
estacionalidad.name = "Índice estacional aditivo"

plt.figure(figsize=(4, 4))
plt.plot(estacionalidad.index, estacionalidad.values, marker='o', linestyle='-', color='black')
plt.axhline(0, color='gray', linestyle='--')
plt.title("Estacionalidad aditiva mensual estimada")
plt.xlabel("Mes (1 = Enero, ..., 12 = Diciembre)")
plt.ylabel("Índice estacional aditivo")
plt.xticks(ticks=range(1, 13))
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()

Estimación del residuo:#

Una vez estimados los \(S_t\), se puede calcular el residuo aditivo como:

\[R_t = Y_t - T_t - S_t\]

# Paso clave: asegurarse de que 'estacionalidad' es una Serie válida con índice de 1 a 12
estacionalidad = estacionalidad.astype(float)
estacionalidad.index = estacionalidad.index.astype(int)

# Expandir estacionalidad según el mes de cada fecha en trm
estacionalidad_expandida = trm.index.to_series().apply(lambda fecha: estacionalidad.loc[fecha.month])
estacionalidad_expandida.index = trm.index  # asegurar índice alineado

# Calcular el residuo
residuo = trm - tendencia - estacionalidad_expandida
residuo = residuo.dropna()  # eliminar NaN por los bordes de la media móvil

# Graficar el residuo
plt.figure(figsize=(10, 5))
plt.plot(residuo, color='teal', label='Residuo aditivo')
plt.axhline(0, color='gray', linestyle='--')
plt.title("Residuo aditivo: $R_t = Y_t - T_t - S_t$")
plt.xlabel("Fecha")
plt.ylabel("Residuo")
plt.grid(True, alpha=0.3)
plt.legend()
plt.tight_layout()
plt.show()

Precio de electricidad:#

# Cargar el archivo
df = pd.read_csv("Precio_electricidad.csv")

# Corregir nombres de columnas si tienen espacios
df.columns = df.columns.str.strip()

# Convertir 'Fecha' a datetime y usar como índice
df['Fecha'] = pd.to_datetime(df['Fecha'])
df.set_index('Fecha', inplace=True)

# Ordenar por fecha por si acaso
df = df.sort_index()

plt.figure(figsize=(12, 5))
plt.plot(df.index, df['Precio'], color='navy')
plt.title("Serie de tiempo: Precio de electricidad")
plt.xlabel("Fecha")
plt.ylabel("Precio")
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()

print("Estadísticas descriptivas del precio de electricidad:")
print(df['Precio'].describe())

plt.figure(figsize=(8, 4))
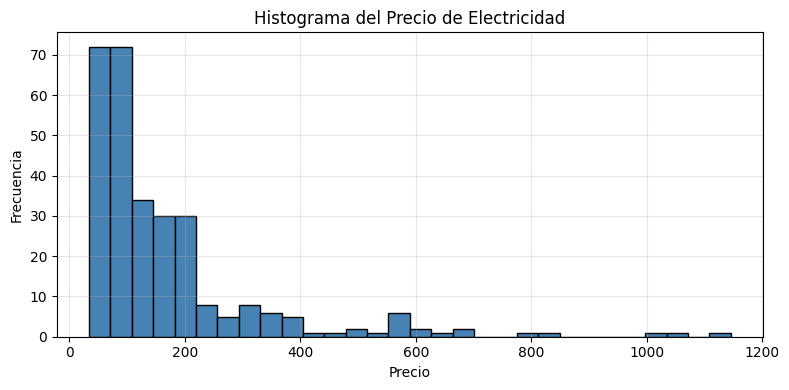
plt.hist(df['Precio'], bins=30, color='steelblue', edgecolor='black')
plt.title("Histograma del Precio de Electricidad")
plt.xlabel("Precio")
plt.ylabel("Frecuencia")
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()

Estadísticas descriptivas del precio de electricidad:
count     291.000000
mean      167.581805
std       166.627117
min        33.848903
25%        71.621639
50%       108.518182
75%       191.542964
max      1145.230988
Name: Precio, dtype: float64

import seaborn as sns

# Crear columna del mes calendario
df['mes'] = df.index.month

# Crear figura con dos subgráficos: serie de tiempo y boxplot
fig, axs = plt.subplots(1, 2, figsize=(14, 5))

# 1. Serie de tiempo
axs[0].plot(df.index, df['Precio'], color='darkblue')
axs[0].set_title("Serie de tiempo del precio de electricidad")
axs[0].set_xlabel("Fecha")
axs[0].set_ylabel("Precio")

# 2. Boxplot por mes calendario
sns.boxplot(x='mes', y='Precio', data=df, ax=axs[1])
axs[1].set_title("Distribución mensual (boxplot)")
axs[1].set_xlabel("Mes")
axs[1].set_ylabel("Precio")
axs[1].set_xticks(range(0, 12))
axs[1].set_xticklabels([
    'Ene', 'Feb', 'Mar', 'Abr', 'May', 'Jun',
    'Jul', 'Ago', 'Sep', 'Oct', 'Nov', 'Dic'
])

plt.tight_layout()
plt.show()

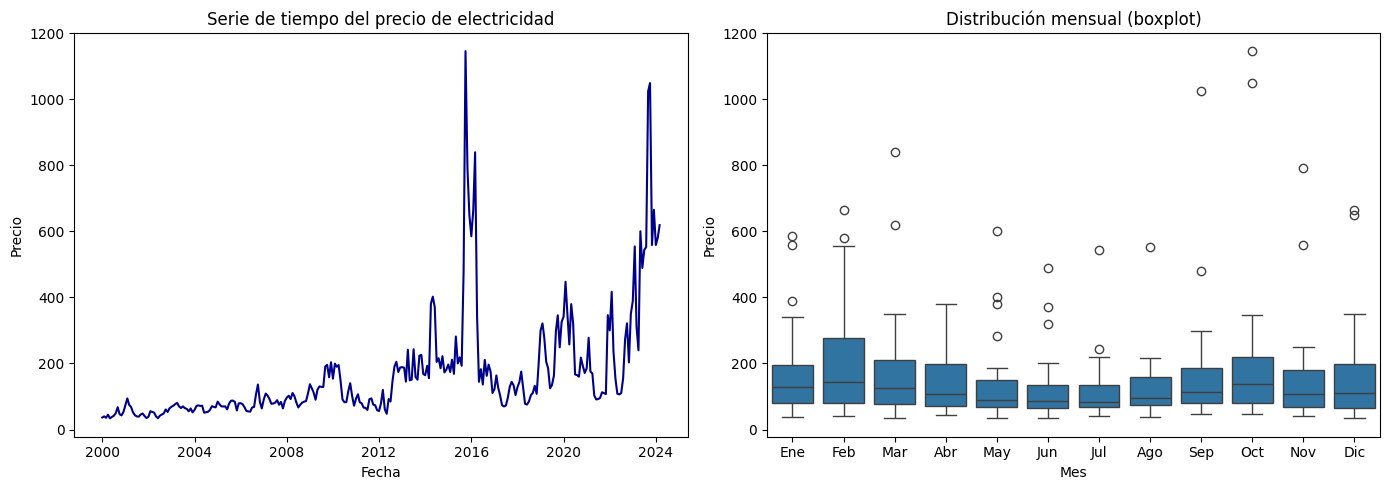
Los boxplots por mes calendario permiten observar la distribución de los valores de una serie de tiempo para cada mes a lo largo de varios años. Son especialmente útiles para identificar estacionalidad, variabilidad interanual y valores atípicos.

Descomposición aditiva:

# Descomposición aditiva con periodicidad anual (12 meses)
descomposicion_add = seasonal_decompose(df['Precio'], model='additive', period=12)

# Graficar
descomposicion_add.plot()
plt.suptitle("Descomposición Aditiva del Precio de Electricidad", fontsize=14, y=1.02)
plt.tight_layout()
plt.show()

descomposicion_mul = seasonal_decompose(df['Precio'], model='multiplicative', period=12)

# Graficar
descomposicion_mul.plot()
plt.suptitle("Descomposición Multiplicativa del Precio de Electricidad", fontsize=14, y=1.02)
plt.tight_layout()
plt.show()

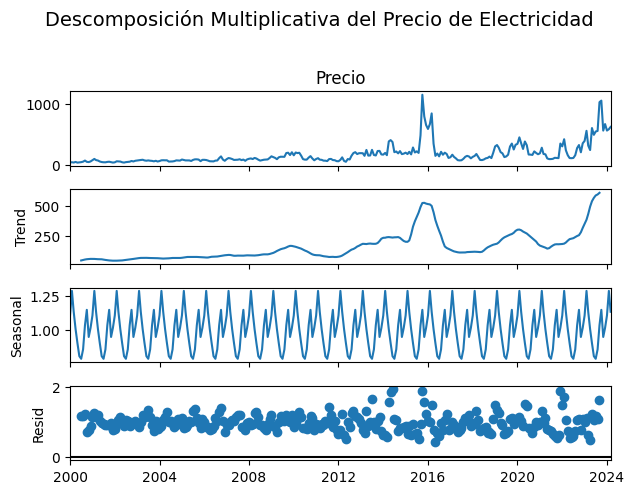
Se aplicarán nuevamente los gráficos de descomposición para analizar con mayor detalle el comportamiento de los residuos.

# Graficar
plt.figure(figsize=(10, 8))
plt.subplot(4, 1, 1)
plt.plot(descomposicion_add.observed, color="darkblue")
plt.title("Descomposición aditiva - Precio de electricidad")

plt.subplot(4, 1, 2)
plt.plot(descomposicion_add.trend, color="black")
plt.ylabel("Tendencia")

plt.subplot(4, 1, 3)
plt.plot(descomposicion_add.seasonal, color="black")
plt.ylabel("Estacionalidad")

plt.subplot(4, 1, 4)
plt.plot(descomposicion_add.resid, color="black")
plt.ylabel("Residuo")
plt.xlabel("Fecha")

plt.tight_layout()
plt.show()

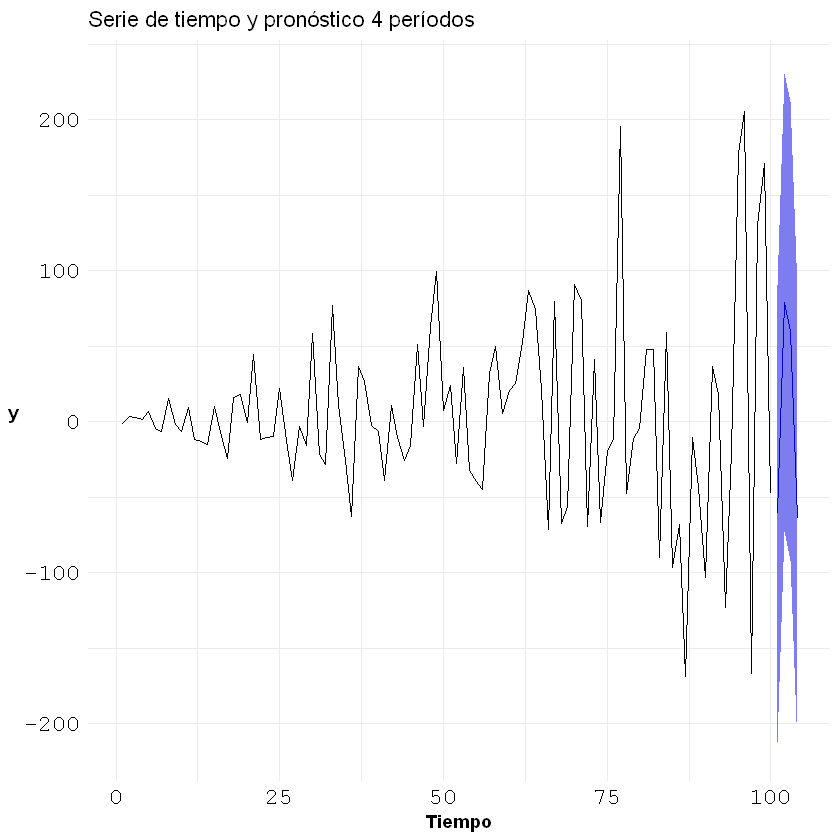
# Graficar
plt.figure(figsize=(10, 8))
plt.subplot(4, 1, 1)
plt.plot(descomposicion_mul.observed, color="darkblue")
plt.title("Descomposición aditiva - Precio de electricidad")

plt.subplot(4, 1, 2)
plt.plot(descomposicion_mul.trend, color="black")
plt.ylabel("Tendencia")

plt.subplot(4, 1, 3)
plt.plot(descomposicion_mul.seasonal, color="black")
plt.ylabel("Estacionalidad")

plt.subplot(4, 1, 4)
plt.plot(descomposicion_mul.resid, color="black")
plt.ylabel("Residuo")
plt.xlabel("Fecha")

plt.tight_layout()
plt.show()

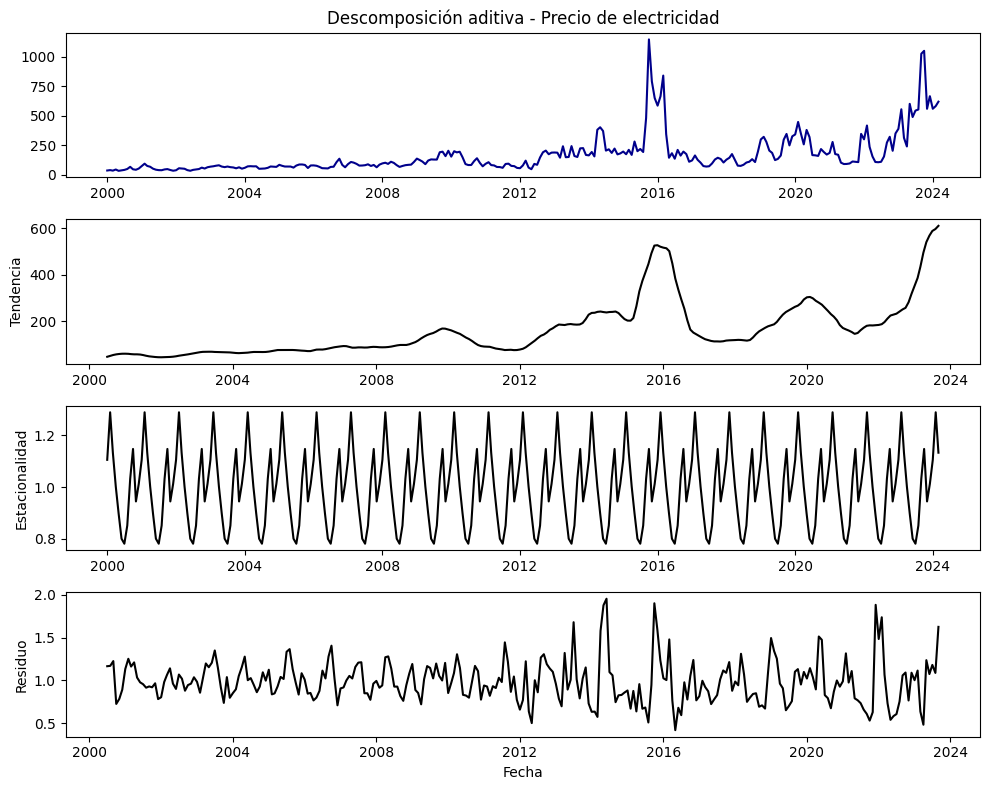
La descomposición multiplicativa resulta más apropiada para el precio de electricidad porque los residuos que genera son más estables y no presentan patrones evidentes, lo que indica un mejor aislamiento de la tendencia y la estacionalidad. Esto sugiere que la estructura proporcional de la serie ha sido capturada de forma más precisa.

Exploración visual de series de tiempo

Contents