¿Qué es una serie de tiempo?#
Las series de tiempo son colecciones de datos que varían según unidades temporales consecutivas y uniformes. Cada observación está ligada al momento en que fue registrada, y hay una sola medición por intervalo. Esto las distingue claramente de otros tipos de datos.
Por qué esto importa: el orden temporal introduce dependencia: lo que sucede hoy puede estar influenciado por lo ocurrido antes.Es una perspectiva distinta de los datos cruzados (cross‑section), donde el orden no importa en lo absoluto.
Ejemplos de series de tiempo:
Algunos ejemplos cotidianos incluyen:
Indicadores económicos, como el precio de acciones, el tipo de cambio o el PIB trimestral.
Datos climáticos, como temperatura, lluvia o niveles de CO₂.
Consumo eléctrico o tráfico web, monitoreados por hora o día.
Tasas de hospitalización o admisiones médicas que varían en el tiempo.
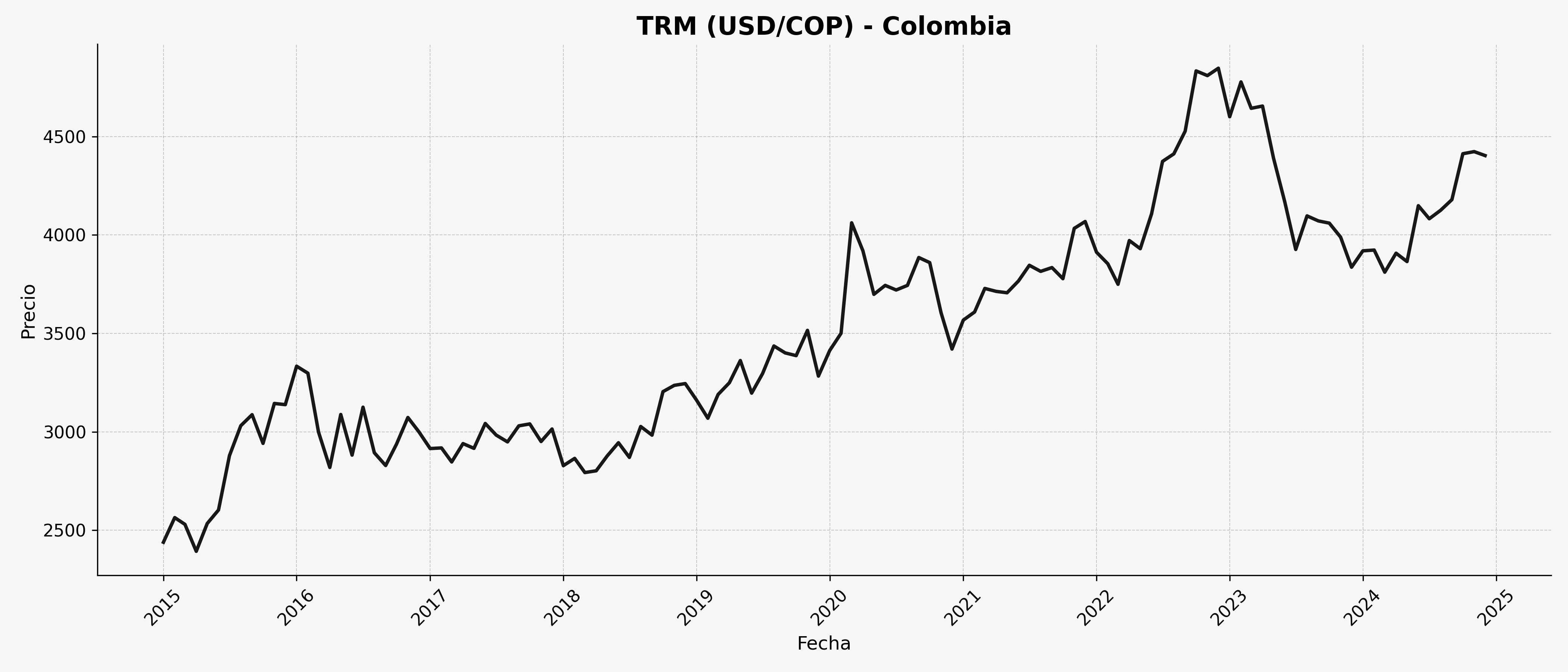
TRM#
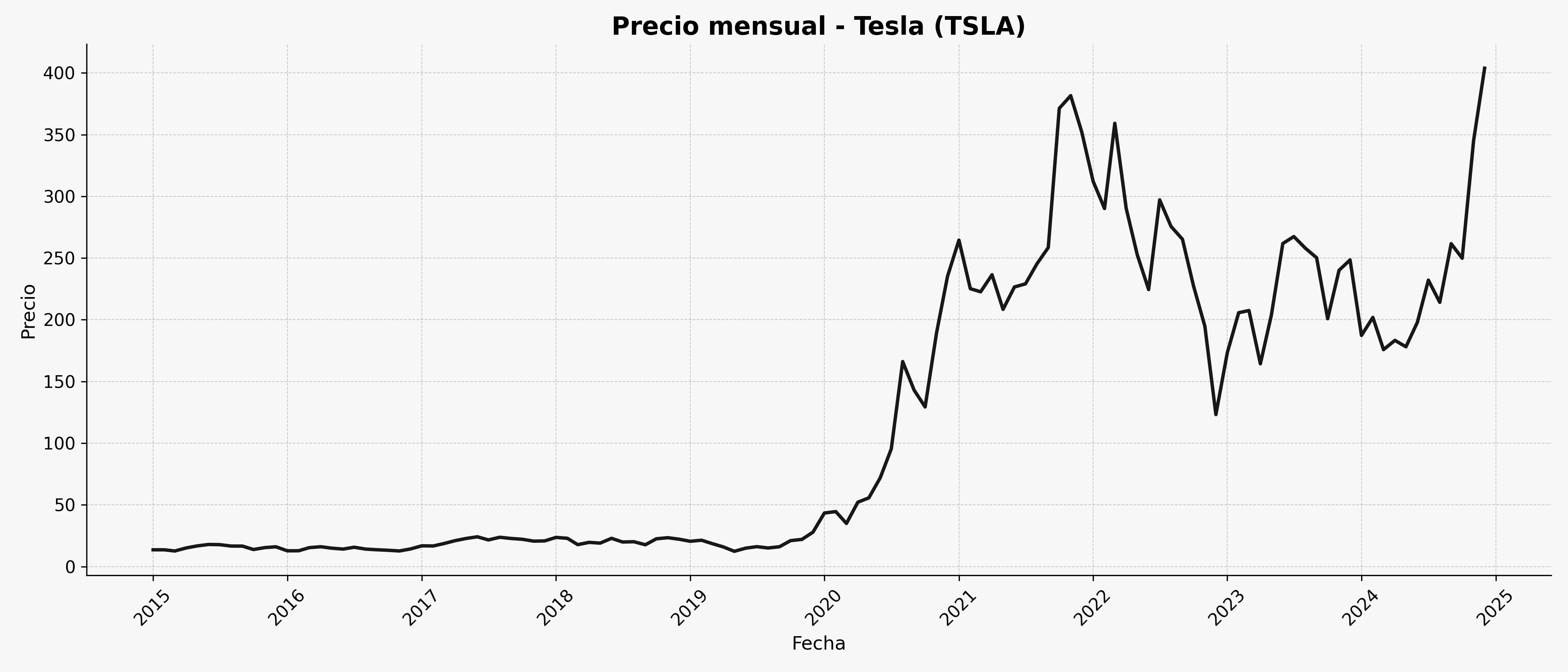
TESLA#
Componentes de las series de tiempo:#
Tendencia: curva ascendente o descendente a lo largo del tiempo.
Estacionalidad: patrones repetitivos, como picos en determinados periodos (por ejemplo, ventas decembrinas).
Ciclos: oscilaciones más amplias e irregulares que la estacionalidad.
Ruido: fluctuaciones imprevisibles y sin patrón claro.
Este tipo de visualización ayuda a entrenar el ojo desde el inicio para detectar comportamientos clave antes de pasar a los modelos formales.
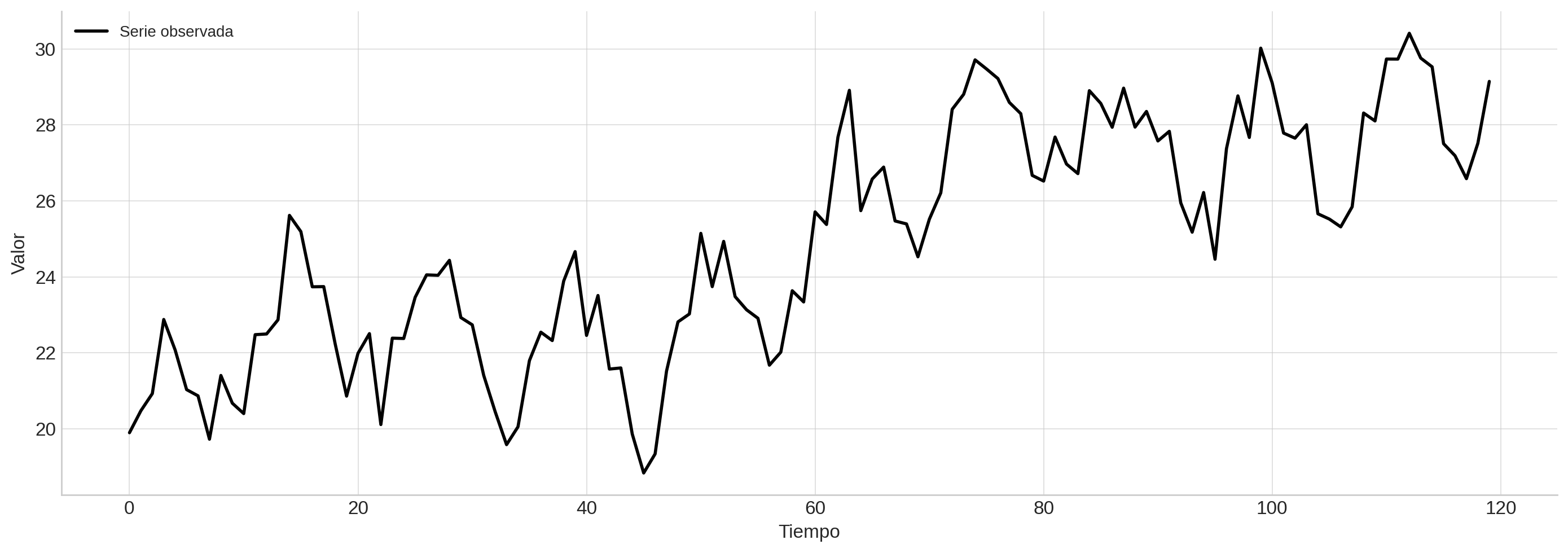
Serie#
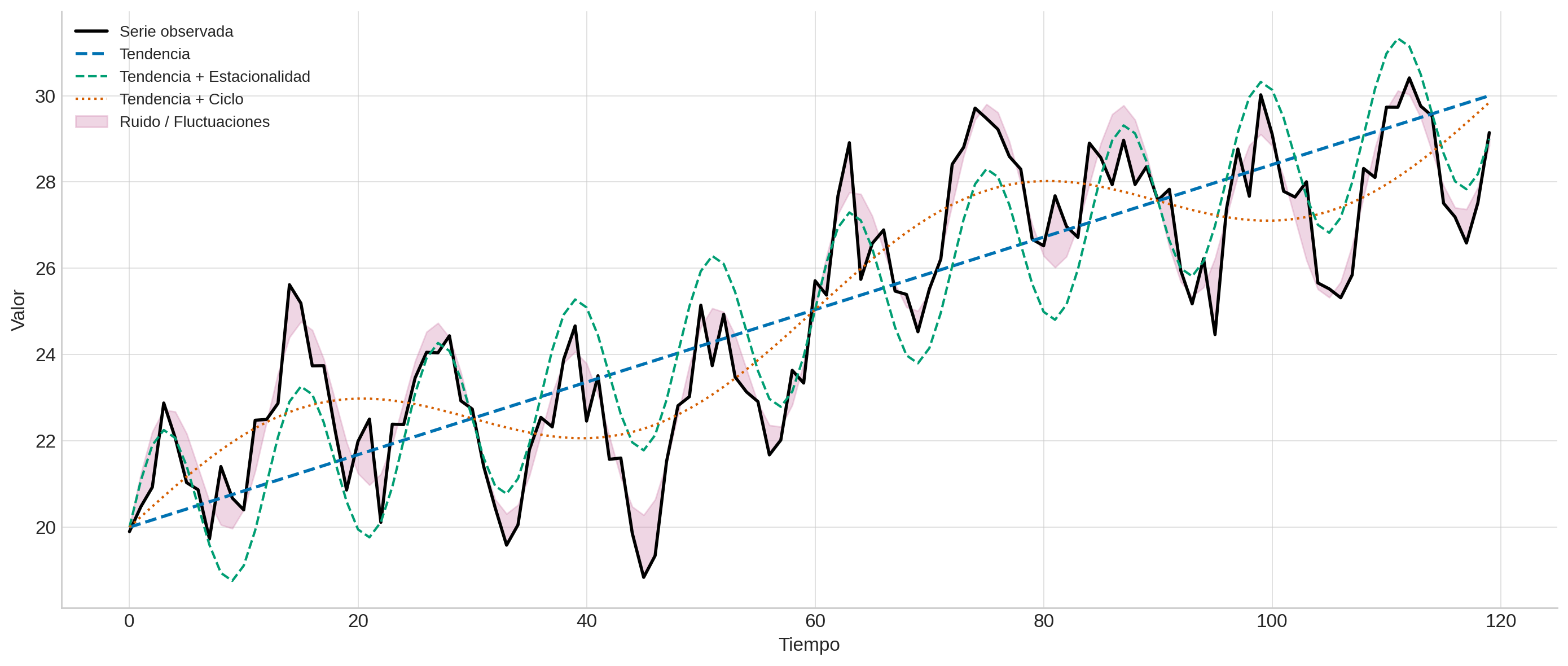
Componentes#
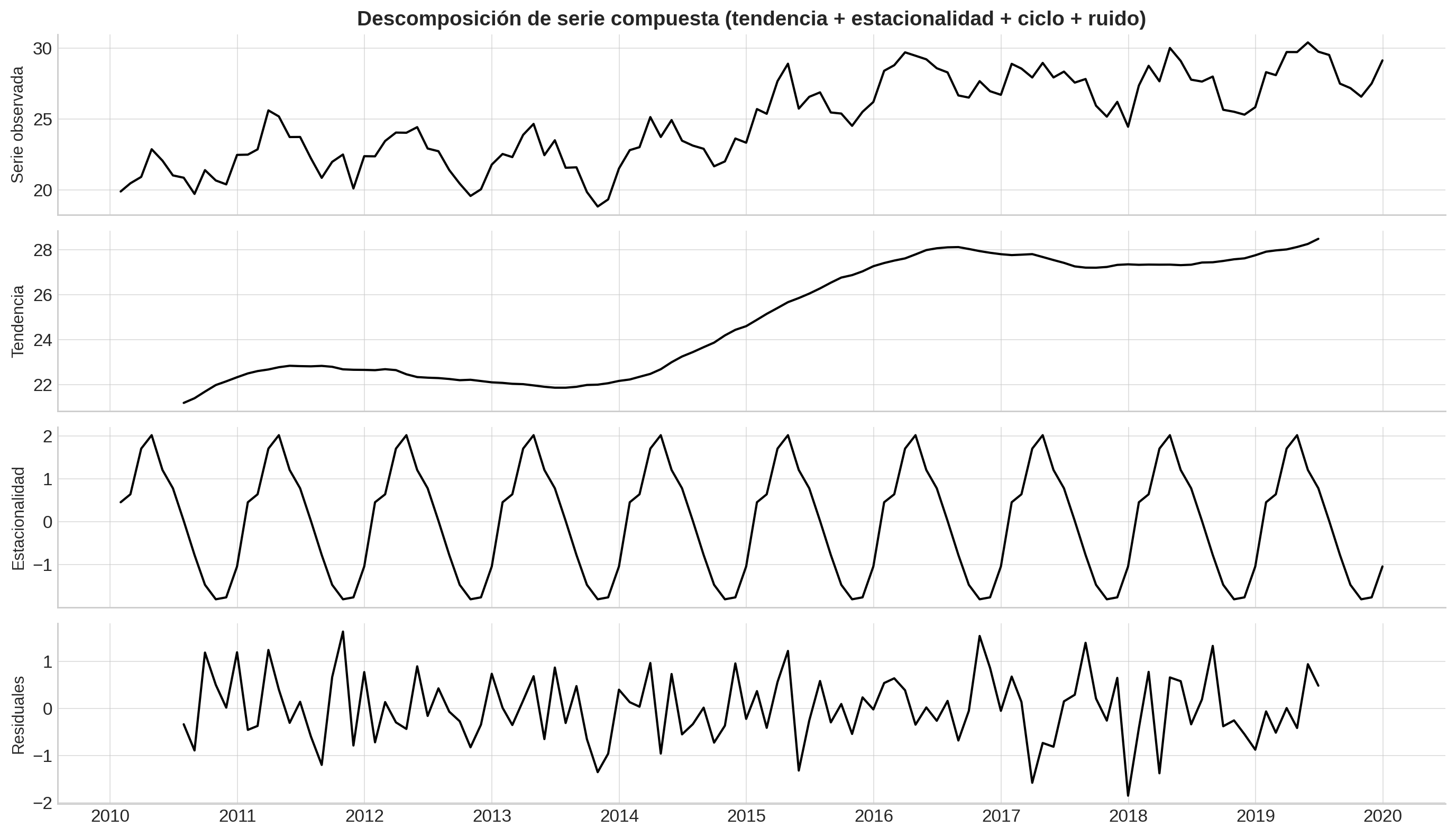
Serie_descomposición_1#
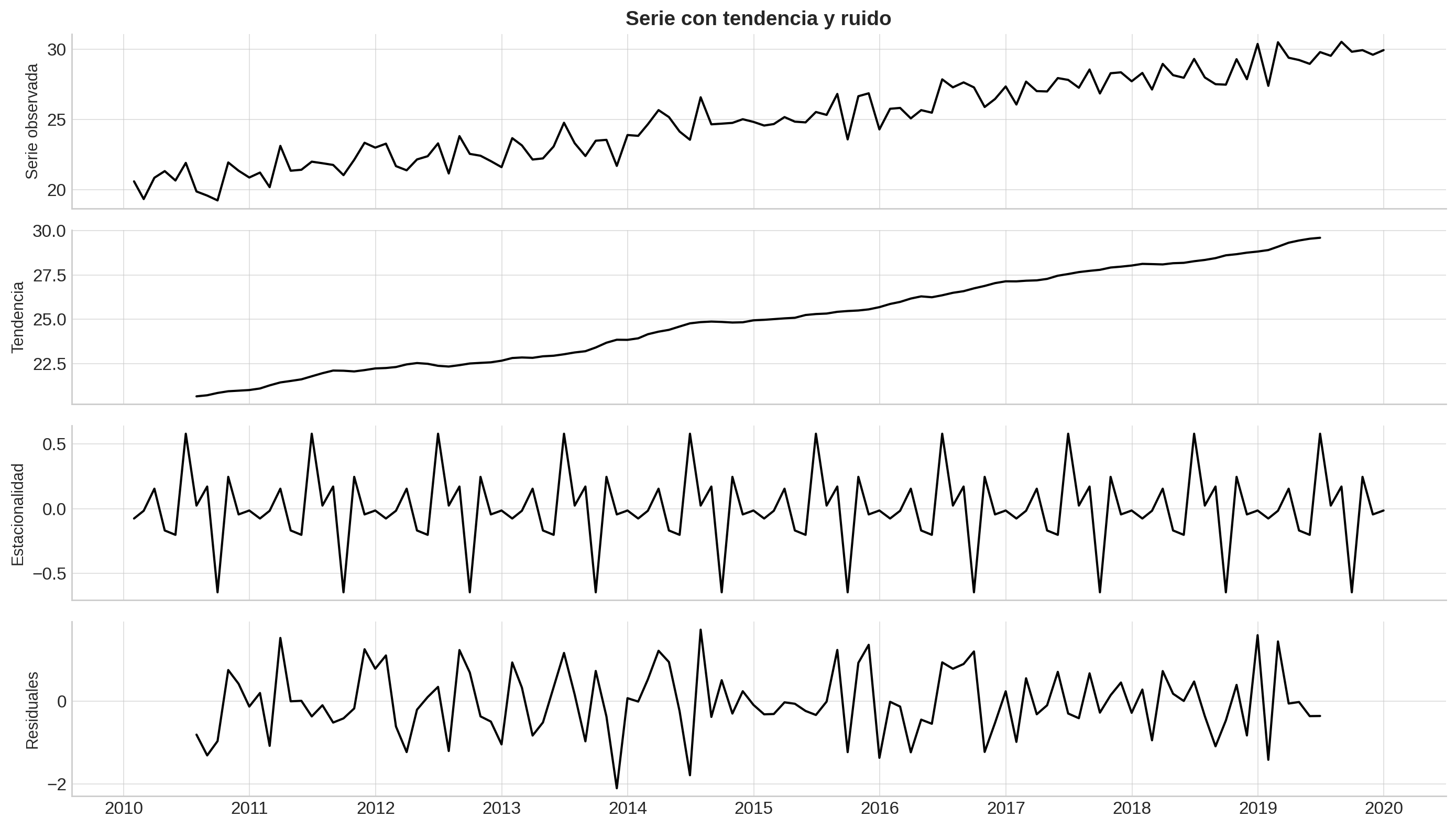
Serie_descomposición_2#
Diagnóstico visual de series de tiempo:
Este checklist te ayudará a identificar, de forma visual, los principales patrones estructurales en cualquier serie de tiempo antes de aplicar modelos.
N º |
Elemento |
¿Qué observar en el gráfico? |
|---|---|---|
1 |
Tendencia* |
¿La serie sube, baja o se mantiene estable en el tiempo? |
2 |
Esta cionalidad |
¿Se repiten patrones en intervalos fijos (meses, trimestres, años)? |
3 |
Ciclos |
¿Existen oscilaciones amplias, más largas y no necesariamente regulares? |
4 |
Ruido / Irr egularidad |
¿La serie presenta variaciones aleatorias impredecibles? |
5 |
Cambios de nivel |
¿Se observan saltos bruscos hacia arriba o abajo en algún punto del tiempo? |
6 |
Cambios en la varianza |
¿Las oscilaciones se amplían o reducen a lo largo del tiempo? |
7 |
Anomalías / Atípicos |
¿Hay puntos que se apartan fuertemente del comportamiento típico de la serie? |
8 |
Reversión a la media |
¿Después de un cambio brusco, la serie tiende a volver a un valor promedio? |
9 |
** Persistencia visual** |
¿Los valores actuales parecen estar influenciados por los anteriores? (efecto de “memoria”) |
1 0 |
Estabilidad temporal* |
¿El comportamiento de la serie es homogéneo o cambia en diferentes tramos del tiempo? |
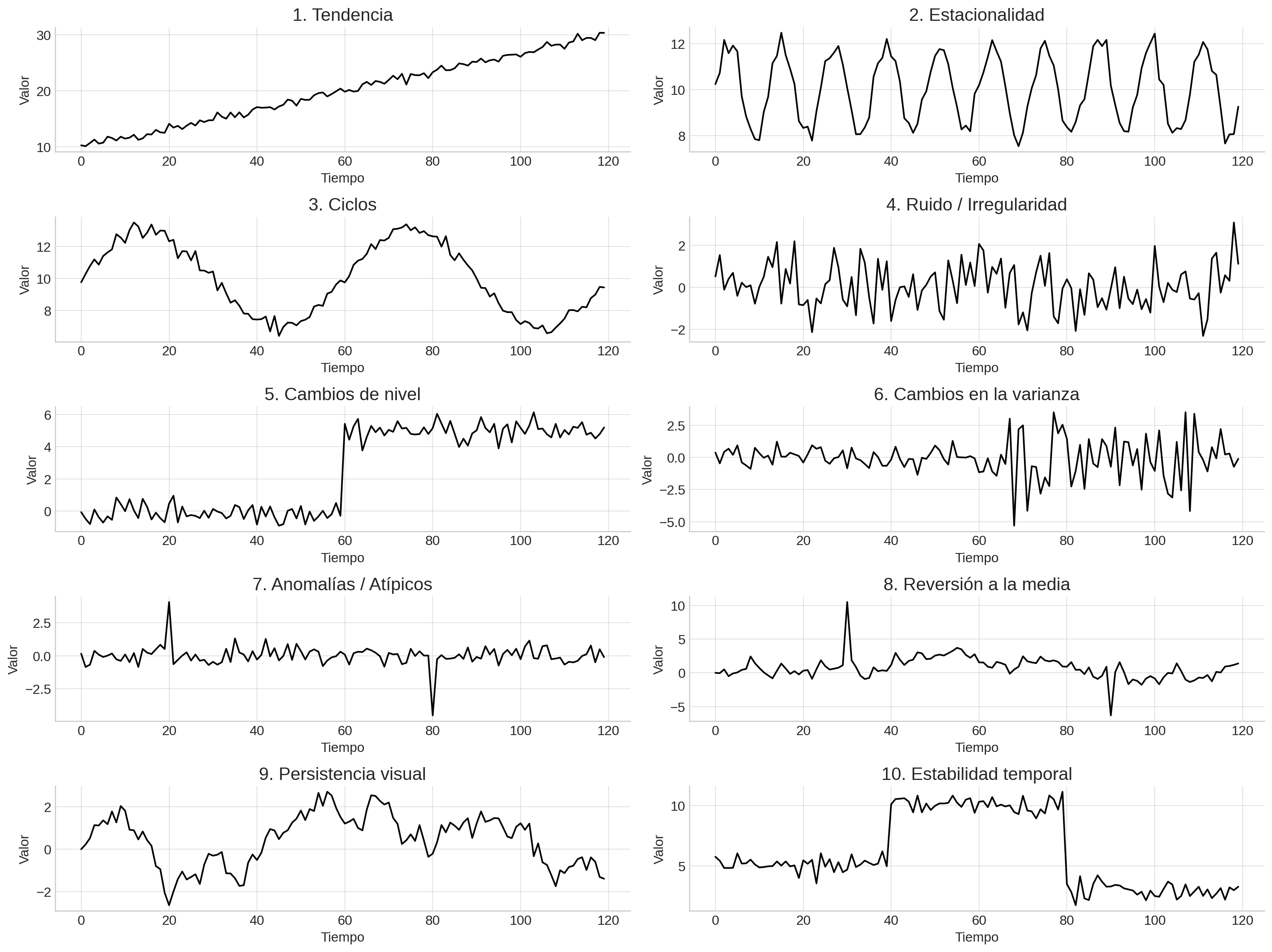
Varias_estructuras#
Identificar los patrones del checklist es como entender el terreno antes de construir: sin ese diagnóstico, cualquier modelo será una apuesta a ciegas.
Antes de ajustar cualquier modelo de series de tiempo, es fundamental detenerse a mirar la serie y entender su estructura. Un análisis visual te permite hacer un diagnóstico que te orientará sobre:
Cómo preparar la serie.
Qué tipo de modelo usar.
Cómo interpretar los resultados.
Si hay tendencia:
Tal vez necesites:
Aplicar una diferenciación (usar diferencias entre periodos) para hacer la serie estacionaria.
O usar un modelo que incorpore la tendencia explícitamente (como una regresión con tiempo o modelos ARIMA con componente de tendencia).
Si hay estacionalidad:
Es necesario usar modelos que la representen, como:
SARIMA, que incluye componentes estacionales.
Variables dummy para cada mes, trimestre, etc.
O técnicas de descomposición que separan estacionalidad y tendencia.
Si hay cambios de nivel o varianza:
Debes considerar:
Aplicar transformaciones como logaritmos o Box-Cox para estabilizar la varianza.
Detectar y modelar rupturas estructurales, con técnicas como intervención o cambio de régimen.
Si no hay estructura aparente:
Cuando solo ves ruido blanco:
No hay patrones aprovechables.
La serie es esencialmente impredecible → modelar no aporta valor.
Si hay persistencia o reversión a la media:
La persistencia visual indica autocorrelación → modelos como AR o ARIMA pueden capturarla.
La reversión a la media sugiere procesos donde la serie tiende a volver a un equilibrio → útiles en tasas de interés o precios regulados.
Métodos de descomposición:#
La descomposición permite separar una serie de tiempo en componentes estructurales más simples:
Tendencia \(T_t\): dirección general a largo plazo (creciente, decreciente o estable).
Estacionalidad \(S_t\): fluctuaciones que se repiten en intervalos regulares.
Ciclo \(C_t\): variaciones recurrentes de largo plazo, no necesariamente periódicas.
Residuo \(R_t\): ruido o variaciones impredecibles.
Tipos de descomposición:
Modelo aditivo:
Se utiliza cuando los efectos estacionales y las variaciones son constantes en magnitud, es decir, no dependen del nivel de la serie.
Común en series donde las variaciones estacionales tienen la misma amplitud a lo largo del tiempo.
Si se omite el componente cíclico (común en datos mensuales), se tiene:
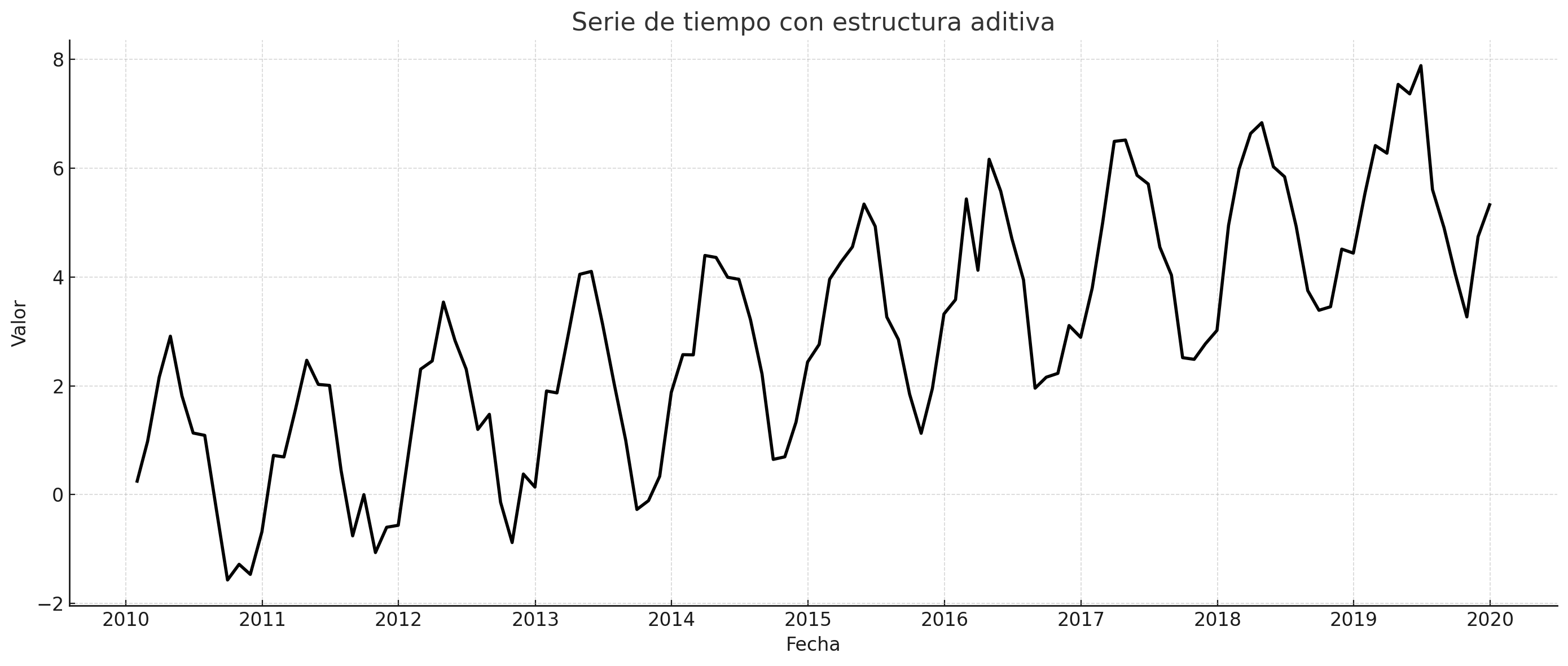
Serie_aditiva#
Modelo multiplicativo:
Se usa cuando los efectos estacionales y la variabilidad aumentan o disminuyen proporcionalmente con la tendencia.
Es adecuado para series donde la estacionalidad se amplifica con el crecimiento.
La versión sin componente cíclico:
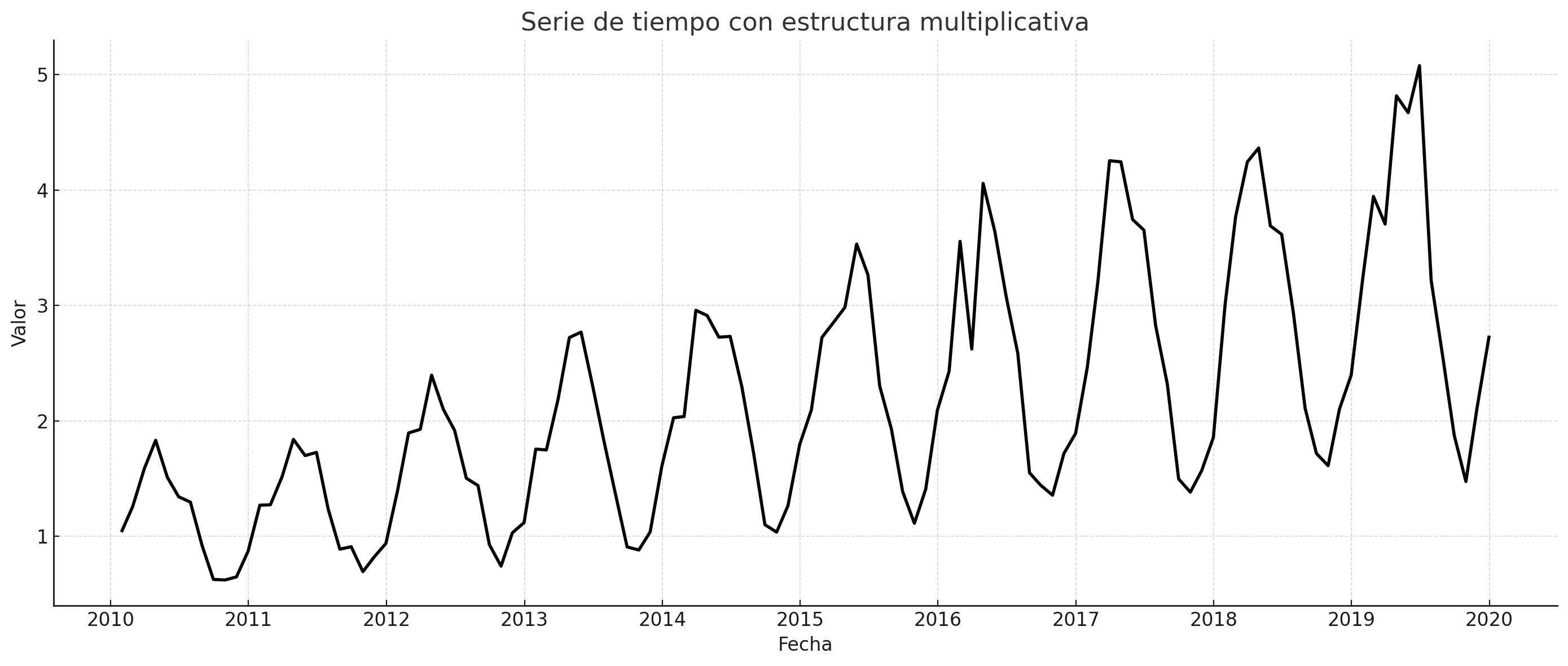
Serie_multiplicativa#
Descomposición#
Elección entre modelos:
Observación en la serie |
Tipo de modelo |
|---|---|
Estacionalidad de amplitud constante |
Aditivo |
Estacionalidad que crece/disminuye con la tendencia |
Multiplicativo |
Varianza constante |
Aditivo |
Varianza que cambia con el nivel de la serie |
Multiplicativo |
¿Por qué descomponer?
Entender la estructura: identificar qué mueve la serie.
Preparar para modelar: eliminar tendencia/estacionalidad para aplicar modelos como ARIMA.
Interpretar fenómenos: observar por separado cómo influye la tendencia, el ciclo o el patrón estacional.
Ejemplos#
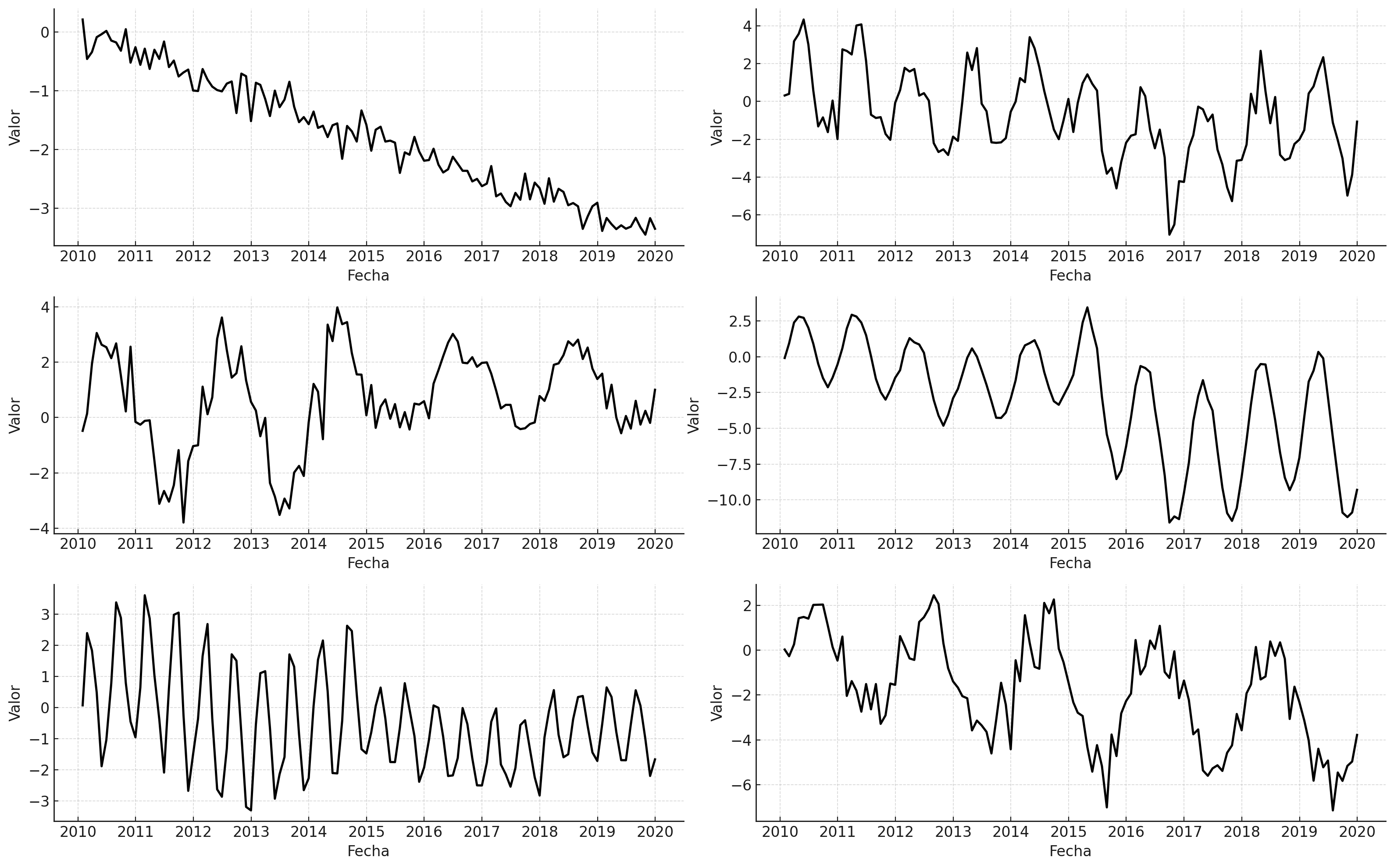
Ejemplos#