Ejemplo métricas de desempeño Desempleo

Ejemplo métricas de desempeño Desempleo#

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt

# Cargar el archivo xlsx:
df = pd.read_excel('Desempleo.xlsx')

# Corregir nombres de columnas si tienen espacios
df.columns = df.columns.str.strip()

df.head()
Fecha Desempleo
0 2001-01-01 16.622326
1 2001-02-01 17.434206
2 2001-03-01 15.811933
3 2001-04-01 14.515078
4 2001-05-01 14.035833 
# Convertir 'Fecha' a datetime y usar como índice
df['Fecha'] = pd.to_datetime(df['Fecha'])
df.set_index('Fecha', inplace=True)

# Ordenar por fecha por si acaso
df = df.sort_index()

# Establecer frecuencia explícita para evitar el warning de statsmodels
df.index.freq = df.index.inferred_freq

plt.figure(figsize=(12, 5))
plt.plot(df, color='navy')
plt.title("Serie de tiempo: Desempleo")
plt.xlabel("Fecha")
plt.ylabel("Valor")
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
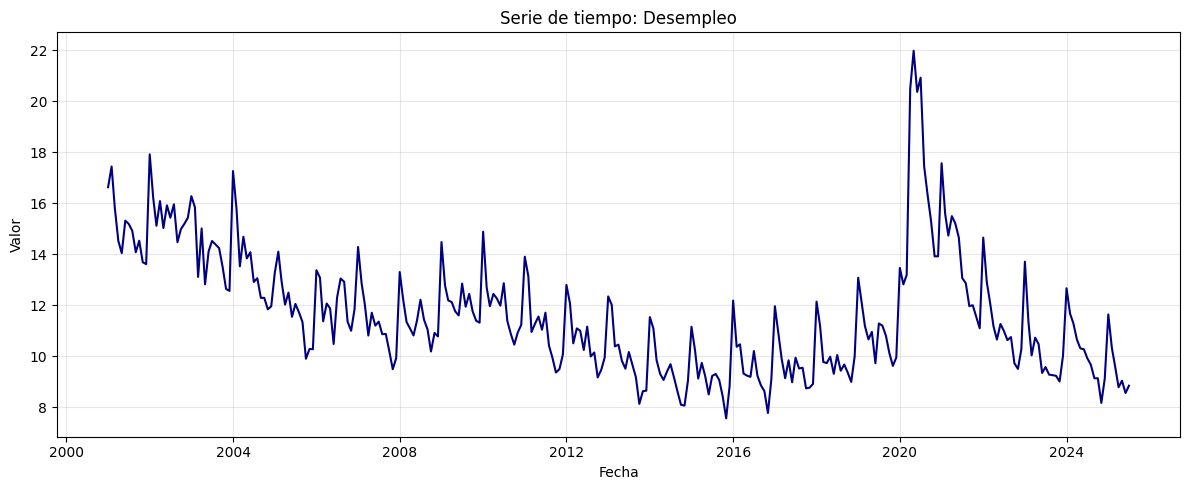
../../_images/output_4_010.png 
serie = df.loc[:'2019-12-31']

plt.figure(figsize=(12, 5))
plt.plot(serie, color='navy')
plt.title("Serie de tiempo: Desempleo hasta 2019")
plt.xlabel("Fecha")
plt.ylabel("Valor")
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
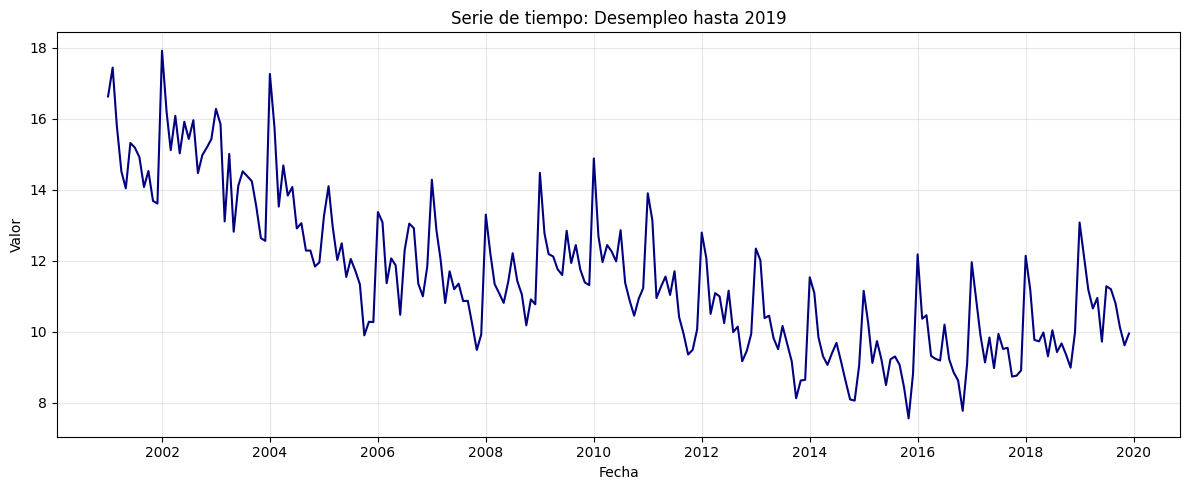
../../_images/output_5_05.png

Conjunto de train y test:#

# Dividir en train y test (por ejemplo, 80% train, 20% test)
split = int(len(serie) * 0.8)
train, test = serie[:split], serie[split:]

# Graficar train y test:

plt.figure(figsize=(12, 5))
plt.plot(train, label='Train', color='navy')
plt.plot(test, label='Test', color='orange')
plt.title("Conjunto de train y test")
plt.xlabel("Fecha")
plt.ylabel("Valor")
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
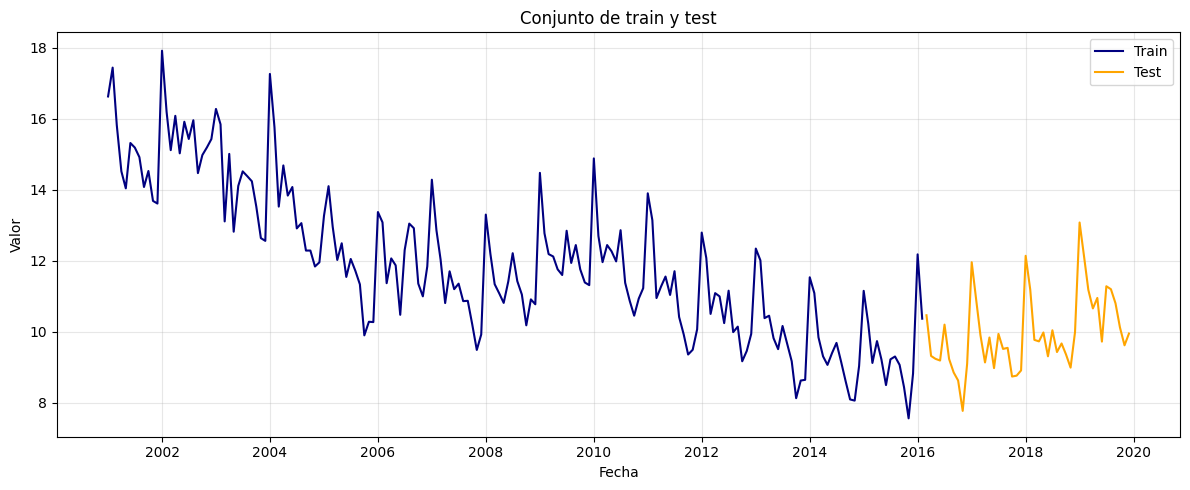
../../_images/output_7_012.png

Ajuste métodos de suavizamiento:#

from statsmodels.tsa.holtwinters import SimpleExpSmoothing, Holt, ExponentialSmoothing
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error, max_error, explained_variance_score

# Ajustar modelos de suavizamiento
# a) Simple Exponential Smoothing
model_ses = SimpleExpSmoothing(train).fit(optimized=True)
y_train_pred_ses = model_ses.fittedvalues
y_pred_test_ses = model_ses.forecast(len(test))

# b) Holt (Doble suavizamiento)
model_holt = Holt(train).fit(optimized=True)
y_train_pred_holt = model_holt.fittedvalues
y_pred_test_holt = model_holt.forecast(len(test))

# c) Holt-Winters (Triple suavizamiento, aditivo, estacionalidad anual si mensual)
estacionalidad = 12 if train.index.freqstr in ['M', 'MS'] else None
model_hw = ExponentialSmoothing(train, trend='add', seasonal='add', seasonal_periods=estacionalidad).fit(optimized=True)
y_train_pred_hw = model_hw.fittedvalues
y_pred_test_hw = model_hw.forecast(len(test))

# Graficar los ajustes y predicciones
plt.figure(figsize=(12, 5))
plt.plot(serie, label='Serie original', color='black')
plt.plot(y_train_pred_ses, label='SES - Ajuste', color='dodgerblue')
plt.plot(y_train_pred_holt, label='Holt - Ajuste', color='green')
plt.plot(y_train_pred_holt, label='HW - Ajuste', color='orange')
plt.plot(test.index, y_pred_test_ses, label='SES - Pronóstico', ls='--', color='blue')
plt.plot(test.index, y_pred_test_holt, label='Holt - Pronóstico', ls='--', color='green')
plt.plot(test.index, y_pred_test_hw, label='HW - Pronóstico', ls='--', color='orange')
plt.legend()
plt.title('Ajuste y Pronóstico con Métodos de Suavizamiento')
plt.show()
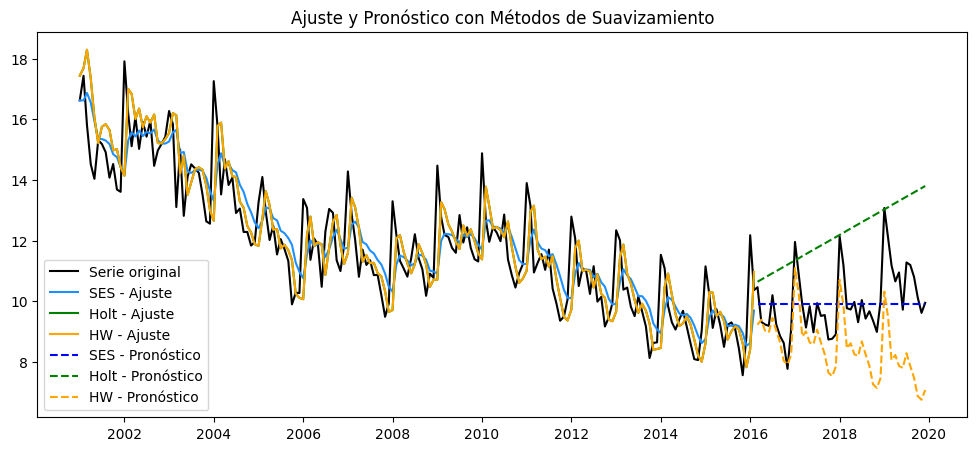
../../_images/output_10_012.png

Métricas de desempeño:#

from sklearn.metrics import (
    r2_score, mean_absolute_error, mean_squared_error,
    max_error, mean_absolute_percentage_error, explained_variance_score
)

# Función para calcular todas las métricas
def calcular_metricas(y_true, y_pred):
    metrics = {}
    metrics['R2'] = r2_score(y_true, y_pred)
    metrics['MAE'] = mean_absolute_error(y_true, y_pred)
    metrics['MSE'] = mean_squared_error(y_true, y_pred)
    metrics['RMSE'] = np.sqrt(metrics['MSE'])
    # Evitar división por cero en MAPE:
    metrics['MAPE'] = mean_absolute_percentage_error(y_true, y_pred) if np.max(np.abs(y_true)) > 0 else 0
    metrics['Max Error'] = max_error(y_true, y_pred)
    metrics['Explained Variance'] = explained_variance_score(y_true, y_pred)
    return metrics

# Calcular métricas en train para cada modelo
metrics_ses_train = calcular_metricas(train, y_train_pred_ses)
metrics_holt_train = calcular_metricas(train, y_train_pred_holt)
metrics_hw_train = calcular_metricas(train, y_train_pred_hw)

# Calcular métricas en Test para cada modelo
metrics_ses = calcular_metricas(test, y_pred_test_ses)
metrics_holt = calcular_metricas(test, y_pred_test_holt)
metrics_hw = calcular_metricas(test, y_pred_test_hw)

# Mostrar resultados en tabla para train:
resultados_train = pd.DataFrame({
    "SES": metrics_ses_train,
    "Holt": metrics_holt_train,
    "Holt-Winters": metrics_hw_train
})
print("Métricas de desempeño en el conjunto de train:")
display(resultados_train)

# Mostrar resultados en tabla para test:
resultados = pd.DataFrame({
    "SES": metrics_ses,
    "Holt": metrics_holt,
    "Holt-Winters": metrics_hw
})
print("\nMétricas de desempeño en el conjunto de test:")
display(resultados)

Métricas de desempeño en el conjunto de train:
SES Holt Holt-Winters
R2 0.714503 0.668827 0.928334
MAE 0.849031 0.870869 0.443224
MSE 1.320914 1.532241 0.331577
RMSE 1.149310 1.237837 0.575828
MAPE 0.071564 0.071801 0.036452
Max Error 3.944624 4.603243 1.776734
Explained Variance 0.717751 0.671016 0.928334 
Métricas de desempeño en el conjunto de test:
SES Holt Holt-Winters
R2 -0.003979 -4.633574 -1.857950
MAE 0.808906 2.287011 1.491747
MSE 1.125912 6.317770 3.205047
RMSE 1.061090 2.513518 1.790265
MAPE 0.079579 0.238254 0.145455
Max Error 3.177836 4.111111 3.333760
Explained Variance 0.000000 -0.085371 0.101232

Interpretación y análisis

  • Holt-Winters logra el mejor ajuste en el conjunto de entrenamiento, con un \(R^2 = 0.928\) y los valores más bajos de MAE y RMSE. Esto indica que el modelo capta muy bien la tendencia y estacionalidad de la serie en los datos históricos.

  • SES y Holt tienen un \(R^2\) menor (\(\approx 0.71\) y \(\approx 0.67\) respectivamente) y errores más altos, lo que sugiere que capturan menos estructura, especialmente la estacionalidad.

En el conjunto de prueba (test), el desempeño de todos los modelos cae significativamente:

  • Todos los modelos presentan valores negativos de \(R^2\), lo cual significa que son peores que simplemente predecir la media de la serie.

  • El SES, aunque es el modelo más simple, presenta el menor MAE (\(0.81\)) y el menor MAPE (\(0.079\)) en test.

  • Holt-Winters, a pesar de ser el mejor en entrenamiento, incrementa sus errores en test (MAE de \(1.49\), MAPE de \(0.145\)), reflejando un posible sobreajuste (overfitting).

  • Holt tiene el peor desempeño en test, con un MAE de \(2.28\) y un MAPE de \(0.238\).

  • El Max Error es alto en todos los modelos en test, lo cual evidencia que pueden cometer errores grandes en ciertos puntos.

  • El Explained Variance también cae a valores cercanos o inferiores a cero, mostrando poca capacidad explicativa fuera de la muestra.

Conclusión

Estos resultados muestran que los modelos de suavizamiento pueden ajustar muy bien los datos históricos, pero su capacidad para predecir fuera de muestra puede ser limitada, especialmente si la serie de tiempo presenta cambios de comportamiento, shocks o alta variabilidad.

Contents