Prueba ADF (Augmented Dickey-Fuller)#
La prueba ADF es una de las herramientas más utilizadas para determinar si una serie de tiempo es estacionaria. Su propósito es verificar si la serie tiene una raíz unitaria, lo que implicaría no estacionariedad.
Hipótesis de la prueba
Hipótesis nula (\(H_0\)): La serie tiene una raíz unitaria → no estacionaria
Hipótesis alternativa (\(H_1\)): La serie no tiene raíz unitaria → estacionaria
Modelo base
La prueba ADF se basa en estimar la siguiente regresión:
donde:
\(\Delta y_t = y_t - y_{t-1}\) es la primera diferencia de la serie
\(t\) es una tendencia determinista (opcional)
\(p\) es el número de rezagos incluidos (para controlar autocorrelación)
\(\gamma\) es el parámetro clave para evaluar la presencia de una raíz unitaria
\(\varepsilon_t\) es un término de error (ruido blanco)
¿Qué evalúa la prueba?
El valor clave es el coeficiente \(\gamma\) asociado a \(y_{t-1}\) en la regresión.
Si \(\gamma = 0\), entonces la ecuación se convierte en:
\[\Delta y_t = \alpha + \beta t + \sum \delta_i \Delta y_{t-i} + \varepsilon_t\]→ Lo que implica que la serie tiene una raíz unitaria (es un random walk), y por tanto no es estacionaria.
Si \(\gamma < 0\), entonces el término \(y_{t-1}\) fuerza un retorno al promedio, lo cual es consistente con una serie estacionaria.
¿Por qué el estadístico ADF da negativo?
Cuando se estima \(\gamma\) y se calcula el estadístico de prueba ADF, este suele ser negativo porque estamos evaluando si \(\gamma < 0\).
Cuanto más negativo sea el valor, más evidencia existe contra la hipótesis nula (no estacionaria).
Valor p y decisión estadística
La prueba devuelve un valor p que indica la probabilidad de obtener un estadístico como el observado, asumiendo que la hipótesis nula es cierta.
Si \(p < 0.05\), se rechaza \(H_0\) → no hay raíz unitaria → la serie es estacionaria.
Si \(p \geq 0.05\), no se rechaza \(H_0\) → no hay evidencia suficiente para afirmar estacionariedad → la serie podría no ser estacionaria.
Tipos de modelos en la prueba ADF
Dependiendo de la naturaleza de la serie, se pueden evaluar diferentes variantes del modelo ADF:
Sin constante ni tendencia:
\[\Delta y_t = \gamma y_{t-1} + \sum \delta_i \Delta y_{t-i} + \varepsilon_t\]Con constante:
\[\Delta y_t = \alpha + \gamma y_{t-1} + \sum \delta_i \Delta y_{t-i} + \varepsilon_t\]Con constante y tendencia:
\[\Delta y_t = \alpha + \beta t + \gamma y_{t-1} + \sum \delta_i \Delta y_{t-i} + \varepsilon_t\]
La elección depende de si se sospecha que la serie tiene tendencia determinista o simplemente nivel constante.
Resumen:
Se estima una regresión en primeras diferencias con \(y_{t-1}\) como regresor.
Se evalúa si \(\gamma < 0\) de forma significativa.
El estadístico ADF negativo refleja el valor estimado de \(\gamma\).
El valor p indica si ese resultado es estadísticamente significativo.
Criterios de interpretación
Resultado ADF |
Valor p |
Conclusión |
|---|---|---|
Muy negativo |
\(< 0.05\) |
Rechazar \(H_0\) → Estacionaria |
Cercano a 0 |
\(\geq 0.05\) |
No rechazar \(H_0\) → No estacionaria |
Analog_resorte#
Se podría afirmar que una serie es estacionaria si \(y_{t-1}\) ayuda a predecir la variación siguiente de la serie de tiempo (\(\Delta y_t\)).
Lo que hace la prueba es verificar si \(y_{t-1}\) aporta información significativa para predecir \(\Delta y_t\).
Si \(y_{t-1}\) no tiene ningún efecto sobre \(\Delta y_t\) (es decir, \(\gamma = 0\)), la serie tiene una raíz unitaria → no es estacionaria.
Si \(y_{t-1}\) sí tiene un efecto negativo (es decir, \(\gamma < 0\) y significativo), la serie tiende a corregirse, lo que indica estacionariedad.
Interpretación económica
Cuando \(y_{t-1}\) ayuda a predecir la dirección y magnitud del cambio futuro:
Si \(y_{t-1}\) es alto, \(\Delta y_t\) tiende a ser negativo → la serie baja.
Si \(y_{t-1}\) es bajo, \(\Delta y_t\) tiende a ser positivo → la serie sube.
Esto indica que la serie tiene fuerza de retorno al promedio → propiedad típica de una serie estacionaria.
Observación:
Que \(y_{t-1}\) ayude a predecir \(\Delta y_t\) no es una definición general de estacionariedad, sino una forma práctica de evaluarla bajo el modelo autorregresivo en primera diferencia.
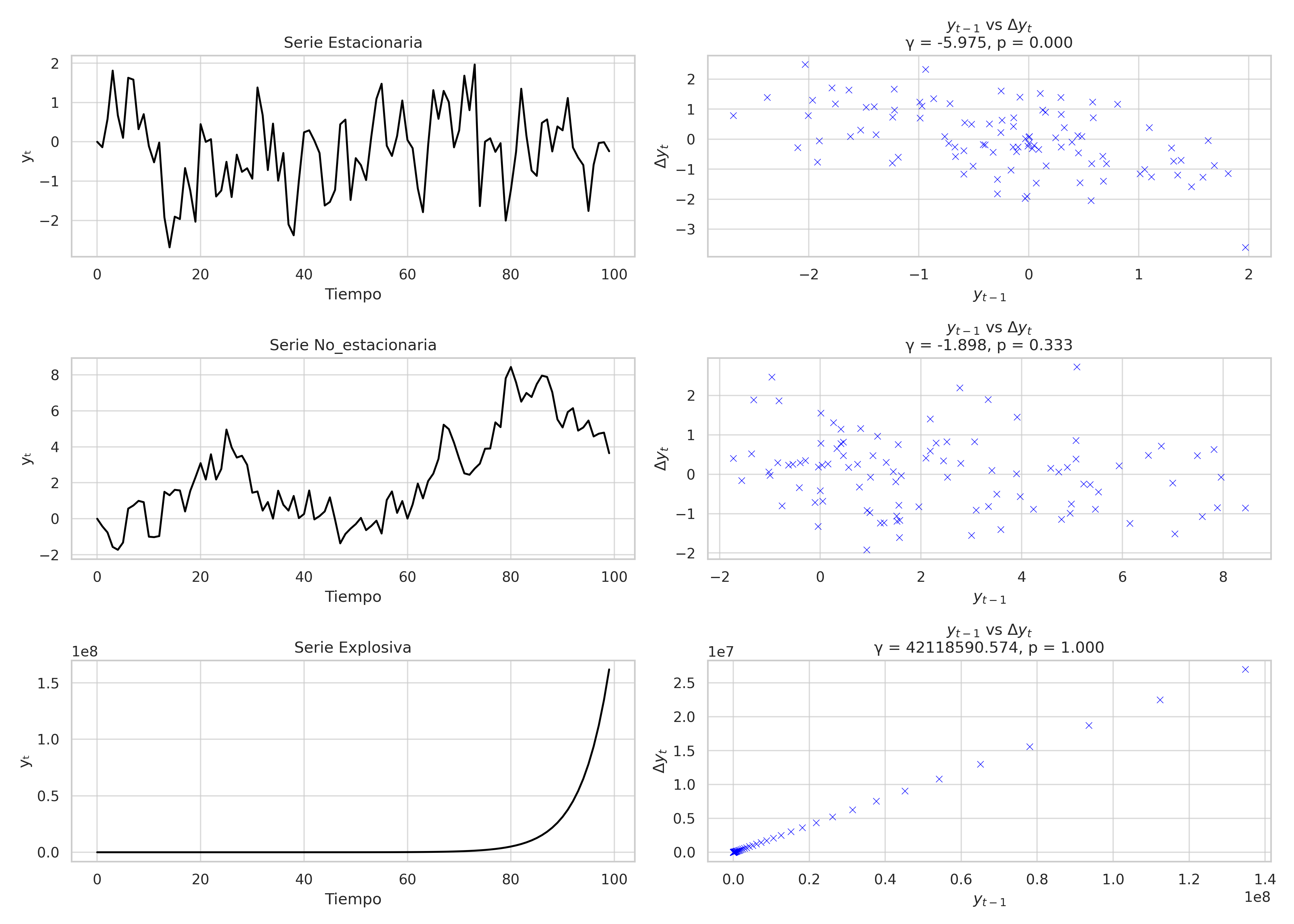
series_adf_visual_examples#
Código Pyhton para prueba ADF:#
Irradiancia Medellín:#
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
# Cargar el archivo xlsx:
df = pd.read_excel('Irradiancia Medellín.xlsx')
# Corregir nombres de columnas si tienen espacios
df.columns = df.columns.str.strip()
# Convertir 'Fecha' a datetime y usar como índice
df['Fecha'] = pd.to_datetime(df['Fecha'])
df.set_index('Fecha', inplace=True)
# Ordenar por fecha por si acaso
df = df.sort_index()
# Establecer frecuencia explícita para evitar el warning de statsmodels
df.index.freq = df.index.inferred_freq
plt.figure(figsize=(18, 5))
plt.plot(df, color='navy')
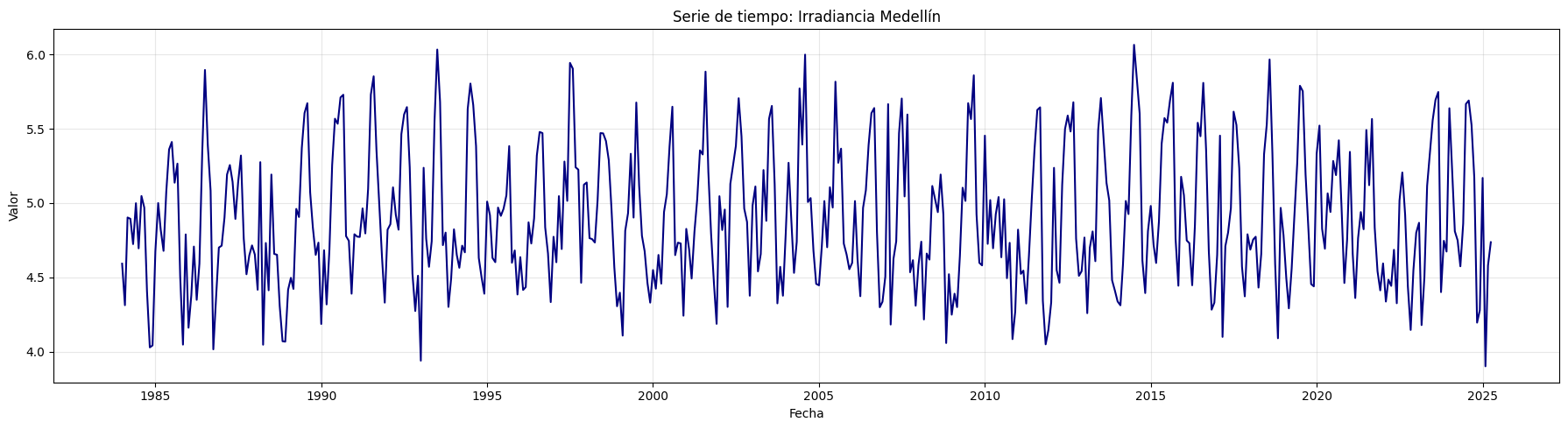
plt.title("Serie de tiempo: Irradiancia Medellín")
plt.xlabel("Fecha")
plt.ylabel("Valor")
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
Opción regression en la prueba ADF
Cuando aplicamos la prueba ADF en Python con adfuller, el argumento
regression nos permite indicar qué términos incluir en la regresión
auxiliar. Las opciones disponibles son:
O p c i ó n |
Componentes incluidos |
Descripción |
Cuándo usarla |
|---|---|---|---|
n |
Ninguno |
No incluye constante ni tendencia |
Cuando se espera que la serie fluctúe alrededor de cero |
c |
Constante (por defecto) |
Incluye solo el intercepto (media distinta de cero) |
Cuando la serie no tiene tendencia, pero sí una media estable |
c t |
Constante + tendencia lineal |
Incluye intercepto y pendiente lineal |
Cuando la serie muestra una tendencia lineal creciente o decreciente |
c t t |
Constante + tendencia lineal + cuadrática |
Intercepto, pendiente y curvatura (forma parabólica) |
Cuando la serie presenta una aceleración o desaceleración clara |
Regresión
"n": Ruido blanco sin media ni tendenciaRegresión
"c": Serie con media distinta de ceroRegresión
"ct": Serie con tendencia lineal claraRegresión
"ctt": Serie con tendencia cuadrática (curvatura)
Recomendaciones prácticas:
Siempre inspecciona visualmente la serie antes de elegir la opción de regresión.
Si tienes dudas, compara resultados con
"c"y"ct".Incluir pocos términos cuando hay una tendencia puede llevar a errores tipo II (falsos negativos).
Incluir demasiados términos cuando no son necesarios puede reducir la potencia del test.
from statsmodels.tsa.stattools import adfuller
adf_result = adfuller(df, regression='c')
print(f'Estadístico ADF: {adf_result[0]}')
print(f'Valor p: {adf_result[1]}')
# Interpretación del resultado
alpha = 0.05
if adf_result[1] < alpha:
print("Rechazamos la hipótesis nula: La serie es estacionaria.")
else:
print("No podemos rechazar la hipótesis nula: La serie no es estacionaria.")
Estadístico ADF: -5.629217000672
Valor p: 1.0992990513356142e-06
Rechazamos la hipótesis nula: La serie es estacionaria.
Temperatura Medellín:#
# Cargar el archivo xlsx:
df = pd.read_excel('Temperatura Medellín.xlsx')
# Corregir nombres de columnas si tienen espacios
df.columns = df.columns.str.strip()
# Convertir 'Fecha' a datetime y usar como índice
df['Fecha'] = pd.to_datetime(df['Fecha'])
df.set_index('Fecha', inplace=True)
# Ordenar por fecha por si acaso
df = df.sort_index()
# Establecer frecuencia explícita para evitar el warning de statsmodels
df.index.freq = df.index.inferred_freq
plt.figure(figsize=(18, 5))
plt.plot(df, color='navy')
plt.title("Serie de tiempo: Temperatura Medellín")
plt.xlabel("Fecha")
plt.ylabel("Valor")
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
adf_result = adfuller(df, regression='c')
print(f'Estadístico ADF: {adf_result[0]}')
print(f'Valor p: {adf_result[1]}')
# Interpretación del resultado
alpha = 0.05
if adf_result[1] < alpha:
print("Rechazamos la hipótesis nula: La serie es estacionaria.")
else:
print("No podemos rechazar la hipótesis nula: La serie no es estacionaria.")
Estadístico ADF: -3.8256858465908485
Valor p: 0.002655181395794914
Rechazamos la hipótesis nula: La serie es estacionaria.
Desempleo:#
# Cargar el archivo xlsx:
df = pd.read_excel('Desempleo.xlsx')
# Corregir nombres de columnas si tienen espacios
df.columns = df.columns.str.strip()
# Convertir 'Fecha' a datetime y usar como índice
df['Fecha'] = pd.to_datetime(df['Fecha'])
df.set_index('Fecha', inplace=True)
# Ordenar por fecha por si acaso
df = df.sort_index()
# Establecer frecuencia explícita para evitar el warning de statsmodels
df.index.freq = df.index.inferred_freq
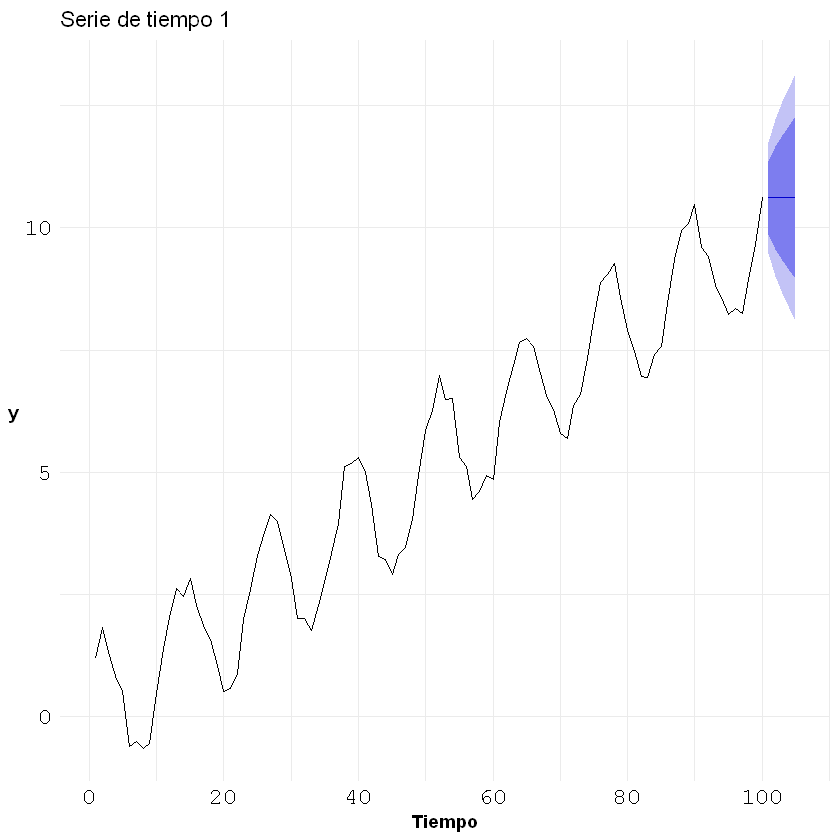
plt.figure(figsize=(18, 5))
plt.plot(df, color='navy')
plt.title("Serie de tiempo: Desempleo")
plt.xlabel("Fecha")
plt.ylabel("Valor")
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
adf_result = adfuller(df, regression='ct')
print(f'Estadístico ADF: {adf_result[0]}')
print(f'Valor p: {adf_result[1]}')
# Interpretación del resultado
alpha = 0.05
if adf_result[1] < alpha:
print("Rechazamos la hipótesis nula: La serie es estacionaria.")
else:
print("No podemos rechazar la hipótesis nula: La serie no es estacionaria.")
Estadístico ADF: -2.9263028640679423
Valor p: 0.15386331938006542
No podemos rechazar la hipótesis nula: La serie no es estacionaria.
Extracción de petróleo Ecopetrol:#
# Cargar el archivo xlsx:
df = pd.read_excel('Extracción petróleo Ecopetrol.xlsx')
# Corregir nombres de columnas si tienen espacios
df.columns = df.columns.str.strip()
# Convertir 'Fecha' a datetime y usar como índice
df['Fecha'] = pd.to_datetime(df['Fecha'])
df.set_index('Fecha', inplace=True)
# Ordenar por fecha por si acaso
df = df.sort_index()
# Establecer frecuencia explícita para evitar el warning de statsmodels
df.index.freq = df.index.inferred_freq
plt.figure(figsize=(18, 5))
plt.plot(df, color='navy')
plt.title("Serie de tiempo: Extracción de petróleo Ecopetrol")
plt.xlabel("Fecha")
plt.ylabel("Valor")
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
adf_result = adfuller(df['Serie'], regression='ct')
print(f'Estadístico ADF: {adf_result[0]}')
print(f'Valor p: {adf_result[1]}')
# Interpretación del resultado
alpha = 0.05
if adf_result[1] < alpha:
print("Rechazamos la hipótesis nula: La serie es estacionaria.")
else:
print("No podemos rechazar la hipótesis nula: La serie no es estacionaria.")

Estadístico ADF: -2.489906943558834
Valor p: 0.33302669558659626
No podemos rechazar la hipótesis nula: La serie no es estacionaria.
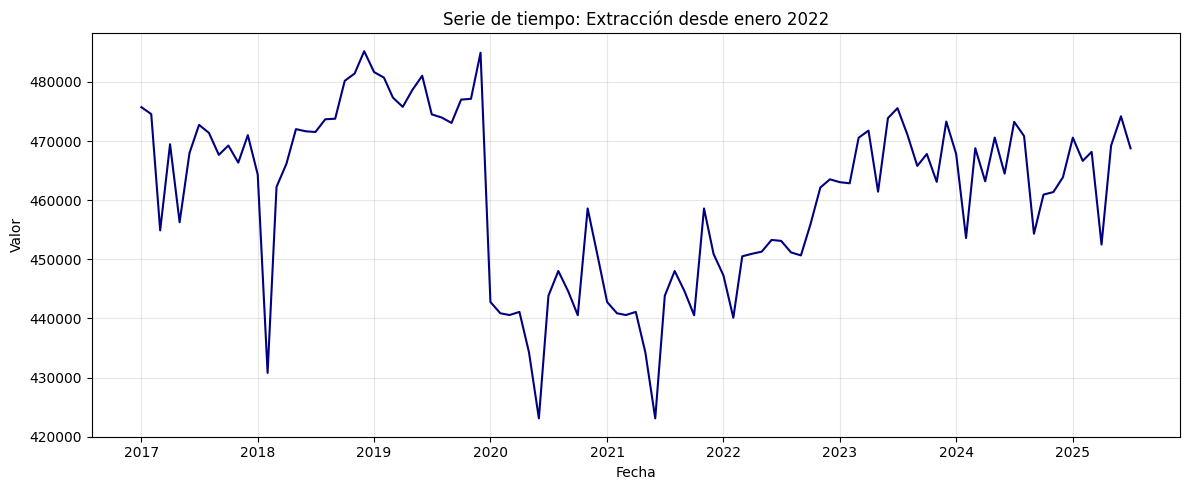
serie = df.loc['2017-01-01':]
plt.figure(figsize=(12, 5))
plt.plot(serie, color='navy')
plt.title("Serie de tiempo: Extracción desde enero 2022")
plt.xlabel("Fecha")
plt.ylabel("Valor")
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
adf_result = adfuller(serie, regression='ct')
print(f'Estadístico ADF: {adf_result[0]}')
print(f'Valor p: {adf_result[1]}')
# Interpretación del resultado
alpha = 0.05
if adf_result[1] < alpha:
print("Rechazamos la hipótesis nula: La serie es estacionaria.")
else:
print("No podemos rechazar la hipótesis nula: La serie no es estacionaria.")
Estadístico ADF: -1.8216329355610603
Valor p: 0.6942348070095631
No podemos rechazar la hipótesis nula: La serie no es estacionaria.